条形基础下格栅加筋地基的细观机理

侯 娟 徐 东 张 宸

(1.上海大学力学与工程科学学院, 上海 200444;2.School of Engineering, University of Virginia, Charlottesville, VA 22904, USA;3.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室, 武汉 430071)

条形基础下格栅加筋地基是一种较新的浅基础处理方式, 具有地基承载力高、沉降小等优点[1-3].已有的研究主要集中在采用试验手段分析格栅形式和布筋方式等对地基承载性能的影响等方面[4-6].但是土颗粒是一种离散介质, 试验手段难以直接观测筋材与土体之间的细观作用机理.结合试验现象, 部分学者基于离散元理论模拟分析了筋材与土体之间的相互作用机理[7-8].Bhandari 等[9]利用二维颗粒流软件(2D particle flow code, PFC2D) 模型研究了循环荷载作用下格栅埋深和刚度对筋土界面作用的影响, 发现浅埋时格栅的刚度对地基变形的影响较大.Han 等[10]和邱成春等[11]利用PFC2D模型研究了加筋路堤中颗粒位移与应力的变化,发现上部荷载产生的集中压应力在加筋处被均匀分散在土层上.Hou 等[12]通过PFC2D模型对水平-竖向立体加筋地基进行了数值模拟, 分析了立体加筋地基承载性能优于水平加筋地基的细观机理.Wang 等[13]通过PFC2D模型研究了格栅加筋地基内部的接触力分布, 分析了条形荷载作用下格栅加筋地基的应力分布.但是土工格栅是一种网孔结构, 而上述PFC2D模型难以进一步分析格栅网孔与土体之间的相互作用[14].鉴于此, 本工作基于模型试验[15], 建立了条形基础下纯砂与格栅加筋地基的三维颗粒流软件(3D particle flow code, PFC3D) 模型,从颗粒位移、地基中应力分布、颗粒接触力、格栅变形以及网孔效应等宏观、细观方面, 对格栅加筋地基的加固机理和破坏模式进行了研究.

1 PFC3D 模型建立

1.1 模型建立

基于已有模型试验[16-18]和数值模拟[19]研究, 本工作利用对称性, 将实际模型试验[15]取一半进行建模, 模型箱宽度为0.125 m.同时, 将条形基础一定区域外颗粒运移不明显的土体用相同刚度的墙代替, 颗粒尺寸进行适当放大, 以保证模拟计算的时效性[20].PFC3D模型采用Wall 单元模拟模型箱, Ball 单元模拟砂土, “重力沉积法” 生成砂土, 最终建立的PFC3D模型如图1 所示.

图1 PFC3D 模型Fig.1 PFC3D model

1.2 模型参数确定

PFC 模型通常采用试错法标定材料的细观参数[21], 即通过不断调整PFC 细观参数, 使得PFC 整体模拟结果与模型试验结果一致, 以此来确定PFC 模型最终采用的细观参数[18].

砂土参数通过模型试验中纯砂地基的荷载-沉降(P-s) 曲线标定.具体做法如下: 首先, 赋予砂土初始参数, 分级加载, 记录加载数据和沉降数据; 接着, 采用试错法不断调整砂土参数;最终, 使得模型试验和PFC3D模拟所得的P-s曲线较为接近, 吻合良好.PFC3D模拟和模型试验所得的纯砂地基P-s曲线如图2 所示.

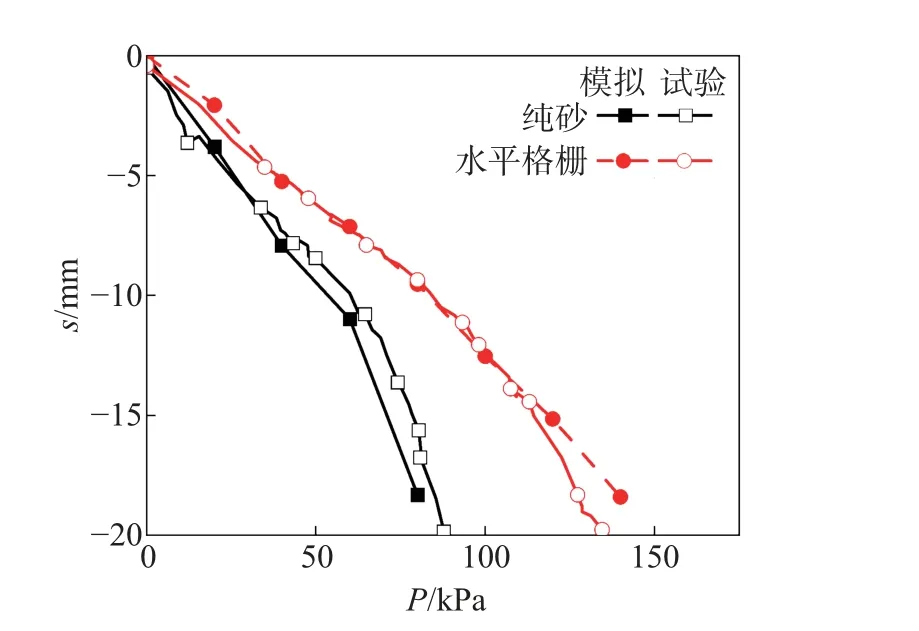
图2 不同筋材形式加筋地基的P-s 曲线Fig.2 P-s curves of reinforced foundations with different reinforcement forms

本工作对格栅进行轴向拉伸性能的数值模拟, 记录了拉伸过程中格栅的拉力-变形曲线,并与试验结果进行了对比(见图3).同时, 通过试错法不断校正, 使得最终拉伸试验和PFC3D模拟的结果趋于一致.

图3 拉伸试验与PFC3D 模拟Fig.3 Tensile test and PFC3D simulation

本工作还对格栅进行了弯曲性能的数值模拟(见图4).固定格栅最右端颗粒, 赋予格栅最左端颗粒竖直向下的力, 待受力稳定后记录最左端球颗粒的位置, 并与试验中记录的格栅颗粒位置进行对比.通过试错法不断调整, 使得最终弯曲试验和PFC3D模拟的结果趋于一致.

图4 弯曲试验与PFC3D 模拟Fig.4 Bending test and PFC3D simulation

在加筋地基数值模拟中, 设置模型箱边界的刚度和摩擦系数与砂土相同[18].同时, 采用Clump 命令生成宽度为0.075 m 的加载板来模拟条形基础, 加载板的刚度设置为砂土刚度的10 倍[22].最终, 本工作采用的PFC3D模型的细观参数如表1 所示.

表1 PFC3D 模型的细观参数Table 1 Meso parameters of PFC3D model

2 结果与分析

2.1 地基中的应力分布

图5 所示为两种地基的应力分布, 其中黑色短线表示基础初始所在位置, 基础宽度为B.由图5 可知, 无论是纯砂地基还是水平格栅加筋地基, 距离基础中心越远, 竖向压力就越小, 这与戴治恒等[23]的试验结果一致.同时, 基础边缘处的竖向压力等值线最密集, 应力扩散速度最快.这是因为竖向压力主要集中在基础正下方区域, 而在基础以外区域竖向应力值明显减小,故基础边缘正下方的竖向应力发生骤降.此外, 对比图5(a) 和(b) 可知: 纯砂地基在加载板正下方1B范围内出现应力集中现象, 潜在滑移面与地表呈一定角度向基础中心发展, 而水平格栅加筋地基未出现明显的应力集中现象; 格栅长度超过加载板正下方1.3B范围后(蓝色线表示格栅), 竖向土压力较小, 应力等值线非常稀疏.由此可初步说明, 格栅主要发挥加筋作用的长度约为1.3B ∼1.5B, 与Sharma 等[24]得到的结论一致.

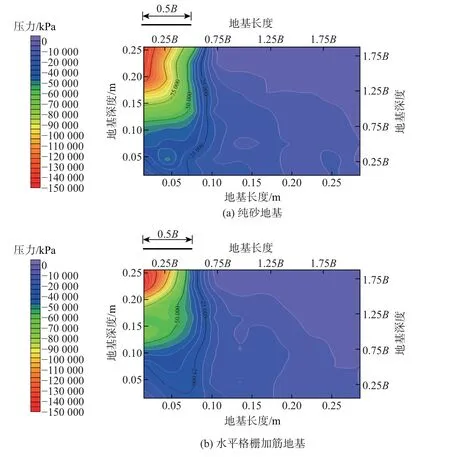
图5 不同地基中的竖向应力分布(P =120 kPa)Fig.5 Vertical stress distributions in different foundations (P =120 kPa)

2.2 土颗粒位移分析

图6 给出了纯砂地基和水平格栅加筋地基的位移矢量图.由图6(a) 可见: 在上覆条形基础荷载作用下, 纯砂地基的土体位移较大; 在加载板临近区域, 土颗粒出现明显的水平和竖向运动, 基础沉降和砂土地表的隆起较大, 在土体内形成了明显的滑移面(红色实线).相反地, 由图6(b) 可见: 水平格栅加筋地基土体的位移和地表隆起远小于纯砂地基, 且滑移面并不明显.观察筋材附近的放大区域A(见图6(c)) 发现: 部分砂土穿过格栅的网孔后运动减缓(紫色实线框); 部分颗粒由于格栅纵横肋的作用, 在格栅上下左右的移动均受到明显的限制(黄色实线框), 进而使得水平格栅加筋地基砂土的整体位移小于纯砂地基.观察格栅网孔内的土颗粒(见图6(d)) 可见: 格栅的网孔结构通过嵌固作用(紫色和黄色框) 提高了筋土之间的相互作用; 格栅对土颗粒竖直和水平向位移的限制可以有效减缓土颗粒向右和向上形成连续的滑移破裂面,使得颗粒与格栅协同作用形成一个整体, 进而提高格栅加筋地基的承载性能, 减小地基变形.由此可知: 格栅约束土体后, 筋土之间的细观变化是格栅加筋地基宏观承载性能发生改变的根本原因.

图6 不同地基的位移分布Fig.6 Displacement distributions of different foundations

2.3 土颗粒接触力分析

图7 为两种不同地基砂土颗粒的接触力分布图.由图7(a) 可知, 纯砂地基中的砂土压力主要集中在基础正下方, 并且距离加载板中心越远, 接触力分布越分散.由图7(b) 可知, 与纯砂地基相比, 格栅可以明显减小和均化地基中土颗粒之间的接触力, 力链较纯砂地基细, 分布也更加均匀.由图7(c) 可知, 纯砂地基的力链较粗且从上到下贯通区域比较明显, 即力链向基础外偏转较小, 应力集中在加载板临近区域.由图7(d) 可知: 对于格栅加筋地基, 基底的接触力链呈柱状穿过格栅网孔; 水平格栅加筋地基的力链在穿过格栅后趋于发散, 力链方向有所改变(绿色箭头), 即力链进行了重分布并趋于均匀.这说明格栅的嵌固作用可以有效均化砂土颗粒中较集中的接触力, 使得条形基础下的集中应力向较大范围进行传递和扩散.该应力重分布和扩散作用进一步提高了格栅加筋地基的承载性能.

图7 不同地基的接触力Fig.7 Contact force of different foundations

2.4 格栅位移分析

图8 给出了格栅的位移矢量图, 其中黄色虚线框为加载板的位置.由图8(a) 可知, 横肋的水平位移比纵肋明显, 在基底1.5B范围内的横肋位移(1、2、3 号横肋) 尤为显著.由图8(b)可知, 在基底范围外的区域, 格栅纵肋颗粒的位移有向左运动的趋势(绿色箭头).这可能是因为纵肋虽然受拉力后总长有所增加, 但由于格栅的变形是由土体的挤压造成的, 因此荷载作用下地基产生变形, 使得加筋垫层由平面变成曲面, 进而使得水平格栅距离变短.此外, 格栅弯曲后, 抗拉强度进一步得到了发挥, 增强了格栅对土体的被动阻力和约束作用.由图8(b) 还可以看出: 在基础中心线1.5B范围内, 格栅的位移整体向下; 超过1.5B后, 格栅的位移整体向上; 离基底中心0.75B处格栅变形出现反弯点(红色箭头), 格栅对反弯点左侧的土体产生向上的作用力, 对反弯点右侧的土体产生向下的作用力, 即格栅呈现出较好的张拉膜效应, 从而调节了地基的不均匀沉降, 提高了整体格栅加筋地基的承载性能, 这也很好地解释了图5 中格栅能均化地基中整体应力分布的现象; 基础正下方的格栅变形较大; 随着远离基础中心, 格栅的变形逐渐减小; 反弯点以外的格栅变形远小于反弯曲点以内的.结合图5 的应力分布特征可知, 格栅主要发挥加筋作用的长度约为1.3B ∼1.5B.

图8 格栅的位移Fig.8 Displacements of geogrids

2.5 格栅的接触力分析

图9 所示为水平格栅受力变形后的接触力分布图.可以明显看出, 加载板正下方格栅的拉力远大于加载板以外格栅的拉力, 并且格栅的拉力随着离加载板中心距离的增大而逐渐减小.这与图3 中砂土颗粒的压应力分布规律一致.

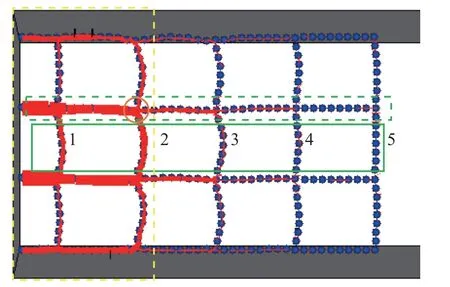
图9 格栅的接触力Fig.9 Contact force of geogrids

为了分析格栅之间的法向接触力分布,通过c_nforce 和b_clist 命令提取中间横肋(图9 中绿色实线框内的1∼5 号横肋) 的法向接触力, 绘制了格栅横肋沿模型箱宽度方向的法向接触力分布(见图10).可以看出: 1 号和2 号横肋法向接触力较大, 其中2 号最大, 原因是2 号横肋在基础边缘临近正下方位置处, 其附近的砂土既有向下运动的趋势, 也有向右运动的趋势,因此砂土颗粒对格栅的挤出效应更明显; 3∼5 号横肋随着离加载板距离的逐渐变大, 其法向接触力则逐渐减小; 超过3 号横肋后, 4 号、5 号横肋的变形不再明显.

图10 格栅横肋的法向接触力Fig.10 Normal contact force of transverse ribs of geogrids

同理可提取格栅纵肋上的法向接触力(图7 绿色虚线框).本工作以墙体与格栅接触点为原点, 模型箱长度方向为横坐标, 纵肋法向接触力为纵坐标, 绘制了格栅沿模型箱长度方向的法向接触力分布(见图11).可以看出: 格栅沿纵肋上的法向接触力呈阶梯状分布; 两根横肋之间的纵肋颗粒法向接触力相差不大, 在纵肋与横肋交点处的筋材法向接触力发生突变.这与Wang[22]用离散元分析得出的结论基本吻合.此外, 由图10 和11 可知: 格栅纵肋、横肋接触力较高的区域在距离基础正下方中心线0.75B范围内.结合图5(b) 可知, 格栅长度超过基础正下方1.3B范围后, 应力等值线非常稀疏.因此, 格栅能够有效发挥加筋作用的范围约为1.3B ∼1.5B.

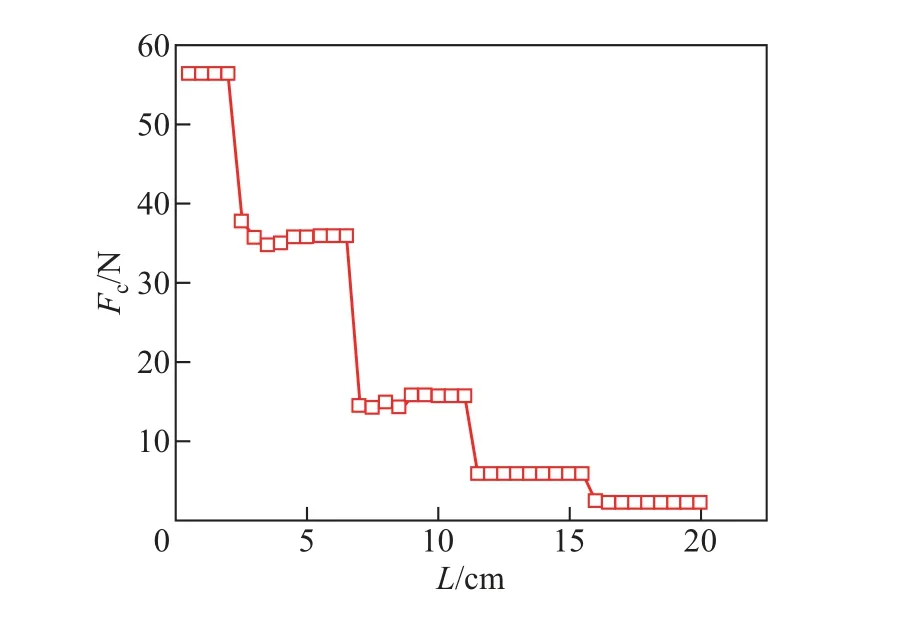
图11 格栅纵肋的法向接触力Fig.11 Normal contact force of longitudinal ribs of geogrids

图12 所示为水平格栅节点(图7 中橙色圆圈) 受力图, 其中3 号球体为节点颗粒; 1 号、2 号、4 号球体为纵肋筋材颗粒; 5 号、6 号球体为横肋筋材颗粒;fi表示筋材第i号球体受到的土体摩擦力在y轴的投影;和表示第i号筋材球体对第j号筋材球体的法向接触力和切向接触力.

图12 水平格栅节点受力示意图Fig.12 Stress diagram of horizontal geogrids

对2 号球体列y轴方向的平衡方程为

式中: 接触力=13.5 N,=14.6 N, 因此,f2=0.9 N.

对3 号球体列y轴方向的平衡方程为

式中:fn43=36 N,fn23=14.6 N,fs53=8.0 N,fs63=9.4 N, 因此,f3=3.9 N.

对比摩擦力f2和横肋阻挡力f3可知, 格栅横肋的阻挡力远大于筋土之间的摩擦力.这与Moraci 等[25]的结论一致.横肋对纵肋拉力提高的贡献占比为82%, 而筋土摩擦力的贡献占比仅为18%.这进一步说明格栅横肋对土体产生阻挡力, 并通过节点传递给纵肋, 导致纵肋拉力提高, 张拉膜效应增大, 格栅对土体侧限作用增强, 进而提高了整体格栅加筋地基的承载性能.

3 结论与展望

本工作通过PFC3D软件, 建立了条形基础下不同地基的颗粒流模型.通过对比分析竖向应力、颗粒位移和接触力分布等, 从细观角度阐明了格栅加筋地基的加固机理, 得到如下主要结论.

(1) PFC3D模拟的应力-沉降曲线与试验数据吻合良好.在条形基础下, 水平格栅加筋地基的承载性能明显优于纯砂地基, 格栅主要发挥加筋作用的长度约为1.3B∼1.5B.在格栅主要发挥加筋作用的长度内, 格栅能较好地均化地基中的应力.

(2) 在格栅网孔的嵌固作用下, 土颗粒在格栅网孔上下左右的移动均受到明显的限制, 使得砂土的相对位移较小, 筋土整体性增强, 从而提高了整体格栅加筋地基的承载性能.

(3) 筋土之间的摩擦力对格栅纵肋的拉力影响较小, 但格栅横肋会对土体产生明显的阻挡力, 并通过节点传递给纵肋, 进而使得纵肋的拉力得到充分发挥.同时, 格栅变形存在一个反弯点, 格栅对反弯点一侧的土体产生向上的作用力, 对反弯点另一侧的土体产生向下的作用力, 格栅呈现出了较好的张拉膜效应, 进而调节了地基的不均匀沉降, 改善了格栅加筋地基的承载性能.

本工作仅分析了单层水平格栅加筋地基的细观机理, 但同时格栅的层数和布筋方式等也对加筋地基承载性能具有重要的影响.后续应开展不同格栅层数和不同布筋方式下格栅加筋地基的细观加固机理研究, 以系统地表征条形基础下格栅加筋地基的承载性能和加固机理.