床面形态渗透率对潜流交换特性的影响

赵 亮 王学勇 王岱峰 樊靖郁

(1.上海大学力学与工程科学学院, 上海 200444;2.上海大学上海市应用数学和力学研究所, 上海 200072)

潜流交换是河流水环境系统中, 各种物质(水、溶质、污染物、胶体和细颗粒等) 在与地表水相邻的饱和沉积物层(潜流带) 中发生的一种重要对流过程[1-3].潜流交换对潜流带中溶解氧、氮/磷营养盐、重金属、有机污染物以及胶体、细颗粒物(如微塑料) 的迁移转化和通量演变起控制和调节作用[4-5], 影响潜流带的生物地球化学特征[6-8]对河流生态系统的健康维持和功能发挥起着非常重要的作用[4,9].

潜流交换可由不同尺度和类型的水静力/水动力因子驱动, 在河道局部尺度上各种类型的床面形态是潜流交换的重要驱动因子[10-11].上覆水流与床面形态的相互作用会使床面压力变化不均匀, 驱动上覆水及其所携带的各种物质产生进出底床的潜流交换[1,10].床面形态驱动的潜流交换涉及到众多影响因素.已有研究表明, 水动力作用(流量或流速/水深、非恒定性)、床沙组成和床面形态物理特性(渗透率、孔隙度和非均质性) 对潜流交换的通量、潜流路径和停留时间的分布具有重要影响[12-14].

非均质底床结构在天然河流中是普遍存在的.近年来河床的非均质性在不同的时空尺度上对潜流交换的影响日益受到关注[15-17], 如不同粒径床沙组成底床[18]、分层底床[19]以及低渗透率透镜体[20]等.对于存在床面形态的潜流交换, 本工作侧重于考虑河道局部尺度上的非均质性、自然或人工形成的床面形态组成单元, 由于其物理特性与其下底床往往存在明显差异,如砂质河道中自然存在的倒伏树木[21]、肋状/簇状砾石堆积体[11]等障碍物, 人工构建的圆木坝(坎、堰)[22]、阶梯-深潭[23]等潜流型河床结构, 因此这些床面形态组成单元的物理特性(如渗透率、孔隙度) 与底床泥沙相比呈现出河道局部尺度上的空间变化.即使对于存在床面形态(如沙波) 的均质底床结构, 由于上覆水体中细颗粒泥沙的局部沉积作用[24], 或床面形态泥沙颗粒表面生物膜生长形成的生物堵塞效应[25], 故床面形态组成单元的渗透率会明显改变, 形成空间渗透率强烈不连续变化的非均质底床结构.对于这种类型的非均质底床结构, 床面形态渗透率的变化对近底区域上覆水/孔隙水耦合流动结构具有显著的影响[26], 在与之相关的潜流交换特性方面, 目前较少有学者研究床面形态组成单元渗透率的相对变化对潜流交换通量所带来的定量差异, 因此床面形态组成单元的物理特性(如渗透率、孔隙度) 对潜流交换特性的影响规律尚待深入研究[27-28].

本工作通过实验室环形水槽实验, 采用概化的2 维离散床面形态, 主要研究存在床面形态砂质底床条件下, 床面形态组成单元与底床渗透率的相对变化与潜流交换通量之间的定量关联和变化特征, 并采用参数化方法分析床面形态组成单元的物理特性(渗透率变化) 对有效扩散系数的影响趋势.

1 实验装置和测量方法

1.1 实验装置

本实验在上海大学力学所自行研发的环形水槽中进行[28-29], 实验装置如图1 所示.环形水槽由有机玻璃制成的内、外径不同的环形槽道, 以及剪力环、操作台、电机、减速机、底座等构成, 槽道内、外径分别为0.6 和1.0 m, 槽道宽度为0.2 m, 高度为0.4 m, 有效体积约为0.7 m3.电机驱动安装于水槽上部的剪力环转动, 带动水体表面产生单向流动.通过调节剪力环的转速(R) 可以控制上覆水的平均流速(U).

图1 环形水槽示意图Fig.1 Schematic diagram of an annular flume

在实验过程中剪力环转速控制在低速范围(R≤20 r/min), 以避免底床泥沙的再悬浮, 同时可近似忽略水槽内形成的2 次流.每个实验工况上覆水的水深(H= 15.0 cm) 和体积(Vw)均保持不变.与循环直水槽相比, 环形水槽的优点在于把直槽长度转化为时间尺度, 可模拟断面水流状态相同的无限长的明渠水流, 同时无需回水系统和消能措施, 结构简单且易于操作.此外, 环形水槽上覆水体积与底床泥沙体积(Vs) 之比可方便调节, 在实验过程中上覆水溶质的浓度变化范围相对较大, 可有效提高上覆水溶质浓度的测量精度.

1.2 测量方法

实验底床泥沙按粒径(dg) 大小分为3 种: 细沙、中沙和粗沙.3 种泥沙样品采用粒径较为均匀(粒径分布范围较窄) 的模型沙(石英砂), 通过筛分法测量3 种泥沙的粒径分别为细沙(dg= 0.425 mm)、中沙(dg= 0.950 mm) 和粗沙(dg= 2.000 mm).通过水蒸发法对泥沙样品的孔隙度进行测定, 结果分别为0.42(细沙)、0.44(中沙) 和0.45(粗沙), 渗透率(K) 可根据Kozeny-Carmen 公式估算[1,29], 相应的渗透率值分别为2.21×10-6cm2(细沙)、1.36×10-5cm2(中沙) 和6.69×10-5cm2(粗沙)[29].在实验过程中, 将15 cm 厚的模型沙(分别采用中沙和粗沙) 均匀铺设在水槽底部构成平整底床, 底床泥沙厚度(db)、底床表面积(As) 和体积(Vs=Asdb) 均保持不变.床面形态采用概化的2 维离散床面形态, 包括人工构建的具有不同渗透率的方形2 维离散床面形态和人工铺设的沙波床面形态, 其几何特征分别如图2 和3 所示.由不同渗透率床面形态组成单元的高度(h= 2.0 cm) 保持相同, 通过其间距(w) 的变化将不同数量的沙袋或沙波均匀排列在水槽底床表面来实现(3 ≤w/h≤11).

图2 方形2 维离散床面形态示意图Fig.2 Schematic diagram of square two-dimensional discrete bedform

图3 沙波床面形态示意图Fig.3 Schematic diagram of sand wave bedform

采用非吸附性氯化钠(NaCl) 作为代表性溶质(上覆水中分子扩散系数为Dm).实验开始时, 待水槽启动稳定运行一段时间后, 将配制的高浓度NaCl 溶液添加于上覆水中(底床孔隙水初始浓度为0), 混合均匀后的上覆水溶质浓度作为初始浓度(C0), 通过虹吸采样和测量得到上覆水NaCl 浓度随时间(t) 的变化(C(t)), 即可确定不同工况的潜流交换通量(J)[28].在实验过程中, 为避免上部剪力环转动对采样的扰动, 采样点设置于中间水深位置(见图1), 测量结果表明此区域上覆水溶质浓度的垂向分布较为均匀.为便于比较, 本实验不同工况的上覆水溶质浓度C(t) 的实验数据由量纲一变量C∗(C∗=C/C0) 的时间序列给出.有效扩散系数的分析采用Deff/D′m量纲一形式, 其中D′m(D′m=Dm/(1+3(1+θ))) 为孔隙水中NaCl 分子扩散系数.根据上覆水量纲一溶质浓度C∗∼t1/2曲线的初始斜率S(S= dC∗/dt1/2), 即可定量确定有效扩散系数Deff= π(VwS/(2Asθ))2, 由实验数据拟合得到[29].每个实验工况上覆水初始浓度(C0=0.05 mol/L) 和采样历时(180 min) 均保持相同.

1.3 实验工况

本实验通过改变床面形态构成单元以及底床泥沙组成来实现渗透率的相对变化.本实验共设置了30 组实验工况, 其中平整底床分别由中沙和粗沙构成, 存在床面形态的实验工况则相应设置了不可渗透(亚克力棒)、可渗透2 维离散床面形态(由纱布包裹不同粒径泥沙制备的细长条沙袋) 和沙波(由粗沙人工铺设), 以改变床面形态组成单元的渗透率.实验参数和工况如表1 所示.

表1 实验参数和工况Table 1 Experimental parameters and runs

2 结果和分析

2.1 底床渗透率变化对潜流交换特性的影响

床面形态驱动的潜流交换不仅与水动力作用(如流量或流速/水深、非恒定性和近底紊动特性) 有关, 而且还涉及到底床和床面形态的物理特性(如渗透率、孔隙度).以往研究结果表明, 对于可渗透的砂质或砾石底床, 床沙组成对潜流交换通量影响较大, 在床面附近区域上覆水流与床面形态的相互作用将会驱动各种物质产生进出底床的泵吸交换[1,28].与以往均质底床条件下的相关水槽实验相比, 本工作侧重于当定量分析床面形态和底床的物理特性存在差异时, 即非均质底床结构条件下的潜流交换特性, 因此为对比需要也设置了相应的均质底床结构实验工况, 包括平整和存在床面形态这2 种情况.

图4 给出了在上覆水平均流速U= 10.6 cm/s、中沙和粗沙平整均质底床条件下(工况1和2), 上覆水量纲一溶质浓度C∗随时间t的变化.

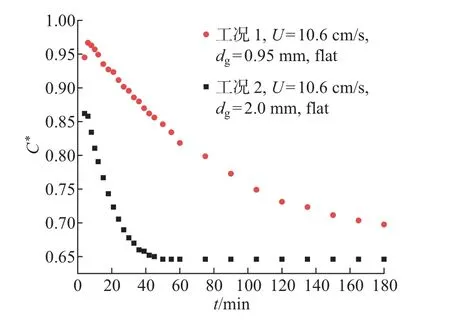
图4 中沙和粗沙平整底床条件下上覆水浓度随时间的变化Fig.4 Variation of overlying water concentration with time under the conditions of flat beds with medium and coarse sands

由图4 可见, 对于平整均质底床, 在初始交换阶段粗沙平整底床条件下的上覆水溶质浓度C∗曲线下降速度明显快于中沙平整底床情形, 即工况2 在t= 50 min 左右就已达到交换平衡, 而工况1 在采样过程结束时仍未达到交换平衡.由图4 中C∗曲线初始斜率S确定的量纲一有效扩散系数Deff/D′m, 工况2 所得结果为Deff/D′m=1.89×104, 与工况1 所得结果(Deff/D′m= 1.90×103) 相比, 其增幅为894.7%, 表明随底床渗透率的增大, 潜流交换通量和有效扩散系数有明显增大.

图5 给出了在上覆水平均流速U=10.6 cm/s, 存在可渗透2 维离散床面形态中沙和粗沙底床条件下(w/h=3, 6, 8, 11), 上覆水量纲一溶质浓度C∗随时间t的变化.

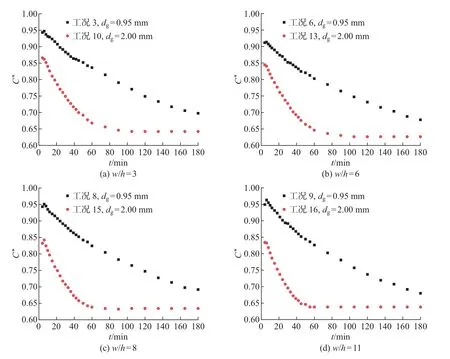
图5 中沙和粗沙底床条件下(存在可渗透2 维离散床面形态) 上覆水浓度随时间的变化Fig.5 Variation of overlying water concentration with time under the conditions of medium and coarse sand beds in the presence of permeable 2D discrete bedform

由图5 可见, 当存在相同渗透率的2 维离散床面形态时, 底床渗透率变化对潜流交换通量的影响趋势总体上类似于平整床面情形, 对于较高渗透率的粗沙底床, 其潜流交换通量明显大于较低渗透率的中沙底床情形, 这说明底床渗透率的增大对潜流交换(包括湍流渗透和泵吸交换) 起促进作用.在非均质粗沙底床条件下的潜流交换通量随底床渗透率的变化, 与均质中沙底床条件下的实验结果相比, 各工况的增幅并不完全相同.比较分析w/h变化范围(3 ≤w/h≤11) 内, 各相应工况的量纲一有效扩散系数Deff/D′m定量数据.w/h= 3 时工况10 所得结果(Deff/D′m= 1.41×104) 相比工况3 (Deff/D′m= 2.39×103) 增幅为490.0%;w/h=6 时工况13 所得结果(Deff/D′m=1.82×104) 相比工况6 (Deff/D′m=3.94×103) 增幅为361.9%;w/h= 8 时工况15 所得结果(Deff/D′m= 1.96×104) 相比工况8 (Deff/D′m=2.39×103) 增幅为720.1%;w/h=11 时工况16 所得结果(Deff/D′m=2.11×104) 相比工况9 (Deff/D′m=2.12×103) 增幅为895.3%.由此可见, 非均质粗沙底床条件下的有效扩散系数与均质中沙底床条件下所得结果相比, 其增幅总体上要低于平整均质底床情形.可见, 对非均质底床结构而言, 在w/h变化范围(3 ≤w/h≤11) 内, 底床和床面形态组成单元的渗透率变化均会对潜流交换通量和有效扩散系数产生不同程度的影响.随着底床和床面形态组成单元渗透率的增大, 底床表面和床面形态组成的单元内部的湍流渗透相应增强, 使得潜流交换作用得以增强.同时, 床面形态驱动的潜流交换还受到床面形态几何特征(w/h) 的影响, 非均质粗沙底床条件下的有效扩散系数随w/h的增大并不完全呈单调变化.

2.2 床面形态渗透率变化对潜流交换特性的影响

为进一步分析当床面形态组成单元的渗透率与底床存在差异时, 这种局部尺度上的非均质性对潜流交换通量的定量影响, 本工作利用粗沙底床条件下不同渗透率床面形态组成单元的各实验工况所得数据, 比较分析床面形态组成单元渗透率变化对潜流交换特性的影响.

图6 给出了在粗沙底床条件下(w/h=3, 6, 8, 11), 存在不可渗透、可渗透2 维离散床面形态和沙波各实验工况, 上覆水量纲一溶质浓度C∗随时间t的变化.

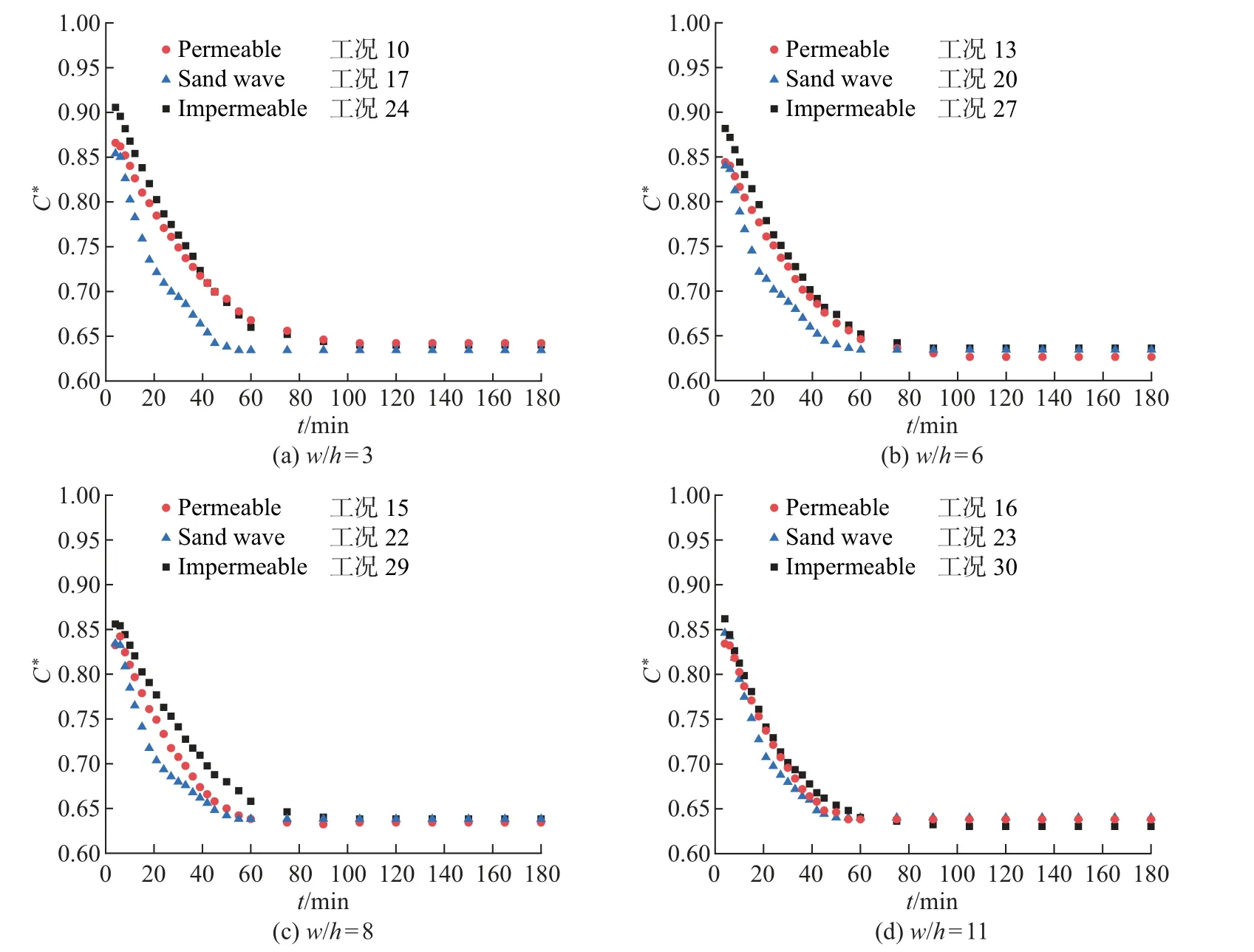
图6 粗沙底床条件下(存在不同渗透率床面形态) 上覆水浓度随时间的变化Fig.6 Variation of overlying water concentration with time under the conditions of coarse sand beds in the presence of the bedforms with different permeabilities

由图6 可见, 对于相同渗透率的粗沙底床随床面形态组成单元渗透率的变化, 潜流交换通量呈较为一致的变化趋势, 即随着床面形态组成单元渗透率的降低, 初始交换阶段上覆水溶质浓度C∗随时间的推移下降较缓, 达到最终交换平衡的时间相对变长, 相应潜流交换通量逐渐减小.由分析w/h变化范围(3 ≤w/h≤11) 内各相应工况的量纲一有效扩散系数Deff/D′m定量数据可知, 虽然床面形态组成单元渗透率的变化对潜流交换通量的影响程度不如底床渗透率的变化, 但对有效扩散系数仍存在不可忽视的影响.w/h= 3 时工况10 所得结果(Deff/D′m= 1.41×104) 相比工况17 (Deff/D′m= 2.05×104) 降低了31.2%,工况24 所得结果(Deff/D′m= 7.95×103) 则降低了61.2%;w/h= 6 时工况13 所得结果(Deff/D′m=1.82×104)相比工况20(Deff/D′m=2.26×104)降低了19.5%,工况27 所得结果(Deff/D′m=1.24×104)则降低了45.1%;w/h=8 时工况15 所得结果(Deff/D′m=1.96×104)相比工况22(Deff/D′m=2.36×104)降低了16.9%, 工况29 所得结果(Deff/D′m=1.42×104)则降低了39.8%;w/h= 11 时工况16 所得结果(Deff/D′m= 2.11×104) 相比工况23(Deff/D′m= 2.19×104) 降低了3.7%, 工况30 所得结果(Deff/D′m= 1.70×104) 则降低了22.4%.上述分析表明, 床面形态组成单元渗透率相对较低的非均质底床结构(存在不可渗透、可渗透2 维离散床面形态) 与均质底床结构(存在沙波床面形态) 相比, 潜流交换趋于减弱.

2.3 水动力影响机理分析

一般而言, 床面形态驱动的潜流交换受到多种物理驱动机制的共同作用, 包括分子扩散、剪切离散、湍流渗透和泵吸交换等[29-30].对于具有一定渗透率的砂质底床, 泵吸交换和湍流渗透是影响潜流交换特性的主要驱动机制, 而有效扩散系数综合反映了多种物理机制的共同作用.根据不同实验工况得到的量纲一有效扩散系数, 不仅可定量分析床面形态组成单元的渗透率变化对有效扩散系数的影响, 同时还可对比分析均质和非均质底床结构条件下的潜流交换水动力影响机理.图7 给出了不同实验工况下的量纲一有效扩散系数Deff/D′m柱状图, 图中M 表示为中沙底床, C 表示为粗沙底床, 2 条虚线分别表示中沙和粗沙在平整底床条件下的Deff/D′m值.

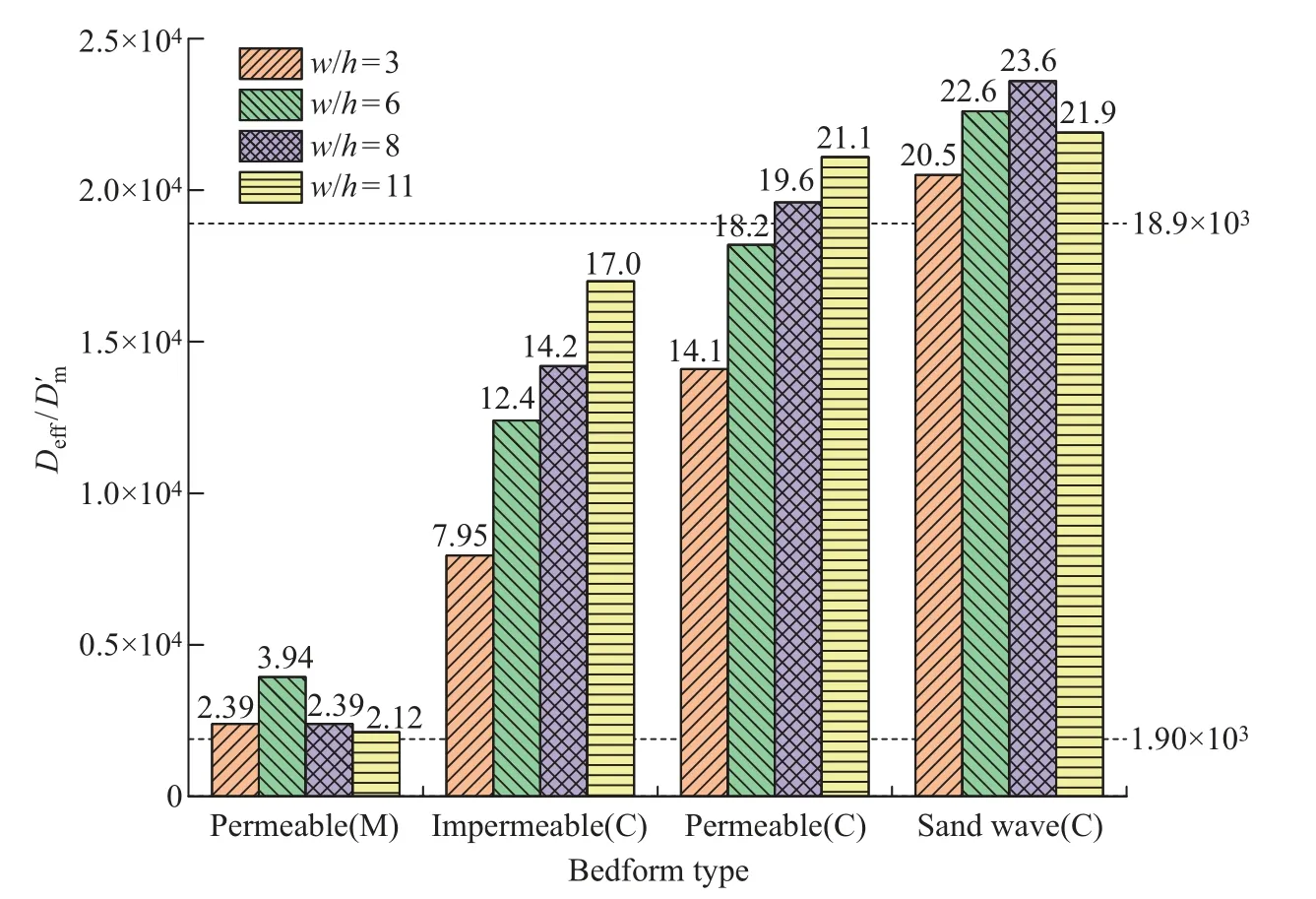
图7 各工况有效扩散系数柱状图Fig.7 Histogram of effective diffusion coefficients for all experimental runs

由图7 可见, 对于存在床面形态的均质底床结构(包括中沙底床和沙波床面形态对应工况), 在w/h变化范围(3 ≤w/h≤11) 内与平整底床相比, 其有效扩散系数均有不同程度的增大, 说明对于存在床面形态的均质底床结构来说, 床面形态的存在引入了附加的泵吸交换, 潜流交换受到湍流渗透和泵吸交换的共同作用, 其有效扩散系数相比平整底床情形总体上得以增大.从分析均质底床结构条件下各工况的Deff/D′m定量数据可知, 与相应的平整底床相比,存在床面形态的中沙底床典型工况(w/h=6) 的Deff/D′m增幅为107.4%, 粗沙底床典型工况(w/h= 8) 的Deff/D′m增幅为24.9%, 这也说明了泵吸交换对潜流交换的相对贡献随床沙渗透率的增大趋于减弱, 湍流渗透的相对贡献趋于增强.

对于存在床面形态的非均质底床结构(粗沙底床对应工况), 随着床面形态组成单元渗透率的降低, 各工况有效扩散系数总体上趋于减小(见图7).对比分析存在不可渗透、可渗透床面形态组成单元各工况的Deff/D′m定量数据, 与平整底床相比其有效扩散系数呈现不一致的变化趋势, 即不可渗透床面形态对应工况在w/h变化范围(3 ≤w/h≤11) 内, 其有效扩散系数均小于平整底床所得结果.而可渗透床面形态对应工况在床面形态组成单元相对稀疏时(w/h= 8, 11), 其有效扩散系数大于平整底床的Deff/D′m值; 当床面形态组成单元相对密集时(w/h= 3, 6), 其有效扩散系数小于平整底床Deff/D′m值.上述情况说明, 在非均质底床结构条件下, 湍流渗透和泵吸交换对潜流交换通量的相对贡献不仅与底床渗透率有关, 同时还受到床面形态组成单元渗透率变化的影响.具体来看, 对于存在不可渗透床面形态典型工况(w/h=8), 其有效扩散系数Deff/D′m(1.42×104) 相比平整底床(1.89×104) 降低了24.9%, 其原因在于①不可渗透床面形态组成单元遮挡了部分底床面积, 使得上覆水/孔隙水物质交换表面积减小, 减弱了湍流渗透; ②存在不可渗透床面形态典型工况的有效扩散系数Deff/D′m相比沙波工况(w/h=8) 降低了39.8%, 其降幅大于平整底床情形, 由此可知泵吸交换也有一定程度的减弱.

综合来看, 对于床面形态与底床渗透率存在差异的非均质底床结构, 床面形态组成单元渗透率的减小对潜流交换起抑制作用, 尤其对于存在不可渗透床面形态非均质底床结构, 与均质底床结构(平整或存在床面形态) 相比, 湍流渗透和泵吸交换均趋于减弱, 相应地有效扩散系数总体上呈不同程度的减小趋势.

3 结束语

通过实验室环形水槽实验, 采用概化的2 维离散床面形态, 测量得到床面形态组成单元渗透率与潜流交换通量之间的定量关联和变化特征, 对比分析了床面形态组成单元的渗透率变化对有效扩散系数的影响.实验结果表明, 对于床面形态与底床渗透率存在差异的非均质底床结构来说, 床面形态组成单元的渗透率变化对潜流交换起着不可忽视的作用.在本实验参数变化范围内, 床面形态的存在引入了附加的泵吸交换, 泵吸交换对潜流交换通量的相对贡献与床面形态组成单元的渗透率变化密切相关.随着床面形态组成单元渗透率的降低, 底床表面和床面形态组成单元内部的湍流渗透作用趋于减弱, 同时床面形态诱导的泵吸交换受到一定程度的抑制, 与平整均质底床相比有效扩散系数总体上呈不同程度的减小趋势.