鞣制过程中皮革在转鼓内的形变特征及受力分析

韩明真，江卓成，谢果，曾运航，王亚楠＊

（1.四川大学制革清洁技术国家工程实验室，四川 成都 610065；2.四川大学轻工科学与工程学院，四川 成都 610065；3.四川大学水利水电学院，四川 成都 610065）

制革80%以上的加工过程（包括准备工段、鞣制工段和湿整饰工段）是在水介质中通过转鼓设备来完成。以制革的核心过程——鞣制为例，它可被看作是在转鼓的机械作用下，水相中的鞣剂分子扩散进入三维皮革纤维网络并进行化学交联反应的过程[1-2]。鉴于皮革纤维网络多层级结构的复杂性，皮革的鞣制效果与鞣剂在纤维网络中的传质特性密切相关[3-5]。因此，研究皮革在转鼓中的运动特征和动力学规律，从设备和工艺角度增强传质效果，有助于提高成革质量，并实现节能、增效、减排等目标。

皮革是一种多孔柔性物体，其在转鼓内的运动会引起内部孔隙的挤压形变，促进化学品在皮革内部的传递。针对类似的加工过程，有学者调研了不同转鼓结构对加工效果的影响，以探寻可实现更高效加工的转鼓结构改进方法。例如Jiang 等[6]基于数值模拟仿真分析了转鼓内不同挡板数量和布置形式对颗粒物混合的影响，发现挡板呈中心对称布置且数量为4 和6 时，转鼓具有最好的加工效果。Chand 等[7]等通过数值模拟仿真对比了长转鼓和短转鼓内物料的混合情况，结果表明短转鼓内端板对物料存在较强的摩擦作用，更有利于物料混合，其内部物料在加工过程中彼此分离的程度可降低13%以上。Yu 等[8]提出了一种具有交错挡板的转鼓结构，该设计中将长度不等的挡板布置于转鼓内部，计算数据表明该转鼓比传统均匀布置挡板的转鼓具有更好的物料混合效果，其内部物料的混合系数可提升100%以上。然而皮革是一种连续且不具有特定形貌的柔性物体，其在转鼓内运动时具有非常复杂的形变特征，针对该特点进行转鼓结构的改进难度大，对应的研究报道也较少，此类转鼓结构优化改进方案有待进一步研究。

据此，可通过对转鼓内皮革的形变和受力过程进行研究，定量获取有利于皮革内部化学品传递的形变参数，从而为后续制革转鼓的结构优化提供理论依据。虽然目前尚未有皮革形变和受力的相关研究报道，但已有学者通过实验和模拟方法对类似柔性物体进行了相关研究，其研发方法可为本文研究提供参考。龚肖等[9]提出了一种基于空间和时间序列重构获取柔性物体三维运动特征的方法，采用具有圆斑点的柔性布料进行实验验证，结果表明该方法的计算误差可小于1%。薛冕等[10]采用改进光流法对连续运动的柔性面料图像数据进行了分析，得到了6 个不同位置处的瞬时速度和加速度数据，通过对比分析表明改进方法可使数据误差减小约38%。廖芳等[11]针对点状特征柔性物体提出了一种改进的三维运动捕获方法，基于人脸表情的案例分析验证了改进方法的可靠性，结果表明该改进方法比sift算法具有更高的捕获精度。Patel 等[12]针对三维柔性复合纤维材料构建了受力和运动的仿真计算模型，分析了该类柔性物体的形变和失效特性，并通过实验验证了分析结果的可靠性。Wang 等[13]通过实验和模拟的方法分析了三维柔性物体的受力和褶皱特征，据此提出了一种通过表面强化提高柔性物体使用寿命的方法，研究表明该方法可使柔性物体发生最大形变处的剪切角从66.5°降低至55.1°。万文章等[14]提出了一种基于蜂窝状多孔结构假设的形变计算模型，采用该模型可对柔性物体的瞬时形变过程进行预测，可获取400 dpi 以上的可视化图像预测结果。此外，在前期研究中基于可视化图形数据和二值化处理分析了皮革在转鼓内的运动特征，获取了在特定条件下有利于皮革加工的转鼓转速范围[15]。然而前期实验数据无法明确指出适合皮革加工的受力条件，当实验转鼓与工业转鼓尺寸差异较大时，相关数据对实际生产的指导意义有限，涉及到转鼓尺寸、推力和形变三者之间的理论关系有待进一步研究。

本研究拟基于转鼓内皮革的典型运动和形变特征，构建简化的动力学分析模型，以进一步探究有利于皮革加工的转鼓动力学参数。首先根据可视化实验观测图像，分析典型的皮革运动和形变特征，提出可描述皮革运动规律的简化解析几何模型，随后建立皮革在转鼓内的受力分析理论计算模型，最后结合可视化实验数据，验证理论模型的准确性。该模型可用于对不同情况下皮革的形变和受力数据进行分析，获取对应的转鼓优化操控方案，对未来智能制革的参数优化具有指导作用。

1 理论计算模型

皮革作为柔性物体，在转鼓设备中的形变可近似看作一个二维物体的周期性形变过程，该过程的图像及简化模型如图1 所示。具体而言，皮革会经历由圆形到椭圆形再到圆形的形变。当皮革先向上运动，随后在转鼓内沿着壁面向下滑动时，会受到周期性机械作用力，这些力是由转鼓内的机械构件施加的。当机械构件对皮革作用时，皮革沿转动方向发生挤压形变，整体处于压缩状态，从而使得皮革在轴向二维切面上的形状类似于圆形；当机械构件离开皮革后，周期性作用力消失，皮革的下半部分与转鼓边缘贴合，在边壁摩擦力作用下受到牵引，呈现拉伸状态，从而导致其轴向二维切面形状变为椭圆形。根据可视化图像数据，皮革在周期性形变过程中，其质心会发生偏移，但该偏移对形变特征的影响很小，故在对皮革形变进行简化计算时不考虑该质心偏移的作用。

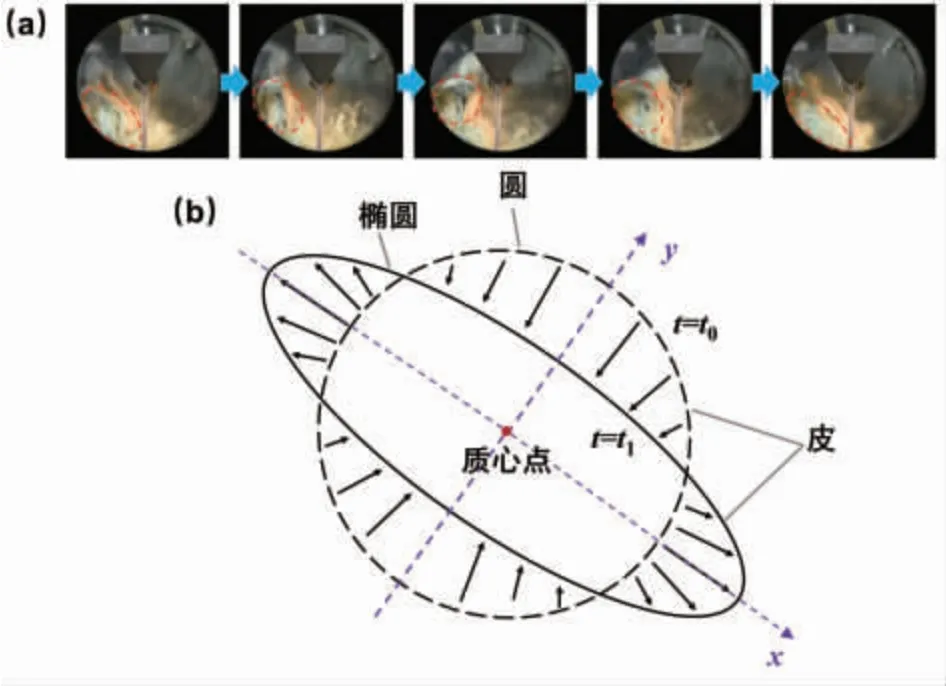
图1 皮革在鞣制过程中形变过程图像（a）及简化模型（b）Fig.1 Photos (a) and simplified model (b) of leather deformation process during tanning

1.1 形变计算模型

本文拟通过构建皮革在转鼓内的简化形变计算模型，研究皮革在转鼓内的运动与受力之间的关系。首先利用解析几何的方法，用数学表达式简化描述图1 中皮革的形变过程。此后，根据皮革在转鼓中的运动特征，构建皮革形变特性与运动特征、力学特征之间的关系。对计算模型进行如下简化：首先将三维柔性物体——皮革——简化为二维均质物体，周围流体为不可压缩牛顿流体，物理性质与水相同；其次将皮革在转鼓内复杂的形变过程简化为圆形变成椭圆形及椭圆形变成圆形的过程，局部的形变忽略不计。

以图1 的质心点为坐标原点，椭圆的长轴和短轴分别为x轴和y轴，建立坐标系。转鼓内皮革圆形态下轮廓线的方程见公式（1）：

其中，r 代表圆的半径。

皮革椭圆形态下轮廓线的方程见公式（2）：

其中，a表示椭圆的长轴，b表示椭圆的短轴，满足a＞b＞0。

在转鼓转动过程中，转鼓内皮革经历由圆形到椭圆形的变形，这个变形过程可以通过解析几何方程进行阐述，椭圆方程中的长轴a和短轴b与圆方程的半径r为周期函数的关系，且周期T=2（t0-t1），其中t0对应皮革处于圆形状态的时刻，t1对应皮革处于长轴最大值的椭圆状态的时刻。在皮革二维变形过程中，由于皮革的质量和密度均假设不变，因而其总面积S也保持不变，面积S的方程见公式（3）：

长轴a和半径r的关系可表示为公式（4）：

其中，m、n为常数，可根据椭圆方程求得；ω为角频率，等于2π/T；t为时间。

结合上述公式（3）和（4）可得到公式（5）：

皮革在转鼓内形变过程的动力学理论模型构建重点包括运动过程、形貌特征和受力分析。首先根据周期计算角速度ω，然后根据二值化处理后提取的皮革平面面积和周长构建皮革在转鼓内翻滚开始阶段的圆方程和结束阶段的椭圆方程。根据公式（6）计算翻滚开始阶段的圆方程中的半径r：

根据椭圆面积S公式（7）和周长L公式（8）计算翻滚结束阶段的椭圆方程中的长短轴。

此后，控制椭圆方程长轴a作为不变量，把短轴b作为校核量。将初始条件和过程条件代入公式（9）：

1.2 受力分析模型

对皮革在半径R转鼓内运动时的受力作具体分析，转鼓转动中心标记为O。因为转鼓内皮革的密度大于流体的密度，且自转速率n和皮革运动速率V较小，因此外力只需要考虑重力Fg、离心力Fe、支撑力FN、摩擦力Ff和推力F。转鼓在顺时针或逆时针旋转过程中，皮革沿着转动转鼓壁面相反的反向旋转，整体呈现一个变加速滑动特征。将皮革的质心C作为坐标原点，椭圆的长轴方向为x轴，短轴方向为y轴，对皮革在鞣制过程中的受力和质心位移状态进行计算，模型如图2 所示。需要说明的是，区别于形变特征计算，受力分析模型中需根据质心偏移量获取皮革在y方向的形变数据，以用于皮革的受力计算，该质心偏移数值由可视化图形数据处理得到。

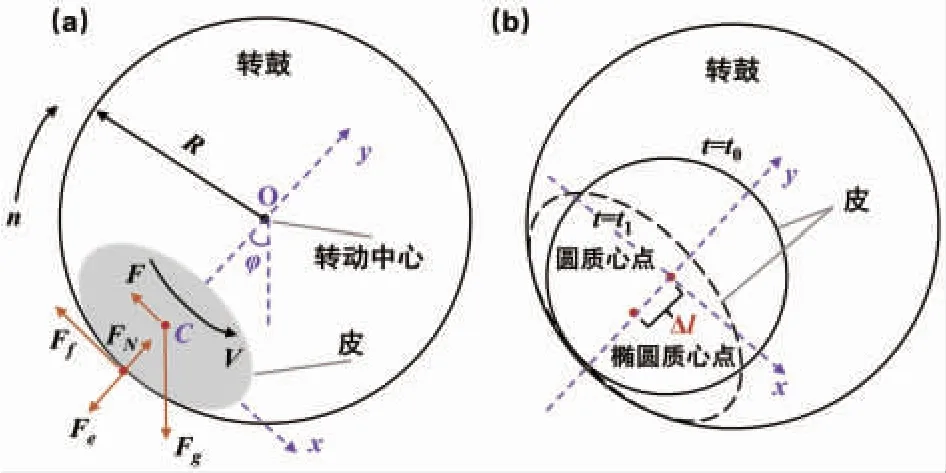
图2 受力分析（a）与质心位移（b）示意图Fig.2 Schematic diagram of force analysis (a) and displacement of the center of mass (b)

y方向上的外力包含离心力Fe、支撑力FN及压力（即重力沿鼓面法向的分力）Fg×cosφ，其关系见公式（10）：

其中，线段CO 为皮革质心与转动中心的连线，φ 是皮革质心偏角，即线段CO 与竖直方向的夹角。x方向上的外力包括推力F、有效重力的下滑分力Fg×sinφ 及摩擦力Ff，其关系见公式（11）：

其中，ax为皮革的切向加速度，mm/s2。

图2（a）显示，实际过程中引发皮革形变过程的力主要为转鼓提供的周期性推力F。皮革形状变为圆形时，推力的作用逐渐消失，在重力作用下沿x轴方向拉伸形变（即x轴方向半径r增大，逐渐形成椭圆形的长轴a），在挤压内力作用下沿y 轴方向挤压变形（即y轴方向半径r减小，逐渐形成的椭圆形的短轴b），最终变为一个椭圆。椭圆形的皮革在周期性推力的作用下长轴变短，在膨胀内力作用下短轴边长，逐渐又变为圆形。在由圆到椭圆，再由椭圆到圆的往复运动过程中，伴随着质心沿y轴方向的往复移动，皮革底部始终与转鼓壁面贴合。

图2（b）表示皮革处于形变过程中的质心偏移状态。假设任意时刻t时，皮革质心点沿着y 轴移动的位移值为x。与初始值t=t0时刻（皮革形状为圆形）的位移值相比，t=t1时（皮革形状为椭圆形）质心点沿着y轴移动的最大位移值为l，满足0≤Δl≤l。根据可视化图像数据处理结果，将质心位移简化为匀速过程，故Δl表示为公式（12）：

结合形变过程理论，可将形变过程曲线方程修正为公式（13）：

皮革发生形变的过程中，由于重力Fg大小和方向始终保持不变，沿x 轴方向的形变过程主要受到周期性推力F和摩擦力Ff的影响；沿y轴方向受到转鼓壁面的支撑力FN和皮革自身重力Fg的作用。期间，转鼓内皮革的面积始终保持不变。当周期性推力F减小时，皮革在摩擦力Ff的作用下沿x轴发生膨胀拉伸，又因为面积保持不变，所以在y轴方向必然存在挤压作用，该挤压作用促使皮革沿y轴方向产生挤压内力Finy，且该内力为弹性力，可由胡克定律求得。将皮革沿旋转方向的截面设定为内力作用面积S'。因此，该挤压内力Finy表示为公式（14）：

式中，S'为内力作用面积，m2；H为转鼓的深度，m；E0为皮革弹性模量，N/m2；b(t)为t时刻短轴的长度，m。

皮革沿x轴方向也存在膨胀内力Finx，可表示为公式（15）：

进一步推导出皮革形变过程中的受力平衡方程，其中沿y轴方向为公式（16）：

沿x 轴方向为公式（17）：

2 实验方法

2.1 实验试剂与仪器

浸酸牛皮（平均厚度h为1.5 mm），某制革厂提供；锆鞣剂，工业级，四川亭江新材料股份有限公司；GLS-D80 型泵热循环不锈钢控温试验转鼓（直径为0.8 m，深度0.4 m），无锡市荣浩皮革机械制造有限公司；D5600 型单反相机，广东尼康照相机有限公司。

2.2 实验流程

本实验参考前期工作[16-18]，采用典型锆鞣工艺对浸酸牛皮进行鞣制。取4 张浸酸牛皮分别标记为A、B、C、D，每一张酸皮分成4 块并进行标记（如A标记为A1、A2、A3、A4），然后再分成4 组（第1 组A1、B2、C3、D4；第2 组A2、B3、C4、D1；第3 组A3、B4、C1、D2；第4 组A4、B1、C2、D3），每组放进相同型号的4个转鼓内，将鞣制期间的转速分别设置为5、10、15和20 r/min。鞣制工艺条件简述如下：鞣制开始时，在转鼓中加入浸酸牛皮、锆鞣剂7%（以灰皮重计，下同）和浸酸液80%，转动4 h。用前期建立的转鼓中皮革运动的可视化方法[15]采集数据和视频，并进行可视化处理。

3 计算结果与分析

3.1 皮革形变特征

通过公式（9）计算求得m和n，将m和n代入公式（5），即可得到校核后的短轴b。然后利用皮革在转鼓内翻滚开始阶段和结束阶段的质心坐标，根据公式（12）求得Δl。将计算求得的m、n、r、Δl和ω等参数代入公式（13），可获得皮革在转鼓内翻滚运动状态的方程，至此皮革形变的解析方程计算完毕。

根据转鼓内皮革不同时间质心点的位移，绘制了长轴a和短轴b随时间变化的曲线，见图3。观察数据可以发现，不同转速下鞣制初期初始状态圆方程的半径r分别为112、121、110 和113 mm，而鞣制末期的半径r则分别为126、133、168 和132 mm。在鞣制初期，当转速为10 r/min 时，长轴a有最大的拉伸形变量，达到580 mm；转速为15 r/min 时，短轴b有最大的挤压形变量，为22 mm。在鞣制末期，当转速为5 r/min 时，长轴a仍有最大的拉伸形变量，达到805 mm，短轴b同样有最大的挤压形变量，为20 mm。

图3 鞣制初期和末期典型翻滚运动周期内长短轴a 和b 的变化（a）鞣制初期长轴a；（b）鞣制初期短轴b；（c）鞣制末期长轴a；（d）鞣制末期短轴bFig.3 Variation of long axis a and short axis b during the typical tumbling motion cycle at the beginning and the end of tanning(a)Long axis a at the beginning of tanning;(b)short axis b at the beginning of tanning;(c)long axis a at the end of tanning;(d)short axis b at the end of tanning

通过对比数据，可发现鞣制末期的皮革比鞣制初期的皮革更加舒展，因为在加工过程中皮革由于脱水变硬，质心沿y轴方向的位移量、初始状态圆方程的半径r、长轴a的最大拉伸形变量和短轴b的最大挤压形变量均比鞣制初期更大。此外，在鞣制初期，转速为15 r/min 时，长轴a和短轴b的变化速率均最大，平均变化速率分别为2 155 mm/s和438 mm/s。而在鞣制末期，转速为15 r/min 时，长轴a和短轴b的变化速率均最小，平均变化速率分别为955 mm/s 和242 mm/s；在5 r/min 时，长轴a和短轴b的变化速率均最大，平均变化速率分别为2 424 mm/s 和380 mm/s。

3.2 皮革受力分析

为了分析不同转速下皮革的翻滚运动状态，用简化的圆—椭圆模型进行受力分析。在y轴方向上，受力包含离心力Fe、支撑力FN、有效重力分解的压力Fg×cosφ 以及挤压内力Finy。在x轴方向上，受力包括摩擦力Ff、推力F、有效重力分解的下滑分力Fg×sinφ 以及膨胀内力Finx。在进行各个力的分析前，需要先明确不同作用力之间和作用力与转速内皮革形变之间的关系。随着转鼓转速的变化，各个作用力也会发生相应的变化。因此，需要研究各个作用力随转鼓转速的变化趋势，以便更好地理解不同转速下皮革的翻滚运动状态。

首先根据皮革质心坐标和转鼓中心坐标可求得皮革处于典型翻滚周期内的质心偏角φ，如图4 所示。根据测得的数据，在鞣制初期，5、10、15 和20 r/min 转速下皮革的平均质心偏角依次为55°、45°、61°和24°。这说明在鞣制初期，由于转鼓内皮革较软，在低转速下受到转鼓机械作用的持续时间长，但是相应的作用力更小，皮革发生形变导致的质心偏角是二者共同作用的结果，而15 r/min 的转速下可使皮革发生最大的形变。

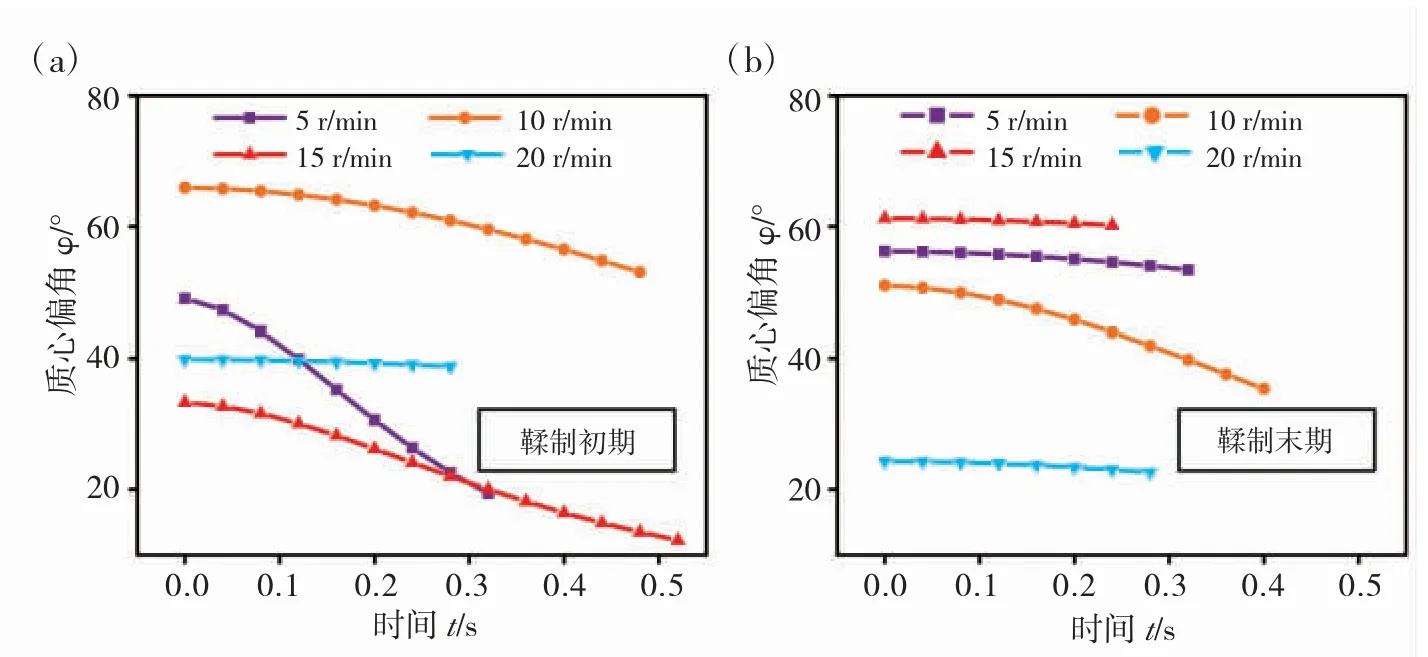
图4 鞣制初期和末期典型翻滚周期内皮革的质心偏角φ（a）鞣制初期；（b）鞣制末期Fig.4 Eccentricity φ of the center of mass of leather during the typical tumbling cycle at the beginning and the end of tanning(a)at the beginning of tanning;(b)at the end of tanning

在鞣制末期5、10、15 和20 r/min 转速下皮革的平均质心偏角依次为35°、61°、23°和39°。在皮革鞣制末期，皮革因鞣制效应不断增强的原因而变得较硬，因此转鼓对皮革的机械作用也发生了变化。数据显示，在此阶段中，皮革在5 r/min 的转速下具有最大的形变。这表明，随着鞣制过程的进行，其最佳转速会下降。因此，在皮革鞣制过程中，采用变速转动方案（即转速逐步降低）来改进生产过程，可能会实现最佳的鞣制效果。此外，由于翻滚运动期间皮革存在较大的质心偏角，会连续发生较大的形变，这有利于化学品的传质与吸收。因此，在制革过程中，通过控制转鼓的转速和翻滚运动的幅度，可望促进皮革化学品的传质，提升制革效率和效果。

依据理论计算模型并结合实验数据，可得到皮革各个受力的数值。结果表明，影响皮革加工的主要力包括膨胀内力Finx、挤压内力Finy和推力F，其余力的影响可忽略，上述3 个力的计算结果见图5（鞣制初期）和图6（鞣制末期）。在鞣制初期，Finx的最大值为1 054 N，对应转速为15 r/min；鞣制末期，Finx的最大值为1 549 N，对应转速为5 r/min。鞣制初期Finy的最大值为219 N，对应转速为10 r/min；鞣制末期，Finy的最大值为288 N，对应转速为15 r/min。从皮革进入翻滚状态开始，Finx和Finy的数值均先急剧增加然后趋于不变。该变化与圆-椭圆的形变过程直接相关，即随着挤压过程的持续，长轴a逐渐增大，且其变化速率逐渐变小。F的变化趋势同自身内力的变化趋势大体一致，在鞣制初期和末期，其最大值分别为980 N 和1 455 N，其对应的转速分别为15 r/min和5 r/min，与皮革出现最大形变的转速一致。

图5 鞣制初期不同转速下推力F、膨胀内力Finx 和挤压内力Finy（a）转速5 r/min；（b）转速10 r/min；（c）转速15 r/min；（d）转速20 r/minFig.5 Pushing force F, expanding force Finx and compressive force Finy at the beginning of tanning under different rotating speeds(a)5 r/min;(b)10 r/min;(c)15 r/min;(d)20 r/min

图6 鞣制末期不同转速下推力F、膨胀内力Finx 和挤压内力Finy（a）转速5 r/min；（b）转速10 r/min；（c）转速15 r/min；（d）转速20 r/minFig.6 Pushing force F, expanding force Finx and compressive force Finy at the end of tanning under different rotating speeds(a)5 r/min;(b)10 r/min;(c)15 r/min;(d)20 r/min

4 结论

本研究提出了一种用于转鼓内皮革的圆- 椭圆周期性形变理论计算模型，该模型可用于获取转鼓内皮革的形变和受力数据，并通过实验数据确定了该模型的特征参数，证明模型具有一定合理性。鞣制初期皮革较软，转速为15 r/min时，皮革具有最大的拉伸和挤压形变速率，分别为2 155 mm/s 和438 mm/s；鞣制末期皮革变硬，转速5 r/min 对应最大的拉伸和挤压形变速率，分别为2 424 mm/s 和380 mm/s。受力分析表明，影响皮革加工的主要力包括膨胀内力Finx、挤压内力Finy和推力F，其中推力F在鞣制初期和末期的最大值分别为980 N 和1 455 N，对应转速分别为15 r/min和5 r/min。因此，在初期使用高转速（如15 r/min），并在末期使用低转速（如5 r/min），可使皮革保持较大的形变和推力，从而获得更好的鞣制效果。

本研究通过分析鞣制过程不同转速和翻滚运动状态的皮革的形变和受力，并根据皮革形变程度越大越有利于化学品传质的原则，制定了皮革鞣制初期高转速、末期低转速的变转速加工方案。研究结果有望指导制革机械运行参数的科学合理配置，助力皮革行业的节能增效，并为皮革行业的数字化和智能化升级提供理论参考。