活用化曲为直法解带电粒子在电场中的运动问题
胡跃跃
(山东省滕州市第一中学)
带电粒子在电场中的运动问题是高考中的热点题型,年年必考,考查形式灵活多变,计算量较大,是很多学生比较头疼的题型之一.归纳发现,带电粒子在电场中的运动可以归为两大类型,即带电粒子在电场中加速或偏转运动和在涉及重力或磁场力作用的复合场中运动.学生之所以觉得题目难度大,是因为这类题目中带电粒子做的大多是曲线运动,而学生最擅长分析的往往是直线运动.既然如此,我们不妨使用“化曲为直法”来解题.
1 带电粒子在电场中加速或偏转运动
如果带电粒子是在匀强电场中做加速运动,我们可以用牛顿运动定律求解,也可以使用动能定理求解;而对于偏转问题,通常采用平抛运动的解题策略,该策略的核心就是“化曲为直”,相信大家都比较熟悉,当然,如果可以使用动能定理,那么解题会更加便捷.
例1如图1 所示,一个可以产生多种正离子(质子、氘核、氚核及氦核等)的粒子源被放置在加速电场的左侧,产生的正离子以极低速度进入加速电场,经过加速后的正离子从小孔S处沿偏转电场的极板A、B的中心线射入.已知加速电场的电压为U1,极板A、B的长度为L,极板A、B距离为d,偏转电场的电压为U2.若正离子能从极板A、B间射出(正离子的重力不计),则下列选项正确的是( ).
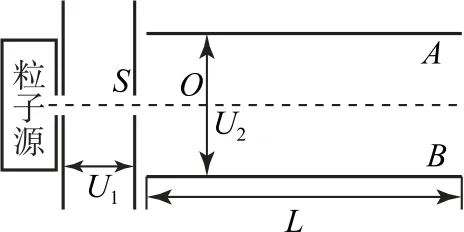
图1
B.不同粒子在满足题目条件的情况下,运动轨迹完全重合
C.不同粒子在满足题目条件的情况下,从偏转电场射出时的速度相同
D.不同粒子在满足题目条件的情况下,在两个电场中运动的时间相同在加速电场中可使用动能定理快速求出正离子的末速度,而在偏转电场中,需根据类平抛运动的规律逐项列式验证.
设正离子的电荷量为q,质量为m,从加速电场射出时的速度为v,根据动能定理得
将正离子在偏转电场中的运动分解为沿极板方向的匀速直线运动和沿垂直极板方向的匀加速直线运动,则沿极板方向有L=vt,沿垂直极板方向有y=,由牛顿第二定律得.因为正离子能从偏转电场射出,所以要满足:.
设正离子在偏转电场中沿极板方向运动距离x耗时t′,沿垂直极板方向的位移为y,有x=vt′,y=,结合上述结果,可得
由上式可知,正离子在偏转电场中运动的轨迹与离子的比荷无关,所以选项B正确.
由上面的分析可知,正离子垂直极板的分速度为
由速度的合成可得正离子射出偏转电场时的速度大小为
根据该式可知,正离子射出偏转磁场的速度与比荷有关,因此选项C错误.
设加速电场的宽度为s,则正离子在加速电场中运动的时间.正离子在偏转磁场中运动的时间,则正离子从进入加速电场到射出偏转电场所用时间为t3=t1+t2=.可见,不同正离子通过两个电场所用时间与比荷有关,所以选项D 错误.
小结虽然本题是一道选择题,但想要得到正确答案,计算量并不比一道计算题少.题目同时考查了带电粒子在电场中的加速和偏转问题,需要我们灵活运用牛顿运动定律、运动的合成与分解、动能定理等知识,且有较强的逻辑推理能力.
2 带电粒子在涉及重力或磁场力作用的复合场中运动
复合场是常见的题目情境.由于高中阶段研究的问题多为匀强电场、匀强磁场,复合场这类看似复杂的情境中却包含着最简单的本质,即带电粒子受到多个恒力作用,因此,我们可以运用熟悉的运动学知识加以分析,将曲线运动转化为熟悉的直线运动的合成,解题思路就变得清晰了.
例2如图2 所示,在方向水平向右、电场强度E=3×105N•C-1的匀强电场中,有一个倾斜角为53°的斜面底端与一个竖直放置的光滑绝缘的半圆轨道接触.图中O点为半圆轨道的圆心,A、B点分别是半圆轨道的上下端点.有一个质量m=0.4kg、电荷量q=+1.0×10-5C的小球(可视为质点)以初速度v0=10m•s-1从斜面上某点以垂直斜面的方向射出,小球恰好从A点进入半圆轨道.重力加速度g取10m•s-2,则( ).
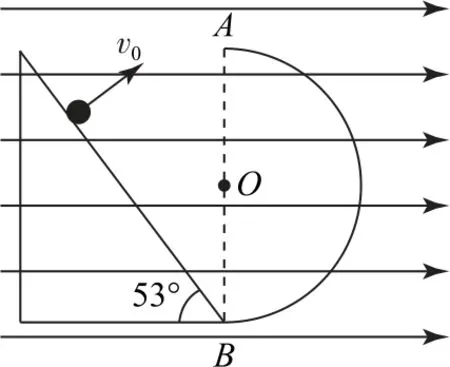
图2
A.小球从射出到运动到A点过程做类平抛运动
B.小球运动到A点时速度大小为12.5m•s-1
C.小球第一次在半圆轨道上运动过程中会在某处脱离轨道
D.小球第一次在半圆轨道上运动过程中对轨道的最大压力大小为33.5N
以小球为研究对象,其从起点运动到A点过程中对其受力分析如图3所示.小球受重力和水平向右的电场力作用,根据力的合成及几何知识可得F=5 N,方向沿斜面向下,所以小球从射出到运动到A点过程做类平抛运动,建立如图3所示的直角坐标系,在x轴方向小球做匀速直线运动,有vx=v0=10m•s-1.
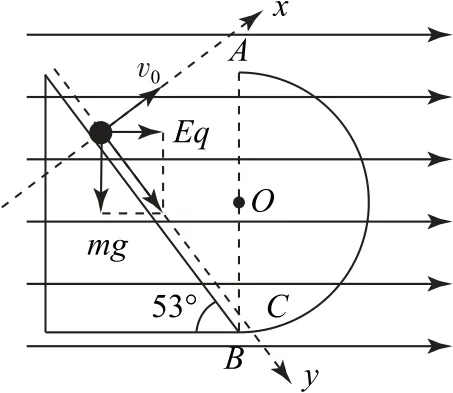
图3
小球从出发点到A点过程中偏转的角度为37°,根据几何知识可得在A点时小球的速度
如图4所示,图中C点代表小球运动过程中等效的最低点,即在C点处小球对轨道的压力最大,因为在A点时小球恰好进入轨道,即在A点未脱离轨道,则在其他位置也不会脱离半圆轨道.
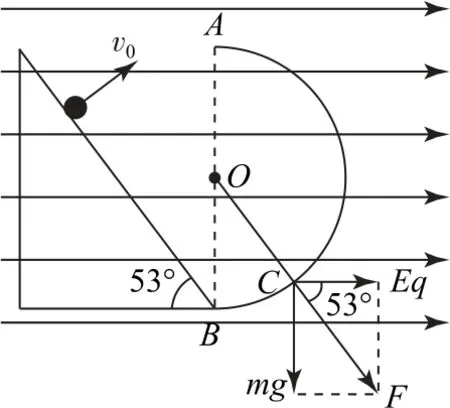
图4
在A点对小球应用牛顿第二定律得,从A点运动到C点过程中,根据动能定理可得
在C点有.联立各式解得FN=27N.
综上可知选项A、B正确.
小结本题是动能定理和圆周运动、平抛运动的综合,解题关键是找准各个过程遵循的物理规律.该题的化曲为直的方法主要体现在小球从出发点到A点的过程中类平抛运动的应用,尤其是对选项D 的分析,绕过了复杂的运动过程,直接应用动能定理使得问题变成从A点到C点的点对点过程,解题难点在于找到等效重力势能最低点.
化曲为直是一种化陌生为熟悉的常用解题思路和方法,我们要通过总结和迁移以做到灵活应用.
(完)
——碳正离子的产生及稳定性比较

