土壤表面与矩形截面柱宽带差值散射场研究

邓旭阳，任新成，朱小敏，杨鹏举，赵 晔

（延安大学 物理与电子信息学院，陕西 延安 716000）

粗糙地（海）面与目标的复合电磁散射特性在目标检测和精密制导武器等方面具有重要的应用价值，一直是众多学者研究的热点问题之一［1-3］。例如，在使用武器发射电磁波对低空飞行的目标进行检测的实际应用中，空中的不确定因素较多，这时的目标与背景环境之间存在着复杂的相互作用，从而导致实际应用出现困难，所以对于目标与粗糙地（海）面复合电磁散射特性的研究能够为这种类似情况提供理论依据。

近几十年来，国内外学者对于粗糙地（海）面与目标的复合电磁散射问题进行了大量的研究。O’NEILL等［4］研究了嵌入在随机各向同性有损电介质粗糙表面附近的良导体目标的电磁散射；MORGENTHALER等［5］利用半解析模式匹配算法，通过二维有限差分在频域对均匀平面波入射到包含掩埋电介质目标的随机粗糙电介质半空间上产生的散射进行了验证；EL-SHENAWEE［6］使用最陡下降快速多极方法，计算了埋藏在二维随机粗糙表面下的多个物体的散射；JAMIL 等［7］通过数值模型，研究了二维浮动目标的雷达散射截面的变化；赵勋旺等［8］利用多层快速多极子方法，计算地面上车辆目标的电磁散射特性；王蕊等［9］利用矩量法，研究了不同类型的土壤与埋藏目标的复合电磁散射问题；任新成等［10］运用矩量法，研究了带限分形大地土壤表面与部分埋藏目标的电磁散射；朱小敏等［11］运用时域有限差分方法，研究了一维有耗粗糙地面与上方多个目标的复合电磁散射问题；李科等［12］采用有限元-边界积分方法，研究了介质粗糙面上方涂覆目标的复合电磁散射特性。

综上所述，国内外学者对于目标与粗糙地（海）面的复合电磁散射问题研究得比较深入，但是对于目标与粗糙地（海）面的差值场散射问题的研究并不多见。

差值散射场这一理论由JOHNSON［13-14］提出，即计算粗糙面与其上方目标的空间散射场和粗糙面的空间散射场，并且求得两者差值，差值散射场既体现出了单独目标的体散射，也体现出了目标与粗糙面之间的相互作用。本文采用指数型分布的土壤表面，用蒙特卡罗方法进行模拟，土壤的介电特性利用四成分模型表示，并且将差值散射场理论加入到时域有限差分方法（FDTD）计算模型中，计算了粗糙土壤表面与其上方矩形截面柱的差值场散射特性，分析了入射角，矩形截面柱倾角、中心距土壤表面的高度、长和宽及尺寸对差值雷达散射系数的影响。

1 复合散射模型的建立

1.1 土壤表面轮廓建模

如图1 所示为复合散射模型的几何示意图，建立一平面直角坐标系，坐标原点为O，x轴正向水平向右，y轴正向竖直向上，x轴上方为自由空间，下方为各向同性均匀土壤，f(x)表示用蒙特卡罗方法［15］模拟生成的土壤表面，矩形截面柱ABCD位于土壤表面上方，ht为矩形截面中心距土壤表面的高度，矩形截面柱的AB边与x轴正向的夹角为φ。

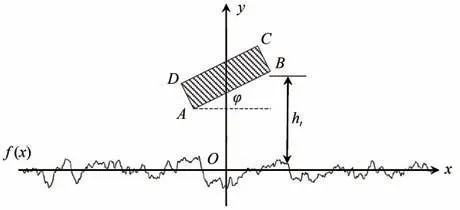
图1 土壤表面与矩形截面柱复合散射几何示意图

1.2 土壤介电常数模型

WANG 和SCHMUGGE 建立了四成分模型［16］，本文的土壤相对介电常数利用此模型来计算。下列两式为土壤的湿度压缩点Wp和临界体湿度mt的经验公式：

其中，S和C分别代表沙土和黏土含量，S+C≤100%。通常情况下土壤的岩石密度可取为ρs=2.65 g/cm3，ρb为干土壤密度，ρb由如下公式确定：

土壤的积孔率为

相对介电常数根据土壤湿度mv来计算，当mv≤mt时，

其中，εx=εi+(εw-εi)β，β=-0.57WP+0.481 为可调参数。εi、εr、εa=1.0 和εw分别为冰、岩石、空气和纯水的相对介电常数。εw由Debye公式计算：

其中，εω0为直流介电常数，τω为介质的弛豫时间。εω0和τω与温度的关系为

其中，T表示土壤温度。表1 列举了不同类型土壤的沙土和黏土含量［16］。

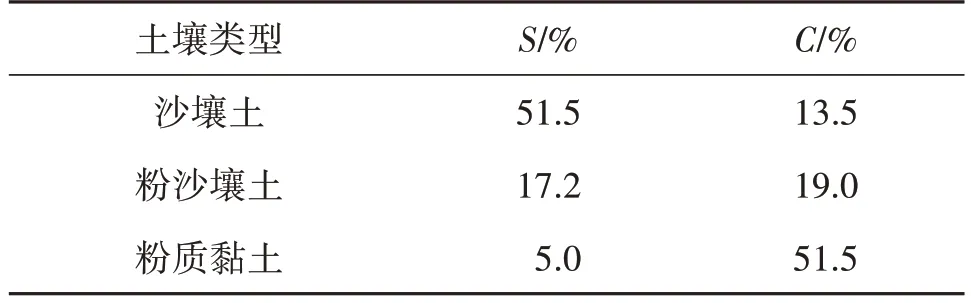
表1 不同类型土壤的沙土和黏土含量

本文中，土壤类型选择粉沙壤土，土壤介电常数取ε=10.291 3-i1.646 4，土壤湿度取mv=0.2 g/cm3。

1.3 目标建模

本文在计算时，目标建模为矩形截面柱，如图1所示。

2 FDTD方法

计算复合电磁散射的FDTD 模型如图2 所示，具体划分区域由参考文献［17］可见，本文不再赘述。

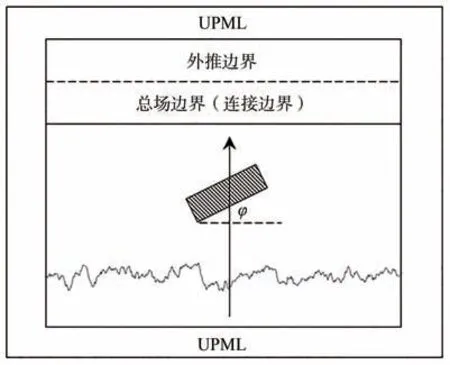
图2 土壤表面与矩形截面柱复合散射FDTD计算模型

本文以电磁波的TM波为例，FDTD差分公式为

式（11）～（13）中的详细取值见参考文献［17］。

本文选取高斯脉冲波为入射波，其表达式为

其中，τ为常数，决定高斯脉冲的宽度，通常选

对于差值散射场情况［18］，首先，由式（11）～（13）得出粗糙面的散射场Hx′、Hy′和Ez′，然后计算出土壤表面与矩形截面柱的散射场差值散射场可以由以下公式得出：

在式（15）～（17）中，差值雷达散射截面由Hx、Hy和Ez进行远近场变换得到。

归一化雷达散射截面的公式如下：

转化为散射系数：

即可得到差值雷达散射系数。

3 数值计算结果与讨论

在后面的计算中，选取50个粗糙面进行统计计算，粗糙面抽样长度L=160λ，网格宽度dx=0.05λ，入射角θi=30∘，矩形截面柱截面长AB=6λ，宽BC=2λ，倾角φ=0∘，目标中心距离土壤表面的高度ht=3λ，土壤介电常数利四成分模型进行计算，土壤类型选择粉沙壤土，取εr=10.291 3 -i1.646 4，土壤湿度取mv=0.2 g/cm3。土壤表面的高度起伏均方根δ=0.15λ，相关长度l=1.5λ，下面对各个情况进行讨论。

3.1 差值雷达散射系数随入射角的变化

图3为其他条件不变，入射角θi分别取0∘、30∘和60∘时目标在土壤表面上的差值雷达散射系数计算结果。由图3可知，差值雷达散射系数σ随频率f振荡地变化，在各个频点上θi=0o时的差值雷达散射系数σ最大，振荡的幅度最大，而θi=30o和θi=60o时的差值雷达散射系数σ均小于θi=0o时的σ，不仅如此，在有的频段θi=30o时σ大，而在另外一些频段，θi=30o时σ则小，而且，θi=30o和θi=60o时的σ的变化较小。

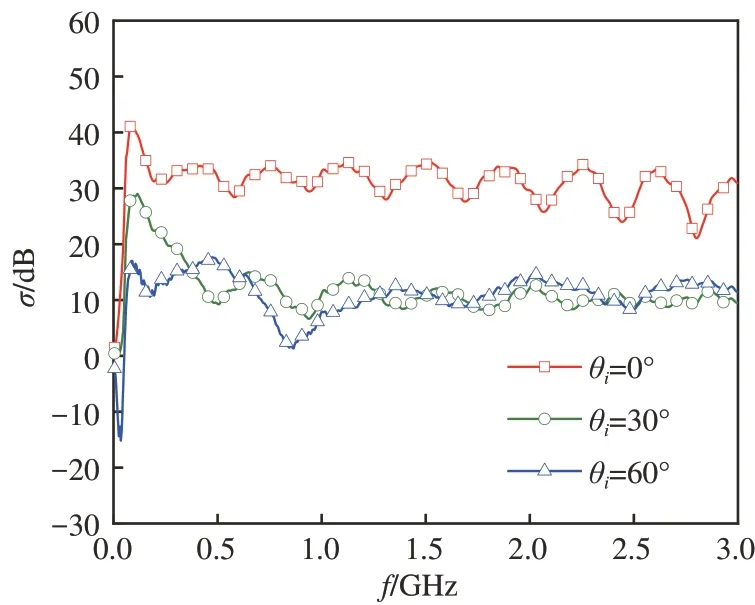
图3 差值雷达散射系数随入射角的变化

结合图1 可知，当θi取0∘时，入射波的方向垂直于矩形截面的CD边上，此时CD边的镜反射方向就是散射角为0∘的方向，因此出现了目标的前向散射增强效应，而当θi取30∘和60∘时，目标表面虽然均有镜面反射，但镜面反射的方向与前向散射的方向不一致，因此前向散射减弱。

3.2 差值雷达散射系数随矩形截面柱倾角的变化

图4 为其他条件不变，不同矩形截面柱倾角时目标在土壤表面上的差值雷达散射系数计算结果，倾角φ分别取10∘、30∘和50∘。从图4 可以看出，差值雷达散射系数σ随频率f振荡地变化，在各个频点上φ=30o时的差值雷达散射系数σ最大，振荡的幅度最小，而φ=10o和φ=50o时的σ均小于φ=30o时的σ，不仅如此，在有的频段φ=10o时σ大，而在另外一些频段，φ=10o时σ则小，而且，φ=10o和φ=50o时的σ变化较小。

图4 差值雷达散射系数随矩形截面柱倾角的变化

结合图1 可知，当φ=30o时，入射波的方向与矩形截面的CD垂直，此时散射角为30∘的方向恰好就是CD的镜反射方向，所以出现了目标的前向散射增强效应，而当φ=10o和φ=50o时，虽然也有镜面反射发生在矩形截面柱的表面，但是此时发生反射的方向与前向散射的方向不一致，因此前向散射减弱。

3.3 差值雷达散射系数随矩形截面柱高度的变化

图5为矩形截面柱中心距离土壤表面的高度对目标在土壤表面上的差值雷达散射系数影响的计算结果。其中高度ht分别取λ、3λ和5λ。由图5 可知，差值雷达散射系数σ具有一定的振荡幅度，并且随着f的增大而减小，当频率处于低频段时，ht对于σ随f振荡的幅度的影响相较而言比较大，当频率处于高频段时，ht对σ随f振荡的幅度的影响相较而言比较小。这是由于ht增大，矩形截面柱与土壤表面之间的相互作用增强。

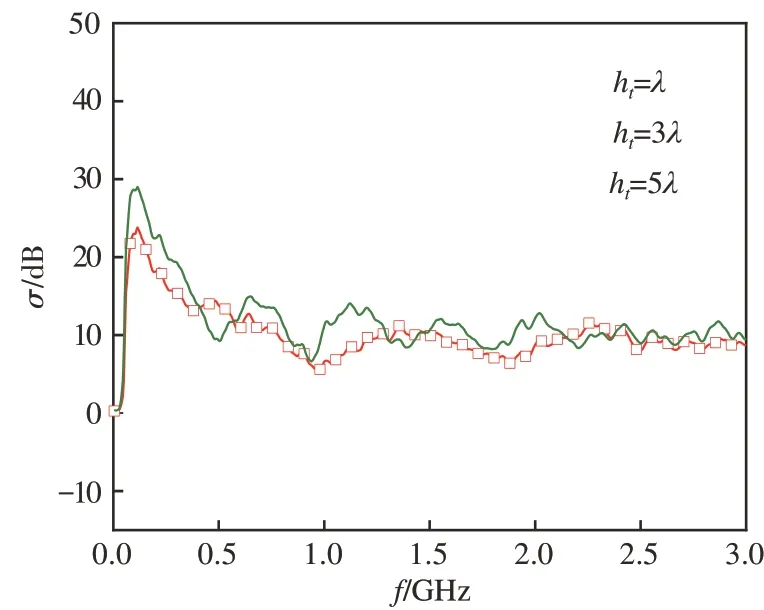
图5 差值雷达散射系数随矩形截面柱高度的变化

3.4 差值雷达散射系数随矩形截面柱尺寸的变化

图6为不同的矩形截面柱尺寸下目标在土壤表面上的差值雷达散射系数的计算结果。图6A中AB边长度分别取为4λ、6λ和8λ，图6B 中BC边长度分别取为2λ、4λ和6λ，图6C 中矩形截面柱等比例放大至原来（AB=6λ，BC=2λ）的2 倍、3 倍和4 倍。由图6A 可知，矩形截面柱AB边长度对于差值雷达散射系数σ的影响较小；由图6B 可知，矩形截面柱BC边长度对σ的影响较大，当f<1.3 GHz 时，σ随BC边长度变化的规律比较不明显，当f>1.3 GHz时，σ随BC边长度的增大而增大。这是由于目标的BC边长度增大时，目标BC面的镜面反射波增强，土壤表面与目标的相互作用增强，因此σ增大；由图6C可知，矩形截面柱等比例放大对于σ的影响较大，在低频区，σ随矩形截面柱等比例增大变化的规律较为复杂，而在高频区，σ随矩形截面柱等比例增大而增大，这种变化是由于目标的BC边长度增大时，目标BC面的镜面反射波增强，土壤表面与目标的相互作用增强，因此σ增大。

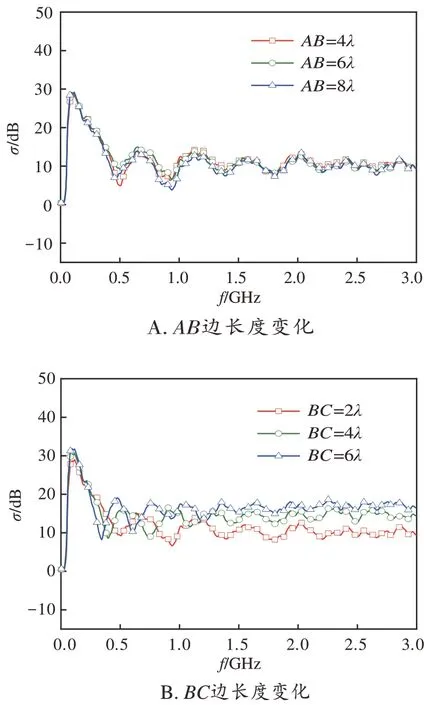
图6 差值雷达散射系数随矩形截面柱尺寸的变化

4 结论

本文基于FDTD 方法并且引入差值场散射理论，研究并分析了土壤表面与上方矩形截面柱复合模型的差值散射场特性，研究结果可用于求解目标与地（海）粗糙面的差值散射场问题，对地（海）表面的目标的识别、探测和监测均具有重要的应用价值。此外，使用FDTD 计算方法可以减少计算的时间和计算内存的占用量，相对而言FDTD 算法具有较高的准确性。因此，本文既可以解决一些实际的工程问题，又进一步推广了目标与地（海）粗糙面的复合电磁散射数值计算方法的理论，特别是目标置于土壤表面上的情况，与一些具体的实际工程问题比较贴合。本文目前研究的对象为一维土壤表面和二维目标，对于更复杂的目标与背景的复合电磁散射问题还需继续探索。