气液两相流过T型变径-直角弯头耦合管件压降特性的数值模拟研究

王艳芝，马文礼，王 帅

（延安大学 石油工程与环境工程学院；延安市油气高效管输与流动保障工程技术研究中心，陕西 延安 716000）

T 型、直角弯头作为常用的局部管件在油气管道输送领域发挥着十分重要的作用，而油、气、水等多相混合物在管道输送过程中流经此类局部管件时流动状态会发生急剧变化，进而可能会引起管道局部超压、流动掺混或分离加重、冲蚀腐蚀等影响管道安全输送的相关问题。由于多相流在经过该类管件时流动状态变化急剧，很难通过实验精确测量相关参数，因此以往大多数研究主要是数值模拟方面的研究，而且主要针对多相流动在T 型管件或直角弯头单独存在时的情况。其中，对于T 型管气固两相流，WILDE 等［1］在早期发现流化床提升管中的T 型管件会导致其出口产生回流，而且出口截面积越小，回流效应越强；包福兵等［2］则进一步指出T型管道直径越小，入口速度越大，整个流场压力损失就越大。对于油水两相流在T 型管内的流动特性，于爽等［3］发现在主管与垂直支管交汇处的局部阻力最大，而且其会随垂直支管管径的增大而增大。胡坤等［4］的研究表明在T 型管的主管和支管的连接处会同时发生油相聚集和油水分离现象。与油水两相流相比，气液两相流通过T 型管后会发生严重的相分离现象，该分离现象会增大侧支管的压力损耗［5］。SUN 等［6］的研究表明T 型管气液两相分布的均匀性随支管管径的减小而增加。FENG 等［7］则进一步指出作用在两相上的惯性力差的减小会促进垂直向上T形接头中气相分布的均匀性。对于直角弯管的气液两相流动，弯管中存在的独特的二次流现象对其流动特性及压降分布影响较大［8］。王志伟等［9］研究了90°弯管内气液两相流的流型演化规律，发现弯管二次流的分布与流型密切相关。陈浩宇［10］和王洪达等［11］研究发现弯管内的冲蚀现象也与二次流紧密相关，其会造成弯管外侧的冲蚀更加严重。MAZUMDER 等［12］讨论了气液两相在90°弯管中的压降特性，发现其与气相速度的相关性更大。汪冰等［13］进一步指出弯管压降损失最小的最佳弯径比会随雷诺数、含气率的变化有所不同。此外，ZAHEDI等［14］发现增加弯管的曲率半径可以使流动更加平缓，而减小弯管半径会使流动的旋转强度增加。关于弯管中的气液相分离特性，沈子木［15］发现液相的湍流强度会随含气量的增大而增强，同时气相的流通比也逐渐增大。同时，AUNG 等［16］的研究表明当液相速度较小时气液在弯管内的分离较快，且气相会迁移至弯管出口。综上所述，目前对于T型管或直角弯管气液两相流动特性的研究已经相对成熟，但关于气液两相流过T型-直角耦合管件流动特性的研究报道较少。因此，本研究基于FLUENT 软件，以西气东输二线某支线在试压排水过程中出现超压爆管现象所涉及的T 型变径-直角弯头耦合管件为例，分别开展不同入口压力、体积含气率及排水管径条件下，气液两相流过此类耦合管件的流动特性及压降规律研究，旨在为相关的油气储运工程问题提供理论依据。

1 数学模型及参数设置

1.1 数学模型

本研究所涉及的流动介质为空气-水两相流，可能存在的主要流态是气泡流。因此，采用FLUENT软件中的多相流Mixture混合模型，不考虑相间滑移速度，忽略重力的影响，简化为均相流模型来处理。那么用于求解两相流动的连续性方程和动量方程分别为

其中，ρm和ρk分别为混合密度和第k相的密度，分别为质量平均速度、第k相的速度和飘移速度，m/s；n为相数；αk为第k相的体积分数；μm为混合黏性系数，Pa·s；F→为体积力，N。

1.2 几何参数

图1 为T 型变径-直角弯头耦合管件的几何结构示意图，其中水平部分的粗管路为天然气管道末端部分，直角弯头部分为排水管路。相关尺寸为：T型管部分的入口管径D1=1.18 m，直角弯管的出口管径D2采用3 种系列，外径分别为159、273 和355 mm。其他尺寸为L1=15 m，L2=1 m，L3=1.66 m，L4=2.07 m。气液两相流从T 型结构部分的水平管路入口进入，从直角弯头管路的出口流出。

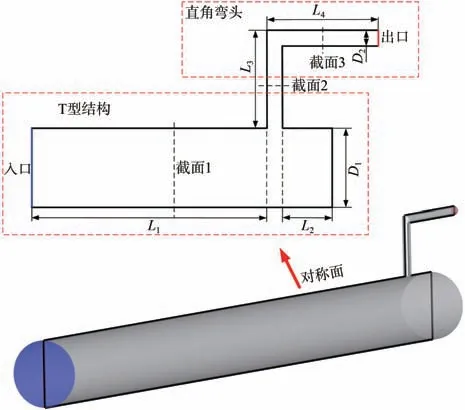
图1 T型变径-直角弯头耦合管件的几何结构示意图

在对最终的计算结果进行后处理时，选取了3 个参考位置来计算气液两相流经过该耦合管件的局部压降，分别为T 型结构上游距直角弯头垂直段0.5 m 的位置（截面1）、直角弯头竖直管部分中间点位置（截面2）、直角弯头排出管路下游0.5 m 的位置（截面3）。将截面1和截面2之间的压力差值作为T型结构的压降，将截面2 和截面3 之间的压差作为直角弯头结构的压降，将截面1 和截面3 之间的压差作为整个耦合结构的压降，截面的位置分布如图1所示。

1.3 网格参数

由图1 参数可知，本研究的几何模型为管径比较大的T 型变径管和管径比较小的90°弯头的耦合结构，模型相对复杂，故采用非结构化对其进行网格划分，并在T 型结构变径处及直角弯头位置进行网格加密处理。整个几何模型划分的网格数量为200 万左右，80%以上的网格质量都在0.7 以上，基本符合工程计算要求。

1.4 求解参数

对于空气和水组成的气液混合物，相关参数均按常压条件设置。其中，空气密度为1.225 kg/m3，黏度为1.789×10-5Pa·s；水的密度为998.2 kg/m3，黏度为0.001 003 Pa·s。由于管路大部分水平放置，而且直角弯头的竖直管路部分相对较短，管径也很小，因此这里忽略两相流重力的影响。湍流模型采用Realizablek-ε模型，壁面函数采用标准壁面函数法，方程离散采用一阶迎风格式。选择FLUENT软件中分离式的求解器，采用隐式SIMPLE 压力耦合算法。对于亚松弛迭代因子，压力修正项初始设置为0.3，动量修正项设置为0.7，含气率设置为0.5。在计算的过程中，根据收敛情况，确定是否对松弛因子进行调整，收敛残差标准均设为10-6，但在计算过程中往往未达到这个收敛标准时残差曲线就趋于水平了，这时根据进出口流量差来确定是否收敛，当进出口流量差小于进口流量的1%时即可认为收敛。对于边界条件，进出口均采用压力边界，其中出口压力设置为常压，壁面边界采用无滑移边界条件。

2 结果与分析

本研究主要考虑入口压力（0.3、0.5、0.7和0.9 MPa）、体积含气率（0.1、0.2、0.3和0.4）以及直角弯头管径（排水管径）（159、273和355 mm）等3个影响因素，基于正交实验设计了48 种模拟工况。并依据不同工况的模拟结果来探讨不同影响因素对气液两相流过T型变径-直角弯头耦合管件压降特性的影响规律。

2.1 流场分析

为理解气液两相流在T 型变径-直角弯头耦合结构中的流动特性，以排水管径为273 mm，入口压力为0.7 MPa，含气率为0.1 的工况为例对整个耦合结构内的流场分布进行分析。图2 为T 型变径-直角弯头耦合结构对称面（末端部分）上的绝对压力和速度分布云图。由图2A 可知，T 型结构水平管路部分整体压力分布比较均匀，而在其垂直管路部分压力存在局部集中的现象，但其整体压力要大于直角弯头水平出口管路部分。直角弯头部分由于直径相对较小，对应的承压能力整体也较低，因此局部超压现象最可能出现在垂直管路部分。结合图2B 可以发现，在T型结构垂直管路部分的左侧区域两相速度较低，而该区域内的压力相对较高。相反，T型结构垂直管路部分的右侧区域速度较大，但压力较低，这表明T 型变径结构部分的压降损失主要发生在其垂直管路部分的右侧区域。直角弯头水平管路部分的下部区域两相速度较小，压力也较低甚至出现负压，说明该区域内能量损失严重，是直角弯头管路压力损失的主要部位。

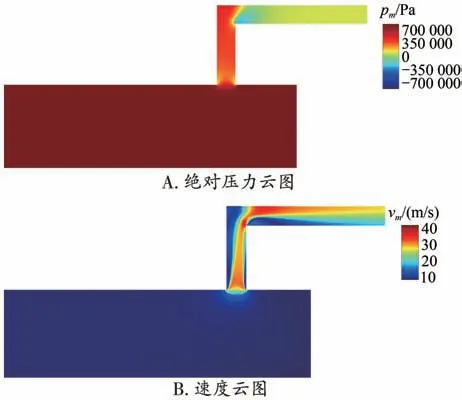
图2 T型变径-直角弯头耦合结构对称面（末端部分）上的压力和速度分布云图

图3 为T 型变径-直角弯头相连接的垂直管路中间截面2上的压力和速度分布。由图3A 可知，截面左半部分压力较高，右半部分压力较低，但数值相差不大。由图3B可知，压力较高的区域对应的流体速度较小，而压力较低的区域对应流体速度较大。同时，在该截面上观察到了明显的二次流现象，可以携带低动量的流体从高压区流向低压区。此外，该二次流有两个涡心并关于水平对称轴上下对称，在低压力的区域二次流速度较大，其也是造成压力损失的主要因素之一。

图3 T型变径-直角弯头耦合结构中间截面2上的压力和速度分布云图

同理，图4 为T 型变径-直角弯头耦合结构出口截面3 上的绝对压力和速度分布云图。由图4A 可知，耦合结构出口截面3上的压力分布不均匀，且整体数值较小，大部分区域处于负压区。结合图4B可以发现，在压力为负的区域相应的速度值较大，同时该区域内的二次流速度也较大。由此可知，较大的流向速度以及较强的二次流涡是造成压力损失的主要原因之一。

图4 T型变径-直角弯头耦合结构出口截面3上的压力和速度分布云图

2.2 入口压力的影响

图5以排水管径为159 mm 的情况为例，给出了T型结构、直角弯头及整个耦合结构的压降损失随入口压力的变化规律。由图可知，气液两相流经过T型结构、直角弯头及整体耦合结构的压降损失均随着入口压力的增加基本呈线性增加的趋势。含气率的变化对整体的压降损失影响较小，但当含气率为0.2时，T型结构和直角弯头的压降损失随入口压力的增加偏离了线性变化，这说明含气率的影响仅在一定压力范围内才能体现出来。另外，对比不同结构压降损失的具体数据可以发现，在耦合结构的压降损失中，直角弯头部分的压降损失占整个耦合结构压降损失的2/3左右，而T型结构的压降损失仅占1/3，这与前面流场分析得到的结果保持一致，主要是由于直角弯头区域的二次流涡效应更强，进而造成的压降损失更大。因此，在实际的相关油气储运过程中，可以通过降低入口压力来降低耦合管件的压降损失，从而降低储运风险。

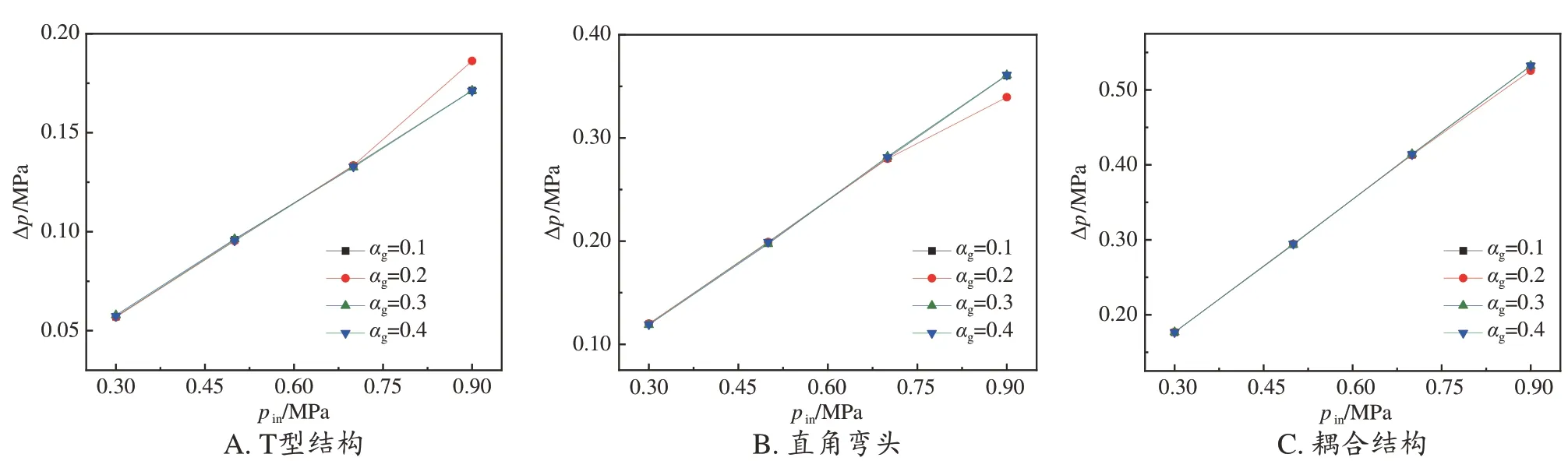
图5 排水管径为159 mm时局部压降随入口压力的变化情况

当排水管径为273和355 mm 时，所得到的流体经过T 型结构、直角弯头及整个耦合结构的压降损失随着入口压力的变化趋势均与排水管径为159 mm的情况基本类似，这里不再赘述。通过对比3 种不同排水管径耦合结构的压降损失数值发现，随着排水管径的增大，直角弯头部分的压降损失几乎没有发生改变，而T型结构部分的压降损失逐渐减小，这说明排水管径的变化对T型结构的影响较大。

2.3 体积含气率的影响

图6以排水管径为273 mm 的工况为例，给出了不同构件区域的局部压降随含气率的变化情况。由图可知，T型结构、直角弯头及整个耦合结构的局部压降损失均随着含气率的增加而在小幅度范围内上下浮动，影响很小，这主要是由于含气率对气液两相混合物流场的影响受多方面因素的影响，对压降的影响并不呈线性变化。

图6 排水管径为273 mm时局部压降随含气率的变化情况

可通过各部分构件的局部压降随含气率的最大变化值占局部压降均值的百分比（σ）进一步说明不同含气率对压降损失的影响。最大百分比σ计算公式如下：

其中，δ为局部压降随含气率的最大变化值，Pa；Δp为各局部构件随含气率变化的压降均值，Pa；

表1为各部分构件局部压降随含气率最大变化值占局部压降值的百分比情况。由表1 可知，各部件局部压降随含气率变化的最大百分比为1.778%，因此在同一入口压力下含气率对局部压降的影响非常小。另外，随着入口压力的增大，T 型结构和直角弯头的最大压降百分比均逐渐下降，这说明管内压力较大时，含气率对局部压降的影响较小。与T 型结构或直角弯头相比，整个耦合结构由于含气率变化引起的最大压降百分比值最小，这表明含气率变化对整个耦合结构的压降损失影响较小。

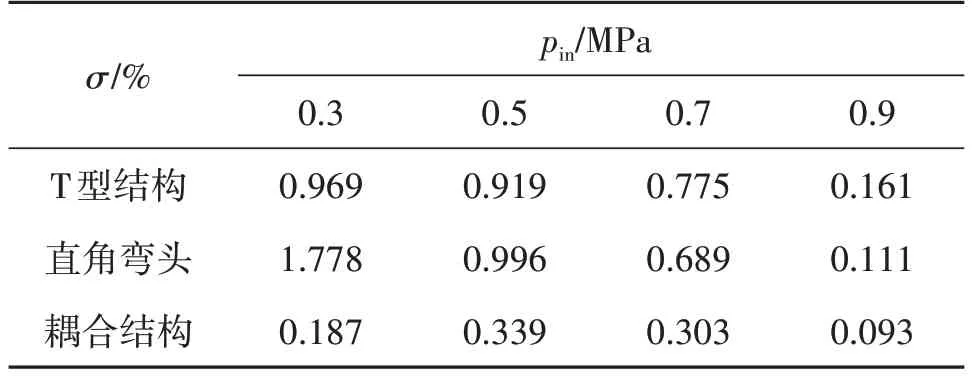
表1 耦合构件各部分局部压降随含气率的最大变化值占局部压降值的百分比

2.4 排水管径的影响

图7 为不同入口压力下耦合结构局部压降随排水管径的变化情况。由图可知，气液两相流经过T 型变径-直角弯头耦合构件的局部压降损失随直角弯头管路直径的增大而减小，但减小的幅度越来越小。这是由于随着排水管径的增大，T 型弯头的变径截面处及直角弯头流体变向处的二次流强度减弱，从而使局部压降减小。结合前面的分析可知，耦合结构整体压降的减小，主要是由于T 型弯头部分的压降减小造成的。另外，从图7 可知，当排水管路直径从159 mm 变为273 mm 时，含气率几乎对局部压降没有影响，但在管径从273 mm 变为355 mm 时含气率对局部压降的影响逐渐显现出来，而且含气率越大，局部压降越小。这主要是由于随着含气率的增大，混合相的黏度越来越小，因而局部摩阻减小，压降损失也就减小。总之，在实际油气储运中，直角弯头管径是影响压降损失的一个重要因素，可通过增加直角弯头管径达到降低压降损失的目的。

图7 不同入口压力下耦合结构局部压降随排水管径的变化情况

3 结论

1）对于T 型结构部分，在其垂直管路左侧区域两相流的压力较高，速度较小，而在其右侧区域速度较大，压力较低，两相流在该结构内的压降损失也主要发生在该区域。对于直角弯头部分，其弯头下部区域两相流速度较小，压力值为负，是压力损失的主要部位。T型结构垂直管路及直角弯头水平管路中的二次流涡是造成气液两相流过T 型变径-直角弯头耦合管件能量损失的主要来源。

2）随着入口压力的增大，气液两相流过T 型结构、直角弯头及耦合结构的局部压降逐渐增大，其中直角弯头部分的压降损失占整个耦合结构压降损失的2/3，而T 型结构的压降损失占1/3。在实际油气储运过程中，可通过降低入口压力来达到降低压降损失的目的。

3）随着含气率的增加，气液两相流过T型结构、直角弯头及整个耦合结构的局部压降损失均在小幅度范围内上下浮动。随着压力的增大，含气率对局部压降损失的影响变小，而随着排水管径的增大，含气率对局部压降的影响逐渐变大，而且含气率越大，局部压降越小。

4）随着排水管径的增大，气液两相流过T 型变径-直角弯头耦合结构的局部压降逐渐减小，但减小的幅度变小。在实际油气储运过程中，可通过增加直角弯头管径达到降低压降损失的目的。