垂直上升管内气水两相流动截面含气率试验

张 理，随志强，周 翔，黄世苗

（1. 南方海洋科学与工程广东省实验室（湛江），广东湛江 524000；2. 上海船舶设备研究所，上海 200031）

0 引言

在动力、石油、化工和制冷等工业设备中经常遇到气液两相流体的流动工况，而截面含气率是气液两相流中最重要的特性参数之一，在流动压降计算和传热特性计算中占据十分重要的地位。比如在泡状流和段塞流中，垂直上升管中的重位压降可占总压降的90%以上[1-2]，而要准确计算重位压降，则必须建立截面含气率的高精度计算式。目前，测量气液两相流截面含气率的方法主要有快关阀门法、射线法、电学法、光导探针法、压差法和层析成像法[3-4]。快关阀门法对阀门的性能和同步性要求较高，需要同时关闭2个阀门[5]，无法实现自动测量。对于压差法，考虑流型的影响，建立水平段摩擦压力降替代垂直上升段摩擦压降间的修正关系式，以减小直接替代引入的误差，是差压法测量截面含气率的关键[6]。电学法和光学法干扰流场，高温下探测元件精度低[7]。层析成像法测量出的截面含气率值精度高，但操作较复杂，气液两相接触界面的信号处理存在难点[8]。射线测量法是利用射线在穿过不同密度介质时衰减程度不同来测量，不会破坏管道中的流场和温度场的自然分布[9]，是一种非接触式测量方法，使用简单，精度相对较高。

气液两相流截面含气率的计算方法主要分为均相模型法和分相模型法。均相模型法假设气液两相流速相等，截面含气率与体积含气率相等。分相模型法主要分为：1）基于均相模型的修正，如阿尔曼特方法；2）使用滑移比S计算截面含气率α，如奥斯马奇金公式、米洛波尔基公式和汤姆计算法；3）使用截面含气率模型计算α的方法，如Smith的均相-单相并流模型、Wallis漂移模型、Bankoff变密度模型和Zuber-Findlay漂移模型。

笔者采用伽马射线法对常温常压垂直上升管两相流截面含气率进行研究，分析了截面含气率随折算气速、体积含气率的变化。通过伽马射线法测量值与文献中常用的一些经验公式和理论模型进行对比分析，对常温常压下气水两相流截面含气率的进一步研究和含气率的计算提供一定的参考价值。

1 试验系统

试验系统如图1所示，试验工质选用空气和去离子水，试验中去离子水从水箱经过滤器和循环水泵，一部分从主路流经电磁流量计进入试验段，一部分经旁路流回水箱。空气由压缩机压出后，经稳压罐和过滤器流经质量流量计，气液两相在试验段前端的混合器混合均匀后经稳定段进入试验段。从试验段流出的两相流体经过换热器后进入水箱，空气由于浮升力作用而排出，水进入水箱后进行循环流动。

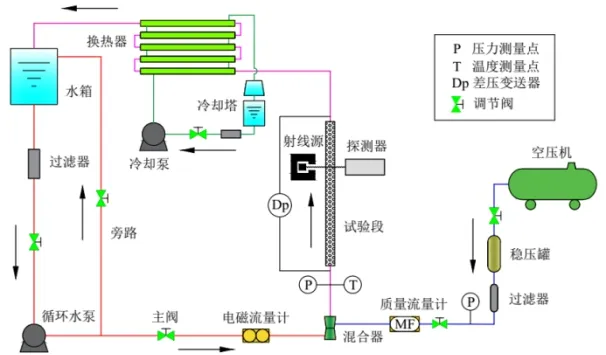
图1 常温常压空气-水两相流试验系统

试验气流量采用的质量流量计量程为0～100 L/min，试验前用玻璃转子流量计进行标定。水流量是采用电磁流量计测量，试验段压力、温度和压差分别采用压力变送器、T型热电偶和差压变送器测量，输出的所有信号由IMP数据采集系统采集，并联接计算机进行记录。

试验时，先固定水流量，气流量从小到大调节并进行测量，每调节一次，待工况稳定后，在电脑上采集探测器接收到的伽马射线计数率以及IMP数据采集系统的信号。采集完成后，调节水流量，并从小到大调节气流量进行下一个工况的测量，直至完成所有工况的测量。

2 试验原理与测量方法

2.1 试验原理

伽马射线在传播过程中强度逐渐减弱，在穿透介质时与介质相互作用会使强度有所衰减，衰减值与被测介质分布有关。射线法测量两相流截面含气率的基本原理是：依据射线在物质中衰减的Beer-Lambert定律。

式中：I0为被测介质吸收前的射线强度；I为被测介质吸收后的射线强度；μ介质对射线的线性吸收系数；x为介质的厚度。

设伽马射线透过气液两相流管道（见图2），射线在未进入管道时的射线强度为I0, 透过两相流管道后的射线强度为I，根据Beer-Lambert定律，有

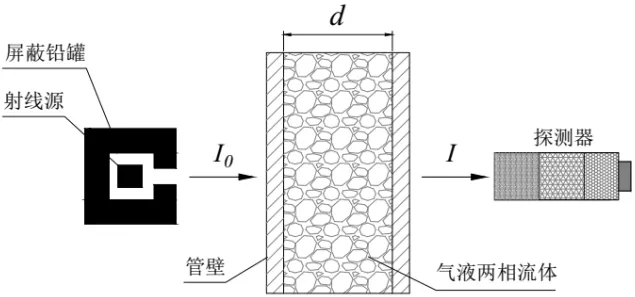
图2 伽马射线法测量截面含气率的原理图

式中：μ1、μ2和μ3分别为管壁、液体和气体的线性吸收系数；d为两相流管内径；x为管内气体占有的截面长度；δ为两相流管壁厚度。

而后分别测量管道内充满液相和气相时同样强度的射线I0，透过管道后强度I1和I2，根据式（1）可得

联立式（2）、式（3）和式（4），并由截面含气率的定义，可得

在伽马射线测量系统中，射线在不同情况下的强度一般是用相应的计数率代替，即可用Nm、Nl和Ng代替I、I1和I2，则利用伽马射线衰减技术测量两相流空泡份额的公式为[10]

式中：Nm为伽马射线穿过试验段中空气-水两相混合物后的计数率，s−1；Nl和Ng分别为伽马射线穿过试验段中全部为水时和全部为空气时的计数率，s−1。

通过测量伽马射线穿过试验段3种工况的计数率，由式（6）可求得相应工况下的α值。

2.2 测量方法

试验段圆管材料为有机玻璃，内径为15 mm，伽马射线的测量系统如图3所示，放射源采用CS-137，活度为1.63×108Bq，闪烁晶体采用碘化钠（NaI），具有很高的探测效率。计数器每秒采集10次，每个工况采集3组，每组采集20 s。环境温度对闪烁体有影响[11]，在试验过程中需要保持恒定温度。整个试验系统处于室温环境下，温度变化不大，可以满足闪烁晶体的测量要求。闪烁晶体、光电倍增管和放大器嵌入到钢管中就组成了探测器的主体部分。在试验开始前，需要采集试验段全液相和全气相的本底计数率，多次测量求取平均值。

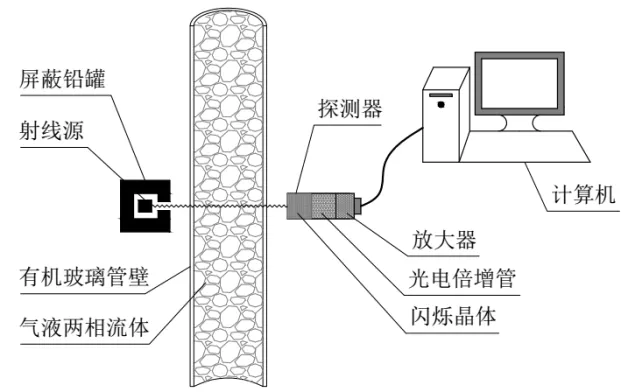
图3 伽马射线测量系统图

3 试验结果与分析

3.1 本底计数率基准的确定

为了提高伽马射线测量的精度和求取截面含气率，需要采集伽马射线测量系统在试验段工质为全液相和全气相时的计数率，采集时间分别为120 s。经统计分析，当试验段全部充满水时，液相本底为17 807；当试验段全部充满气时，气相本底为18 602。当试验段为单相流体时，计数率波动不大，相对偏差小，以此可作为液相本底和气相本底的基准。

3.2 截面含气率随折算气速和体积含气率变化

通过式（6）计算获得了伽马射线法的截面含气率值，试验中不同折算水速下截面含气率随折算气速的变化情况如图4(a)所示。从图4(a)中可以看出，在同一折算水速下，在低折算气速usg＜0.8 m/s的小范围内，折算水速较小的增加会造成截面含气率较快的增大，变化较明显；在折算气速usg＞0.8 m/s后，截面含气率随着折算气速的增大而缓慢增大。其他研究者对于截面含气率随着折算气速的变化也发现有相似的趋势[12-14]。同一折算气速时，截面含气率随着折算水速的增大而减小，且折算水速之间相差越大，这种变化越明显。

分析曲线的变化，截面含气率受折算气速和折算液速影响比较大。在水速一定，低气速下，空气与水相互作用强烈，气速是影响截面含气率的主要因素，气速的较小增加都会造成截面含气率的较快增加。此时，管内流型主要为泡状流和弹状流，当流型为弹状流时，管内多为连续的气弹和尾流，会造成截面含气率的较大波动。在气速一定时，随着水速的增大，气泡被冲散在水中，水的份额占比逐渐增大，水速是影响截面含气率的主要因素。所以在低液速时，水速对截面含气率的影响作用不是很大，而液速变大时，这种影响效果变得很明显。

试验在不同折算水速下所得的截面含气率与体积含气率的关系如图4(b)所示，图4(b)显示了在不同的折算水速下伽马射线法所测得的截面含气率比体积含气率小。同一折算水速下，在β＜0.9时，截面含气率随着体积含气率近似呈线性增长；在β＞0.9时，截面含气率随着体积含气率的增大而显著增大。

图4 截面含气率随折算气速和体积含气率的变化

3.3 试验结果与经验公式对比

将通过（6）式计算所得的伽马射线法截面含气率值与文献中一些经验公式和理论模型所预测的截面含气值对比，结果如图5所示。从图5中可以看出，多数关联式所预测的截面含气率值与试验测量值的偏差在−30%～30%，均相模型法预测值都偏高，部分预测值与测量值偏差大于30%。奥斯马奇金计算法多数预测值都偏低，部分预测值与测量值偏差低于−30%。

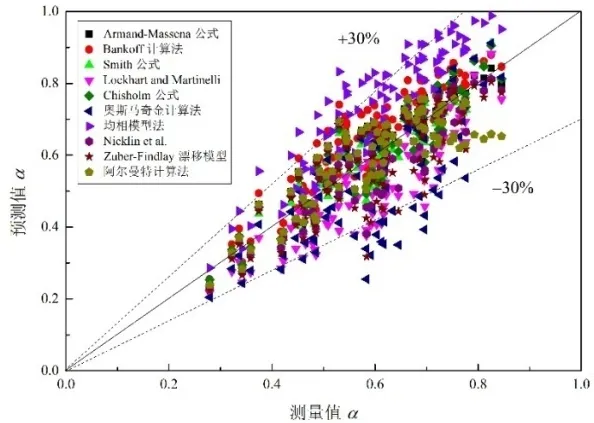
图5 经验公式预测的截面含气率与伽马射线法截面含气率对比

本文从10个预测关联式中选择了4个典型的理论公式进行截面含气率的预测，并与伽马射线法所获得的截面含气率值进行对比分析。

均相模型是将气液两相流体看成具有相同流速的均匀混合物，适用于气液两相在管道截面分布较为均匀的泡状流和雾状流。通常采用均相模型计算截面含气率的结果的可信度不高[15]。均相流修正系数模型主要是指在均相模型的基础上乘以一个常数或修正关系式得到的截面含气率预测模型[16]。目前比较常用的是Armand-Massena关联式：

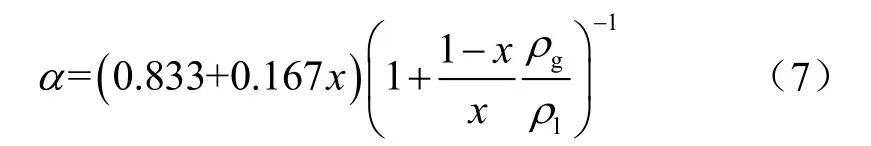
式中：α为截面含气率；x为质量含气率；ρg和ρl分别为气相和液相的密度，kg/m³。

Smith提出了一种均相单相并流的流动模型，模型假设管壁上流动的为单相水膜，管子中间流动的为均相汽-水混合物。在压力P＝0.1 ～14.8 MPa，质量流速ρu＝650～2 500 kg/(m²·s)，管子内径为6～38 mm情况下，误差为±10%[17-18]。Smith法截面含气率计算式为式（8）中：e为均相混合物中水的质量和水流质量之比，Smith求得当e＝0.4时，α值与大多数试验值比较符合。

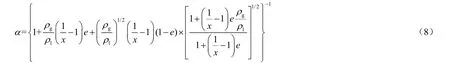
BANKOFF[9]提出了一种变密度模型，模型假设气泡悬浮于液体中，并假定气相浓度和混合物流速均沿管道截面按指数曲线分布，壁面处为零，管子中心处最大，气液之间无相对运动。Bankoff基于变密度模型，推导了管子截面上的平均截面含气率[19]，计算为

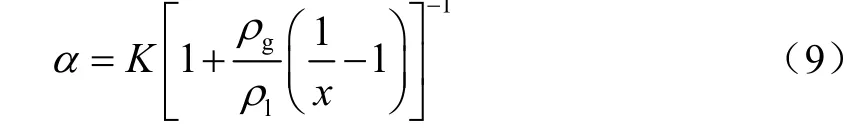
WALLIS[20]根据漂移速度的定义，建立了Wallis漂移模型。但Wallis模型是一维的，没有考虑流速和截面含气率在流道截面上的变化，只考虑了两相之间的滑移，应用上具有一定的局限性。Zuber-Findlay漂移模型也以漂移速度为基础，但既考虑两相流速不等，又考虑沿流道截面每一相的流速与截面含气率也有一定的分布[21-22]，考虑了气液两相不同速度分布以及α沿管子截面分布不均匀性对计算整个截面平均含气率的影响。Zuber-Findlay漂移模型的截面含气率计算为

图6比较了Armand-Massena法计算值、Smith法计算值、Bankoff公式计算值和Zuber-Findlay漂移模型计算值与伽马射线法截面含气率测量值。从图6(a)可以看出：Armand-Massena法计算值与伽马射线法测量值吻合性最好，相对误差范围为−15～20%，预测值与测量值比较接近。从图6(b)可以看出：Smith法计算值与伽马射线法测量值吻合性好，相对误差范围是−20～20%。比较图6(a)和图6(b)，在0.25＜α＜0.75时，Armand-Massena法与Smith法的预测值与测量值基本一致；在α＞0.75时，Armand-Massena法计算值比Smith法计算值更接近测量值。图6(c)显示：Bankoff公式法的大部分计算值都比测量值要大，最大相对偏差为30%，对于0.25＜α＜0.85的绝大部分，偏差较大。图6(d)显示Zuber-Findlay漂移模型的大部分计算值都小于测量值，而且较为分散，最大相对偏差为−30%，小部分计算值大于测量值，且计算值与测量值比较接近。

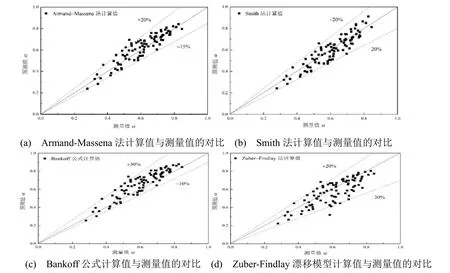
图6 4 个理论公式计算值与伽马射线测量值的对比

通过比较，Armand-Massena法计算值与伽马射线测量值较为相近，预测效果最好，Smith法在低含气率时预测值与试验值接近，但在高含气率时没有Armand-Massena法预测效果好，Bankoff公式计算值普遍比测量值大，且相对偏差较大，Zuber-Findlay漂移模型多数计算值比测量值小，且与测量值偏差较大。

分析产生这种结果的主要原因是：

1）本文试验中的截面含气率在0.25～0.85范围内，这与Armand-Massena公式的适用条件基本一致，因而误差较小。

2）Smith模型假设管壁处为单相水膜，管子中间为均相混合物。Bankoff模型假设气泡悬浮于液体中，适用于泡状流和雾状流。本文试验的管内流型多为泡状流过渡到弹状流，再继续演变为弹状流、块状流和带纤维的环状流，气相更多的集聚在管子中心部分。所以本文试验中Smith模型和Bankoff模型和没有Armand-Massena法预测效果好。

3）Zuber-Findlay漂移模型适用于ωJg≥0.05ω0的泡状流、弹状流、乳状流，精度较高，所以C0和ωJg应结合流型来确定，精度比较高。

4 结论

本文分析了伽马射线法对常温常压气-水两相截面含气率随折算气速、体积含气率的变化，并把测量值与经验公式及理论模型的预测值进行对比分析，得到以下结论：

1）截面含气率受折算气速和折算液速的影响较大。同一折算水速下，在低折算气速时，截面含气率主要受气速影响，且随着气速的增大而显著增大；当折算气速大于某一值时，截面含气率随着气速的增加而缓慢增加。同一折算气速时，截面含气率随着折算水速的增大而减小，且折算水速之间相差越大，变化越明显。

2）同一折算水速下，在β＜0.9时，截面含气率与体积含气率近似呈线性增长；在β＞0.9时，截面含气率随着体积含气率的增大而显著增大。

3）通过把伽马射线法测量的截面含气率与理论公式计算值对比，测量值与Armand-Massena公式计算值吻合最好，Smith法计算值在低含气率时与试验值接近， 在高含气率时没有Armand-Massena法预测效果好，多数测量值都偏小于Bankoff公式计算值，而偏大于Zuber-Findlay漂移模型的计算值，特别是Zuber-Findlay漂移模型计算值与测量值偏差较大。