谐波注入脉宽调制的有源电力滤波器

胥 良, 崔兆一

(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)

0 引 言

目前,供电系统中存在较多以电力电子装置为代表的非线性负载,会产生大量谐波与无功对供电系统造成严重污染,干扰供电系统正常运行造成经济损失,同时也会降低用电设备使用寿命,因此采取补偿装置进行无功补偿与谐波抑制变得尤为迫切[1]。有源电力滤波器(APF)是一种常见用于抑制谐波、无功补偿的电力电子装置[2]。使用空间矢量脉宽调制(SVPWM)技术的APF具有输出电流谐波含量低等优势,但SVPWM仍具有一些缺点,Clark或反Park变换会增加计算量,扇区判断和求解矢量调节时间过程复杂,不利于高精度控制。通过简单四则运算代替复杂三角函数运算无法减少调制过程[3]。笔者提出一种有源电力滤波器的简单调制方法,引入调制函数,通过调制因子求解调制函数,利用调制函数进行脉宽调制过程,分析不同调制指数下系统状态,调制过程比SVPWM更简单。

1 基本电路

APF电路模型由主电路与控制电路构成,如图1所示。主电路中根据基尔霍夫电压定律知,APF在abc三相静止坐标系下方程为

(1)

图1 APF电路模型

控制电路中改进型ip-iq省去坐标变换、平均值滤波代替低通滤波器,检测精度提高、延迟时间缩短[4]。电流跟踪引入PI解耦控制,跟踪效果增强,通过调制器对主电路控制使系统响应。

根据abc/dq坐标变换原理,式(1)变换后可得d、q旋转坐标系下方程为

(2)

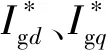
(3)

由式(3)可知,引入电流状态反馈能实现对d轴、q轴电流分别控制。若加入电压前馈补偿即d、q轴输入侧电压分量会使系统动态性能加强,实际解耦通过引入大小同耦合分量相等,方向相反分量实现电流解耦控制[5]。

2 调制方法

2.1 SVPWM技术

空间矢量脉宽调制策略有易于数字化实现等优势。根据平均值等效原理及平行四边形法则,一个周期内两个不同电压矢量与零矢量组合成参考电压矢量。在调制过程中开关顺序选取应遵循动态变换最小原则。图2a五段式SVPWM矢量作用顺序为U6(110)→U4(100)→U0(000)→U4(100)→U6(110),一个周期开关切换4次,1/3周期不动作,可降低开关损耗。图2b七段式SVPWM的矢量作用的顺序为U7(111)→U6(110)→U4(100)→U0(000)→U4(100)→U6(110)→U7(111),一个周期开关切换6次,开关切换频率提高,输出波形谐波含量低。低谐波含量输出的七段式更适合APF。软件实现空间矢量脉宽调制策略是通过定时计数器与比较器比较,实现各矢量切换[6]。比较器CMPR1、CMPR2和CMPR3的赋值如表1所示。

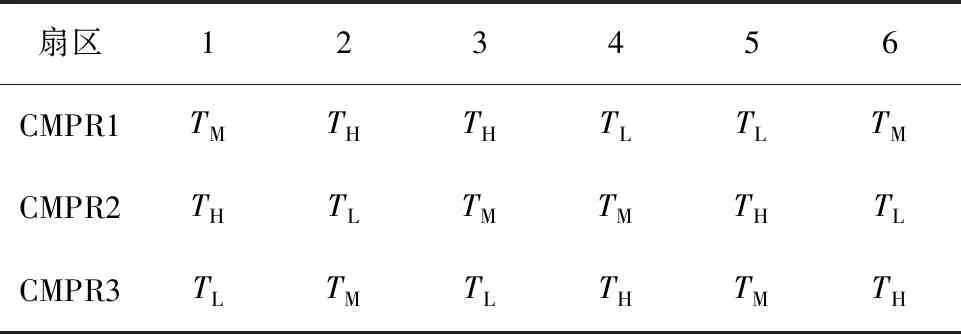
表1 比较器赋值

图2 开关顺序

采样内脉冲序列间隔会影响空间矢量调制器作用效果,在转换开关顺序中每次变化代表只采取一次行动,从状态到需求转变开关动作至少有一个间隔,若进行变化至少需要三个切换动作。它说明了空间矢量调制在一个采样区间内开关模式对开关动作的影响,开关动作越少,开关损耗越小。任意两个连续空间向量之间转换最优开关模式只需要一个开关动作。第一扇区矢量作用时间及切换过程见图3。

图3 第一扇区SVPWM开关状态和矢量切换

Sa、Sb、Sc为开关状态,TH、TM、TL是CMPR1、CMPR2、CMPR3依次递减的比较器数值分别为T0/4+Tx/2+Ty/2、T0/4+Tx/2、T0/4,TPWM为周期时间,T0、Tx、Ty是零矢量与合成矢量时间,Udc、U是直流电容电压、输入电压。根据比较器不同状态值调整后SVPWM 产生三相调制波如图4所示。

图4 SVPWM三相调制波几何分析

2.2 鞍形调制波

在调制过程中,当调制波双包络线关于水平坐标对称时可获得最理想输出效果,鞍形调制波是在优化过程中发现的一种具有清晰几何、物理意义简单调制方法[7-8]。鞍形调制波法即谐波注入法,正弦波中加入一定比例零序分量,调制信号呈鞍形,幅值明显降低,调制信号幅值不超过载波幅值,基波幅值超过三角波幅值,直流电压利用率提高,三相系统无中线时三次谐波电流无通路,线电压线电流均不含三次谐波,调制深度小且在各载波频域中存在数量更多差频波,差频波幅值较小干扰系统输出状态,导致系统总谐波(THD)含量降低,减小与谐波电流相关的转矩脉动,同时鞍形调制波可通过傅里叶级数展开论证与输入电压间的关系,在调制过程中省去了坐标变换、有效矢量作用时间计算等过程,减小了计算量,实现简单。

周期内单相鞍形调制波如图5所示。根据严格对称性知一个周期内函数:

图5 单相鞍形调制波

在一个周期[0, π]中对单相鞍形波函数进行奇延拓后傅里叶级数关系式为

(4)

f3=sin(3(2n-1)ωt)。

鞍形调制波通过基波三倍频率调制,同三相调制波相位同步幅值保持比例关系。为实现对鞍形调制波在三相逆变器中控制,可叠加输入电压,忽略环路高频成分。由式(4)可知,鞍形调制波基波外的调制波频率为基波三倍频f3,观察式(4)若调制过程可合成f3仿真易实现,则可实现一种简单调制方法,调制因子和调制函数如图6所示。当ωt∈[0,2π]时调制函数λ(ωt)由六部分相似f3的λ1(ωt)～λ6(ωt)构成,周期为π/3。λ1(ωt)在ωt∈[0,π/3] 区间内可由σc(ωt)和τb(ωt)计算,σc(ωt)、τb(ωt)是调制因子,两个调制因子σ(ωt)和τ(ωt)均由a、b、c三部分构成。当ωt∈[π/3,2π]区间时,λ2(ωt)～λ6(ωt)可由调制因子σa(ωt)、σb(ωt)、σc(ωt)、τb(ωt)、τc(ωt)、τa(ωt)、计算,最后调制函数λ1(ωt)可通过调制因子σc(ωt)、σa(ωt)和τb(ωt)求解,简化后为式(5),傅里叶级数展开后为式(6),与式(4)中谐波的级数相似。当调制比为1时,调制波接近理想状态,调制指数为0.5[8]。

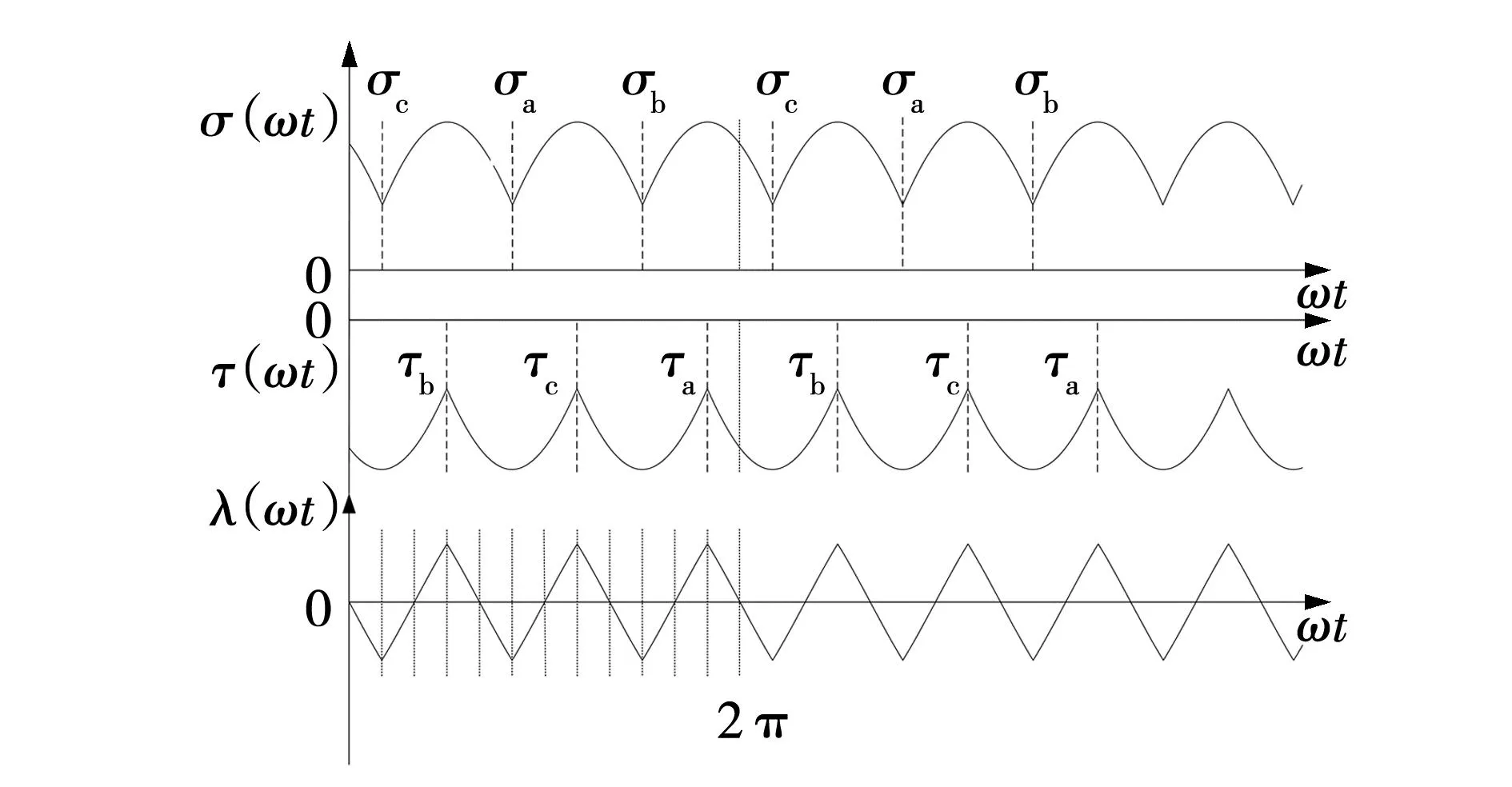
图6 调制因子和调制函数

(5)

λ1(ωt)进行傅里叶级数展开后的正弦级数为

(6)

鞍形调制波基波分量幅值提高意味着直流母线电压利用率提高,降低直流输出电压[9]。在实时运算时,鞍形调制波仅含基波三倍频谐波即零序分量,可直接调用λ1(ωt)～λ6(ωt)进行求解。通过调制函数λ(ωt) 输出可作为时基计数寄存器和比较值寄存器参考数值,加载后获得桥式结构各相上下桥臂驱动脉冲信号,各相上下桥臂脉冲信号存在一定死区且对称互补,死区信号保证各相上下桥臂不直通,确保桥式结构稳定工作,死区信号对功率开关管影响至关重要[10]。鞍形调制波调制过程节略SVPWM调制时矢量顺序比较、矢量有效时刻求解与功率开关管动作期间切换计算过程,极大简化计算程序减少数字控制时间,实现相同控制器下控制频率和控制性能的提高。三相鞍形调制波原理如图7所示。对输入侧电压Ua、Ub、Uc采样,调制因子σi(ωt)、τi(ωt)通过比较器后与调制指数ki乘法运算生成调制函数λ(ωt),调制函数λ(ωt)与输入侧电压叠加产生三相鞍形调制波,三路触发脉冲pluseA、pluseB、pluseC驱动主电路开关动作, 过程中形成的三相鞍形调制波波形如图8所示。

图7 三相鞍形调制波原理

图8 三相鞍形调制波波形

3 仿真实验与波形分析

通过Matlab/Simulink搭建APF仿真系统,仿真如图9所示。输入线电压为380 V,滤波的电感分别为2、0.2 mH,整流后非线性负载设定为阻感性,其电阻6 Ω、电感2 mH,直流侧电容容值5 mF 耐压值设定700 V,仿真时间6×10-6s。在鞍形波调制过程中给定调制指数范围0.1～1,在图10中对不同调制指数作用结果进行FFT分析和相位对比,当调制指数为0.5时调制波波形效果最好。

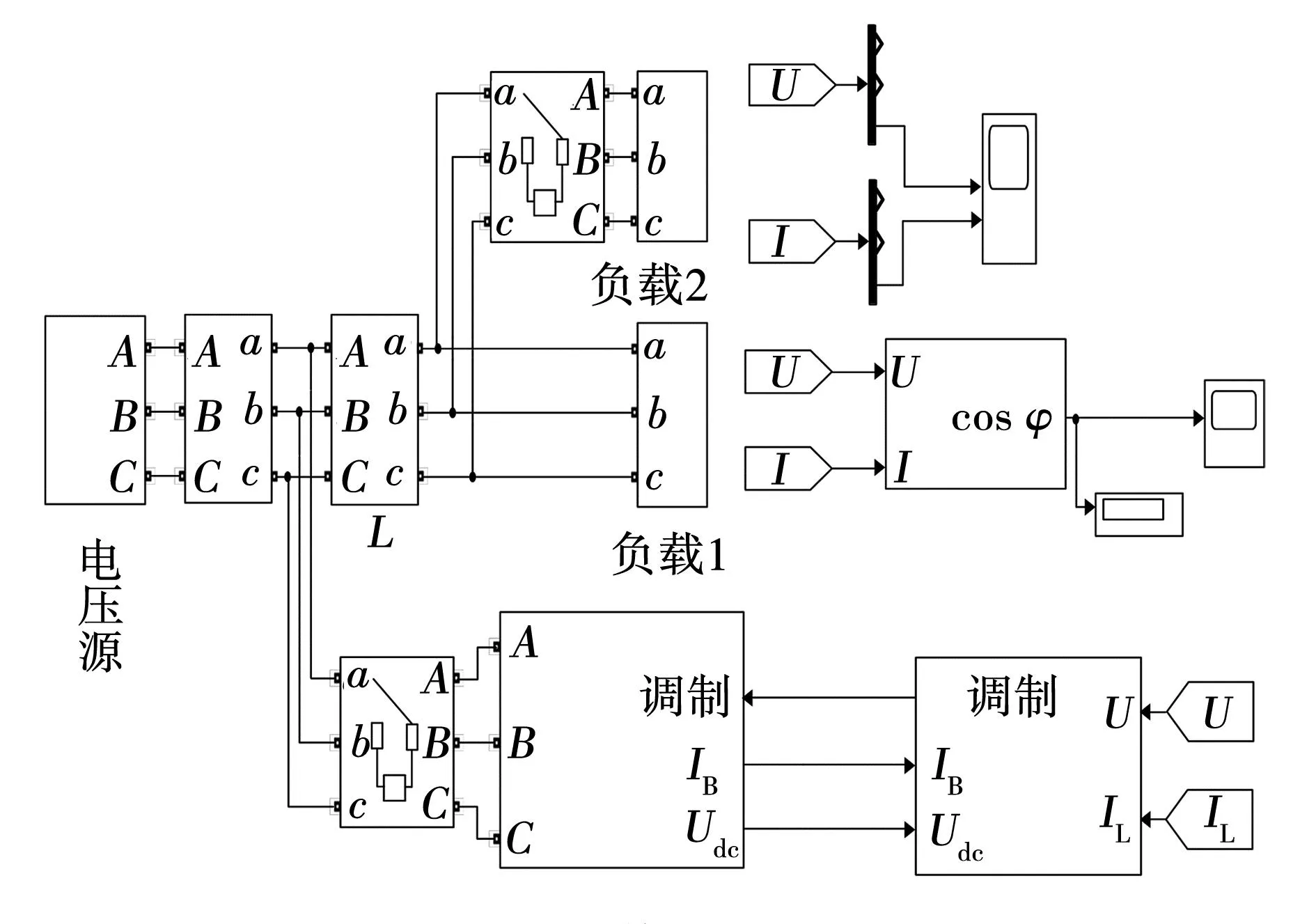
图9 系统仿真

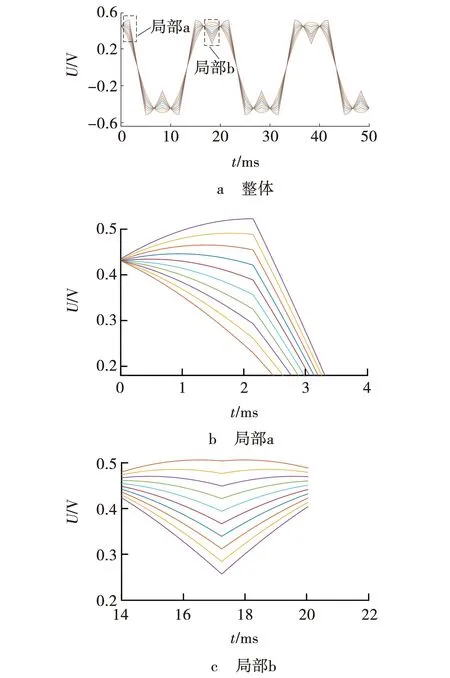
图10 不同调制指数的调制波

为了进一步验证调制指数为0.5时APF的作用效果,对电路负载进行设计,使输入电流畸变、输入电流和电压间存在相位差,仿真结果如图11～13所示。由图11a可知,在0.1 s有源电力滤波器未投入前输入c相电流与电压不同步且畸变,在0.1 s有源电力滤波器投入后输入电流仍有畸变但相位补偿后与输入电压同步。由图11b可见,在0.1 s有源电力滤波器未投入前输入c相电流畸变且与电压不同步,0.1 s有源电力滤波器投入后输入c相电流与电压仍不同步但电流谐波被抑制,电流波形改善为正弦波。由图11c可见,在0.05 s有源电力滤波器投入后输入c相电流为正弦波且与电压相位同步,0.15 s时改变负载,系统仍然稳定,有一定的动态响应。图12a为未抑制谐波时电流谐波含量,有源电力滤波器投入前后输入电流谐波含量不变为13.99%。图12b为谐波抑制时电流谐波含量,在0.1 s有源电力滤波器投入电流谐波含量小于5%。

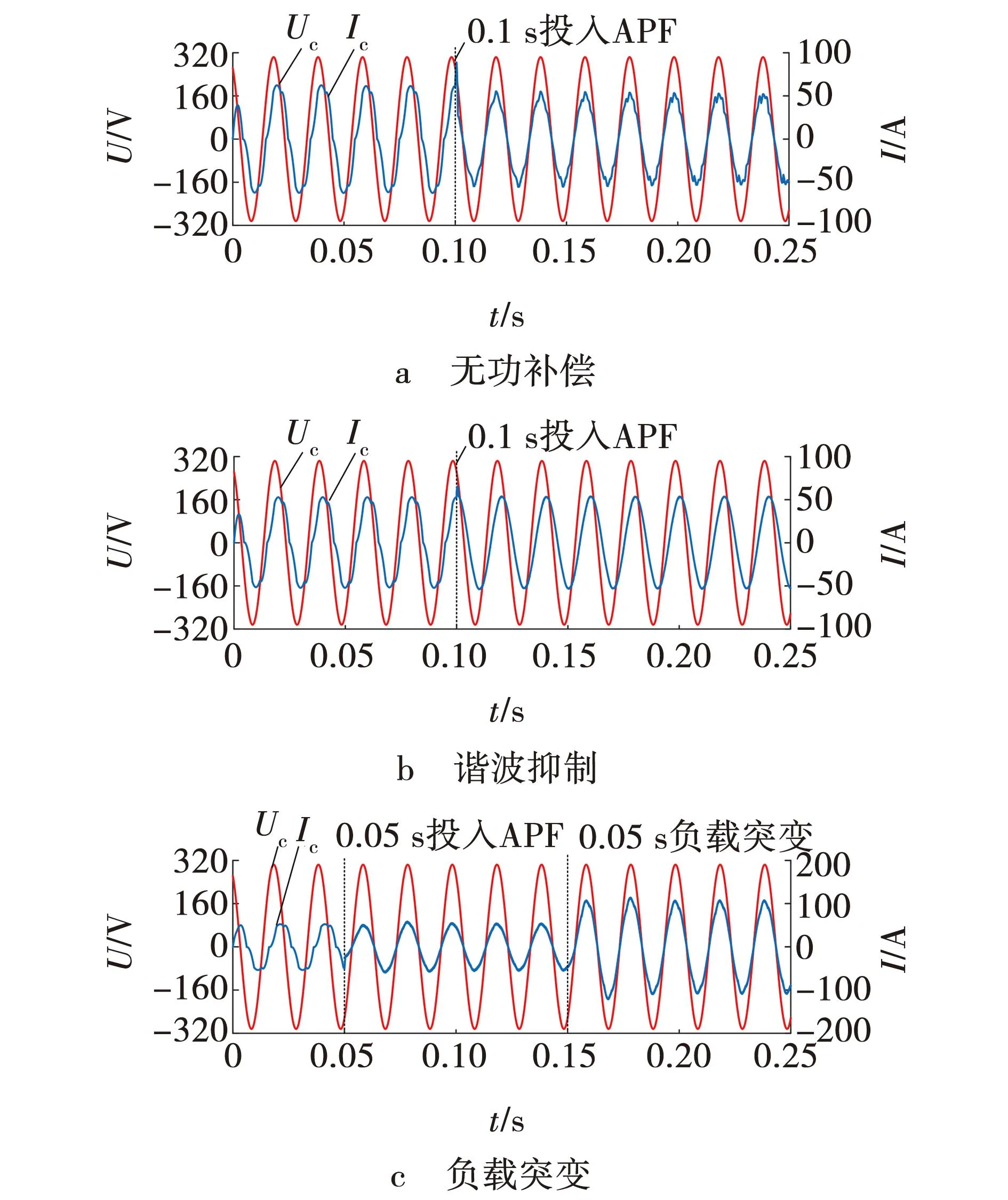
图11 输入c相电压电流

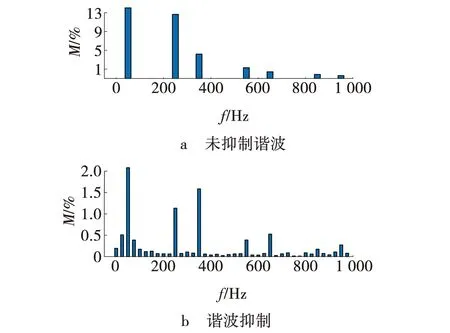
图12 输入电流THD

由图13可见,没有投入有源电力滤波器进行无功补偿时功率因数较低。投入有源电力滤波器进行无功补偿时,在0.1 s有源电力滤波器投入后功率因数提高到接近1。改变负载后,在0.05 s有源电力滤波器投入后功率因数提高到接近1,0.15 s负载突变后功率因数保持接近1不变。

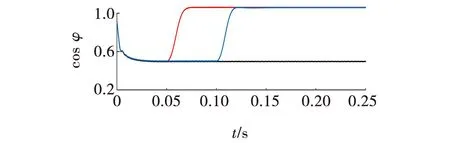
图13 功率因数

4 结 论

(1)通过分析调制过程,引入调制因子σ(ωt)和τ(ωt)求解调制函数λ(ωt)及其正弦级数,对比可知,与鞍形调制波傅里叶级数存在比例关系,当调制指数k=0.5时调制波最接近理想情况。

(2)谐波注入脉宽调制的APF在进行谐波抑制和无功补偿时都有较好的作用效果,能够降低系统谐波含量并提高功率因数,负载突变时有一定的动态响应,稳定后系统谐波含量小于5%以下,功率因数提高到接近1。