基于饱和度指标的含瓦斯水合物煤体强度预测模型

高 霞, 杨书朋, 刘 飞, 张保勇, 吴 强

(1.黑龙江科技大学 建筑工程学院, 哈尔滨 150022; 2.黑龙江科技大学 安全工程学院, 哈尔滨 150022)

0 引 言

煤与瓦斯突出是煤矿地下采掘过程中,在很短时间内从煤岩壁内部向采掘空间突然抛出大量煤与瓦斯的动力现象[1]。随着我国煤矿开采深度的增加,煤矿突出危险性日趋严重复杂,亟须建立更为适应完善的煤与瓦斯突出防治理论及技术体系[2]。吴强团队[3]提出瓦斯水合固化防突技术,初步发现水合物的存在会改变煤体力学性质,而水合物饱和度的大小是影响煤体力学性质的重要因素。因此,研究不同饱和度下含瓦斯水合物煤体力学性质及强度准则具有重要科学意义。

强度准则是煤岩力学研究的核心问题。目前,学者们对岩石的强度准则进行了大量试验研究,主要通过理论推导和试验数据拟合来建立岩石强度准则[4]。理论推导主要以经典弹塑性理论为基础,基于最大剪应力假设、最大储能假设及强度数据的最佳拟合[5];另一种常用的方法是利用已有的经典强度准则,引入参数对准则进行修正。石祥超等[6-8]基于已知试验数据对几种常规三轴岩石强度准则,进行强度模型建立与验证。韩颖等[9]基于单轴、三轴压缩试验对比研究了原煤与型煤的强度特征,引入Hoek-Brown准则,估算了煤体的强度参数。Wang等[10]对不同高度比的煤岩组合体进行了常规三轴压缩试验,分析了不同强度准则下的应力变形特征,发现Mohr-Coulomb和Hoek-Brown准则与试验结果拟合良好。Liu等[11]基于孔隙水存在的天然煤样、含水饱和煤样和渗流煤样的三轴压缩试验,以偏差绝对值之和达到最小为度量,分析了五种强度准则的适用性。以上研究成果为开展含瓦斯水合物煤体强度准则的研究奠定了基础,具有一定的参考价值。

目前,针对多孔介质水合物力学性质的研究主要集中在含水合物沉积物方面[12]。刘芳等[13]通过低温高压三轴试验研究了含水合物沉积物的强度特性,得到试样黏聚强度随水合物饱和度增加呈指数型增长。孙晓杰等[14]利用自主研制的水合物原位测量系统,研究了不同饱和度水合物沉积物岩样的力学性质,发现水合物沉积物岩样的峰值强度、内聚力随饱和度增大而增大。颜荣涛等[15]通过两种试验室方法合成含CO2水合物的砂土试样,得到两种含水合物砂土的强度和刚度随饱和度的增大而提高。王辉等[16]考虑水合物饱和度的影响,建立了基于修正Mohr-Coulomb强度准则的水合物沉积物统计损伤本构模型。张怀文等[17]引入了水合物饱和度的影响以及有效围压对水合物储层的非线性影响,建立了黏土质粉砂岩水合物储层强度准则。水合物的存在改变了沉积物试样的应力-应变特征,试样的强度随着水合物饱和度的提高而增大[18]。以上研究发现,饱和度是影响水合物沉积物的重要因素。

基于上述讨论发现,针对不同种类煤岩,其强度准则主要有Mohr-Coulomb准则、Hoek-Brown准则、广义Hoek-Brown准则、指数强度准则、Rocker准则、Drucker-Prager准则等。此外,目前鲜有考虑饱和度的含瓦斯水合物煤体强度预测模型。鉴于此,笔者利用已开展的不同饱和度(50%、60%、70%、80%),不同围压(4、5、6 MPa)含瓦斯水合物煤体常规三轴压缩试验结果;探讨不同饱和度下含瓦斯水合物煤体强度预测模型的适用性;同时,考虑饱和度的影响,引入相关力学参数黏聚力cs和内摩擦角φs,对Drucker-Prager准则进行修正,建立考虑饱和度的含瓦斯水合物煤体强度预测模型。研究结果可为工程实践中含瓦斯水合物煤体强度预测及瓦斯水合固化防突提供理论参考。

1 试 验

煤样选自黑龙江省七台河市桃山矿,型煤尺寸为50 mm×100 mm;试验所用瓦斯气样组分为99.9 %CH4,来自哈尔滨通达气体有限公司;蒸馏水自制。试验采用黑龙江科技大学自行研制的含瓦斯水合物煤体力学性质原位测试装置,如图1所示。其包括水合固化釜、三轴压缩荷载系统、温度控制系统、气体增压系统和数据采集系统等。该装置围压最大值可达20 MPa,轴压最大可达40 MPa,控温范围-20～60 ℃,可模拟煤体中水合物生成试验和含水合物煤体三轴压缩试验,具体的试验过程详见文献[3]。

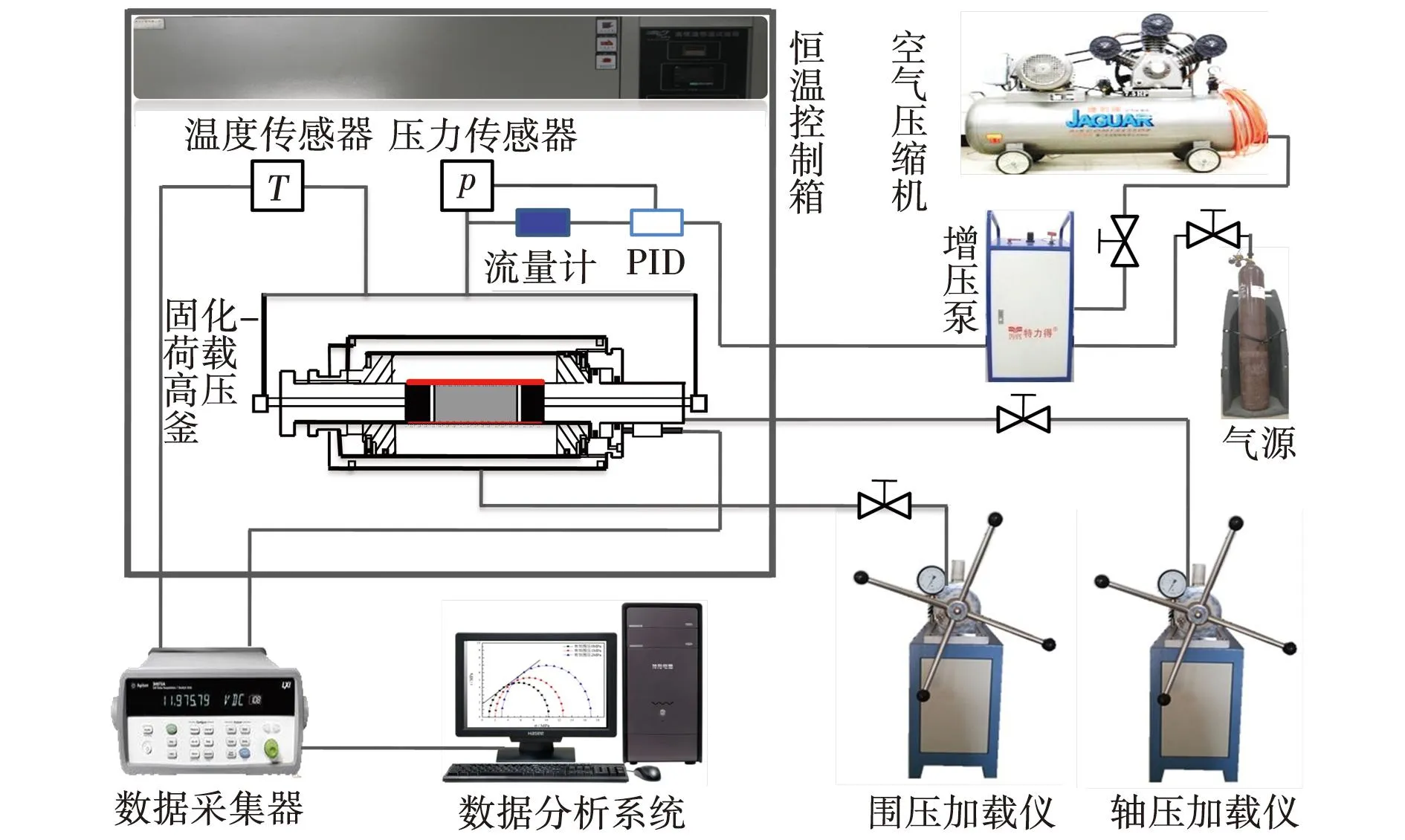
图1 含瓦斯水合物煤体力学性质原位测试装置

为了分析饱和度对含瓦斯水合物煤体强度特性的影响规律,获取峰值强度试验值,绘制不同饱和度下含瓦斯水合物煤体应力-应变曲线[19],如图2所示。

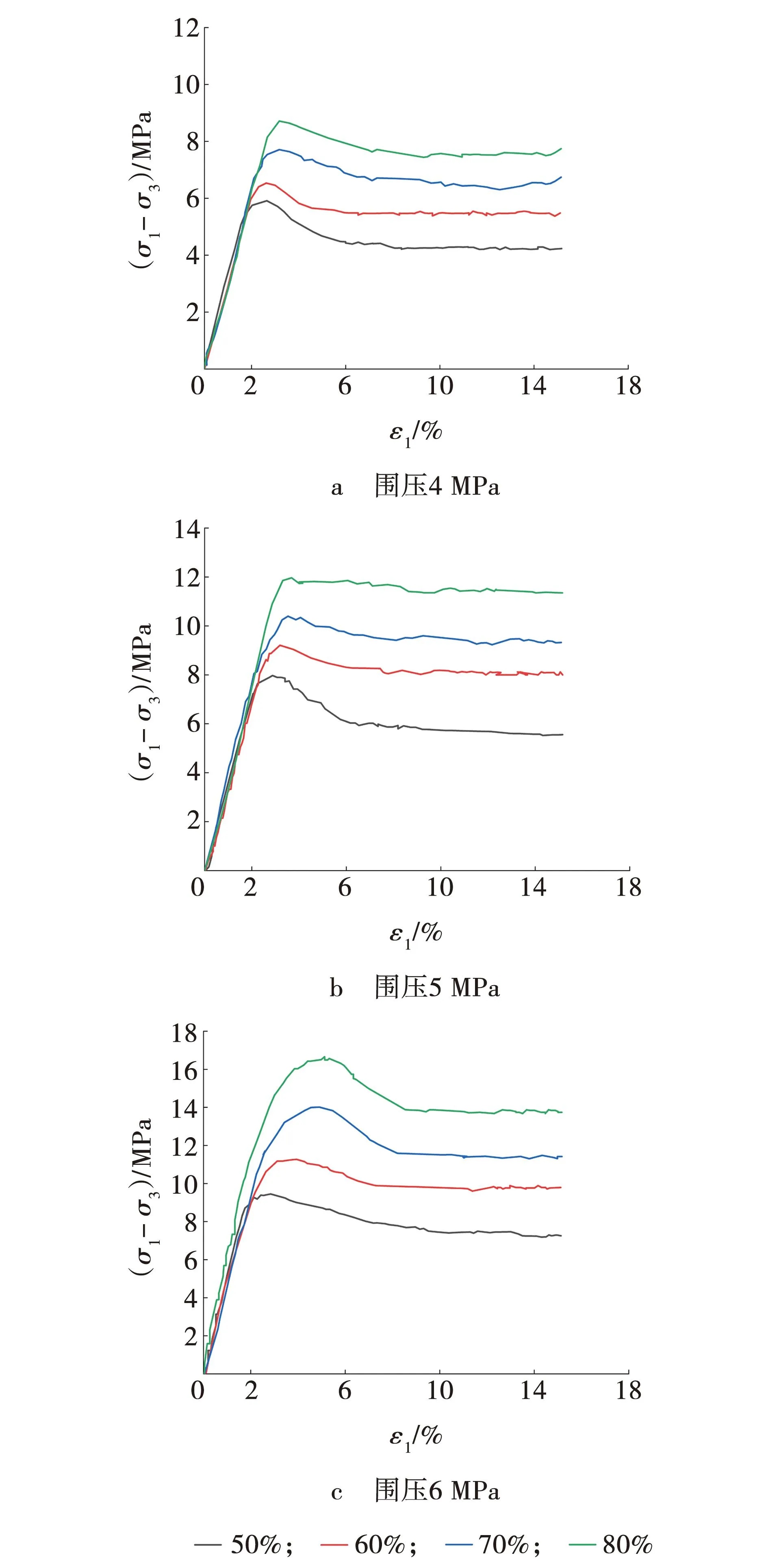
图2 不同饱和度含瓦斯水合物煤体应力-应变关系

由图2可见,不同饱和度、围压作用下含瓦斯水合物煤体应力-应变曲线形态基本一致,均呈应变软化型,全过程分为线性阶段、强化段、应变软化段、残余变形段;在同一围压下,随着饱和度的增加,含瓦斯水合物煤体应力-应变曲线整体上移,峰值强度逐渐提高;饱和度越大,水合物生成越多,含瓦斯水合物煤体内部颗粒接触越紧密,从而煤体的强度得到提高。

由上述内容可知,水合物饱和度、围压对含瓦斯水合物煤体峰值强度的影响,以便为后续含瓦斯水合物煤体强度预测模型的建立及验证提供试验依据。试验结果如表1所示。表中,Sh为饱和度,σf、σ3和σe分别为峰值强度、围压、有效围压。

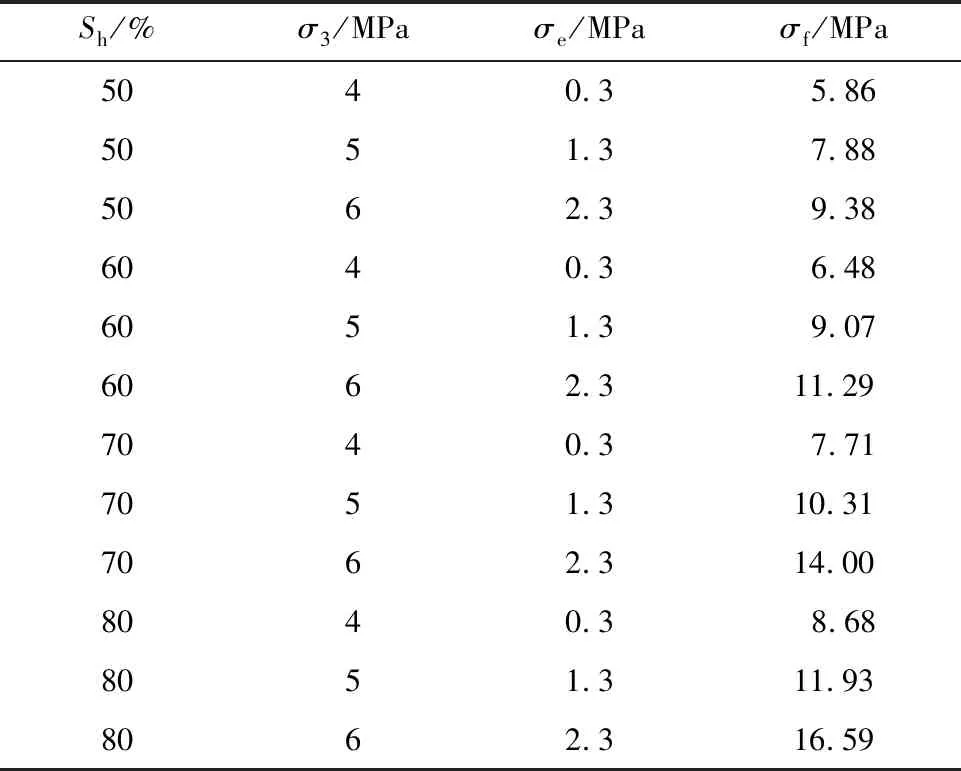
表1 含瓦斯水合物煤体三轴压缩试验结果

基于太沙基有效应力原理[20]可得有效围压,其表达式为

σp=σw-bp,

(1)

式中:σp——有效应力,MPa;

σw——外部荷载,MPa;

p——孔隙压力,MPa;

b——相关系数,其取值范围为0～1。

含瓦斯水合物煤体内部存在原生孔隙、裂隙,内部瓦斯气体造成有效围压的降低,因此文中有效围压可简述为煤体所受围压与孔隙压力之差,相关系数取1,其表达式为

(2)

式中:σe——有效围压,MPa;

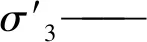
水合物生成的相平衡温压条件理论设定为(0.5 ℃,2.77 MPa)[21],在试验中,p实际值为3.7 MPa。

2 强度预测模型的构建

2.1 强度预测模型

2.1.1 指数强度准则

指数强度准则[22]是一种三参数准则,描述了岩石破坏时主应力之间存在着非线性关系,其表达式为

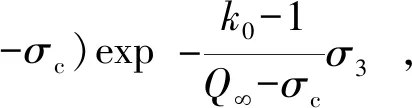
(3)

式中:Q∞——极限主应力差,MPa;

k0——围压0时强度对围压的导数值;

σc——单轴抗压强度,MPa;

σ1、σ3——试样破坏时的最大、最小主应力,MPa。

2.1.2 Rocker强度准则

Rocker强度准则[8]是基于Hoek-Brown准则而改写的三参数强度准则,其表达式为

(4)

式中:m——指数,取值范围为0.3～1.0;

Rt——单轴抗拉强度,MPa。

2.1.3 Drucker-Prager准则

Drucker-Prager准则认为材料的破坏取决于第一应力不变量和第二应力不变量,其表达式[23]为

(5)

式中:a——与内摩擦角有关的系数;

k——与内摩擦角和黏聚力有关的系数;

I1——第一应力不变量,MPa;

J2——第二应力不变量,MPa。

(6)

常规三轴压缩条件下,根据式(5)(6)可以化简为

(7)

式中,a、k——可以由内摩擦角和黏聚力表示。

(8)

2.2 强度预测模型获取思路

为获取含瓦斯水合物煤体在三轴压缩条件下的强度预测模型,利用其单轴抗压强度、峰值强度、有效围压,基于上述理论模型表达式采用数据拟合获得。文献[24]认为含瓦斯水合物煤体满足Mohr-Coulomb准则,根据准则计算含瓦斯水合物煤体的单轴抗压强度、黏聚力c和内摩擦角φ,结果如表2所示。强度计算表达式为

(9)

表2 不同饱和度下含瓦斯水合物煤体强度参数

根据单轴抗压强度以及有效围压和峰值强度进行非线性拟合,获得不同饱和度下指数、Rocker强度预测模型表达式。常规三轴条件下Drucker-Prager强度预测模型表达式由内摩擦角和黏聚力结合式(7)、(8)理论推导获得。指数强度预测模型表达式为

(10)

Rocker强度预测模型表达式为

(11)

Drucker-Prager强度预测模型表达式为

(12)

3 强度预测模型适用性分析

3.1 强度预测模型评估标准

为探究含瓦斯水合物煤体强度预测模型的适用性,选出最优强度预测模型,强度预测值的精度评估是关键环节。目前,常见的精度评价指标有平均拟合偏差、最小平均标准拟合差、回归系数、绝对误差及相对误差等。文中选择回归系数(R2)和相对误差(eRE)作为强度预测模型预测精度的评估标准[25],表达式为

(13)

(14)

(15)

式中:σ1j、σ2j、σ3j——强度试验值、预测值、统计平均值;

N——试验组数。

由上述分析可知,随着峰值强度预测值准确度的逐渐升高,回归系数R2越接近于1,eARE值越接近于0。

3.2 基于峰值强度的强度预测模型验证

为验证强度预测模型的适用性,获取强度预测模型峰值强度预测值(σy)与试验值(σf)的相关性。将不同饱和度和围压下的含瓦斯水合物煤体三轴试验结果代入式(10)～(12),得到对应的峰值强度预测值,见表3。

表3 不同强度预测模型峰值强度预测值

以峰值强度试验值和预测值为预测点(σf,σy),绘制不同饱和度、不同强度预测模型峰值强度预测值与试验值的对比图,如图3所示。选用浅洋红色对绝对误差0.5 MPa区间进行标记,蓝色短点线为预测值与试验值1∶1梯度线,红色短点线为预测点线性拟合曲线。

由图3可知,饱和度在50%、60%条件下,指数强度模型预测点在绝对误差0.5 MPa区域内,较为紧密地分布在1∶1梯度线附近,说明峰值强度预测值较为准确;饱和度在70%、80%条件下,指数强度模型预测点偏离绝对误差0.5 MPa区域,基本在1∶1梯度线下方离散分布,峰值强度预测值较试验值偏低;根据整体趋势分析,预测点拟合方程为y=0.60x+3.18,回归系数R2= 0.897,预测值平均相对误差值为6.48 %。

在四种饱和度下,Rocker强度模型预测点基本在绝对误差0.5 MPa区域内,预测点比较均匀地分布在1∶1梯度线附近;预测点拟合方程y=0.94x+0.42,拟合曲线和1∶1梯度线重合度较高;预测点回归系数R2=0.985,预测值平均相对误差值为 2.48%。

四种饱和度下,Drucker-Prager强度模型预测点均在绝对误差0.5 MPa区域内,预测点更加紧密且均匀地分布在1∶1梯度线两侧;预测点拟合方程为y=x+0.02,拟合曲线和1∶1梯度线重合度更高;预测点回归系数R2= 0.994,预测值平均相对误差值为1.92 %。

综上所述,指数强度模型峰值强度预测精度较低,在含瓦斯水合物煤体中适用性较差,饱和度越大适用性越差;Drucker-Prager、Rocker强度模型峰值强度预测值和试验值具有较好的相关性,均适用于含瓦斯水合物煤体;其中Drucker-Prager强度模型适用性相对更好,能够更加准确地预测常规三轴条件下含瓦斯水合物煤体的峰值强度。

4 Drucker-Prager强度预测模型

4.1 强度预测模型建立

根据上述结果分析可知,Drucker-Prager强度预测模型更为精准地预测不同饱和度下含瓦斯水合物煤体的峰值强度。鉴于此,为预测含瓦斯水合物煤体在不同饱和度下的峰值强度,基于Drucker-Prager准则进行修正,通过引入与饱和度相关的黏聚力cs和内摩擦角φs,来描述不同饱和度下含瓦斯水合物煤体的破坏强度特征,由式(7)和式(8)得:

(16)

(17)

由式(16)可知,若以最大主应力作为含瓦斯水合物煤体的峰值强度,最小主应力作为有效围压,则考虑饱和度的含瓦斯水合物煤体强度预测模型为

σf=Esσe+Fs,

(18)

式中:σf——含瓦斯水合物煤体峰值强度,MPa;

Es、Fs——试验待定参数,与不同饱和度对应的黏聚力和内摩擦角有关。

不同饱和度下的Es和Fs的结果如图4所示。

由图4可见,根据其分布规律进行拟合,其拟合方程为

(19)

将Es和Fs的拟合式(19)代入式(18)中,得到考虑饱和度的含瓦斯水合物煤体Drucker-Prager强度预测模型,表达式为

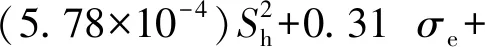
(20)

4.2 强度预测模型适用性分析

为验证修正Drucker-Prager强度预测模型的适用性,以峰值强度预测值的相对误差为评估标准,并与Drucker-Prager强度预测模型进行对比分析。

根据式(20)获得修正Drucker-Prager强度预测模型的峰值强度预测值,如表4所示。峰值强度预测值的eRE值均在6 %范围内[4],表明文中建立的考虑饱和度的含瓦斯水合物煤体强度预测模型是准确的,其eARE值为1.69 %低于Drucker-Prager强度预测模型的eARE值(1.92 %),因此,考虑饱和度的含瓦斯水合物煤体Drucker-Prager强度预测模型能够更加准确地预测含瓦斯水合物煤体峰值强度,可为计算不同饱和度下含瓦斯水合物煤体强度提供理论依据。

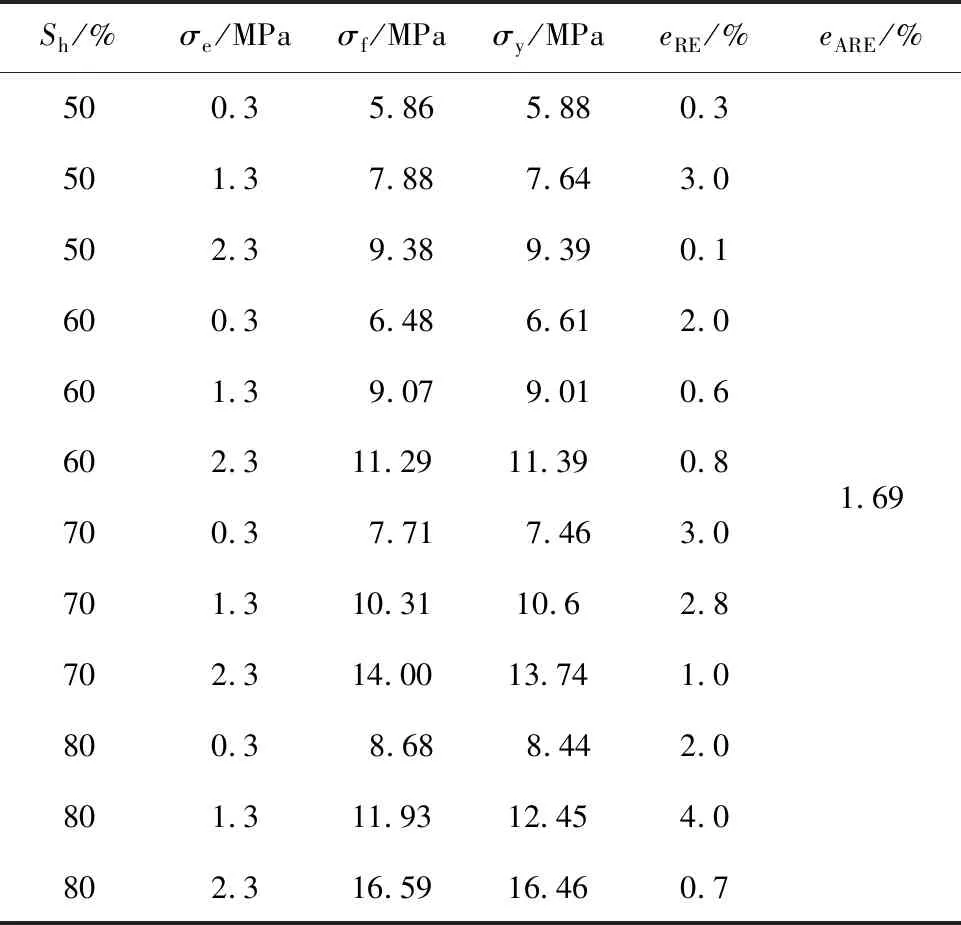
表4 修正Drucker-Prager强度预测模型峰值强度预测值

5 结 论

(1) 含瓦斯水合物煤体指数强度预测模型峰值强度预测精度随饱和度增加逐渐降低,适用性较差;Drucker-Prager、Rocker强度预测模型峰值强度预测值与试验值较为接近,预测值的回归系数均在0.98以上,模型适用性较好;Drucker-Prager强度预测模型峰值强度预测值的平均相对误差更低,预测精度更高,模型适用性更好。

(2) 通过在Drucker-Prager强度准则中引入力学参数(cs,φs),建立一种考虑饱和度的含瓦斯水合物煤体强度预测模型,该强度预测模型能够较为精准地预测含瓦斯水合物煤体峰值强度。