基于二元相关的器件级可靠性建模与剩余寿命预测研究
景博 焦晓璇 胡家兴 黄以锋 孟向臻
(1 空军工程大学航空工程学院,西安 710038;2 空军航空大学,长春 130000)
0 引言
器件作为部件及设备的主要组成部分,特别是关键核心器件,例如CPU、电源模块等,其可靠性及健康状态对设备功能完好性及任务可靠性具有重大影响[1-3]。一些器件在服役过程中,受到复杂应力的影响,通常表现出多方面的退化,例如结构裂纹扩展、电流增大、接触温度升高等[4-6]。不同性能参数之间相互影响、相互关联,基于单一性能退化的可靠性建模或忽略性能参数之间的相关关系,通常具有片面性,不能全面地评估器件的状态和退化。
当前,针对二元性能退化参数的联合建模方法主要有共同因子、相关系数和Copula 函数三种。其中共同因子和相关系数主要针对两性能参数之间的线性相关关系,能够推导出联合模型的具体数学表达式。而Copula 函数可以描述两性能参数之间的非线性相关性,并且对性能参数的边缘分布没有具体的要求,因此得到了大量的应用与研究[7-9]。Wang 等[10,11]提出了两元Wiener 过程退化模型,通过时间尺度转换将退化过程线性化,并利用FrankCopula 函数描述两性能参数之间的相关性。Zhang 等[12]利用FrankCopula 函数联合退化数据和寿命数据对卫星锂电池的寿命进行了评估。Chen 等[13]提出了利用FrankCopula 函数描述Wiener 过程和IG 过程作为边缘分布的模型。Peng等[14]提出了利用高斯Copula 函数连接两IG 过程的二元模型,并应用于重型机床。周源等[15]利用多个Copula 函数描述了继电器接触电阻和释放电压之间的关联,比较了不同Copula 函数的效果。目前,大部分的研究主要集中在特定类型的二元模型,例如Wiener 过程与Frank Copula 函数,应用具有局限性。
本文在分析了众多研究后,综合各自的特点和优点,提出基于Copula 函数的二元性能退化联合建模的流程和方法,将联合建模分解为边缘退化模型选择与确定和性能参数之间关联性的构建两部分。同时,基于卡尔曼滤波方法,提出二元性能退化的剩余寿命预测方法,并结合焊点失效试验数据进行可靠性建模和剩余寿命预测。
1 模型的建立与推导
1.1 基于Copula 函数的多性能参数可靠性建模
由于性能参数特点的不同,性能参数可能服从不同的随机过程。当前随机过程的主要形式有Wiener 过程、Gamma 过程和IG 过程。根据是否考虑随机效应和测量误差又可分为固定效应、考虑随机效应和考虑随机效应与误差的模型。假定y ij(t)表示第i个样本的第j个性能参数在t时刻的测量值,i=1,2,…N,j=1,2,…M,每个样本的测量点数为K。令
根据随机过程的定义可知,可通过增量Δy ij(t k)=t ij(t k) -t ij(t k-1)确定退化模型类型。因此多元的基于Copula 函数可靠性模型可以表示为
其中C(·)为Copula 函数,代表各性能参数的联合分布,F j(Δy ij(tk))为性能参数的边缘分布,θ cop和分别为Copula 函数参数和边缘分布参数。边缘退化模型为Wiener 过程,Gamma 过程和IG 过程,可表示为
当边缘退化模型确定后,便可推导出相应的边缘分布函数。在式(2)中通常利用几种常用的Copula 函数构建性能参数之间的相关性,例如阿基米德Copula 函数。而单个性能参数的边缘退化模型则可为式(3)中的任一随机过程模型。其中ΔΛj(tk|γj)=Λj(tk|γj) -Λj(t k-1|γj)表示时间间隔的非线性转换,用于处理性能退化过程的非线性问题,常用的形式有幂函数和对数等。基于此,便可对二元性能参数的退化过程进行描述。假如一个二元退化的边缘退化模型互不相同,分别为Wiener过程和Gamma 过程,则该模型可以表示为
其中,δ为Copula 函数系数。性能参数1 的退化模型为Wiener过程,a1,β1为漂移参数和扩散参数。性能参数2 的退化模型为Gamma 过程,a2,β2分别为形状参数和尺度参数。γ1,γ2分别为两个退化模型的时间尺度转换系数。
1.2 二元相关的可靠性建模
在多性能参数的系统中,当性能参数之间不相互独立,其系统可靠性由性能参数的联合分布决定。Copula 函数只需要通过性能参数的边缘分布便能构建联合分布,因此引入Copula 函数可以直接、灵活地建立系统联合分布函数。
假设有M个性能参数的退化系统在时刻t的性能参数为Y(t)=(Y1(t),Y2(t),…Y M(t))T,边缘可靠度为R(t)=(R1(t),R2(t),…RM(t))T,M≥ 2,则系统的可靠度满足以下两个特点
1)串联系统
2)并联系统
针对二元系统,其可靠度为
1)串联系统
2)并联系统
2 二元相关系统建模方法及流程
根据上面的推导可知,二元相关系统的可靠性建模主要包括边缘退化建模与联合分布构建。当利用式(2)建立系统联合分布函数时,其对数似然函数为
由于似然函数较为复杂,难以利用最大似然估计直接估计参数。然而,对数似然函数中的两个主要部分相互分离,因此可分别对两部分的参数进行估计。二元系统的可靠性建模可分为三步:1)边缘分布参数估计与模型选择;2)Copula 函数的参数估计与选择;3)系统模型的构建与评估。主要流程如图1 所示。

图1 二元系统可靠性建模流程Fig.1 Binary system reliability modeling process
选择合适的边缘分布对系统的可靠性建模至关重要,由于随机过程模型能够较好地描述多种不确定性,并且可结合相关物理模型,因此从几种常用的随机过程模型中选择合适的边缘退化模型。样本值的概率积分变化是Copula 参数估计中的重点和难点,需将样本值从样本空间映射到0到1 的均匀分布,通常利用边缘分布概率函数作为概率积分变换函数[16]。
2.1 模型的选择与确定
模型的选择主要包括边缘退化模型和Copula函数的选择。为了更好地描述各性能参数的边缘分布,从四种随机过程模型中进行择优选择。1)考虑随机效应和测量误差的Wiener 过程(WNME);2)考虑随机效应的Wiener 过程(WNRom);3)固定效应的Wiener 过程(WNFE);4)Gamma 过程(Gam)。为了描述性能参数退化过程中的非线性,引入时间尺度转换 Λ(t;γ)=tγ。由于线性过程为非线性的一种特例γ=1,因此备选的边缘分布如表1 所示。

表1 备选边缘分布模型Table 1 Alternative edge distribution model
2.2 贝叶斯推理
本节通过贝叶斯MCMC 方法实现边缘分布参数和Copula 函数的参数估计。首先进行边缘分布参数估计,根据贝叶斯定理,可知边缘分布参数的后验分布为
为了实现参数的推理,利用R 软件中的R2OpenBUGS 调用Open BUGS 进行后验分布推理及采样,从而实现参数的估计。
2.3 可靠度计算
二元相关系统的可靠度计算较一元退化系统和独立系统复杂。文献[17-20]中都涉及到二元相关模型的可靠度计算,共有两种计算方法。
1)利用边缘退化模型在时刻t的可靠度R1(t)和R2(t)作为Copula 函数C(u,v)的输入进行计算。
2)利用二元相关模型,结合蒙特卡洛方法,模拟仿真两个性能参数的退化轨迹,并统计系统可靠度。文献[20]中指出第一种方法的处理方式不正确,因为估计Copula 参数时,是利用增量的概率作为输入而非退化的值。虽然Pan 等[17]指出在扩散系数较小时这种方法可作为一种近似,但是并非所有边缘模型的扩散系统都较小,因此这种方法具有一定的局限性。本文主要利用蒙特卡洛的方法计算系统可靠度,主要有两方面的考虑。(1)该方法适用性较广,不受边缘退化模型扩散系数的约束。(2)便于计算系统可靠度,可直接根据各性能参数或产品之间的连接关系(串联或并联)进行计算,特别是在多元的情况下。
基于蒙特卡洛的二元系统可靠性计算主要分三步
1)利用Copula 函数随机生成[0,t]时间段内的样本概率点,样本点的个数一般取105。
2)利用Copula 产生的概率点,结合边缘退化模型生成各性能参数样本。
3)统计各性能参数未达到失效阈值的概率,并根据连接关系计算系统可靠度。例如,当两性能参数为串联时,计算两性能参数同时未达到失效阈值的概率,如图2 中所示两失效阈值与坐标轴形成的矩形内样本的概率,而非分别计算后再相乘。因为这两性能参数之间具有相关性,分开计算时忽略了两种性能之间的相关性。逐步分别计算不同时刻t的可靠度,便可得出二元相关系统随时间变化的可靠度曲线。如图3 所示为二元系统的实时可靠度计算流程。

图2 蒙特卡洛计算可靠度—串联计算方法Fig.2 Monte Carlo reliability calculation-series calculation

图3 二元系统实时可靠度计算流程Fig.3 Real time reliability calculation process for binary systems
2.4 剩余寿命预测
假设产品在时刻t k未发生失效,则第i(i=1,2)个性能参数的历史退化数据为Yi,1:k=(Y i(t1),Yi(t2),…,Yi(tk))T,则Yi(t k+l)-Yi(tk)与Yi(t)具有相同的形式,即当X i(t)为Wiener 过程时,Y i(t k+l) -Yi(tk)依旧为Wiener 过程;当Yi(t)为Gamma 过程时,Yi(t k+l) -Yi(t k)依旧为Gamma 过程。
当Yi(t)为Wiener 过程时,
当Yi(t)为Gamma 过程时,
即随机过程Wi(l)首次达到阈值Dk=DYi(t k)的时间。此时,二元相关系统的剩余寿命预测与初始时刻的寿命估计类似,利用更新后的实时边缘退化模型,结合系统Copula 函数计算实时可靠度曲线,再利用实时可靠度曲线估计剩余寿命。
退化模型更新时,如果边缘退化模型为Wiener 过程,可利用卡尔曼滤波算法结合状态空间模型根据监测数据对退化模型进行更新。如果边缘退化模型Gamma 过程,则利用贝叶斯方法进行更新。更新过程中,利用离线建立的退化模型作为初始条件或先验信息。
在更新退化模型并计算系统实时可靠度曲线后,便可通过下式对系统的剩余寿命进行估计
3 芯片试验数据应用
3.1 芯片可靠性建模
芯片作为电子设备的重要组成部分,其故障与失效将会导致整个电子设备功能故障。一个芯片通常由多个焊点结构组成,每个焊点结构的损伤都可能引发整个芯片的故障。为了评估芯片可靠性,试验过程中对芯片高应力区的焊点进行了监测。芯片的高应力区通过有限元仿真确定。本节利用芯片高应力区内两个焊点结构的充电时间数据进行芯片可靠性建模。首先对焊点数据进行平滑滤波,然后提取50%中位数作为特征量。试验条件为恒温75℃,正弦振动幅值为1g,频率为300Hz。如图4 所示分别为两个焊点结构的一个样本。而图4(a)为焊点结构充电时间数据提取的特征量,样本量N=4。图4(b)为两特征量增量的散点图,它们之间的相关性参数τ=0.16,表明在建模过程中应该考虑它们之间的相关性。
以该两焊点结构充电时间的特征量作为芯片的性能参数,建立芯片的二元相关可靠性模型。根据二元相关系统建模流程,采用二步法进行可靠性建模。首先,结合DIC 准则,分别选择确定两个特征量的最优边缘退化模型,并利用MCMC算法估计模型参数。然后,从备选的Copula 连接函数中选择合适Copula 函数,并估计其参数。最后,结合边缘退化模型和Copula 函数建立二元相关可靠性模型。两个特征量边缘退化模型的估计结果如表2 所示。由于充电时间的特征量不服从Gamma 过程的性质,因此只从三个Wiener 过程中选择边缘退化模型。结果显示,在三个边缘退化模型中,WNME 模型的DIC 值最小,因此选择WNME 作为两个特征量的边缘退化模型。如表3 所示为焊点结构两个特征之间Copula 函数的估计结果。从表中可知,在五个备选Copula 中,FrankCopula 函数的DIC 值最小,因此确定其作为两个特征量之间的相关性函数,这与图5(b)中显示的两个特征量之间的相关特点相符。焊点结构两个时段内特征量增量的等高线如图6 所示,图中显示两特征量增量之间的等高线形状随时间没有发生变化,而相同时间内两个特征量增量的幅值随时间增大。

表3 焊点结构的Copula 函数参数估计结果Table 3 Parameter estimation results of Copula function for solder joint structure

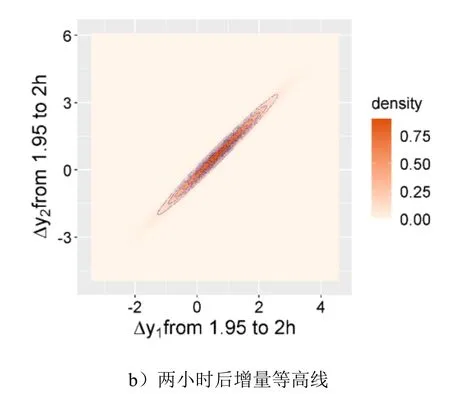
图6 两特征量增量的等高线Fig.6 Contour lines with two feature increments
假定焊点结构两个特征量的失效阈值为Df1=Df2=10ms,则根据边缘退化模型与二元相关模型,可分别计算单个特征量及两个特征量相联合的可靠度函数。如图7 所示为该芯片可靠函数,分别列出了单个特征量的可靠度函数、两特征量相互独立的可靠度函数以及基于Copula 函数的二元相可靠度函数。图中显示,同时考虑两个特征量的芯片可靠度低于只考虑单个特征量的可靠度。另外,当认为两特征量之间相互独立时会低估芯片的可靠度,因此在建模过程中,应该考虑两特征量之间的相关性。
3.2 芯片剩余寿命预测
通过对芯片进行二元相关性建模可知,两个性能参数的边缘退化模型都为WNME 模型。在剩余寿命预测的过程中,利用卡尔曼滤波结合状态空间模型对边缘模型中的参数进行更新。如图8 所示为芯片的两个性能参数退化过程,将利用该两性能参数进行剩余寿命预测。

图8 芯片的两个性能参数Fig.8 Two performance parameters of the chip
令两个性能参数的失效阈值分别为D1=7.6ms 和D2=7.7ms,如图9 所示为两个性能参数每间隔0.3h的剩余寿命预测结果。图中显示,两个性能参数的剩余寿命预测值与真实值接近,具有较好的预测结果。

图9 两特征量的剩余寿命预测Fig.9 Residual life prediction of two characteristic quantities
另外,在边缘退化模型根据实时监测参数更新后,联合Copula 函数对芯片的实时可靠度进行估计,并预测剩余寿命,如图10 所示为剩余寿命预测结果。在退化过程中,寿命预测值与真实值接近,在各个监测点略小于真实值,即低估真实寿命,但都具有较好的预测效果。同时图中也列出了两个性能参数独立时的剩余寿命预测中,通过比较可以发现,考虑两性能参数之间的相关关系时具有更好的预测效果。
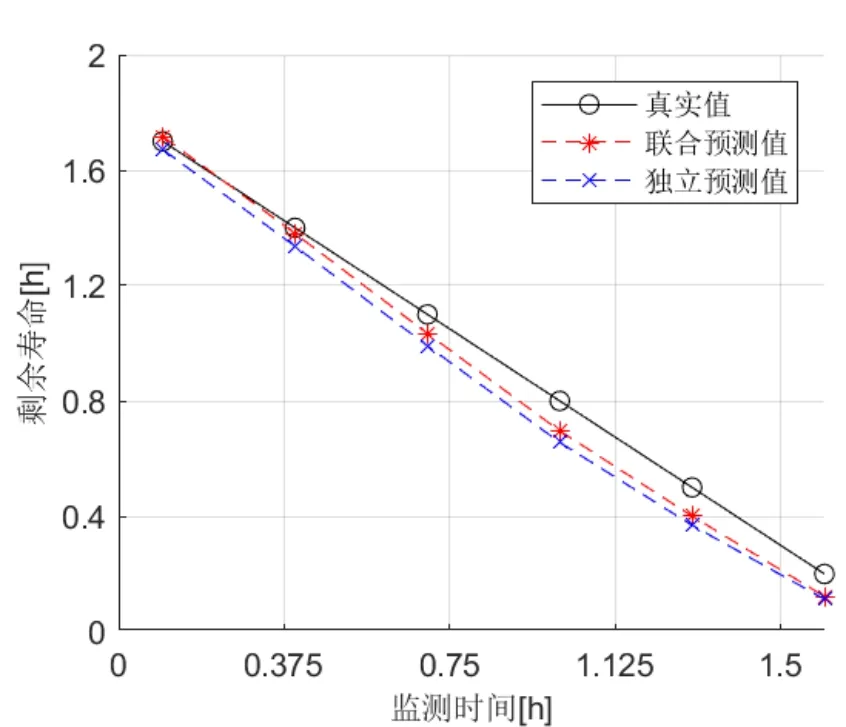
图10 芯片剩余寿命预测Fig.10 Prediction of chip remaining life
4 结论与展望
作为电子设备重要组成部分,器件可靠性对电子设备的功能完好性具有重大影响,特别是部分关键器件。本文以具有两个性能参数的芯片为研究对象,在考虑两性能参数之间相关性的基础上,建立了基于随机过程模型和Copula 函数的二元相关可靠性模型,明确了边缘退化模型和Copula 函数的选择与确定原则。同时,基于MCMC,提出了边缘退化模型参数和Copula 函数参数估计方法,并结合实时监测数据,基于边缘退化模型的在线更新,提出了二元相关的剩余寿命预测方法,主要结论如下
1)通过分别详细分析和讨论边缘退化模型及Copula 函数失配对二元相关模型的影响,结果表明,Copula 函数失配导致的偏差较大,而边缘退化模型只有在退化速率随时间下降时才会导致较大的偏差。另外,也分析了DIC 准则用于边缘退化模型和Copula 函数选择与确定的有效性。结果显示,DIC 准则能够较好地用于边缘模型和Copula 函数的选择与确定,并且随着样本量越大,效果越好。
2)利用焊点结构的充电数据对本文提出的二元相关模型进行拟合及验证,结果显示,该二元相关可靠性模型能够较好地描述两特征量之间的相关性及其随时间变化的特性。通过比较不同情况下器件可靠度函数可知,只考虑一种性能参数或认为两种性能参数相互独立都会导致器件可靠度估计时出现偏差。
3)利用一组芯片数据进行了剩余寿命预测分析,结果表明,基于Copula 函数的可靠性模型能够较好地预测芯片在退化过程中的剩余寿命。与不考虑性能参数之间相关性时相比较,考虑相关性的联合模型能更准确地预测焊点结构在各个监测点的剩余寿命。

