可重复使用运载器舵轴裂纹扩展寿命分析

蔡巧言 李配缘 黎增山 冯家赫

（1 中国运载火箭技术研究院，北京 100076；2 北京宇航系统工程研究所，北京 100076；3 北京航空航天大学，北京 100191）

0 引言

可重复使用运载器飞行全程面临复杂力学环境、宽域操稳特性、大范围不确定性散布等多约束问题。可重复使用运载器舵面传动机构使舵面产生相应的舵偏角来实现飞行姿态控制。舵轴不仅作为传递驱动装置输出的执行机构，同时承担舵面部件与机体结构的安定连接作用，对飞行安全有至关重要的影响，在设计时定义为断裂关键结构。

损伤容限设计承认结构带有初始缺陷，但必须通过设计方法将这些缺陷或损伤在规定的检修周期内控制在一定范围内，抵抗因此而产生的破坏。使用损伤容限设计思想分析此类断裂关键结构，可确定其允许的初始损伤、临界裂纹尺寸、剩余强度与裂纹尺寸的关系、确定裂纹从可检尺寸扩展到临界裂纹尺寸的周期、确定检修间隔，以支撑建立工程可用的可重复使用运载器重复使用次数评价体系[1]。

基于可靠性的耐久性/损伤容限设计是目前国内外航空飞行器寿命设计最常用的方法。美国空军主要基于耐久性/损伤容限保障飞行结构安全，美国海军受作业环境所限，采用安全寿命/损伤容限对飞机结构寿命进行监控，依靠严格的出厂检测和精细的载荷监控保障结构的安全。

在可重复使用航天器设计领域，目前SpaceX将可重复使用火箭复用检测分为三个级别：A 级检测在每次飞行任务后都要进行；B 级为定期维修，目前是在一子级执行6 至7 次任务后进行一次；C级是最彻底的维护过程，用于发射次数最多的一子级及所有执行载人任务的一子级。

SpaceX 的技术人员针对评估具有复杂几何形状的大型复合材料空间结构还提出了一种实用损伤容限方法[2]，由三个要素组成

1）使用经试验验证的分析技术确定可接受的缺陷尺寸，同时确保这些缺陷大于与所选无损评估（NDE）技术相对应的最小可检测缺陷尺寸；

2）实施验证测试程序，以验证工艺；

3）使用严格的接受/拒绝标准进行预验证和后验证无损评估。

对于裂纹扩展的有限元仿真，目前广泛应用扩展有限元（XFEM）法[3]。扩展有限元法在计算过程中，不连续场的描述完全独立于网格边界，故广泛应用于处理裂纹、空隙、界面层等不连续问题。与传统有限元相比，该方法所使用的网格与结构内部的几何或物理界面无关，从而克服了在诸如裂纹尖端等高应力和变形集中区进行高密度网格剖分所带来的困难，模拟裂纹生长路径时也无需对网格进行重新剖分，大大降低了计算成本。Gairola.S等[4]使用扩展有限元法对合金内部拉伸断裂的行为进行模拟，计算了不同工况中的应力强度因子和J 积分，并得知在分析断裂韧性问题时，三维有限元模型的仿真结果更好。Bashir.R 等[5]结合Von Mises 准则分析了I型裂纹尖端附近的应力场，并对裂纹扩展方向进行了预测。C.Duan 等[6]研究了涡轮合金材料在不同温度下的断裂行为，计算了不同温度下裂纹尖端处的应力强度因子，并求解了扩展的有限元裂纹长度，得到了疲劳裂纹扩展速率da/dN曲线。Nur Azam Abdullah 等[7]和 R.Rashnooie 等[8]分别基于XFEM 法对复合材料层合板的层内及层间破坏和复合材料-金属粘接面损伤行为进行评估及疲劳寿命预测。

目前，对于30CrMnSiA 钢，已有针对多种特定结构形式和载荷输入下的损伤容限分析研究工作，但对于文中研究对象，预置微小裂纹的板件在中高载下的裂纹低周扩展特性尚无系统性研究。谢伟等[9]探究缺口尺寸对30CrMnSiA 低周疲劳寿命的影响，利用简化的M-C 公式来评估材料的低周疲劳寿命。陈水根[10]对某型飞机采用30CrMnSiA的主起落架接头进行损伤容限分析，确定其检修周期。但对于0Cr17Ni4Cu4Nb 不锈钢（17-4PH），目前多是研究材料的细观特征、加工工艺、化学组分对力学性能及抗腐蚀性能的影响[11-12]。

可重复使用运载器的飞行环境严苛复杂，对于结构损伤的分析工作较为缺乏，亟需对于舵轴等控制舵面传动结构的寿命做出评价以满足运载器的飞行安全、检测维护与可重复使用性评估。本文针对可重复使用运载器中应用的 30CrMnSiA 及0Cr17Ni4Cu4Nb 两种典型材料，通过一种基于预置平面穿透裂纹试验件的损伤容限试验，获得拉-拉载荷下裂纹扩展长度随加载次数的变化关系，通过后续数据分析处理，获得材料的裂纹扩展参数。通过建立针对该类试验件断裂仿真的有限元分析方法，分析一种含有预置裂纹的过盈配合的键-键槽连接结构的裂纹扩展特性，对其使用寿命进行预测。

1 含预置裂纹金属板件疲劳裂纹扩展试验

1.1 试件

试验件几何特征如图2 所示，一个宽度为h的有限宽度的平板，板在远离裂纹的两端受均匀的单向拉应力σ作用。板的正中心位置有一半径为r的双边开裂孔，孔两侧沿宽度方向有一条长度为2a的预置裂纹，预置裂纹采用线切割加工，宽度0.2 毫米。板件的上下表面粗糙度为Ra0.8，无其余划痕与锈蚀。

表1 含预置裂纹的板件几何尺寸Table 1 Geometric dimension of plates with pre-set cracks

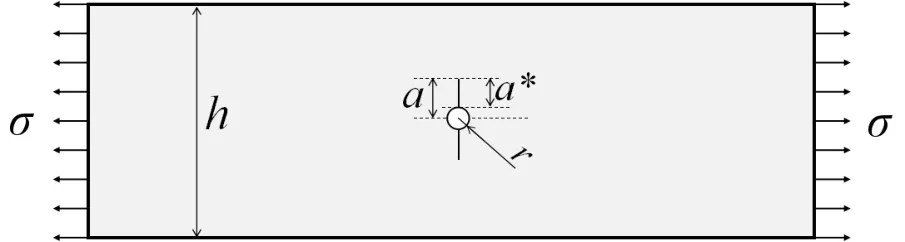
图2 受平面拉伸的含预置裂纹的板件Fig.2 Plate with pre-set cracks subjected to plane tension

1.2 试验方法

本次试验使用美国MTS 公司的MTS-370 型50 吨液压静力-疲劳试验机进行加载。该试验机精度为1 级，最大量程为500kN，如图3 所示。

图3 静力-疲劳试验机Fig.3 Static-fatigue testing machine

试验前按GB/T 228.1[14]测试30CrMnSiA 及0Cr17Ni4Cu4Nb 两种材料的抗拉强度σ b、σ0.2和δ5，每种不少于3 个有效数据，计算其平均值。

试验开始时测量初始裂纹长度及试验件几何尺寸，然后每隔1000 次数循环测量一次裂纹长度，直至断裂，记录试验信息、断裂部位、不同循环次数对应的裂纹长度。统计分析试验数据，绘制a～N曲线、da/dN～ΔK曲线等。其它试验要求按GB/T 6398[15]。加载时要求试件的横截面形心与试验机加载中心重合，沿着试验件轴向加载，避免试件扭转。加载方案如表2 所示。

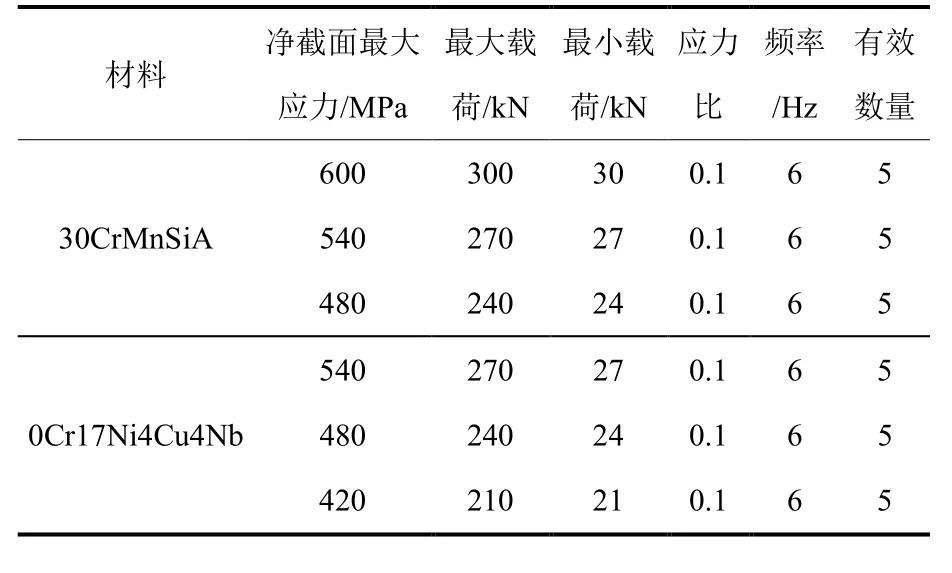
表2 试验方案信息Table 2 Test information

1.3 试验结果

两种材料疲劳破坏模式为预置裂纹在加载下向横向两端延展，板件结构剩余强度降低，当板件不足以承载时发生突然断裂。板破坏在不同应力水平下的各组试样的a-N曲线如图5 和图6 所示。总的看来，各个试验件的预置裂纹随着加载次数增大均经历了缓慢扩展到快速扩展直至突然断裂的过程，并且随着加载次数增大，同种工况下的试验结果分散性也逐渐增大。同种材料在不同应力水平下，载荷越大，曲线斜率da/dN不断增大，即试样疲劳裂纹扩展速率越快，试件的疲劳寿命也越小；由于试件强度一定，相应的板件断裂的临界裂纹尺寸也越小，临界裂纹尺寸长度可由试验结果外推估算。在同等应力（540MPa，480MPa）水平下，30CrMnSiA 及0Cr17Ni4Cu4Nb 两种材料的疲劳裂纹扩展水平相当、且寿命接近。加载次数较低时，同种材料的试件裂纹长度无明显差异，随着加载次数增大，裂纹长度的分散性开始增大。当裂纹长度扩展至约10 毫米时，裂纹扩展速率显著增大，当裂纹扩展到25 毫米至30 毫米水平时，由于剩余性能不足以承受拉载，发生突然断裂。

图4 试验过程中拍摄的裂纹扩展Fig.4 Crack growth photographed during the test

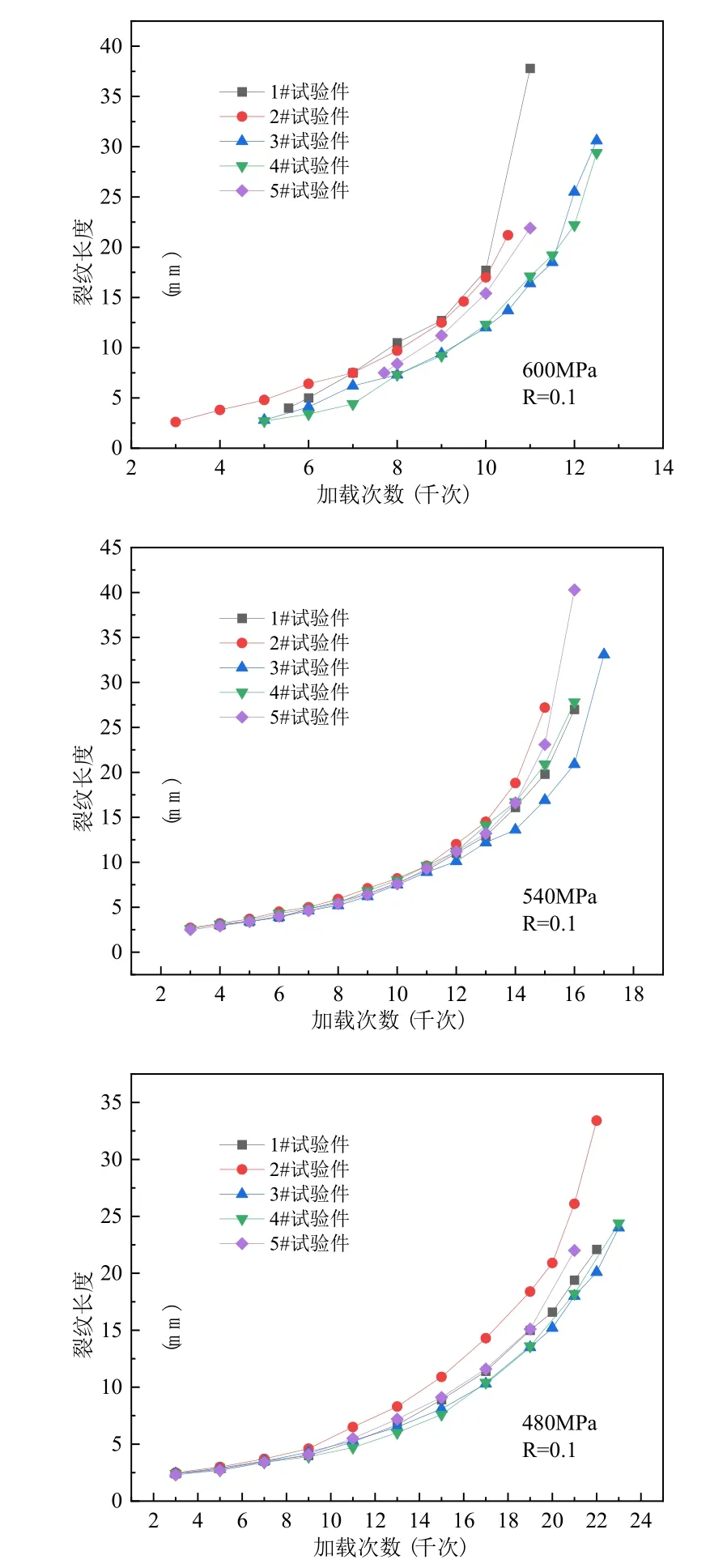
图5 30CrMnSiA 试验件在三种不同加载水平下裂纹扩展长度随加载次数变化Fig.5 Crack growth length of 30CrMnSiA test piece changes with the loadings times under three different loading levels

图6 0Cr17Ni4Cu4Nb 试验件在三种不同加载水平下裂纹扩展长度随加载次数变化Fig.6 The crack growth length of the 0Cr17Ni4Cu4Nb test piece changes with the loading times under three different loading levels

裂纹开始扩展时速率缓慢，速率变化接近线性，根据试验记录的裂纹长度-加载次数结果，将其外推至裂纹扩展0.1毫米时的加载循环次数作为裂纹起始扩展寿命，以试验件发生突然断裂时的循环加载次数作为裂纹扩展寿命，两种材料的裂纹起始扩展寿命、扩展寿命如表3。可以看出，对于同种材料，裂纹开始发生扩展的循环次数和裂纹扩展寿命均随着载荷水平的减小而增大，且随着载荷加载水平的线性下降，起始扩展次数和裂纹扩展寿命呈现出非线性的增长。对于同样载荷水平下两种材料的试验件，虽然裂纹起始扩展时对应的循环加载次数和裂纹扩展寿命在同一量级，但仍存在一定差异，总体看来在同等条件下，此类试验件中30CrMnSiA 的疲劳特性略优于0Cr17Ni4Cu4Nb。

表3 30CrMnSiA 及0Cr17Ni4Cu4Nb 试验件裂纹扩展寿命Table 3 Crack growth life of 30CrMnSiA and 0Cr17Ni4Cu4Nb test piece

2 有限元分析

2.1 材料断裂参数计算

1963 年P.C.Paris 在引入应力强度因子表征裂纹尖端应力场强度的基础上，提出裂纹扩展规律与应力强度因子的公式，以此估算裂纹疲劳扩展寿命，在此基础上发展出损伤容限设计。根据Paris公式[16]，裂纹扩展速率与ΔK之间的关系为

对于单轴远处加载的双边径向穿透裂纹开裂孔，其应力强度因子一般形式可写为[17]

式中β为应力强度因子的修正系数，与裂纹结构的几何形状有关。其值等于应力强度因子Bowie解理论值乘以修正系数a，a值可通过仿真模型中静态裂纹尖端J 积分值推出。

假设每次循环加载裂纹长度扩展值为一小量，可认为每一次循环中，应力强度因子的差值

在线弹性断裂力学范畴内，对于平面应力问题，应变能释放率G和应力强度因子K之间有如下关系式[18]

ABAQUS 中判断裂纹开始萌生的条件为[19]

故裂纹萌生开始时有如下线性关系

裂纹扩展速率与ΔG之间的关系为

此处

图7 30CrMnSiA 的da/dN-ΔG 数据点及拟合结果Fig.7 da/dN-ΔG data points and results of 30CrMnSiA

图8 0Cr17Ni4Cu4Nb 的da/dN-ΔG 数据点及拟合结果Fig.8 da/dN-ΔG data points and results of 0Cr17Ni4Cu4Nb

通过对试验数据进行整理及拟合，可得到疲劳裂纹萌生/扩展的材料常数c1到c4。

在涉及I 型、II 型和III 型损伤的一般情况下，断裂准则定义为

幂法则和B-K 法则可用来描述混合模式下裂纹起始及扩展[19]

式中，Gequiv为等效应变能释放率，GequivC为临界等效应变能释放率，GI、GII、GIII分别为I型、Ⅱ型、Ⅲ型裂纹对应的应变能释放率，GIC、GIIC、GIIIC分别为I型、Ⅱ型、Ⅲ型裂纹对应的临界应变能释放率。a m、a n、a0、η：指数。

表4 中，Gc为等效临界能量释放率，Gthresh和Gpl为Paris 公式中能量释放率阈值和上限。Gthresh/Gc和Gpl/Gc的默认值分别为0.01 和0.85[19]。

表4 材料断裂性能参数Table 4 Material fracture performance parameters

2.2 有限元计算仿真模型

根据试验件几何特征创建三维仿真模型，中间添加一条初始长度2mm 的可扩展裂纹。板件底部的边界条件为底面四边铰支（U1=U2=U3=0），加载端选用带有幅值变化的均布载荷模拟。

板件采用减缩积分，沙漏控制的八结点线性六面体单元（C3D8R）。中央裂纹富集区域加密网格，该部分网格尺寸约为1mm。

采用Direct cyclic 分析步进行低周疲劳分析，增量步步长为0.1。通过添加关键字来描述Paris公式以及相应的断裂准则。

图9 含裂纹扩展结果的有限元仿真模型Fig.9 Finite element simulation model including crack growth results

2.3 有限元仿真结果与试验结果对比

30CrMnSiA 与0Cr17Ni4Cu4Nb 试验件在不同载荷水平下裂纹扩展试验结果与伴随试验的有限元模型的仿真结果对比分别如图10 和图11 所示。

图10 30CrMnSiA 试验件裂纹扩展仿真与试验结果对比Fig.10 Comparison of crack growth simulation results and test results of 30CrMnSiA test piece

图11 0Cr17Ni4Cu4Nb 试验件裂纹扩展仿真与试验对比Fig.11 Comparison of crack growth simulation results and test results of 0Cr17Ni4Cu4Nb test piece

图12 含预置裂纹的有限元计算模型Fig.12 Finite element analysis model with pre-set cracks

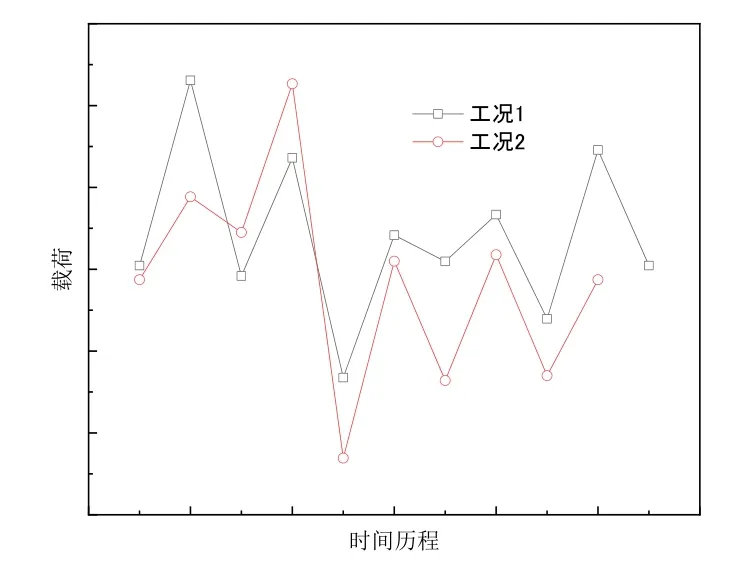
图13 单次循环中加载的载荷-时间历程Fig.13 Load-time history applied in finite element analysis

通过有限元仿真结果与试验结果对照，可见有限元仿真结果的数据点基本可以准确描述裂纹扩展的发展趋势，对裂纹扩展寿命预测良好（表5）。由于无法实时测量板件突然断裂瞬间的裂纹扩展长度，因此采用插值外推的方法根据疲劳寿命进行推算，导致因此推算的GC值较小，利用表4 中的参数仿真计算得到的疲劳寿命相对偏保守，但与试验结果平均值误差均在10%以内。

表5 裂纹扩展寿命有限元分析结果与试验结果对比Table 5 Comparison of finite element analysis results and test results of crack growth life

3 可重复使用运载器传动机构裂纹扩展分析

可重复使用运载器舵轴的伺服机构通过键连接实现对轴的运动传递。对于一处键连接的舵轴结构，键与键槽尺寸公差按GB/T 1095 规定[20]采用一般连接。在键槽内侧面与键的棱边接触的区域布置一个1mm×1mm 的预置裂纹。在轴上加载循环载荷，该载荷的一次循环考虑单次全剖面飞行过程中造成主要疲劳损伤的主波和二级波[21]的作用，得到裂纹扩展面积随着加载循环次数的变化情况，如图14 所示。

图14 裂纹扩展面积随飞行次数的变化Fig.14 Evolution of crack damage area with number of loading cycles

从有限元计算结果可以看出，虽然舵轴这类结构在设计中应采用安全寿命设计方法，但即便在损伤敏感区域出现1mm×1mm 的未被检出裂纹时，在给定设计工况载荷作用下，该类结构在15 次飞行内仍能保持该类预置裂纹缓慢扩展，在40 次飞行内仍能保持结构完整。

4 结论

本文针对可重复使用运载器中常用的30CrMnSiA 及0Cr17Ni4Cu4Nb 两种典型材料，通过一种基于预置平面穿透裂纹试验件的损伤容限试验开展了舵轴裂纹扩展寿命研究，得到以下结论

1）获得两种材料在三种应力水平下的裂纹扩展长度随拉-拉加载次数变化的结果。从结果来看，高应力水平下裂纹扩展曲线斜率da/ dN不断增大，即疲劳裂纹扩展速率增大、疲劳寿命减小；裂纹临界尺寸与载荷的平方成反比；同等应变能释放率ΔG两种材料之间的裂纹扩展速率无显著差异。

2）根据试验数据推算控制材料疲劳裂纹萌生/扩展的材料常数，修正了应力强度因子系数Bowie解，并建立伴随试验的低周疲劳有限元仿真模型。计算结果与试验结果吻合较好，能够预测其他载荷水平下裂纹的扩展特性。

3）基于以上结果建立一种含有预置裂纹的过盈配合的键连接机构的裂纹扩展预测模型，为该类连接结构完整性评估提供支撑。