能量有限元方法研究进展及其非平面波情况下的改进

于开平 王怀志

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引言

随着技术的发展，高速行驶的机车以及航空航天中高速飞行器等结构的研究都对动响应预示方法提出了更多的需求，传统振动环境预示方法，如有限元和边界元等[1]，随着频率的提高需要更高的网格密度，导致单元类的方法在中高频响应计算上效率较低，且随着频率的提高，结构的模态更加密集，有限元方法很难得到准确的结构固有频率信息[2]。统计能量分析方法（SEA）的出现可以解决有限元等方法在中高频响应计算上的一些问题[3]，基于能量在频率和空间上的平均，SEA 可以将系统简化为有限个数的子系统，简化后的模型自由度数与子系统数相关，相对于有限元方法，统计能量模型的自由度小的多，同时由于进行了空间和频率上的取平均，SEA 也适用于具有一些不确定性和随机特性的结构[4]。但是由于子系统需要满足模态密度的要求，子系统的特征尺寸一般较大，由于对结构的能量进行空间平均，SEA 无法对得到结构的局部响应信息，也无法考虑结构局部质量、刚度、阻尼和载荷等的不均匀分布问题。

能量有限元方法（EFEA）最初由Nefske[5]通过对功率流方程的研究，得到了与热传导方程类似的能量密度控制方程，该方程可以使用有限元程序进行求解。Wohlever[6]推导了杆和梁结构的能量密度方程，并对其特性进行了研究。Bouthier[7]推导了板的能量密度方程，并与有限元方法进行了比较。Bouthier[8]对板的能量有限元进行了系统的研究，并给出了无限大结构的能量密度控制方程。Bouthier[9]推导了膜结构的能量密度控制方程。Park[10]研究了基于Timoshenko 梁理论的 EFEA，HAN[11]将 Rayleigh-Love 和Rayleigh-Bishop 杆的结果与经典杆理论的结果进行了比较，Bolt[12]用EFEA 对曲梁结构进行了研究。Wang[13]考虑了热作用下板的 EFEA，Chen[14]对梁在受到预应力作用下的EFEA进行了研究，并给出了预应力作用下修正的输入功率就算公式。

EFEA 还被应用于一些复杂的结构，代文强等[15]对高速列车的车体和声腔进行了建模，综合考虑了车厢受到的轮轨激励、二系悬挂力、轮轨噪声以及气动噪声等复杂激励的作用，与实验结果进行了相比，在分析频段内仿真结果可以较好的预测车内的声压级响应，在文献[16]中，他们进一步分析了各种激励源对结构和内部声场的影响，据此对轮轨噪声进行了优化，有效的降低了车体内部的声压级。张双双[17]使用EFEA 对车内噪声进行了仿真分析。

在航空航天领域，Lima[18]使用EFEA 计算了飞机由湍流边界层激励引起的振动和内部噪声，建立了可用于EFEA 的湍流边界层载荷模型，通过对实测飞行数据的比较验证了EFEA 仿真结果的可靠性。Vlahopoulos[19]等使用EFEA 对铝制圆柱壳进行了仿真分析，该结构具有沿周向的周期性加筋和沿轴向的加筋，通过激振器在结构上施加4 个单点激励，与实际测试结果比较表明，EFEA 可以预测由加筋结构带来的周期特性，仿真结果和实测结果表现了良好的一致性，文中还比较了是否考虑加筋的周期效应对功率传输系数的影响，结果表明，如果不考虑加筋的周期效应，则传输的能量会变得更少。Vlahopoulos[20]将EFEA 应用于复合材料飞机机身结构，其中复合材料使用了等效材料建模的方式，基于耦合边界的位移协调和力平衡条件推导了复合材料层合板的耦合损耗传输系数，文中将飞机机身简化为圆柱壳结构，在10 个位置通过激振器施加单点随机激励，通过比较发现，EFEA 的仿真结果与实验结果相关性很好，误差基本满足要求。

国内对EFEA 在航空航天方面也有较为深入的应用，Xie[21]使用壳单元建立了截锥形仪器舱的EFEA 模型，并分别对仪器舱在点载荷和风洞实验提供的压力载荷作用下的声振耦合特性进行了研究。王怀志、于开平等[22]首先针对双星整流罩进行了EFEA 建模（图1），该整流罩结构具有两个声腔以及多个复合材料壳体结构，实验模拟了整流罩处于高声压级作用的情况，整流罩外表面受到混响场声激励作用，通过与实验值以及SEA 结果的比较，EFEA 在中高频段获得了良好的预示结果（图2）。然后，他们又使用EFEA 对气瓶整舱进行了详细的EFEA 建模[23]，考虑了结构受到外界混响声场激励作用下的声振耦合特性，仿真结果与SEA 的结果以及实测结果进行了对比，验证了EFEA 模型的可靠性。

图1 整流罩结构EFEA 模型及仿真结果Fig.1 EFEA model and simulation results of the fairing

图2 声腔的声压级响应Fig.2 Sound pressure level response of the acoustic cavity

此外，原凯[24]、Xie[25]对EFEA 的发展以及应用进行了总结。相对于SEA，EFEA 可以考虑更多结构的局部特征（如几何、材料属性或者阻尼等的变化），并得到结构的局部响应。相对有限元方法，EFEA 不仅具有性能上的优势，而且对于中高频分析，由于响应对结构参数变化比较敏感，有限元基于确定参数的建模往往会带来较大的误差[26-28]，基于统计的能量类方法可以较好的解决这个问题[3]。尽管EFEA 已经有了较为深入的研究，但是对于EFEA 的一些基本假设，以及计算结果的可靠性缺乏系统的总结，本文以板为例，分析了目前在EFEA 中使用的一些基本假设，并总结了目前文献中经过验证的一些可靠性评估方法，对于不满足平面波假设的情况，对一种改进方法进行了参数研究以及仿真分析。

1 能量密度的控制方程

EFEA 的能量密度控制方程基于功率流平衡，这种平衡关系可以用单元体来表示，如图3 所示。

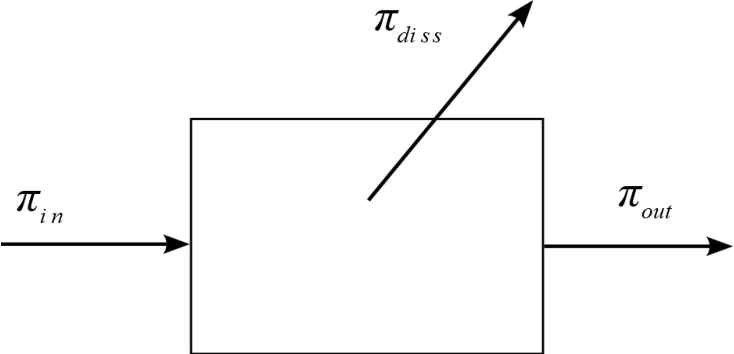
图3 单元体的能量流关系Fig.3 Energy flow relationship of unit element

这个关系可以用以下公式来表示[5]

其中E表示单元体的能量，表示单元体边界流出的能量强度，πdiss表示单元体内由于阻尼等耗散的能量，πin表示单元输出的能量。

假设系统阻尼可以简化为滞后阻尼，且阻尼足够小，则耗散的能量可以用以下公式来表述[3]

其中，η是内损耗因子，ω是圆频率。

结构中单个面波分量可以用以下公式来描述

其中，A为波的幅值，K表示波的波数，r表示距离原点的距离。

以弯曲波为例，能量密度和能量强度可以表述为

其中，D表示弯曲刚度，ρ表示密度，k1为波数K的实部。

当阻尼很小时，波数K的虚部可以忽略，则通过公式(4)可以得到能量密度和能量强度之间的关系为

其中，Cg是弯曲波对应的群速度。

将公式(5)代入公式(1)中，可以得到单弯曲面波的能量密度控制方程

仅考虑稳态振动的情况，可以去除上式中的时间微分项，则稳态的能量密度控制方程可以表述为

可以发现，从公式(1)到(7)使用面波方法的推导并不涉及具体的结构（如杆、梁和板等），这说明公式(6)和(7)适用于普遍的扩散场面波的传播过程。面波假设广泛应用于能量类方法的公式推导中[4]，EFEA 假设结构内混响场占主导，可以近似用面波来表示。

如果将考虑反射波[6]或者将结构扩展为多维结构[7]，在能量密度和能量强度的表达式中将会出现耦合项，该耦合项可以通过进行局部空间平均的方法来消除掉。所以，理论上，EFEA 与SEA类似，是需要进行空间平均的，不同的是EFEA的空间平均是局部平均，最小需要在一个波长内进行平均即可。对于杆、欧拉-伯努力梁[6]、板[7]、圆柱壳[29]、铁木辛柯梁[10]以及一阶剪切变形板[30]（单波形式）等常见结构，通用的能量密度控制方程可以表述为

其中，〈*〉表示需要对该值进行一个波长上的空间平均。而公式(5)表示的能量强度则可以重新写成为

能量密度方程可以用有限元方法进行离散，离散方法可以使用常规的EFEA，也可以使用0阶EFEA[31]。0 阶EFEA 采用了类似数值离散的集中质量方法，每个单元可以看作是一个小的SEA 子系统，该方法可以直接使用耦合损耗因子，在相同网格密度的情况下，等效刚度矩阵由于是对角阵，实际上计算量略小于传统的有限元离散方法。

公式(8)可通过Galerkin 加权余量方法来构建能量有限元方程，对于2 维板结构，余量方程为

其中N i为型函数。单元的能量可以表示为

公式(10)中的第一个积分项可以展开为

其中，

通过展开可以将公式(10)可以转化为

公式(14)可以写成以下形式

其中，

Q e表示单元边界上输入的功率流，对于结构内部（不存在几何、材料等不连续），该项可以直接消去。而对于耦合边界，需要通过耦合边界的功率流平衡关系来得到耦合传递矩阵[32]，则板的能量有限元公式可以表示为

其中，JC表示耦合边界的能量传输矩阵。

对于公式中的能量输入项Pin，一般可以通过无限大结构的原点输入导纳来得到，即

如果使用相同无限大结构的原点输入导纳计算输入功率，EFEA 的计算结果实际相当于SEA进行频率平均后的结果[3]。因为对于有限大结构，如果在一定频带内的，载荷为随机或者系统本身为随机，则其在带宽内的平均输入导纳约等于无限大板的原点输入导纳。这是EFEA 需要进行频率平均的一个原因。

2 EFEA 结果的有效性

目前，EFEA 计算结果的有效性主要可以从以下几个方面：能量耗散的计算误差，特征长度与结构内最大作用波长的比值以及直接场能量的占比。

Wohlever[6]指出，在EFEA 中，能量密度是结构动能和势能的和，而损耗的能量主要来自结构的振动，因此，公式中的能量密度实际代表的是结构动能密度的2 倍，对于结构动能和势能同相位的结构，如梁和板，在小阻尼假设下，可以近似认为动能和势能是处处相等的，但是对于杆结构，稳态振动时动能和势能具有相反的相位，所以如果杆结构内含有波长数不是半波长的整数倍，能量耗散值的计算就会引入误差。当频率比较高时，杆结构中含有的波长数增加，非整数波长引入的误差比例会逐渐降低。

Gur[33]通过对板梁结构在特定频带内响应的研究提出了板和梁结构的波长准则，对于梁结构，一般要求单个梁的长度至少大于5 倍的弯曲波长；对于板结构，板的特征长度要求大于2.4 倍的弯曲波长。

Moens[34]通过对不同形状的板的研究指出，如果板结构的特征长度小于2.4，动能和势能的相等性就无法得到保证。

此外，Langley[35]指出，在强阻尼情况下，直接场在结构响应中占比很大，在板结构中，由EFEA能量密度方程描述的能量密度分布是成正比，而实际的能量密度分布应该是成正比，其中r柱坐标中响应点与激励点之间的距离。因此，在直接场占比较大的情况下，如关注频率较高时或者阻尼比较大时，相对于实际值EFEA 的结果一般表现为，在激励点附近较小而在离激励点很远的地方则相对较大。

Xiang jie[36]通过辐射能量传输方程给出了验证板结构EFEA 结果有效性的准则（公式(19)），文中指出EFEA 基于混响场假设，而公式(19)可以用来判断结构是否满足混响场假设。对于阻尼越大，频率越高，板的特征尺寸越大，直接场部分耗散的能量会更多，而进入混响场的能量就会相对变小，从而导致不满足文中提出的混响场假设

3 非平面波假设的改进

第2 节的推导方法是EFEA 常用方法，该方法实际需要假设结构内的波满足平面波假设[7,8]。根据文献[4]和[36]，在点激励作用下，如果直接扩散场占主导，则平面波假设是不满足的，而混响场占主导时，由于各个方向的波是均匀分布的，可以满足平面波假设。因此，可以考虑将板的响应分为直接扩散场和混响场两个部分[37,38]，即

其中，下标“total”表示总能量，“dir”代表直接场的能量，“rev”代表混响场的能量。

直接扩散场的能量密度可以用公式(21)来表述[8]，而混响场部分的能量可以通过公式(8)来描述。

其中，r为距离激励点的距离。

以一个四边简支单板为例，板的尺寸为1.5m×1.5m，厚度为0.002 m，材料参数如下：密度2700kg/m3，杨氏模量71×109N/m2，泊松比为0.33。在中心点位置施加一个频带400-500 Hz 区间的随机点激励，力的幅值大小为10 N。在400-500 Hz 区间内，板共有33 阶模态，有限元能量结果在频带内取平均值，然后将结果在一个波长上取平均值。

对于单板系统，直接场能量在到达结构边界的时候会发生反射，而反射的功率流则作为混响场的能量输入，即在结构的边界，能量流满足公式(22)

板在x=0.75 m 中线上的响应如图4 所示。图注中的“averaged”表示有限元平均后的结果，“rev”表示EFEA 计算的混响场能量，“dir”表示公式(21)计算的直接场能量，实心○标注的是基于面波公式的结果。图4 结果所采用的滞后阻尼系数为0.01，根据公式(19)计算得到判定系数为0.32，值略小于1。可以发现，此时直接场的能量相对于混响场的能量小了很多，与有限元结果相比，EFEA 基于面波的公式计算结果在激励点位置偏小，在边界位置偏大，这与上节的预期相符[8,35]。同时由于在基于面波的公式推导中忽略了近场项，这也导致了EFEA 结果在激励点和边界位置出现一定的偏差。此外，有限大板在中线和对角线位置的响应要比其他位置大，所以用中线位置的结果进行对比看起来差别较大，实际上差别较大的位置主要集中在激励点附近以及中线和对角线位置，其他位置差别并不是很大，各种方法得到板的整体能量是基本相同的。整体结果对比可以得到，EFEA 基于面波的结果与SEA计算的能量密度平均值基本差别不大，而考虑了直接场能量的结果与有限元结果整体吻合较好。

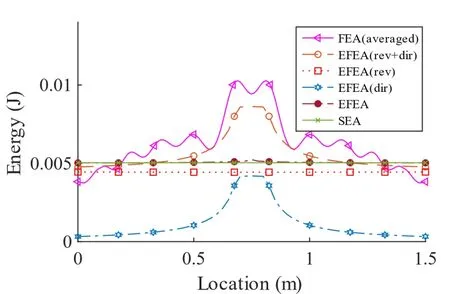
图4 板在x=0.5 m 中线位置的响应（滞后阻尼系数为0.01）Fig.4 Response of the plate at x=0.5 m with damp loss factor is 0.01

将阻尼系数设置为0.1，此时由公式(19)计算的判定系数为3.19，值略大于1，结果如图5 所示。可以发现，此时混响场的能量相对直接场的能量整体小了很多，两者叠加后的总能量与有限元结果差别较小，基于面波的公式此时仍然表现为在激励点处值偏小而在边界位置值偏大，但与SEA 给出的平均值比较，EFEA 给出的能量密度分布相对更接近有限元的结果。

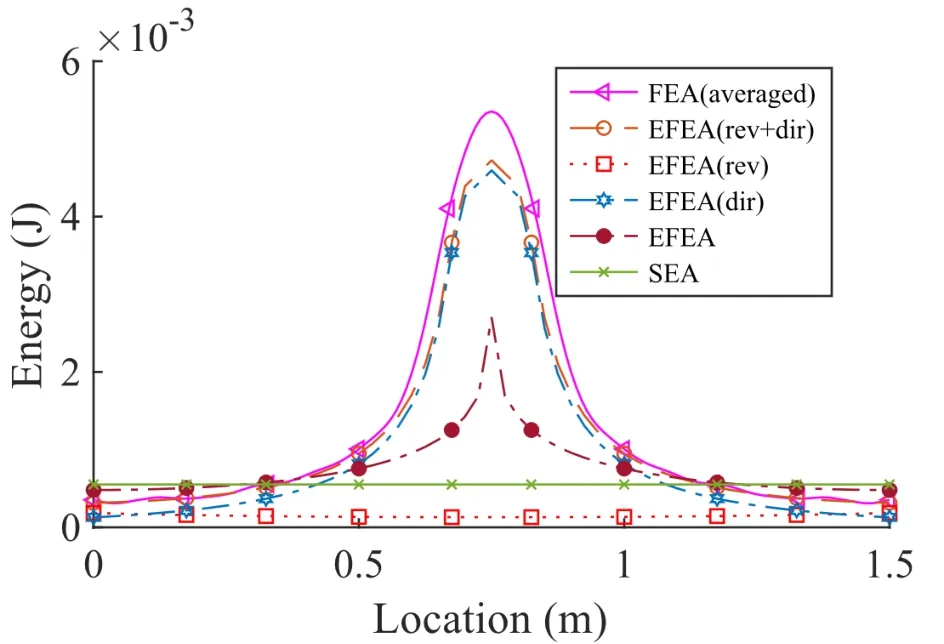
图5 滞后阻尼系数为0.1 时，板在x=0.5 m 中线位置的响应Fig.5 Response of the plate at x=0.5 m with damp loss factor 0.1

通过两组结果的比较可以发现，采用直接场叠加混响场能量的结果整体与有限元的结果更为吻合，同时也可以发现，滞后阻尼系数为0.01时，误差相对更大一些，这是由于在EFEA 公式的推导中，一般会忽略近场项，当阻尼系数较大时，近场项很快就衰减到很小值，而阻尼系数较小时，近场项的影响就更加明显。公式(21)给出的结果实际上仅当k·r远大于1 时是有效的[39]，公式在r=0的位置是奇异的，因此在k·r接近于1 的值附近，可以使用r=0 附近的平均值来代替，在本例中，r=0 附近的值用k·r=2 的平均值来代替。

类似的，对图6 所示的四边简支耦合板进行能量有限元分析，两个板的尺寸均为1.5m×1.5m，厚度分别为2mm 和4mm，材料参数如下：密度2700kg/m3，杨氏模量71×109N/m2，泊松比为0.33。在其中一个板的中心位置(图6 所示)施加一个作用于400-500Hz 区间内随机点激励，通过有限元分析可得耦合模型在400-500Hz 区间内共有49阶模态。

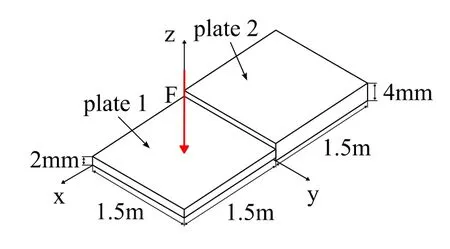
图6 四边简支耦合板Fig.6 Coupling plates with simply supported on all edges

耦合板在内部边界以及耦合边界满足以下能量流平衡条件，

假设直接场传入其他板的能量满足平面波假设，则当滞后阻尼系数为0.01 时，耦合板的在x=0.5 m 位置的响应如图7 所示。公式(19)计算的判定系数和单板相同，此时直接场能量除了在激励点位置附近外，其他位置的能量相对小很多，所以基于面波的公式在距离激励点较远的位置（例如靠近边界以及其他板）误差相对较小。

图7 滞后阻尼系数为0.01 时，耦合板在x=0.5 m 中线位置的响应Fig.7 Response of the plate at x=0.5 m with damp loss factor 0.01

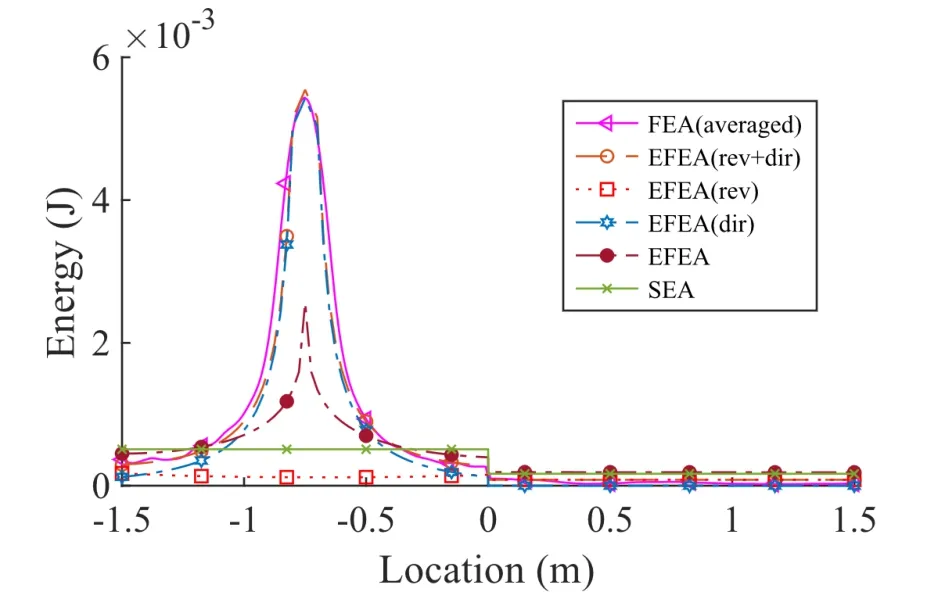
图8 滞后阻尼系数为0.1 时，耦合板在x=0.5 m 中线位置的响应Fig.8 Response of the plate at x=0.5 m with damp loss factor 0.1

滞后阻尼系数为0.1 时，直接场的能量占主导，此时在远离激励点位置的能量以及混响场的能量几乎可以忽略。基于平面波的公式在这种情况下的结果相对SEA 具有一定的优势。对于耦合板，不同阻尼的情况下，通过单独计算直接场能量和混响场能量的方法结果与有限元结果更加接近，这与四边耦合单板的结果时一致的。

4 结论

本文简述了能量有限元研究进展，并通过平面波假设，说明了以波动解为基础的物理模型都可以使用能量有限元的推导方法得到能量平衡关系。对于目前在EFEA 中使用的一些可靠性评估方法进行了系统的解释。对于非平面波的情况，如点载荷作用下的板，以四边简支单板和耦合板为例，对板在直接场和混响场占主两种导情况下（分别对应两种阻尼大小）的响应结果进行对比分析，计算结果与具有足够网格密度的有限元结果进行了比较，结果表明，对于单点载荷作用下的平板结构，直接场的能量对激励点附近的响应结果影响很大，而阻尼足够大时，结构中的能量以直接场的能量占主导，传统平面波假设的公式对能量密度的估计会出现较大的误差，当阻尼很小时，能量密度分布趋向于平均，但近场项等其它因素对结果的影响会更加明显。仿真结果也表明，对于点载荷作用的情况，通过分别计算直接场和混响场能量的方法可以改善EFEA 的计算结果。