升力式面对称运载器大攻角颤振分析方法研究

蔡巧言 吕计男 郭力 王昕江

(1 中国运载火箭技术研究院,北京 100076；2 北京宇航系统工程研究所,北京 100076；3 中国航天空气动力技术研究院,北京 100074）

0 引言

颤振作为复杂的气动弹性现象，一旦发生往往在几个周期内就会使飞行器结构发生破坏。国家军用标准与民航适航条例中对飞行器颤振分析均有明确的要求。

升力式布局面对称运载器外形复杂，往往由异型截面机身、大翼展机翼、多组气动舵面组成，飞行剖面具有大空域、宽速域的特点，因此运载器面临的气动力环境非常复杂。特别是运载器返回减速需求使得此类飞行器返回飞行段多采用大攻角飞行形式，当运载器大攻角飞行时运载器机身对舵面产生较大干扰，使得舵面前方来流不再表现为自由来流流动结构，特别是运载器后部的V 尾几乎完全处于前体尾流干扰区内，进一步增加了其绕流流场的复杂性。同时，运载器结构广泛使用先进复合材料，V 尾弹性频率低，模态振型复杂。在复杂的流动环境与结构动力学特性共同作用下，V 尾结构易与气动力耦合发生颤振，因此需要在方案设计初期即对其颤振特性进行准确分析，减小飞行风险。传统颤振工程计算方法对小攻角条件下气动控制面的亚声速/超声速颤振分析结果可满足工程初步设计阶段的精度要求。对于跨声速域及复杂扰流环境，工程气动力模型难以实现非定常气动力的准确描述。杨超[1]对高超声速气动弹性力学研究中的不同工程气动力模型及CFD/CSD 时域计算方法进行了综述，给出了不同方法的适用范围与计算优劣。杨炳渊等[2]针对翼面大攻角颤振给出了一种当地活塞理论计算方法，使用算例证明了该方法在有限厚度翼面大攻角颤振中的可行性。金伟[3]对先进战斗机全动 V 尾抖振强度进行了研究，使用RANS/LES 混合方法对大迎角飞行状态下的V 尾扰流流场进行计算，并使用CFD/CSD 方法对其抖振特性进行了分析。对于升力式布局面对称运载器超声速大攻角返回飞行而言，受大攻角飞行下大范围分离非定常流场复杂流动特性影响，传统工程气动力方法难以实现流场准确计算。设计中需要采用基于计算流体力学/计算结构动力学（CFD/CSD）耦合求解的数值方法，在精确模拟流场的基础上研究运载器颤振特性。

本文分别采用基于CFD 和工程气动力模型的颤振分析方法，对升力式运载器大攻角飞行状态下V 尾的颤振特性进行计算，对两种方法计算结果进行对比，分析了工程气动力方法在此类飞行器大攻角颤振分析中的不足，提出类似问题需要在工程研制中引起关注。

1 颤振分析方法

常用的颤振仿真分析方法有工程气动力[4,5]方法和CFD/CSD 方法[6-12]。

1.1 工程气动力方法

时域颤振计算的控制方程可以表示为式（1）所示

式中，M为质量矩阵，D为阻尼矩阵，K为刚度矩阵，u为结构节点位移向量，Ma∞为来流马赫数，k为减缩频率，Fa为作用在结构上的气动力。

根据工程气动力模型，每个面元上的压力值与面元下洗的关系可以表示成影响系数的形式，此时Fa可以表示为

式中，Ma∞为来流马赫数，k为减缩频率，ρ∞为来流密度，U∞为来流速度。A为气动力影响系数矩阵，是减缩频率与来流马赫数的函数。w为面元下洗向量。实际分析中，一般通过模态坐标投影，对模态坐标下的气动弹性控制方程进行求解

式中，M,D,K分别为模态质量矩阵、模态阻尼矩阵与模态刚度矩阵。q为广义坐标向量，Q=φTFa为广义气动力向量。φ为模态振型向量组成的振型矩阵。分析中采用基于统一升力面理论（ZONA7U）的工程气动力模型。通过求解式(3)得到飞行器颤振特性。

1.2 CFD/CSD 耦合分析方法

CFD/CSD 耦合分析方法中CFD 计算模型对V 尾颤振特性的准确预测至关重要。对于没有气动干扰的气动控制面，只需考虑控制面运动产生的非定常气动力，采用基于雷诺平均（RANS）模式精确模拟近壁面的流场结构即可满足分析要求。但对于大攻角飞行时处在飞行器前体干扰下的V 尾，仅模拟壁面附近的流场不能准确反映前机身脱体涡对V 尾的影响，需采用更精确的流场模拟数值方法[3,7]。大涡模拟方法（LES）方法能精确求解大范围的气流分离和不稳定流动，但由于计算效率低下的问题，不适用于实际工程问题分析。本文采用RANS/LES 的DES（Detached Eddy Simulation）混合算法，分析V 尾的颤振模式。DES 方法在气动控制面壁面区域具有RANS方法的性能，在流动分离区表现为LES 方程的性能[3,10,12]。V 尾颤振具有模态频率低、多模态耦合和响应位移大的特点。本文在CFD/CSD 耦合求解方法引入预估矫正迭代方法进一步提高分析精度，采用基于RBF 方法的网格变形技术保证求解鲁棒性[8]。CFD/CSD 计算流程示意图如图1 所示。

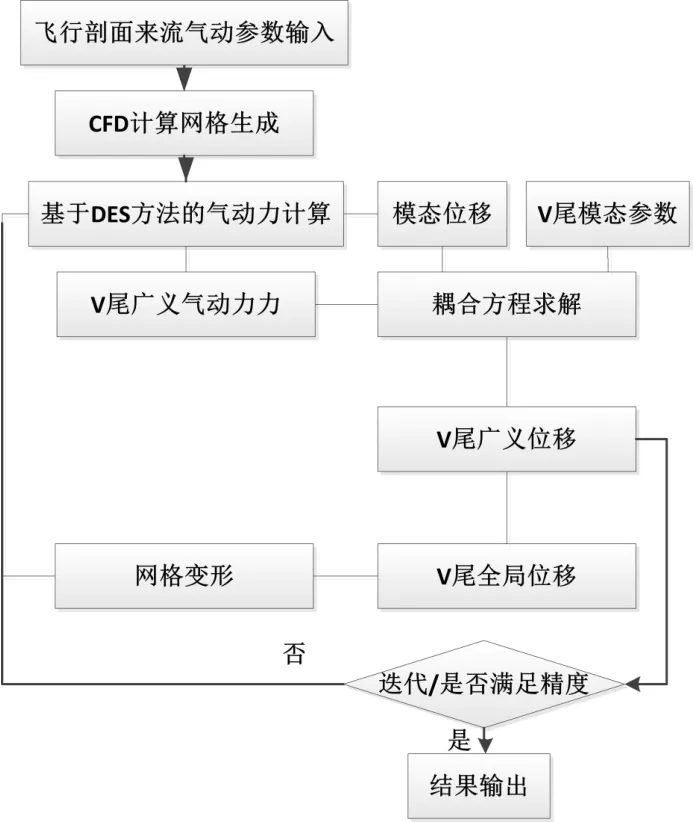
图1 CFD/CSD 计算流程示意图Fig.1 CFD/CSD calculation process diagram

2 结构动力学模型

V 尾颤振计算需要考虑所有和V 尾相关的弹性模态。使用Patran 软件的Cquad4 和Cquad8 壳单元模拟蒙皮，使用壳单元与Cbar 梁单元模拟主要承力结构，使用Conm2 集中质量单元模拟主要质量部件，建立V 尾有限元动力学模型，如图2所示，设置自由-自由边界条件。

图2 V 尾有限元模型Fig.2 FEM model of V-tail

采用Lanczos 方法对有限元动力学模型进行动力学分析，获得所有和V 尾相关的弹性模态频率和振型，其中前4 阶为V 尾组合模态，第5 阶为V 尾扭转模态。CFD 颤振计算所用三维振型如表1 第3 行所示。使用薄板样条TPS 方法（Tin Plate Spline Method）将所有和V 尾相关的弹性模态振型向面元网格插值，工程气动力方法颤振计算所用振型如表1 第4 行所示。

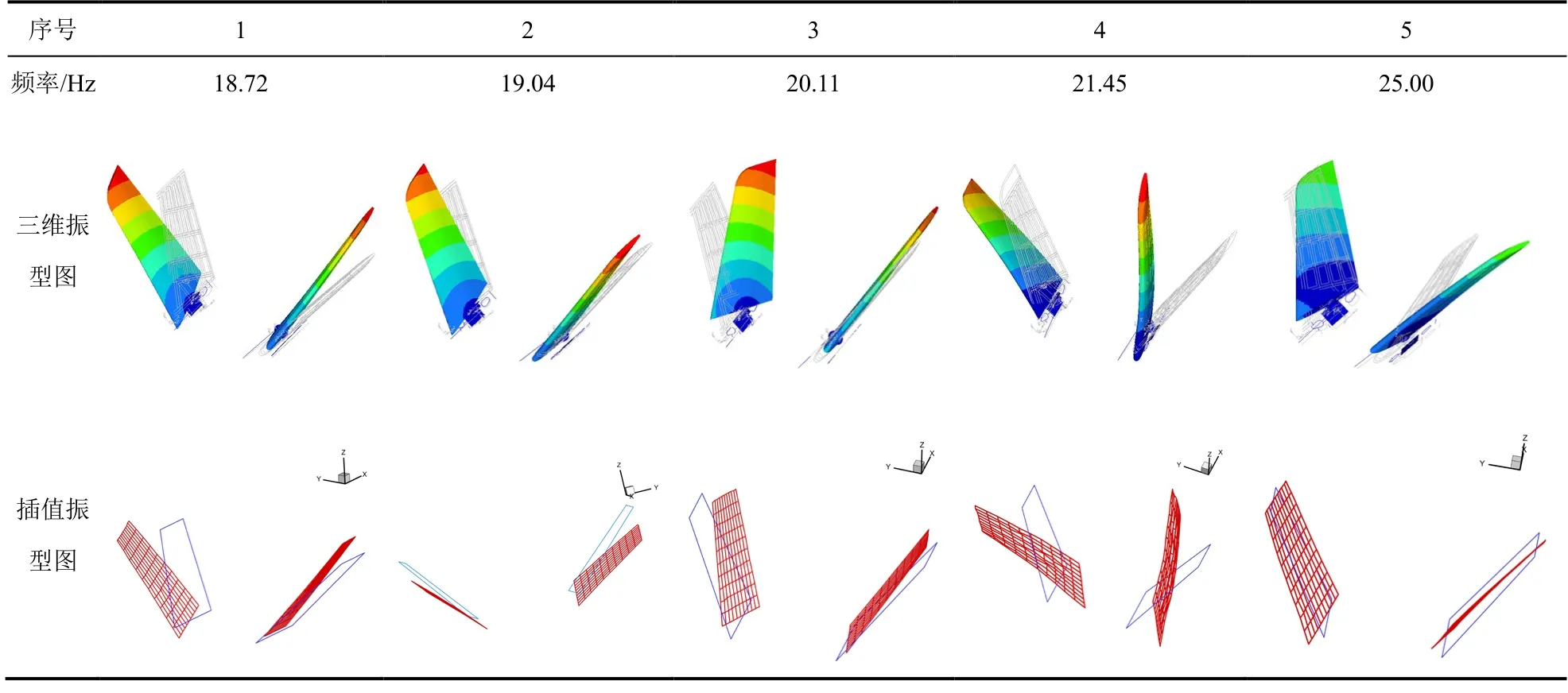
表1 V 尾弹性模态振型Table 1 Modal shapes of V-tail

3 颤振分析

选取大攻角返回特征飞行状态，马赫数2.3攻角18°。分别采用工程气动力/CSD 方法和CFD/CSD 方法开展颤振分析。

3.1 基于工程方法的颤振分析

采用ZONA7U 方法建立超声速非定常气动力模型，采用表1 中V 尾弹性模态，在频域进行颤振分析。分析得到各阶模态“动压-阻尼”曲线与“动压-频率”曲线如图3 所示。

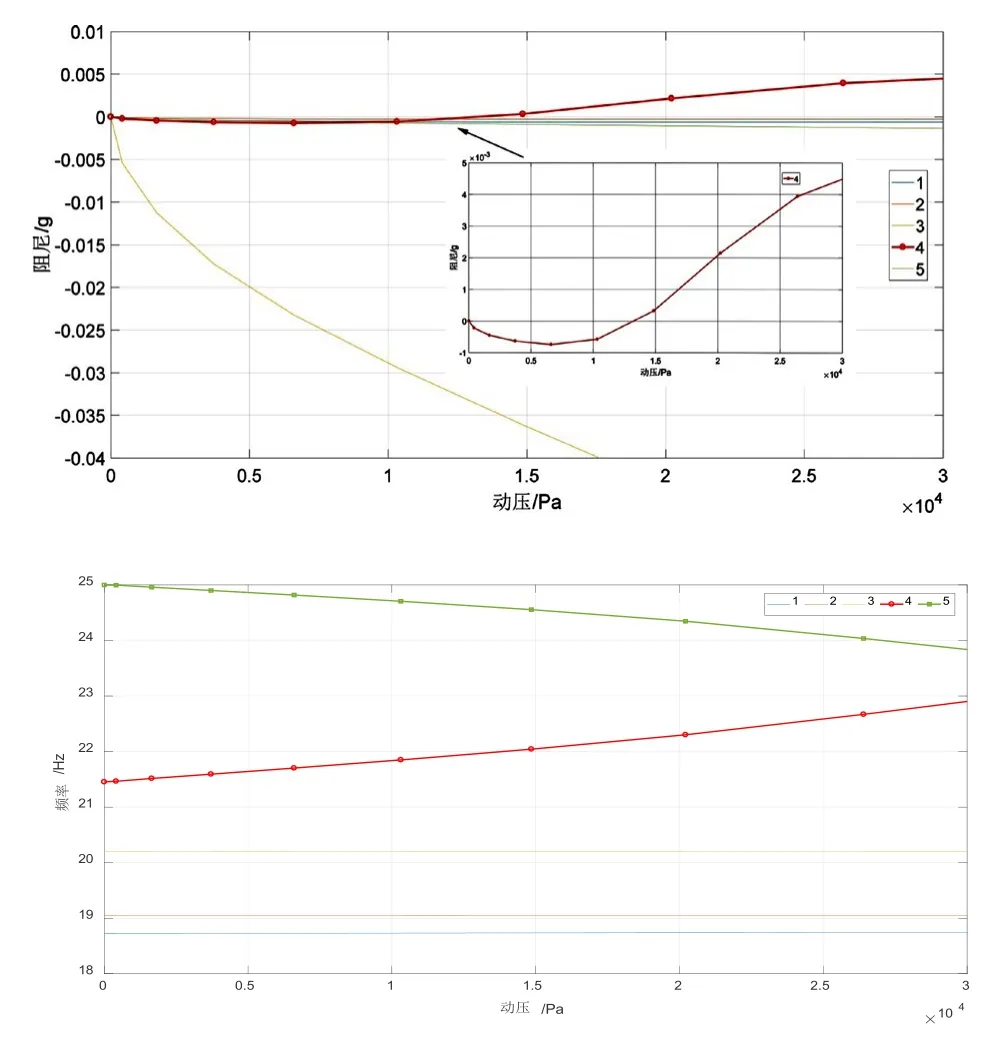
图3 各阶模态“动压-阻尼/频率”曲线Fig.3 Dynamic pressure-damping/frequency curve

分析“动压-阻尼”曲线与“动压-频率”曲线可见，工程方法计算得到的颤振动压为11.3kPa。其中，第4 阶模态动压-阻尼曲线过零。通过模态剔除分析，确定第4 阶、第5 阶V 尾模态为颤振的主要参与模态。

3.2 基于CFD 方法的颤振分析

相同来流状态马赫数2.3、攻角18°，采用CFD 与V 尾弹性模态耦合的分析方法开展V 尾颤振分析。CFD 计算采用DES 模型，结构模态阻尼取0，采用变动压分析方法开展CFD/CSD 计算。通过各阶广义模态位移的时域响应，判断颤振动压与发散模态。来流动压11.3kPa 时，CFD/CSD 计算结果显示（图4）V 尾第4 阶、第5 阶弹性模态均未发生颤振发散。不断提高来流动压进行颤振计算，直到来流动压达到22.2kPa 时，V尾第4 阶、第5 阶弹性模态的广义坐标才出现小幅近似等幅振动。来流动压22.2kPa 时，V 尾5阶广义模态位移时域响应曲线如图5 所示。其中，第1～3 阶广义模态位移时域响应均为收敛状态，第4 阶模态呈现缓慢发散趋势，第5 阶模态呈现极限环等幅震荡趋势。

图4 广义模态位移时域响应（11.3kPa）Fig.4 Generalized displacements in time domain(11.3kPa)

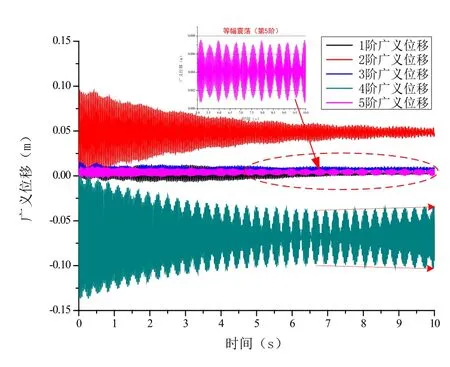
图5 广义模态位移时域响应（22.2kPa）Fig.5 Generalized displacements in time domain (22.2kPa)

不同动压第4 阶广义位移对比如图6 所示，可见，11.3kPa 来流动压时，第4 阶广义位移呈现周期性缓慢衰减状态，阻尼比约0.2%；22.2kPa来流动压时第4 阶广义位移呈线性小幅增长状态，阻尼比约-0.4%。在颤振点附近，阻尼呈现非线性特征。

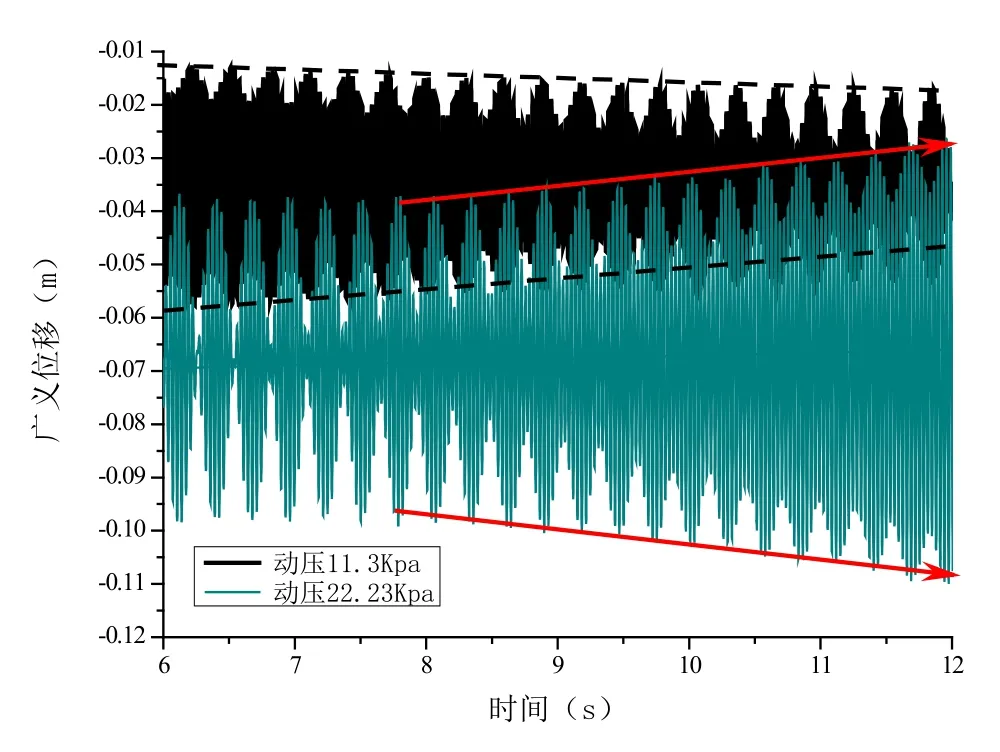
图6 不同动压下V 尾广义位移Fig.6 Generalized displacements in time domain of V-tail

3.3 颤振特性差异分析

工程气动力方法与CFD 方法预示颤振动压分别为11.3kPa 和22.2kPa，两者相差将近一倍，V 尾颤振特性差别较大。对流场进行精确分析，V 尾三个不同站位（Y=0.68/1.29/1.69m）截面流场当地动压如图7 所示，其中，Y为飞行器全局坐标系法向。自由来流经运载器头部脱体激波后，流场压力上升，速度下降。经过机身产生的膨胀波后流动加速，压力下降。V 尾附近流动压缩产生激波，使得V尾附近流场处于局部亚声速状态。由于大攻角逆压梯度存在、激波附面层干扰，在V 尾前部产生大范围分离，进而影响V 尾附近流场分布，流动结构非常复杂。在左侧 V 尾Y=0.68/1.29/1.69m（图7）的展向站位上，分别取靠近前缘上表面、后缘上表面、前缘下表面与后缘下表面处的4 个特征点，对特征点处的来流动压进行测量。随着展向站位Y 值增加，前缘上表面特征点处的当地动压分别为1.13kPa、17.75kPa与19.32kPa；后缘上表面特征点处的当地动压分别为6.61kPa、8.86kPa 与7.29kPa；前缘下表面特征点处的当地动压分别为22.67kPa、18.12kPa 与20.50kPa；后缘下表面当地动压分别为12.95kPa、14.09kPa 与16.88kPa。三个站位截面当地动压与自由来流动压22.2kPa 存在较大差异；此外，随着展向站位变化，各特征点处当地动压值的大小也发生变化。

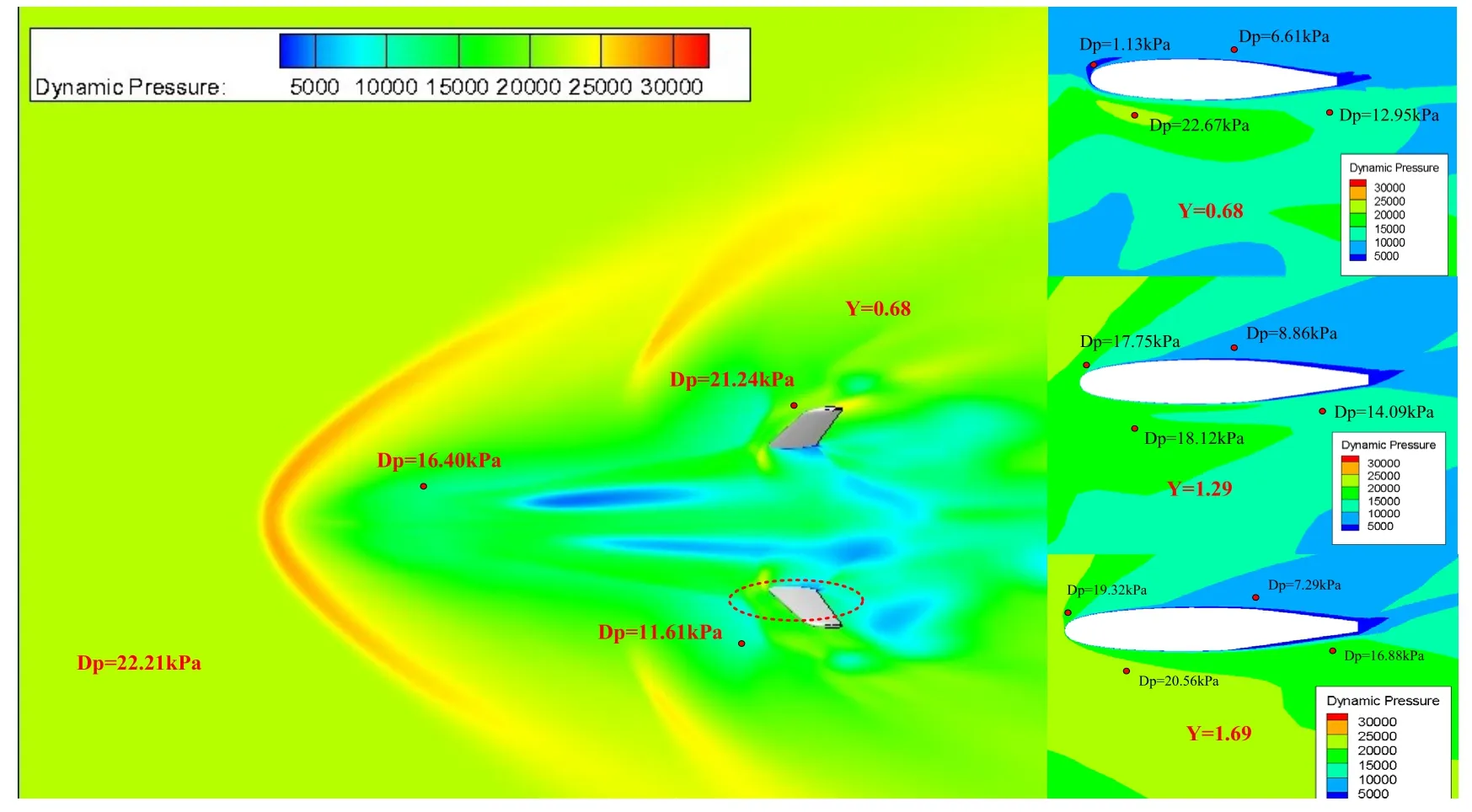
图7 V 尾典型截面流场云图Fig.7 Dynamic pressure contour of typical section

对比工程气动力方法与CFD 方法得到的压力系数（图8）。根据CFD 计算结果，左侧V 尾背风面的压力系数与其迎风面相比可以近似视为均匀分布。此时，截取左侧V 尾不同展向站位截面，并提取截面前缘、中部与后缘特征点处的表面压力系数，与背风面对应位置压力系数相减，可以得到不同特征点处CFD 计算得到的表面压差系数。从根部特征截面到梢部特征截面，CFD计算左侧V尾前缘特征点处的表面压差系数分别为0.96、0.14 和0.03；中部特征点处的表面压差系数分别为0.61、0.23 和0.07；后缘特征点处的表面压差系数分别为0.51、0.28 和0.11。

不同特征点处CFD 计算的压力系数显示，左侧V尾前缘高压力系数区域随着展向站位的增加不断向后缘扩展，这与工程气动力方法计算得到的表面压差系数分布规律存在较大差异。

图8 为两种方法得到的V 尾表面压力云图。经分析，在计算状态下，运载器头部激波、机身压缩作用，在V 尾前方已出现激波（自身产生激波），使其表面局部出现亚声速区，并出现分离区，工程气动力方法已不能反映该流动结构。CFD方法比较准确的预示了当地的流场结构，对展向和弦向流动引起的压力变化预示准确，较好的描述了前缘高压区和尾缘及翼尖的低压区的位置。

不同马赫数、飞行攻角前体对V 尾的干扰特性不同，V 尾的当地动压/压力分布变化规律也不同。采用固定马赫数（Ma2.3）和固定来流动压（22.2kPa）变换攻角（8°/18°/28°）的方式研究攻角的影响（图9）。整体规律上看，在所计算攻角范围内，V 尾都会发生小阻尼发散。不同的是，随着攻角增大，V 尾更早进入等幅震荡状态，这主要是不同迎角下，前体对V 尾的干扰不同，V尾局部亚声速区域范围不同导致。

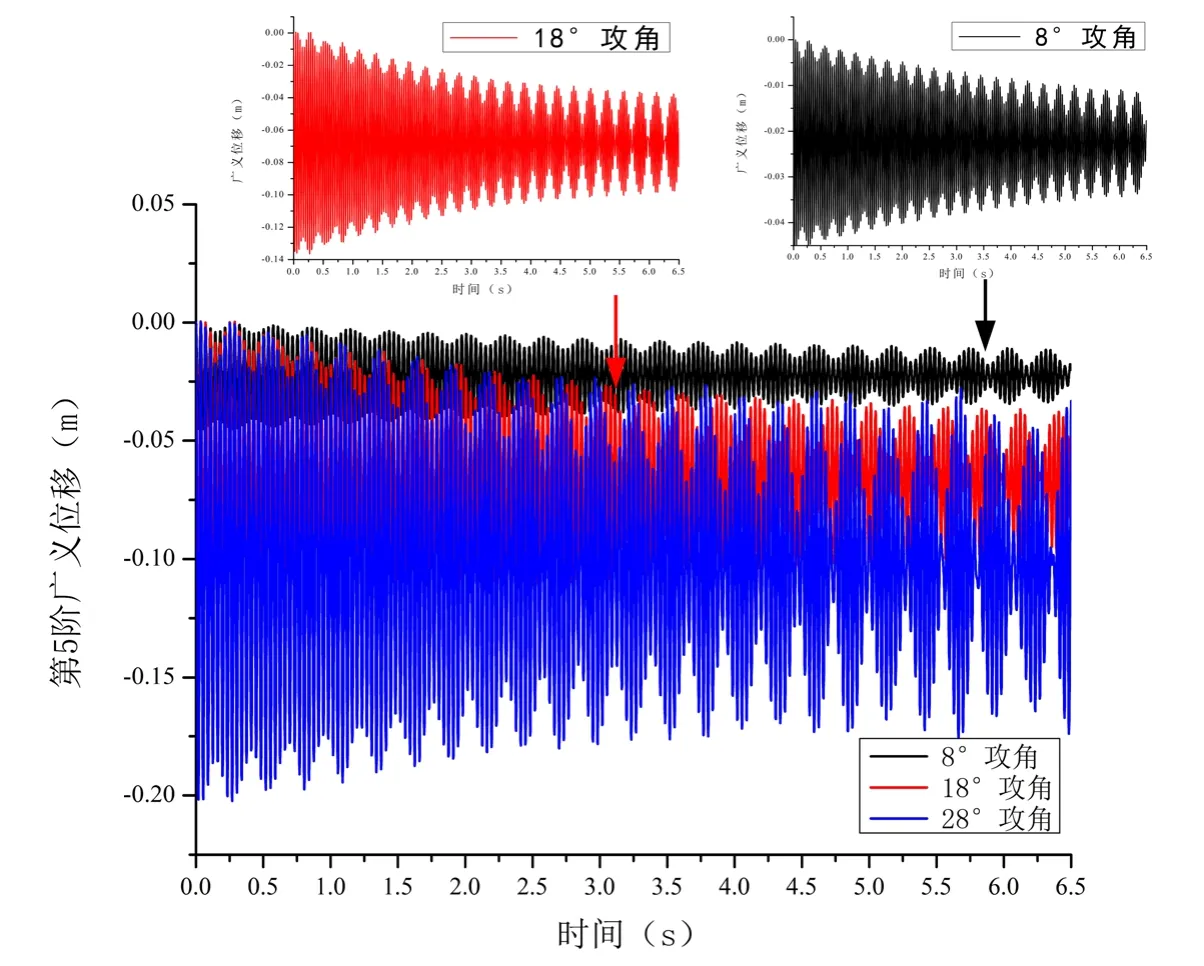
图9 攻角对颤振的影响Fig.9 Influence of angle of attack

总之，通过对流场进行精确分析，发现工程气动力方法与CFD 方法预示颤振动压产生较大偏差的直接原因是两种分析方法得到的压力分布和当地动压不一致导致，工程方法没有反映出机身波系及大攻角分离对舵面前方来流流场的干扰影响。

4 结论

本文通过分析升力式布局面对称飞行器V尾大攻角飞行状态下的颤振特性，发现工程气动力频域方法和CFD/CSD 时域方法在预示中存在较大差异，工程气动力方法分析结果过于保守，易使总体设计发生误判，采取额外的刚度补偿，增加结构设计代价。通过对升力式布局面对称运载器大攻角扰流流场开展分析，认为当地动压和压力分布的差异是导致工程气动力和CFD 方法存在差异的主要原因。工程设计中需要辨识飞行剖面内气动干扰严重的区域，在此区域需采用基于CFD 的数值方法开展精细的流动特性分析才能对颤振特性开展准确的预示与评估。