质量砝码和压力砝码活塞式压力计的计量误差
庞桂兵, 杨 逸, 樊双蛟, 杨远超
(1.大连工业大学 机械工程与自动化学院,辽宁 大连 116034;2.中国计量科学研究院,北京 100029)
1 引 言
活塞式压力计是依据流体静力学原理和帕斯卡定律,以流体作为压力传递介质,利用活塞及承重部件和专用砝码加载在活塞有效面积上的重力与作用在活塞下端面的被测压力相平衡的原理而制成的压力计量仪器[1~5]。活塞式压力计的计量误差多来自于活塞系统,活塞有效面积是影响计量误差的主要因素之一,尤其是在高压计量时,活塞有效面积会产生较大变化,从而影响计量结果[6~8]。
我国目前的活塞式压力计主要使用压力标称砝码(以下简称压力砝码),每一块砝码均标有整数压力值。现行活塞式压力计检定规程中规定:测量上限25 MPa及以上的活塞式压力计的专用砝码若以标称压力的形式配备,需要对每一块砝码质量进行补偿修正,并进行编号以规定其在使用中的加载顺序[11,12]。压力砝码中,无编号的小砝码压力值均根据活塞零压有效面积计算,在实际测量时,测量压力值的升高通常伴随着活塞有效面积的增大,因此在全量程范围内,重复使用无编号的小砝码会产生不可避免的误差。国外活塞式压力计主要使用质量标称砝码(以下简称质量砝码),配置计算和显示终端,根据砝码质量组合值和该值对应的活塞有效面积,实时计算实际压力值。根据这2种砝码的计量原理可知,质量砝码能够避免压力砝码只能按照固定活塞面积预先调整质量带来的问题,有利于提高活塞式压力计的计量准确度。
目前在此方面的研究主要集中于形变系数和活塞结构,Wladimir Sabuga[13]等使用有限元法和实验法研究了1 GPa压力条件下的形变系数和不确定度;Hiroaki Kajikawa[14]等研究了基于Heydemann-Welch模型的可控间隙活塞缸的压力形变系数;Fitzgerald M P[15]等通过实验和理论方法研究了活塞的压力平衡与弹性变形;Yang Y C[16]等通过扩展测量方法测定了500 MPa压力条件下自由形变活塞的形变系数。形变系数和活塞结构方面的研究[17]为提高活塞式压力计的计量精度奠定了理论基础,但关于砝码类型对计量精度影响方面的研究尚未发现公开报道。鉴于我国压力计量对标国际先进水平的迫切要求,对压力砝码和质量砝码的计量精度进行系统性研究十分必要。
本文针对自由形变活塞,以形变系数对活塞有效面积的影响为基础,推导了输出压力计算公式;进而建立使用压力砝码和质量砝码时,输出压力的相对误差模型;以10~510 MPa量程的活塞式压力计为研究对象进行误差实例对比分析,为从计量原理上减小误差,实现高精度活塞式压力计的研制提供依据。
2 输出压力计算
2.1 输出压力与活塞有效面积
根据活塞式压力计的计量原理,在重力加速度确定条件下,输出压力与砝码质量和活塞有效面积有关:
(1)
式中:m为砝码质量,kg;g为重力加速度,m/s2;A为活塞有效面积,cm2;p为输出压力,MPa。
活塞有效面积会随着被测压力值改变,引入活塞形变系数λ进行修正[18],则式(1)可表示为:
(2)
式中:λ为活塞形变系数;A0为活塞零压有效面积,cm2。
使用压力砝码时,砝码上标称的是压力值,砝码质量需要按照所标称的压力值预先计算,即计算砝码质量时需要预先考虑形变系数对活塞有效面积的影响,由于是预先考虑该影响,因此活塞有效面积只能按照某一压力点的形变系数来计算。现行规程规定按照大砝码质量的组合即压力间隔点所对应的压力值来计算有效面积,压力间隔点对应的活塞有效面积可表示为:
Ai=A0(1+λnp0)
(3)
式中:p0为单块大砝码产生的压力值,MPa;n为砝码数量;Ai为压力间隔点所对应的活塞有效面积,cm2。
使用质量砝码时,输出压力值根据实际加载的砝码质量计算获得,按照所加载砝码对应的实际压力值计算出的活塞有效面积:
Am=A0(1+λpact)
(4)
式中:pact为加载质量砝码对应的实际压力值,MPa;Am为实际压力值对应的活塞有效面积,cm2。
由式(3)和式(4)可知,如采用压力砝码或质量砝码获得压力值,计算输出压力时,所使用的活塞有效面积不同,因此计算结果也不同。
2.2 使用压力砝码的输出压力计算
压力计砝码一般由1组大砝码和1组小砝码组成,大砝码质量为m1=m2=…=mi,小砝码质量为m0i(其中i为大于0的任意正整数),满足m01+m02+…+m0i=m1,即大砝码压力间隔范围内的压力值可以通过配置小砝码实现。
根据2.1节的讨论,在配置压力砝码的质量时,计算大砝码质量需要考虑形变系数对活塞有效面积的影响,计算小砝码质量则采用相同形变系数获得的活塞零压有效面积计算,该计算方式会对输出压力产生影响,且在不同压力段内影响的程度不同。
1) 压力范围为0~p0
产生0~p0范围内的压力时,加载部分或全部小砝码,输出压力计算值为:
(5)
式中:p0i为单块小砝码产生的压力值,MPa;m0i为单块小砝码的质量,kg。
2) 压力范围为np0~(n+1)p0
产生np0~(n+1)p0范围内的压力时,加载大砝码和小砝码,通过质量组合计算输出压力为:
p=np0+∑p0i
(6)
式中:mi为单块大砝码的质量,kg;p0为单块大砝码产生的压力值。
因此,计算大小砝码质量时使用的零压有效面积不同,必然会产生输出压力误差。
2.3 使用质量砝码的输出压力计算
使用质量砝码时,预先计算加载的砝码质量,再计算对应该质量的活塞有效面积,然后计算实际压力值。当砝码产生np0~(n+1)p0范围的压力时,需要加载大砝码和小砝码,通过其质量组合获得输出压力为:
(7)
3 输出压力误差模型
3.1 输出压力误差公式推导
根据式(6)和式(7),可以计算不同压力范围内,输出压力的相对误差。
1) 压力范围为0~p0
当砝码产生0~p0范围的压力时,使用质量砝码与使用压力砝码获得压力的相对误差为:
(8)
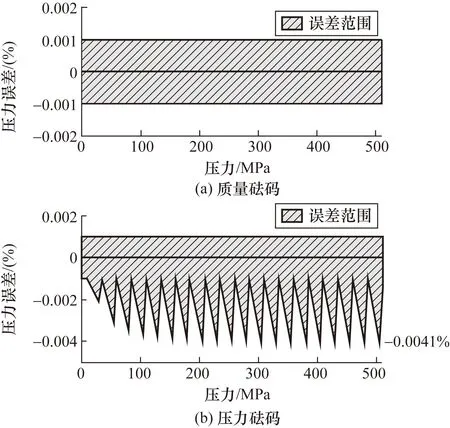
由于pact Δprel=λpact<λp0 (9) 2) 压力范围为np0~(n+1)p0 当砝码产生np0~(n+1)p0范围的压力时,由式(6)和式(7)可知pact Δp=p-pact (10) 当pact取当前压力范围内的最大压力值时,即将pact=(n+1)p0代入式(10)得到绝对误差最大值: (11) 根据式(5)和式(6),化简式(11)得: (12) 根据第2.2节的讨论,所有小砝码质量之和等于单块大砝码质量,因此由式(12)可推导出绝对误差最大值的通项公式为: Δpmax=p0λnp0+∑p0iλ(n+1)p0 (13) 将pact=(n+1)p0代入式(13),得绝对误差的通项公式为: Δp=np0λ(pact-np0)+∑p0iλpact =(np0+∑p0i)λpact-λ(np0)2 (14) 因此,得相对误差和最大相对误差的通项公式分别为: (15) (16) 由式(15)和式(16),可知: (17) 根据式(15)和式(16)可计算np0~(n+1)p0内任意压力值的误差范围,当n=0时,为0~p0的压力误差范围,即式(8)。 以量程为10~510 MPa、准确度等级为0.005级的自由形变活塞式压力计为例讨论。活塞组件材料为碳化钨,一般采用的[16]活塞截面积为0.02 cm2,压力形变系数为8.46×10-7MPa-1。采用压力砝码时,砝码公称质量、对应压力值及砝码数量如表1所示,使用21个砝码可形成510 MPa范围内间隔 5 MPa的任意压力值。 表1 510 MPa活塞式压力计的砝码质量 根据式(16),可计算10~510 MPa全量程范围内的压力误差,结果如图1所示。根据GB/T 30432-2013[19],0.005级压力计的砝码质量相对误差允许值为±0.001%,即使用质量砝码时,输出压力误差的可能范围为±0.001%,如图1(a)所示。 图1 输出压力相对误差(0.005级压力计) 使用压力砝码时,在不使用小砝码的压力点,压力砝码误差范围下限与同等条件下使用质量砝码相同,为-0.001%,在每个压力段内,随着压力增长,重复使用小砝码产生的误差增大,每个压力段内的最高压力点误差最大。当压力增加到505 MPa时,使用压力砝码产生的压力误差下限达到最大值,为-0.004 1%,比使用质量砝码大0.003 1%,如图1(b)所示。 结果表明,相较于使用压力砝码,质量砝码有更小且更稳定的压力误差范围,同时其压力误差也不会受压力变化影响。 1) 活塞形变系数相同情况下,使用不同类型的砝码,计量精度不同。使用压力标称砝码时,小砝码的压力值均根据活塞零压有效面积计算,在不同的压力组合条件下,重复使用小砝码必然会产生计量误差。使用质量标称砝码时,通过实际加载的砝码质量计算活塞有效面积,进而实时计算输出压力,避免了压力砝码存在的问题。 2) 针对自由形变活塞,以形变系数对活塞有效面积的影响为基础,推导了输出压力计算公式,建立了使用压力砝码和质量砝码时,输出压力的相对误差模型。以10~510 MPa量程的自由形变活塞式压力计为例进行计算,在不使用小砝码的压力点,压力砝码误差范围下限为-0.001%,在每个压力段内,随着压力增长,误差增大,每个压力段内的最高压力点误差最大。当压力增加到505 MPa时,使用压力砝码产生的压力误差下限达到最大值,为-0.004 1%。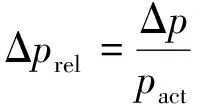

3.2 压力误差对比分析实例

4 结 论

