基于三角形收缩法改进的分数傅里叶变换估计牛顿环参数

武进敏, 姜 盛, 鲁溟峰, 沈德明, 范军芳,李亚峰, 张 峰, 陶 然

(1.北京信息科技大学 自动化学院，北京 100192；2.北京理工大学 信息与电子学院，北京 100081)

1 引 言

由于干涉测量技术具有较高的测量精度和灵活度[1,2],在光学测量领域得到较为广泛的应用[3～8],其测量参数包括测量元件曲率半径、光源波长、介质折射率、物体面形等关键物理量[9～12]。由于干涉测量技术是以干涉条纹图像作为结果输出,因此干涉测量技术中的关键环节是分析处理所采集的干涉条纹图。牛顿环干涉条纹是一种典型的干涉条纹图,目前,有关学者已提出针对牛顿环条纹图分析处理的许多方法[13～19],包括:基于条纹周期的分析方法,如数环法;基于傅里叶变换的分析方法,如定心轮廓法。此外,因为牛顿环条纹图其相位具有二次多项式分布规律,此类条纹图在信号处理领域也被称为线性调频信号(chirp信号),所以作为处理chirp信号的最优方法,基于分数傅里叶变换的分析方法于2013年由Lu M F等[20]提出。对于此类方法,重要环节是搜索匹配旋转角,为了精确检测匹配旋转角,需要减小步长遍历搜索范围内的所有旋转角,导致算法时间过长。为了满足工程实际需求,目前采用非均匀搜索[21]的优化方法在保证精度的前提下可以缩短搜索时间,但其易受局部极大值的影响。

为了进一步解决在较短时间内精确检测到匹配旋转角,本文提出基于三角收缩的优化方法,通过分析牛顿环干涉条纹在分数傅里叶域的幅值最大值与相应旋转角分布规律,基于最小二乘拟合证明这一分布规律在匹配旋转角附近具有局部轴对称的特性,从而通过该分布的对称轴来确定匹配旋转角,因此,该方法无需遍历搜索范围内的旋转角,大大减少了时间消耗。

2 理论分析及原理

2.1 牛顿环分数傅里叶域信号处理原理

牛顿环是一种典型的具有二次相位分布的干涉条纹图,如图1所示。

图1 牛顿环干涉条纹

其强度分布可描述为

I(x,y)=I0+Acos[φ(x,y)]

(1)

式中:I0是条纹图背景强度;A是条纹图调制强度;φ(x,y)表示牛顿环干涉条纹的相位,

φ(x,y)=Kπ[(x-x0)2+(y-y0)2]+π

(2)

式中:K=2/(λR);λ表示入射光波长;R是被测透镜曲率半径;(x0,y0)为牛顿环环心坐标。

对于牛顿环条纹图,其行(或列)也是一维chirp信号,数学表达式可以表示为

I(x)=rect(x/Xm)[I0+f(x)+f*(x)]

(3)

式中:*号表达共轭;rect(x/Xm)表示持续时间;而f(x)可以表达为

f(x)=(A/2)exp[jφ(x)]

=(A/2)exp[j(πKx2+2πfcenx+φy)]

(4)

式中:fcen=-Kx0=-2x0/(λR);φy是行(或列)的固定相位。

一维chirp信号的分数傅里叶变换定义为

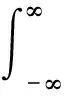
(5)

式中:ux为行信号在分数傅里叶域中的频率;分数傅里叶的核函数,可以描述为

Kα(ux,x)=

(6)

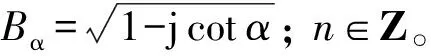
将核函数表达式代入公式(5)可得:

(7)

当旋转角满足

cotα=-K

(8)

牛顿环条纹图每一行(或列)的Fα(ux)表示为

sinc[πXm(uxcscα-fcen)]

(9)

因此,对于一维chirp信号,当旋转角满足式(8)时,其分数傅里叶域幅值分布如图2所示。由图2可知,|Fα(ux)|在fcen=uxcscαm位置处取得最大值,αm相应的即为匹配旋转角。从而根据被测透镜曲率半径与匹配旋转角的关系,R可表示为

(10)

图2 一维信号分数傅里叶域幅值分布

另外,牛顿环环心位置也可由αm下分数傅里叶域幅值最大值的位置计算得到

(11)

2.2 三角收缩优化方法原理

由于在每个旋转角下,牛顿环在分数傅里叶域幅值均有唯一最大值,不同分数域中幅值最大值与相应旋转角α之间的关系如图3所示。图3中最大值对应的α为αm。

图3 分数傅里叶域幅值最大值与相应旋转角关系

由图3可知,幅值最大值分布关于αm具有局部轴对称特性,因此通过确定对称轴,即可得匹配旋转角αm,根据αm可得被测透镜曲率半径。

为了证明幅值最大值分布具有轴对称性,定义新函数FM(α),表示每个旋转角下对应的分数域幅值最大值,数学表达式为

FM(αm)=Max(Fα)

(12)

根据公式(9),公式(11)可以写成

FM(R)=Max(FR)

(13)

现将公式(13)中R改为R-Rm,分数傅里叶域幅值最大值与曲率半径关系如图4所示。

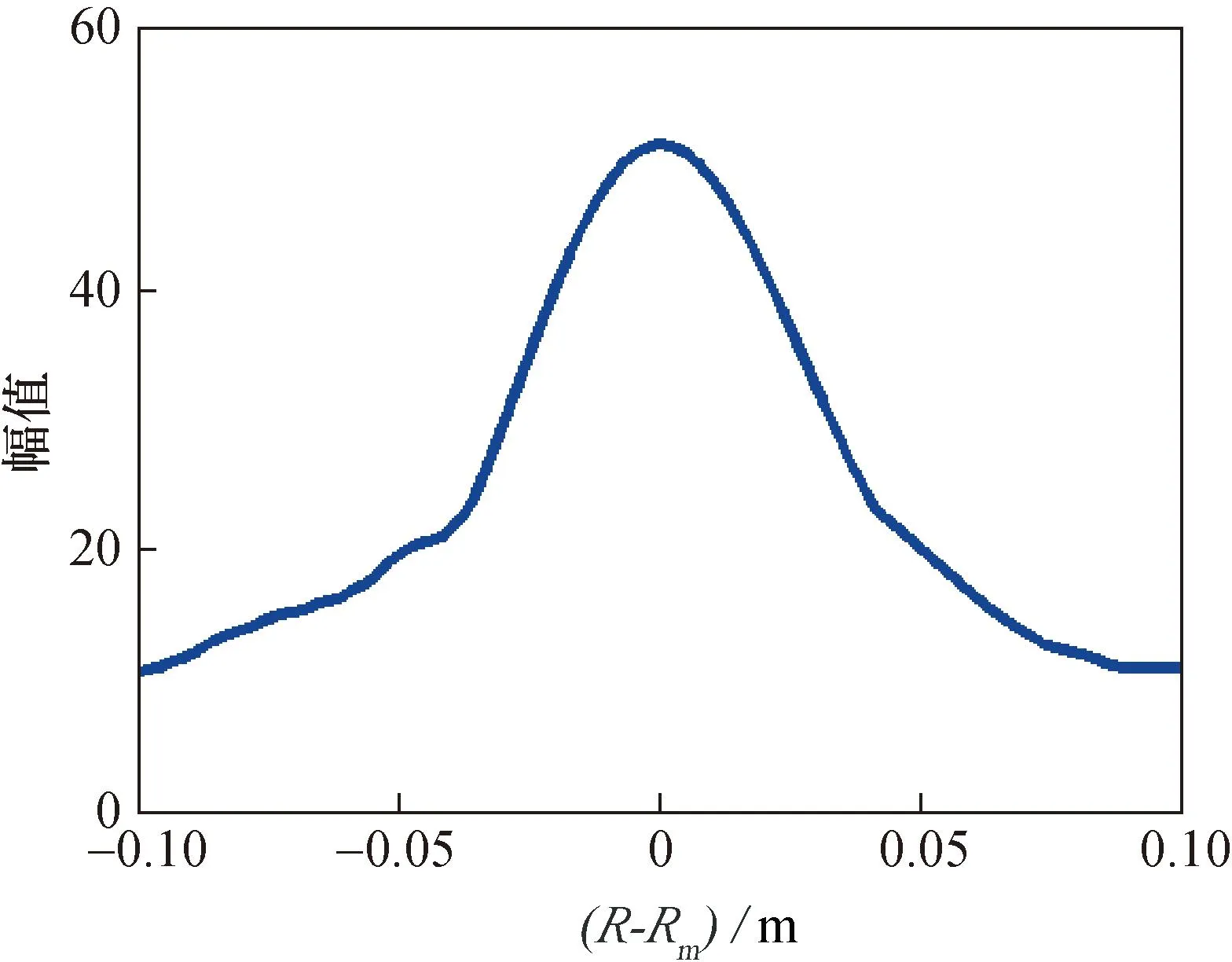
图4 分数傅里叶域幅值最大值与曲率半径关系

图4中Rm表示由αm计算的曲率半径。相应地,公式(13)可以写为

=a0+F1+F2

(14)

式中:n∈Z;F1是FM(R-Rm)奇次项之和;F2是FM(R-Rm)偶次项和;a0代表常数项。

图5为图4表示的原始分布与其多项式拟合分布对比图。

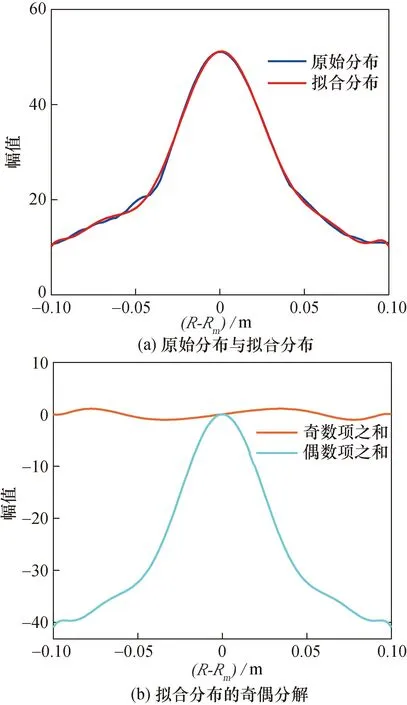
图5 图4表示的原始分布与其多项式拟合分布对比图

公式(14)中等式左端描述的分布规律与右端多项式拟合分布规律对比结果如图5(a)所示;多项式拟合分布基本符合原分布规律,奇次项之和如图5(b)中红色曲线所示,偶次项之和如图5(b)中蓝色曲线所示。

因此,根据最小二乘拟合原理,FM(R-Rm)可近似表达为

(15)

根据公式(15)可知,FM(R)关于Rm所在轴具有局部轴对称性。

本文提出基于三角收缩优化方法牛顿环参数估计效率,三角形收缩法原理如图6所示,其处理流程如下:

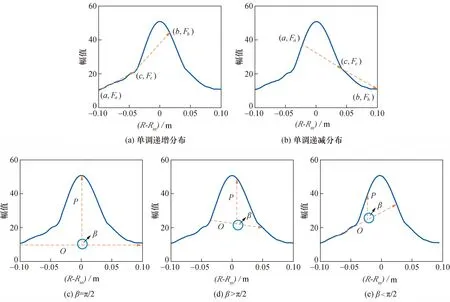
图6 三角形收缩法原理

(1) 设置初值

a,Fa=FM(a)

b,Fb=FM(b)

c=(a+b)/2,Fc=FM(c)

(16)

(2) 判断Fa,Fb,Fc大小,确定对称轴分布区间,

① 当FaFc>Fb时,如图6(b)所示,舍弃区间(c,b],保留区间[a,c]。

② 当FaFb时,连接3点构成三角形,定义角度β为两向量夹角可以描述为

(17)

式中:β∈[0,π];O代表(a,Fa)到(b,Fb);P代表(c,(Fa+Fb)/2)到(c,Fc)。

如图6(c)所示,当β=π/2时,在点c处与纵轴平行的线即为对称轴,c即为被测透镜的曲率半径;反之,当β≠π/2时,对于这种情况,需修正角度β;当β>π/2时,如图6(d)所示,舍弃区间(c,b],保留区间[a,c];当β<π/2时,如图6(e)所示,舍弃区间[a,c),保留区间[c,b];直到β=π/2或达到精度要求停止计算,从而通过对称轴的确定得到被测透镜曲率半径(或匹配旋转角)。

最后,可计算匹配旋转角对应的分数傅里叶变换,可以进一步获得包含在分数域幅值最大值位置对应的物理参数。

3 实 验

为了验证所提方法的有效性,在配有M1芯片的计算机上使用MATLAB R2021a根据公式(1)仿真牛顿环条纹图进行实验。实验中牛顿环背景强度I0=2,调制强度A=2,入射波波长λ=589 nm,被测透镜曲率半径为R=0.86 m,牛顿环环心坐标设值为条纹图中心位置。

对于不同像素尺寸的牛顿环条纹图,用本文方法估计曲率半径、环心坐标以及所需时间结果如表1所示。当条纹图尺寸小于640×640 pixels时,所提方法处理条纹图所需时间<1 s,而随着条纹图尺寸的增大,由表1可知,基于本文方法的曲率半径估计值相对误差减小,参数估计的精度也逐步提高,这主要与条纹图中包含的条纹级数相关。

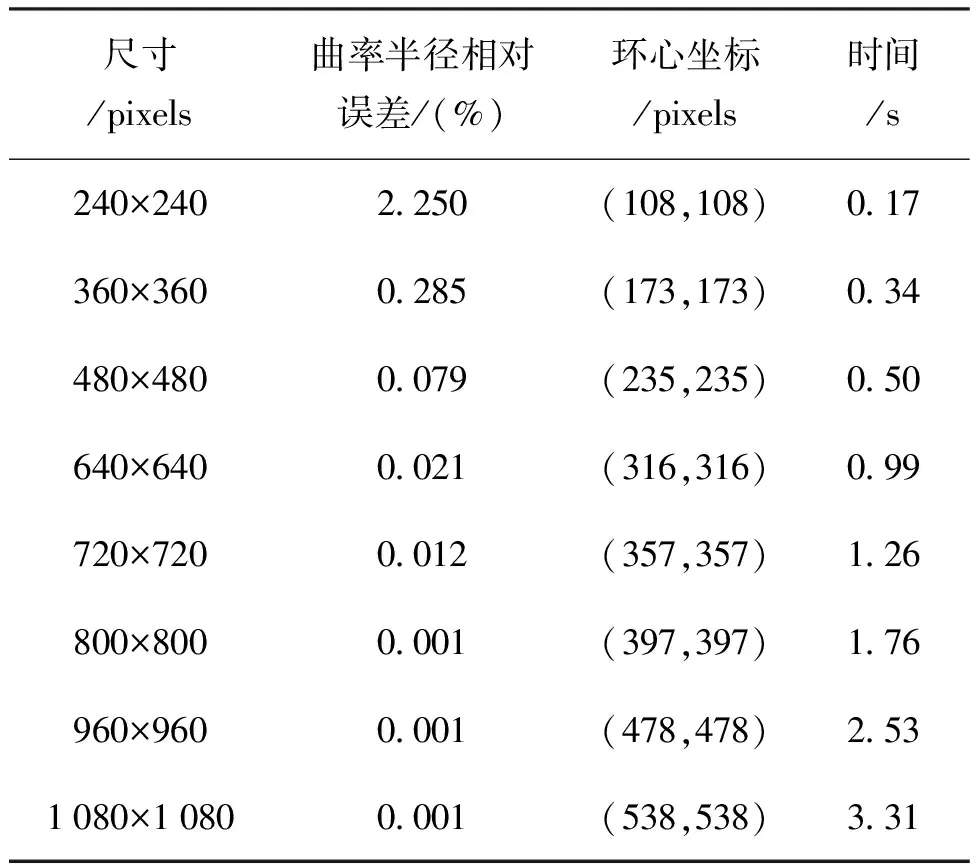
表1 不同尺寸牛顿环干涉条纹参数估计

以下列尺寸条纹图为例:240×240,480×480,720×720 pixels;条纹图及分数域幅值分布如图7所示。沿着图中箭头所示方向条纹图包含的级数增加,αm下分数域幅值分布能量聚集性更加明显,因此,包含在αm中的曲率半径估计更为精确。

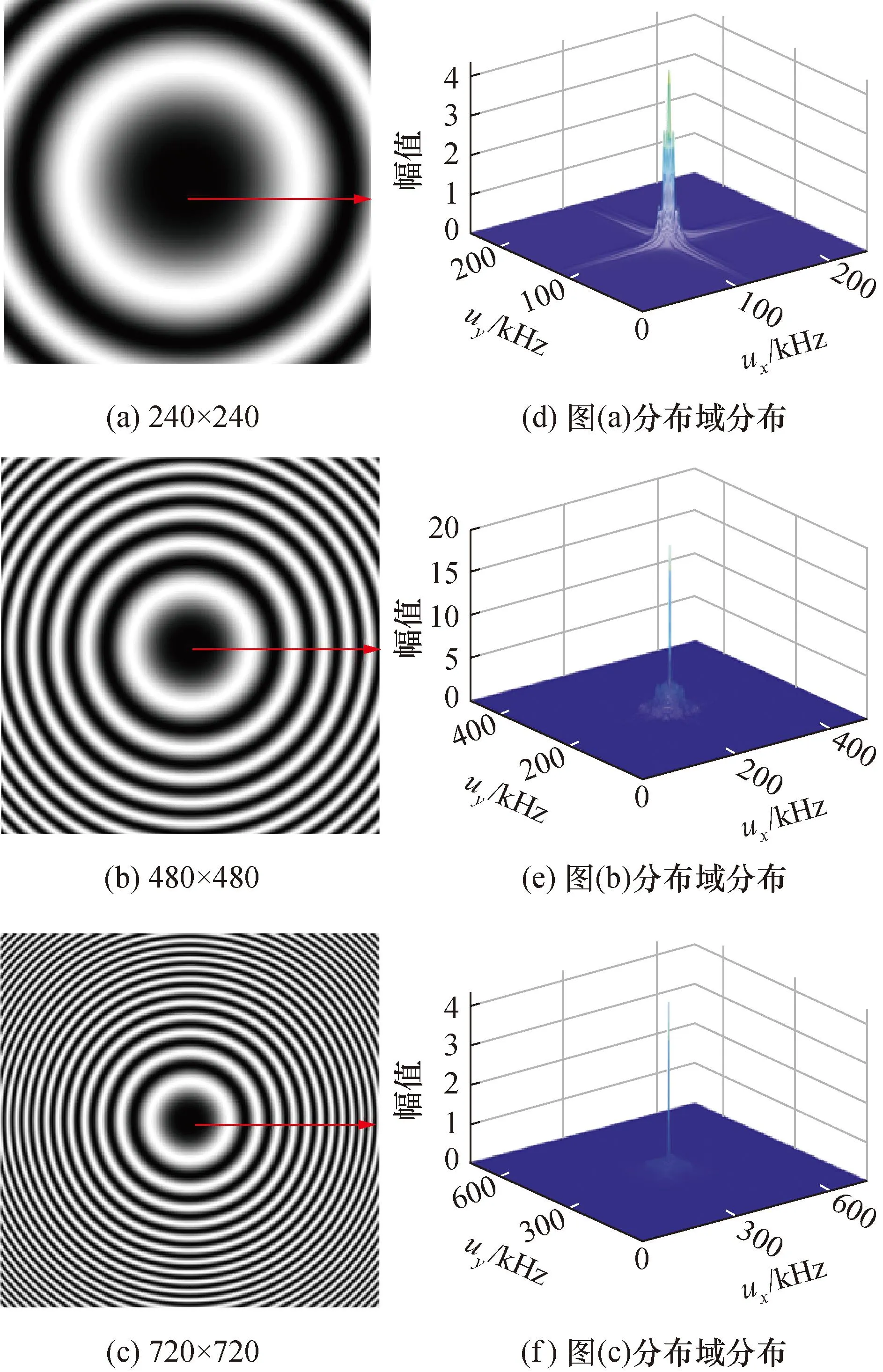
图7 不同尺寸牛顿环条纹图及其分数傅里叶域幅值分布

本文方法估计曲率半径的相对误差与条纹图级数的关系如图8所示。当条纹图尺寸增加,基于本文方法的参数估计时间增加,但仍可满足工程实际需求,以处理1 080×1 080 pixels的图像为例,估计值相对误差为0.001%,处理时间为3.31 s。

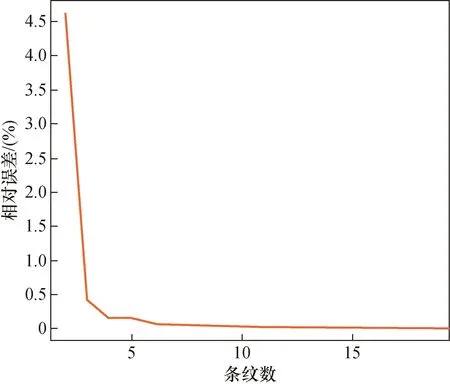
图8 曲率半径估计相对误差与条纹级数关系

为了进一步测试所提方法的抗噪能力,实验中通过对尺寸为720×720 pixels的牛顿环条纹图添加不同信噪比(SNR)的高斯噪声来验证。

为了保证相同的参数估计精度,传统分数傅里叶变换采用1×104步长均匀搜索方式估计高斯噪声污损牛顿环干涉条纹物理参数,相应的实验结果如表2所示。

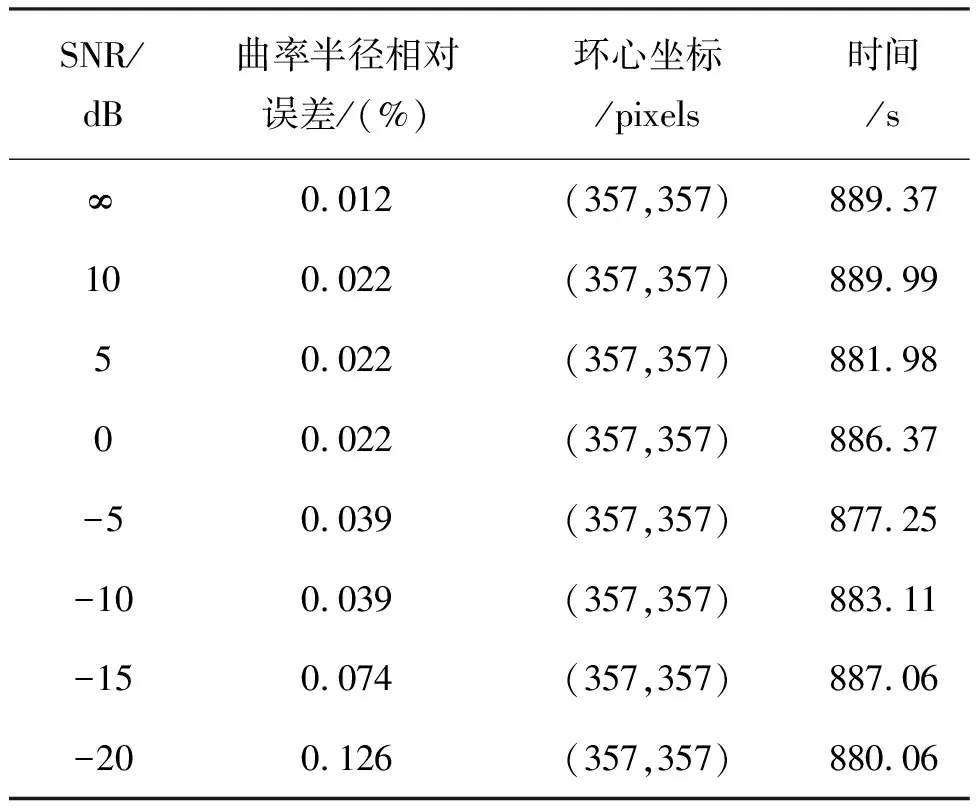
表2 高斯噪声污损下传统分数傅里叶变换估计牛顿环干涉条纹参数

本文方法估计高斯噪声污损牛顿环干涉条纹物理参数,实验结果如表3所示。

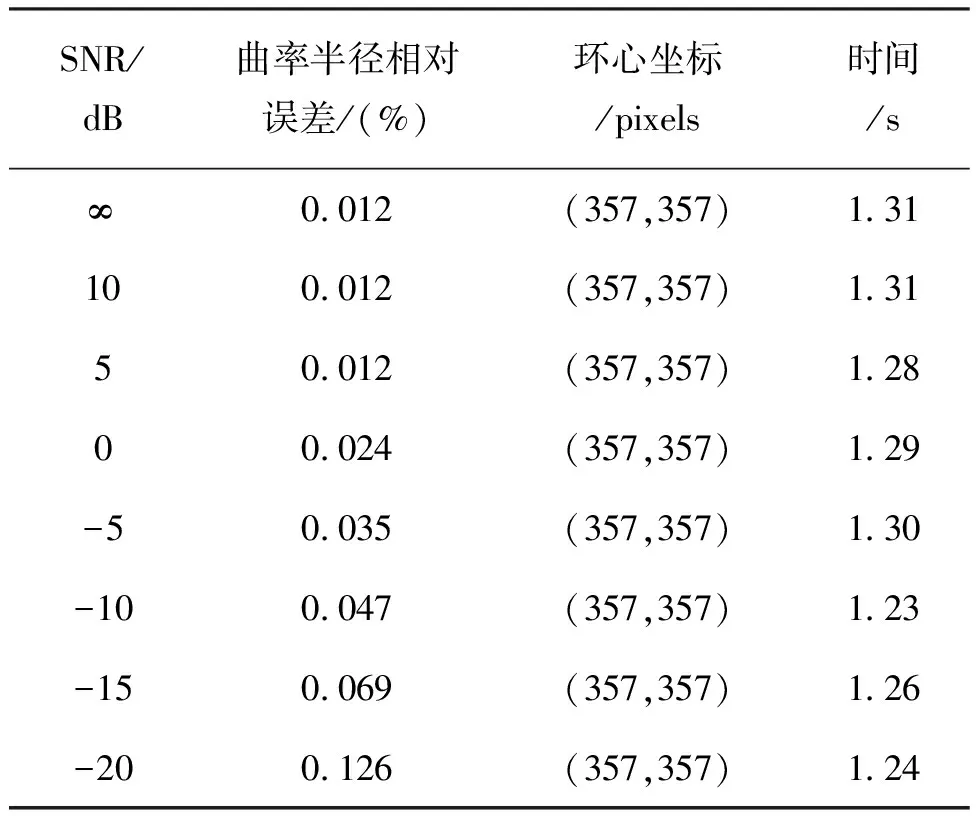
表3 高斯噪声污损下三角形收缩法估计牛顿环干涉条纹参数

实验结果表明:传统分数傅里叶变换和本文方法都具有很好的抗噪能力,但在保证同样估计精度的同时,传统分数傅里叶变换平均用时约为884 s,本文三角形收缩法平均用时约1.28 s。

高斯噪声污损牛顿环条纹图及其分数傅里叶域幅值分布如图9所示,对于SNR=-15的噪声污损条纹图,在分数域中其幅值分布仍可以实现很好的能量聚集性,相应地,采用本文方法估计曲率半径的相对误差为0.069%,处理时间为1.26 s。

图9 高斯噪声污损牛顿环条纹图及其分数傅里叶域幅值分布

此外,通过处理实际条纹图,本文方法的可行性也得到了验证,对于实际采集的640×480 pixels的牛顿环条纹图如图10所示,基于本文方法估计的曲率半径相对误差为0.067%,处理时间为0.64 s。

图10 实际牛顿环干涉条纹

4 结 论

针对传统分数傅里叶变换处理牛顿环参数估计时处理速度较慢这一问题,本文提出基于三角收缩优化的分数域处理方法。

通过建立不同旋转角α下牛顿环条纹图分数域幅值最大值分布模型,基于此模型利用初值构造三角形,通过判断三角形形状,从而确定α收缩区间并对三角形形状进行修正,直到所构造的三角形为等腰三角形,进而通过确定等腰三角形对称轴所在位置确定匹配旋转角αm,利用αm确定包含在其中的物理参数,如本文实验中的被测透镜曲率半径。该方法估计的曲率半径相对误差仿真结果最小可达0.001%,但是在处理实际条纹图时,其相对误差在1%左右,实际测量时限制该方法估计精度的因素包括:①因光照不均匀导致条纹图对比度下降引入的误差;②测量过程中存在像差以及被测元件变形等引入的系统误差;③实际条纹图处理时初值选取的较大偏差导致三角形模型判断失误而引入的误差。对上述误差源进行校准,可以进一步提升本文方法在估计牛顿环参数时的精度。

实验结果表明:本文方法具有可行性,对于图像尺寸小于640×640 pixels的条纹图,处理所需时间<1 s,随着图像尺寸增加,条纹图中包含的条纹数目增加,曲率半径估计值相对误差降低,而处理时间仍可满足工程实际需求,以处理1 080×1 080 pixels的图像为例,估计值相对误差为0.001%,处理时间为3.31 s。该方法估计720×720 pixels高斯噪声污损的牛顿环干涉条纹图像平均用时1.28s,约为传统分数傅里叶变换用时的1/700。