秉通法 悟通性 提升学科素养——以异构法在高考导数压轴题中的应用为例

陕西省榆林市吴堡中学 郭 蒙 (邮编:718200)

陕西省榆林市吴堡县教研室 薛小强 (邮编:718200)

《普通高中数学课程标准》(2017年版2020年修订)第88页在考试命题原则中强调:考查内容应围绕数学内容为主线,聚焦学生对重要数学概念、定理、方法、思想的理解和应用,强调基础性、综合性;注重数学本质、通性通法,淡化解题技巧.把握数学核心概念的本质,明晰什么是数学的通性通法[1].在文献[2]中,给出了一道导数压轴题的“异构”解法,知网中只有这一篇关于异构法的论文,篇幅只有一页半,老师们在这方面研究很少.异构法在处理导数压轴题时,是一把利器,很有必要研究,其应用非常广泛,将原复杂函数通过恒等变形转化为多个不同的简单函数的构造就是异构,主要用于不等式证明、不等式恒成立求参数的范围、零点等问题,本文主要研究其在高考导数压轴题中的应用.

1 两个切线不等式[1]

命题1ex-x-1≥0,(当且仅当x=0时取等号).

命题2x-lnx-1≥0,(当且仅当x=1时取等号).

评注这两个切线不等式在考试中应用时,需要证明,切线不等式在处理导数有关的压轴题时可起到化繁为简之效.

2 异构法在导数中的应用

2.1 证明不等式

1.指对异构

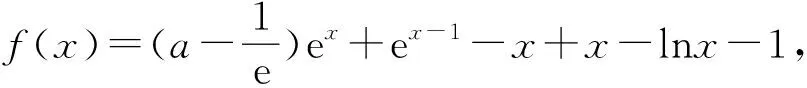
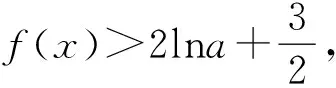
(2)指对+三角异构

例3证明:x2ex>(x+2)lnx+2sinx.

证明由题意知x>0,令g(x)=x2ex-(x+2)lnx-2sinx,则g(x)=x(ex+lnx-x-lnx-1)+(x2-lnx2-1)+(x-sinx)+1-sinx,由命题1、2,知ex+lnx-x-lnx-1≥0,当且仅当x+lnx=0时取等号,x2-lnx2-1≥0,当且仅当x=1时取等号.由x>0,知x-sinx>0,由于1-sinx≥0,因此g(x)>0恒成立,故原不等式成立.

评注当xmex与lnx再加上sinx时,利用对数恒等式、g(x)=x-sinx和命题1、2一起进行异构,由于取等条件不一致,故一定恒大于0.

2.2 不等式求参

(1)指对求参

例4(2020年新高考1卷)已知函数f(x)=aex-1-lnx+lna,若f(x)≥1,求a的取值范围.

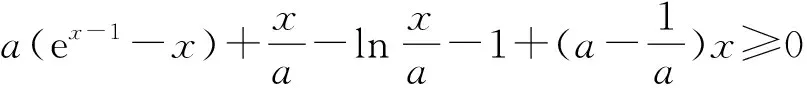
评注此题用到了对数恒等式b=elnb及切线不等式,此切线不等式在考试中经常用到.

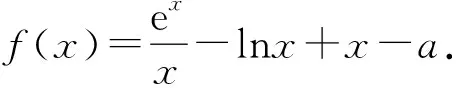
评注异构解法非常精彩,借助命题1、2将复杂函数转化为几个常见函数,大大简化了解题过程.

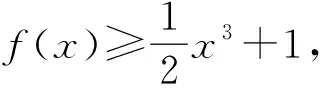
图1

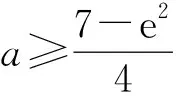
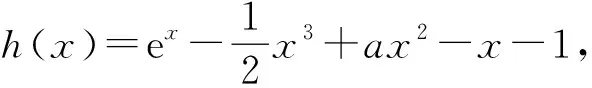
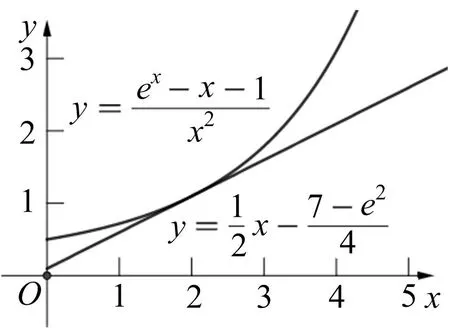
图2

从以上解题过程得到以下结论:

推论1已知h(p(x))+h(q(x))+g(x)≥0恒成立,且取等均在x=x0处,若h(p(x))+h(q(x))+g(x)+mφ(x)≥0,当φ(x)在定义域内恒正,可以利用x=x0,证明m<0矛盾.

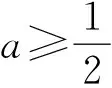
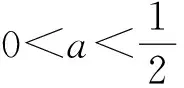
图3

评注本题用到了常用的方法对数单身狗以及飘带不等式,将函数转化为多个非负函数的和的形式,利用原函数的非负性,求出参数的范围,矛盾点(矛盾区间)的取法除了对原函数进行放缩,还可以利用导函数或者隐零点放缩法来取矛盾点(矛盾区间).

(2)三角求参

所以当a≤3时,m(x)>0显然成立.

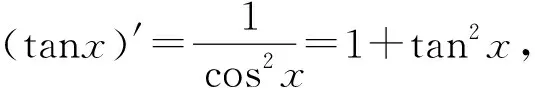
推论2若h(p(x))+h(q(x))+g(x)≥0恒成立,且取等均在x=x0处,若h(p(x))+h(q(x))+g(x)+mφ(x)≥0,当x0在定义域内为0且,φ(x0)=0,则求导,利用导函数在x=x0处小于0,找到矛盾区间,证明m<0矛盾,也可以将原函数直接放缩,找到矛盾点,证明m<0矛盾.

2.3 零点问题

例9已知函数f(x)=ex-1,g(x)=asinx,a∈R.试讨论f(x)-g(x)在x∈[0,π]上的零点个数.

解析令h(x)=f(x)-g(x)=ex-1-asinx=ex-x-1+a(x-sinx)+(1-a)x.h′(x)=ex-acosx,h″(x)=ex+asinx.

(1)当a≤0时,ex-1≥0,-asinx≥0,因此h(x)≥0,当且仅当x=0时取等号,故h(x)仅有一个零点.

(2)当0

(3)当a>1时,h″(x)>0,h′(x)在x∈[0,π]上单调递增,h′(0)=1-a<0,h′(π)=eπ+a>0,因此存在唯一x0∈(0,π),使得h′(x0)=0,当x∈(0,x0),h′(x)<0,h(x)单调递减,h(0)=0,h(x0)0,h(x)单调递增,h(π)=eπ-1>0,因此存在唯一x1∈(x0,π),使得h(x1)=0,故h(x)在[0,π]上存在0,x12个零点.

综上,a≤1时,有1个零点,a>1有2个零点.

评注利用异构法可以处理零点问题,当0

异构是相对于同构[3]而言,同构法可以利用函数的单调性和最值,但异构必需建立在保值性的基础上,异构法难于构造,要求读者十分熟悉常见不等式,需要多加练习,同构与异构的本质其实就是分类讨论的思想,异构第一步在于恒等变形,第二步保值证明,对于求参数问题,还要找矛盾点(矛盾区间),异构法是解决导数压轴题的一把利器,是一种通法,异构法在极值点偏移问题方面应用也很广泛,师生应重视通性通法,重视知识的形成过程,多反思,体会出题人的意图,明确考查的知识与能力,归纳试题反映的通性规律,落实数学学科核心素养,希望本文对读者的学习有一定的启发作用.