实用化态制备误差容忍参考系无关量子密钥分发协议*

周阳 马啸 周星宇 张春辉 王琴†

1) (南京邮电大学,量子信息技术研究所,南京 210003)

2) (南京邮电大学,宽带无线通信与传感网教育部重点实验室,南京 210003)

1 引言

量子密钥分发(quantum key distribution,QKD)可以在两个远距离用户Alice和Bob之间形成一致密钥,其安全性基于量子力学的基本原理,且已被证明具有信息论安全性[1,2].经过几十年的发展,QKD理论已经比较成熟,且在不同的场景下得到了实验验证,如基于光纤的QKD[3-6]和自由空间信道QKD[7,8].在上面提到的大多数QKD系统中,Alice和Bob之间需要一个共享的参考系,而实时校准参考系在一定程度上增加了系统的成本并降低了性能.幸运的是,参考系无关(referenceframe-independent,RFI)QKD协议[9]的概念被提出,克服了参考系漂移问题,从而受到了广泛的关注.

实际器件特性的不理想使得QKD的理论和实践之间存在一定矛盾.在实际QKD系统中,存在光源缺陷和探测端缺陷等问题,使得系统的安全性降低.针对光源端态制备误差问题,2014年,在GLLP协议[10]的基础上,Tamaki等[11]提出了一种态制备误差容忍(loss tolerant,LT)的QKD协议.随后,出现了一系列与光源安全性相关的工作[12-15],其中,2015年Wang等[12]将损耗容忍方案与参考系无关协议结合,有效提升了RFI QKD协议的光源安全性.

但除了源端缺陷之外,由于探测器固有的半导体结构缺陷,在正常的探测信号之后也容易产生虚假的非光子探测脉冲输出,会造成错误的计数,也就是后脉冲效应[16-18],从而导致误码率增大.同时,单光子探测器在探测事件发生后会进入一段“恢复期”,在此期间,探测器不会对其他的光脉冲响应,这将带来死时间效应[19-21].对于一般的QKD系统,死时间和后脉冲效应可以忽略不计,但随着系统重复频率的增大,尤其进入千兆赫兹,这种假设就不再合理.基于以上问题,本文提出了一种同时考虑光源端和探测器缺陷的实用化态制备误差容忍参考系无关(loss tolerant reference-frame-independent,LT-RFI) QKD协议,并且以三强度诱骗态方案[22](信号态+弱诱骗态+真空态)为例进行相应的模型分析与数值仿真计算.该协议通过利用虚拟态方法来估算相位误码率,显著降低了态制备缺陷对密钥率的影响,这意味着本文的协议在传输过程中能够更有效地防止由于态制备误差而导致的信息损失.此外,通过刻画后脉冲和死时间对密钥率带来的影响,本文的协议还表现出更高的鲁棒性,能够有效应对探测器端的缺陷问题.

2 理论模型

在实际的量子密钥分发系统中,由于器件的不完美,不可避免地存在量子态制备误差、后脉冲效应与死时间效应.针对3种缺陷,本文提出了同时考虑光源和探测器缺陷的实用性态制备误差容忍参考系无关量子密钥分发协议,该协议通过将态制备误差、后脉冲与死时间等缺陷分别进行建模和刻画,并对QKD系统重新进行了安全性分析证明,使得该模型的结果可以对误差具有较好的容忍性能,模型的鲁棒性得以增强.

下面以相位编码的QKD系统为例进行具体模型介绍.由于现实环境下编码系统在态制备过程存在一定的缺陷,制备出的量子态与理想的量子态之间存在一定偏差,因此考虑态制备误差时,Alice对量子态中的误差刻画如下:

其中δ1和δ2表示由于衰减器或强度调制器不理想造成的态制备误差,δ3和δ4表示由于分束器不理想造成的误差,θ1和θ2表示由相位调制器不理想造成的偏差.

在RFI协议之中,Eve获取的信息量由IE表示为

其中

接下来,使用虚拟协议[23]来更紧致估计4组不同基矢下的误码率:EXX,EXY,EYX,EYY.以误码率EXX为例,其表征为虚拟协议中X基下的比特误码率,表达式如下:

其中pjX,vir表示发送Alice在系统B发送虚拟态的概率;1/4表示Bob选择X基矢测量的概率;qsX|t=表示泡利矩阵的传输率,且t∈{Id,X,Y,Z};表示Eve窃听的测量算符.

对于虚拟态的发送概率pjX,vir,其可表示为p0(1)X,vir={1±sin[(δ1+δ2)/2]}/2,而对于泡利矩阵的传输率qsX|t,与真实量子态的计数率满足如下关系:

由此,可以求得相位误码率EXX,其他相位误码率EXY,EYX,EYY求解方法相同.以上,可精准求得窃听者Eve在量子密钥分发过程中获取的信息量.

由于在接收端有两个探测器,因此协议有效的探测事件分为两种情况: 两个探测器同时响应或者只有一个探测器响应.首先考虑探测端带来的后脉冲效应,探测器的响应正确(错误)的概率以及两个探测器同时响应的概率满足如下表达式:

其中Pdc表示暗计数率,Pap表示后脉冲概率.

当使用弱相干态(weak coherent state,WCS)光源时,认为只有一个探测器响应且测得正确的概率为、只有一个探测器响应但测得错误的概率为Done,×、两个探测器同时响应的概率为Dtwo.相应的表达式如下:

其中η表示系统的总透射率,Alice发送量子态 |ϕ0Z〉且Bob使用Z基测量得到正确比特值0的概率为C0Z|0Z,错误结果的概率为C1Z|0Z.

结合诱骗态方法,可以得到平均光子数为λ的增益为

其中λ∈{µ,v},a=ηCn,sα|jγ,D=1-Pdc.Vn,sα|jγ表示Alice发送量子态 |ϕjγ〉且Bob选择α基测量得到s比特的条件概率,s,j∈{0,1},α,γ∈{X,Y,Z}.其表达式为

其中ϑsα|jγ=(1+ηCsα|jγ-η)n-(1-ηCsα|jγ)n-(1-Pdc)(1-η)n.

当考虑死时间效应时,Alice制备 |jγ〉量子态并发送平均光子数为λ的脉冲,然后Bob使用 |sα〉量子态测量的探测概率为Pλ,sα|jγ=cdtPλPγ|λPαQλ,sα|jγ.其中,Pλ表示Alice发送λ强度脉冲的概率,Pγ|λ表示Alice发送λ强度脉冲条件下选择γ基的概率,Pα表示Alice选择α基矢的概率.cdt表示死时间效应引起的修正系数,满足关系式:

其中F为系统重复频率,τdt为死时间大小,为基于ξ基下λ强度的探测效率.

根据信号态µ、诱骗态v的增益,可以得到单光子计数率的下限,从而得到Z基下的单光子增益和比特误码率:

Z基下的整体增益QZ和比特误码率eZ,满足关系式:

结合以上参数和公式,代入下面密钥率公式,即可得到安全密钥率[12]大小:

其中,f为系统纠错系数;IE为Eve获取的信息量.通过对上述参数求解,可以计算出最终密钥.

3 数值仿真结果及分析讨论

在数值仿真中,使用合理的实验系统参数[12],如表1所列.

表1 基于后脉冲效应和死时间效应的LT-RFI协议仿真参数列表Table 1.Parameter list used in simulation of LT-RFI protocol based on after-pulse effect and dead time effect.

为了更直观地说明光源端和探测端不同设备缺陷对LT-RFI协议的影响,基于WCS且考虑有限长效应的RFI协议的密钥率随距离的变化曲线如图1所示.其中,实线表示不考虑态制备误差容忍下RFI协议的结果,虚线对应LT-RFI协议的结果.

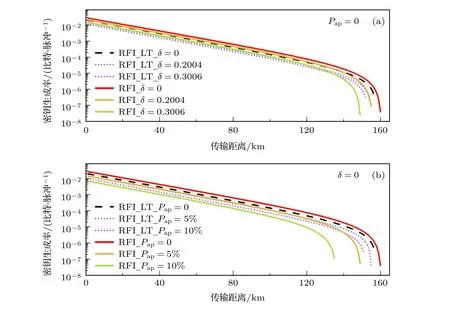
图1 (a) 基于态制备缺陷 δ 的RFI协议以及LT-RFI协议的密钥生成率图;(b)基于后脉冲效应 Pap 的RFI协议以及LT-RFI协议的密钥生成率图Fig.1.(a) Key generation rates of the RFI protocol and LT-RFI protocol based on state preparation flaws δ;(b) the key generation rates of the RFI protocol and LT-RFI protocol based afterpulse effect Pap.

图1基于RFI 协议和LT-RFI协议分别比较了两种不同缺陷条件下的安全密钥率.图1(a),(b)中从上到下实线分别依次表示δ(Pap) 为0(0),0.2004(5%)和0.3006(10%)的RFI 协议的安全密钥率曲线;从上到下的折点线则分别依次代表与对应实线δ(Pap)相同的LT-RFI协议的安全密钥率曲线.当δ=0.3006时,与理想状态相比,与传统RFI不同,在估算不同基的比特误码率时,不是直接对不完美态进行投影测量计算,而是通过引入虚拟态、虚拟协议和过渡矩阵,对测量过程做了一定变换和优化处理,原理上降低了态制备误差对估算结果的影响.但是,在此过程中不可避免地增加了一些统计量参与估算,在考虑有限长效应时,在一定程度上增加了有限长效应的影响,故在态制备误差为0时,LT协议的码率相比于传统RFI协议有一定的下降;随着态制备误差的增大,LT协议的鲁棒性和优势才逐渐显示出来.与理想状态相比(δ=0.3006),LT-RFI(RFI)协议的密钥率下降了约1/2(4/5),最远传输距离减小了5(12) km.

同样,当Pap=10%时,LT-RFI (RFI)协议比后脉冲大小为0条件下的密钥率下降了1/2 (3/4),最远传输距离减小了6 (25) km.值得注意的是,与传统RFI不同,LT-RFI在估算不同基的单光子比特误码率时,不是直接使用对不完美态做投影测量的结果进行计算,而是通过引入虚拟态、虚拟协议和传输矩阵,对测量过程进行一定变换和优化处理,原理上降低了态制备误差对估算结果的影响.但是,在此过程中不可避免地增加了一些统计量参与估算过程,因此,在一定程度上增加了有限长效应的影响,故在态制备误差为0时,LT协议的码率相比于传统RFI协议有一定下降,于是图1中出现态制备误差为0时,红色实线略高于黑色虚线的现象;但随着态制备误差的增大,LT协议的鲁棒性和优势又逐渐显示出来.

图2给出了同时考虑态制备缺陷和后脉冲效应条件下的密钥率结果.当态制备缺陷δ=0.2004,Pap=5%时,RFI协议的密钥率比理想情况(δ=0,Pap=0)下该协议的密钥率降低了67%,最远传输距离减小了18 km.而我们提出的实用性LTRFI协议的密钥率仅仅降低了50%,最远传输距离减小5 km.此外,当δ=0.3006,Pap=10%时,RFI协议的密钥率比理想情况下的密钥率降低了一个数量级以上,最远传输距离更是急剧减小45 km.与之相比,LT-RFI协议的密钥率虽然降低了70%,但最远传输距离仅仅减小了10 km.通过以上结果可以得出,基于诱骗态方法的传统RFI协议虽然对态制备缺陷和后脉冲效应具有一定的鲁棒性,但依旧不如LT-RFI协议.主要由于与传统的RFI协议相比,LT-RFI协议除了对态制备误差具有鲁棒性,对探测端的后脉冲效应也具有良好的鲁棒性.主要原因与上面类似,LT-RFI协议通过引入虚拟态、虚拟协议和传输矩阵,对测量过程做了一定变换和优化处理,原理上降低了测量端的不完美对估算结果的影响,从而使得Eve获取的信息量降低,从而具有更好的鲁棒性.

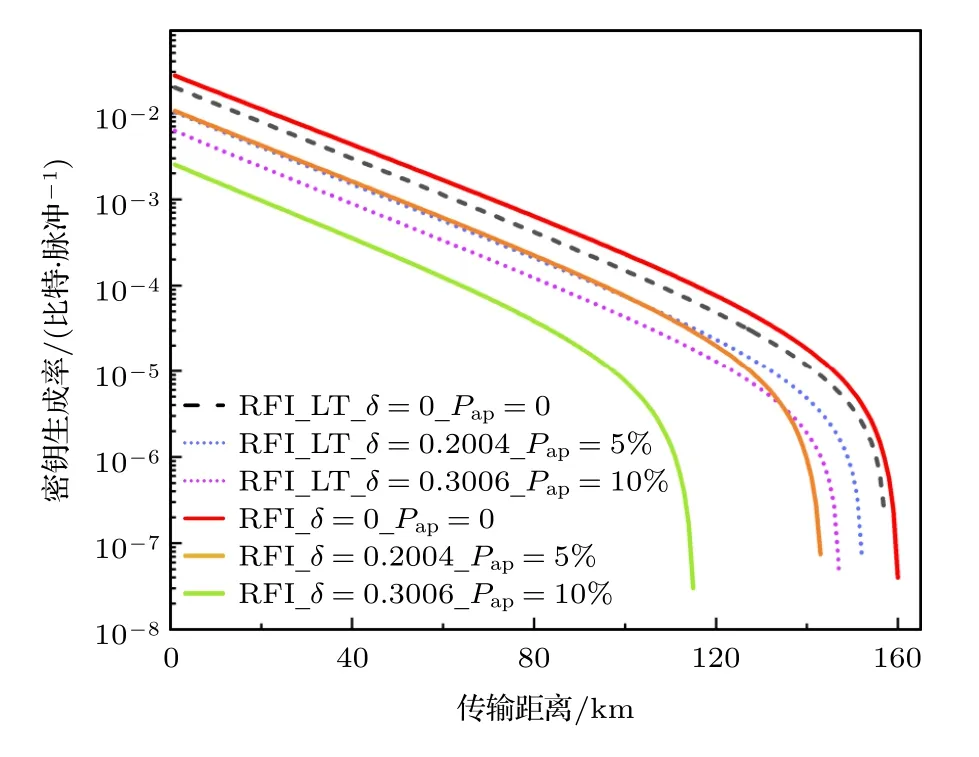
图2 基于态制备缺陷和后脉冲效应的RFI 协议以及LT-RFI协议的密钥生成率图Fig.2.Key generation rates of the RFI protocol and LTRFI protocol based on state preparation flaws and afterpulse effect.

如图3所示,当不考虑态制备缺陷时,RFI协议中Eve获取的信息量明显要高于LT-RFI协议对应的Eve获取的信息量.在距离相同的条件下,随着态制备缺陷δ和后脉冲概率Pap的增大,前者显著增大,而LT-RFI协议对应的Eve获取的信息量仅略微增加.这是由于在LT-RFI协议中使用的虚拟比特误密钥率更加紧致地估计了相位误密钥率,进而更加紧致地估计Eve获取的信息量.

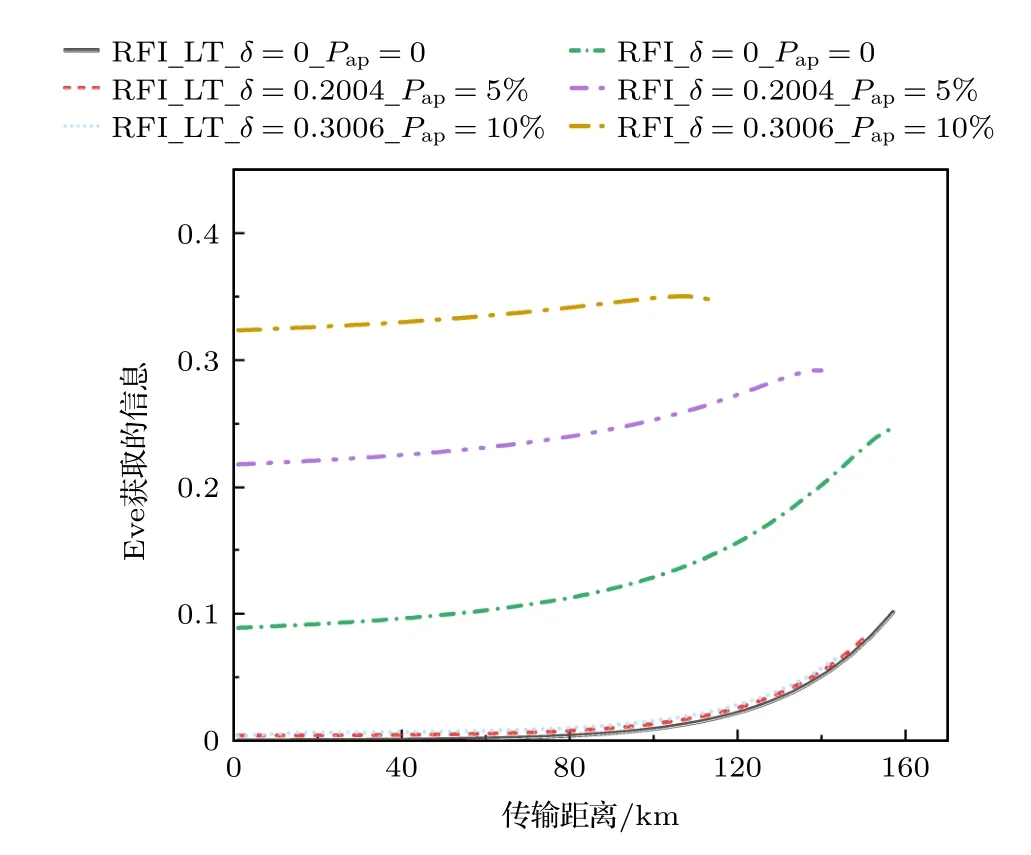
图3 基于态制备缺陷和后脉冲效应的RFI 协议与LT-RFI协议的Eve获取的信息量Fig.3.Information leakage to Eve of the RFI protocols and LT-RFI protocols based on state preparation flaws and after-pulse effect.

为了进一步展示不同设备缺陷同时对LTRFI协议造成的影响,下面给出了基于态制备缺陷、后脉冲效应和死时间效应的LT-RFI 协议的密钥率随距离变化的曲线,如图4所示.其中,黑色实线表示3种设备缺陷都为0的密钥率结果,红色实线与绿色虚线表示δ=0.2004,Pap=5%但死时间大小不同的密钥率结果.为了更好地表现LT-RFI协议的性能,对3种缺陷进行放大(δ=0.3006,Pap=10%且τdt=1 μs)并对密钥率进行仿真(紫色虚线).结果表明,当同时考虑这3种设备缺陷时,LT-RFI协议的传输距离和安全密钥率有不同程度的下降.通过对比红色实线与绿色虚线发现死时间效应会导致短距离内的密钥率大幅下降,但这种影响会随着距离的增大而下降,因此最远传输距离下的密钥率几乎相同.此外,与绿色虚线相比,紫色虚线的3种缺陷分别是前者的1.5倍、2倍与50倍,后者的密钥率减小了一个数量级,但最远传输距离仅减小5 km.因此,对于LT-RFI协议,死时间效应只是在近距离时进一步降低密钥率,而没有影响最远传输距离.

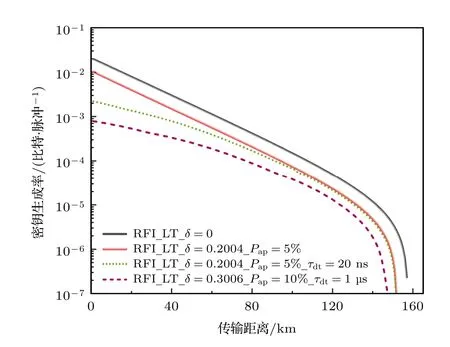
图4 基于不同设备缺陷的RFI协议以及LT-RFI协议密钥生成率图Fig.4.Key generation rates of the RFI protocol and LTRFI protocol based on different defects in equipments.

4 结论

本文提出了一种同时考虑光源端与探测器缺陷的实用化态制备误差容忍参考系无关QKD协议.本文首先考虑了QKD系统中光源的不完美性,将发送端制备态误差大小进行刻画并代入安全性分析之中,并考虑了损耗容忍方法.然后进一步考虑了探测器的不完美性(后脉冲效应和死时间效应)对该协议的影响.以三强度诱骗态方法为例来进行模型构建和参数估计方法介绍,同时开展相应数值仿真计算.结果表明,本文提出的协议通过利用虚拟态测量相位误密钥率不仅减小了态制备缺陷对密钥率的影响,还对探测器端的缺陷(后脉冲效应、死时间效应)更具有鲁棒性.

需要指出,本文对RFI QKD的分析中,在接收端使用了两个单光子探测器来构建模型,为了简化计算,在仿真中假设两个探测器的性能完全一致.倘若两个探测器性能不一致,如探测效率和暗计数等,则可能会引入一定安全隐患,进而降低整个QKD系统的实际性能[24,25].当然,在实际应用中,不同探测器的性能不可避免存在一定差异,是需要实际考虑和解决的问题,也将成为我们后继的工作重点之一.本方法还可以拓展到其他安全性等级更高的量子密钥分发协议,如与测量设备无关的量子密钥分发协议[26-30]以及双场量子密钥分发[31,32]等,进一步降低实用化进程中QKD系统因器件缺陷所带来的不利影响.因此,本文工作将对QKD系统的实用化起到一定推进作用.