基于可见光定位技术的车联网车辆位姿监测方法*

谢心月，邹德岳**，刘源

（1.大连理工大学信息与通信工程学院，辽宁 大连 116024；2.中国计量科学研究院，北京 100000）

0 引言

随着车联网技术的不断发展，智能交通监测成为解决交通拥堵、提高交通安全和效率的重要手段，而对车辆位置和姿态的准确监测成为实现智能交通和车辆互联的关键[1-2]。然而，在城市中的一些复杂封闭环境，如城市峡谷、隧道、地下停车场等，GNSS（Global Navigation Satellite System，全球导航卫星系统）信号受到阻隔，导致定位效果不佳，甚至完全失效。其他可行的定位方案，如Wi-Fi和超宽带雷达，往往在城市环境中部署困难[3-4]。此外，纯粹依靠惯性导航的定位方法容易随时间累积误差[5-7]。这些问题限制了车联网技术的发展和应用，也给城市交通管理带来了挑战。为了解决这些问题，提出将VLP（Visible Light Positioning，可见光定位）技术[8-9]应用于车联网中，以解决车辆定位问题。VLP 技术不依赖于GNSS，可以在复杂城市环境中独立工作，提供持续稳定的定位服务。本研究旨在探索VLP 技术在车联网智能交通监测中的应用，为解决城市交通问题提供技术支持。

目前存在许多VLP 算法，但难以应用在上述的封闭环境里：指纹算法适用于固定的室内场景，且无法实现姿态角的跟踪[10-11]；AOA（Angle of Arrival，到达角度）算法则依赖于接收器对入射光角的检测精度和光源数量[12-13]；TOA（Time of Arrival，到达时间）算法则需要高度精确的时间同步[14-15]；RSS（Received Signal Strength，信号接收强度）算法取决于接收器对光强的准确识别，以及准确的光传播信道模型，且容易受到灯光反射等因素的影响[16-17]。总之，这些算法在光信号传播距离较短且接收稳定的室内环境中表现出色，但在城市环境中的效果不尽如人意。因此，为实现高精度的车辆位姿测量，设计了一种多传感器数据融合方案，以提高VLP 在车辆位姿测量环境下的定位精度和鲁棒性。

最近的学术研究对VLP 算法提出了一些改进方案，但无法完全解决VLP 在复杂环境下的定位挑战：将EKF（Extend Kalman Filter，扩展卡尔曼滤波器）应用到VLP 中以提高定位的鲁棒性，但VLP 系统的非线性特点会导致复杂的雅可比矩阵计算[18-19]；在UKF（Unscented Kalman Filter，无噪声卡尔曼滤波器）中使用RSS 模型会继承RSS 算法易受环境影响的缺点[20]。因此，为实现高精度的车辆定位，在之前的研究[21]的基础上，提出了一种改进的VLP 算法，使用单目相机和IMU（Inertial Measurement Unit，惯性测量单元），基于刚体运动模型来使用UKF 融合单目相机的图像数据和IMU 的数据计算得到无人载具的位置和姿态角。通过仿真模拟，验证了该算法在精度和鲁棒性方面的出色性能。

1 理论分析

1.1 投影模型

投影模型如下图所示（见图1）：被监测车辆携带三个可见光光源（以下简称LED）以及IMU，三个LED 分别标记为此外，使用相机捕获车辆上LED 的图像，它的光心记为Oc。LED 排布不受限制，但需确定各个LED 灯之间的相对位置。

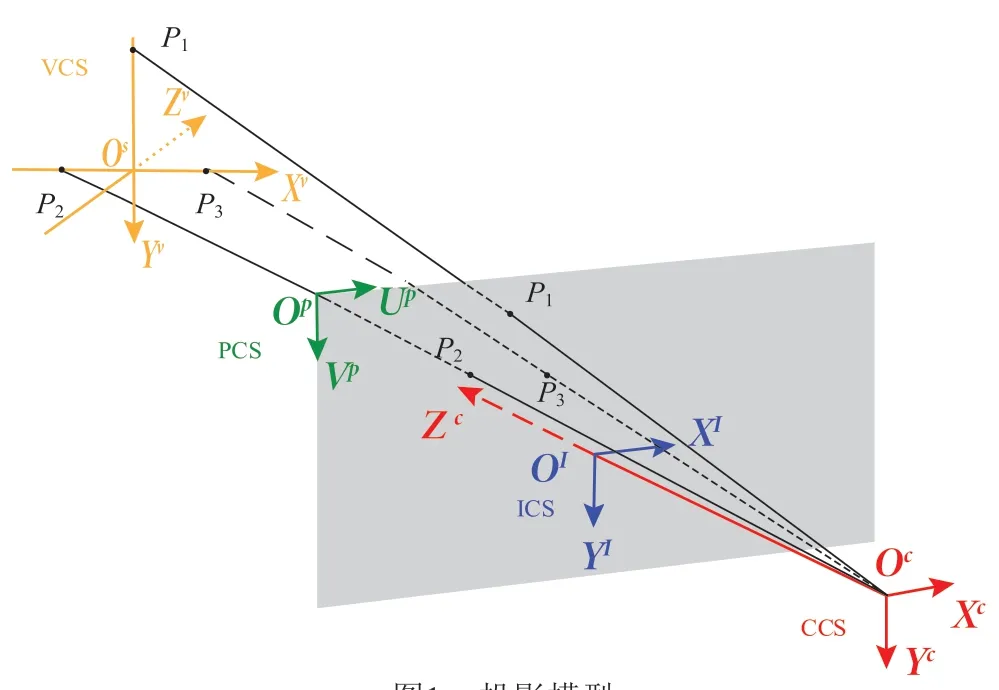
图1 投影模型

在图1 中，建立四个坐标系统：CCS（Camera Coordinate System，相机坐标系统），该坐标系统的原点位于相机的光心，其Z 轴指向被监测车辆；ICS（Image Coordinate System，图像坐标系统），该坐标系统的原点位于相机成像平面的中心，用于描述LED 在图像上的坐标；PCS（Pixel Plane Coordinate System，像素平面坐标系统），该坐标系统的原点位于成像平面的左上角，用于描述LED 的像素坐标；VCS（Vehicle Coordinate System，车辆坐标系统），该坐标系统的原点位于LED 图案中心，且初始化的各轴方向与CCS 坐标系相同，用于描述无人船的位置和姿态。在CCS、ICS 和PCS 中，坐标轴Xc、Xi和Up相 互 平 行，Yc、YI和Vp相 互 平 行。Oc到OI的 距离即为相机焦距。其中，为各个LED 在VCS 中的坐标；为 各个LED 在CCS 中的坐标；为各个LED 在ICS 中的坐标；为各个LED 在PCS 中的坐标，这些坐标可以从相机的图像中获得。

1.2 VLP算法

（1）传感器输入

对于过程方程的输入，车辆携带一个IMU，可以跟踪VCS 相对CCS 在X 轴、Y 轴和Z 轴上的姿态角变化,分别记为γ、β和α。但是，由于β存在累积误差，该算法不将β作为输入，而将其作为未知数进行估计，这样既利用了惯性测量传感器的数据,又尽量避免了累积误差的影响。对于观测方程的输入，则使用相机的图像数据中的

（2）状态向量

在算法中，第k-1 个计算周期对应的状态向量为：

（3）过程方程

过程方程(2)的作用是从第k-1个计算周期的状态预测第k个计算周期的状态，计算公式如下：

其中ωk为预测噪声，Rk表示CCS 与VCS 之间的旋转矩阵，计算公式如下：

在本文中，将式(3)简写为式(4)：

（4）测量方程

（5）无迹卡尔曼滤波器

在本节中，将在UKF 中使用第（1）～（4）点的内容，使得UKF 可以正确地计算状态向量。

在第k计算周期，使用式(7)计算第k-1 周期的最优状态的sigma点，其中n表示状态元素的数量，Xk-1表示k-1 周期的最优状态，表示k-1 周期的最优状态的sigma 点。

其中，Qk-1为Xk-1的协方差矩阵，λ是对角线因子，计算公式如下：

其中，L为测量噪声的协方差矩阵。

进一步地，就可以联合式(17) 和式(18) 计算出卡尔曼增益Kk，计算公式如下所示：

2 算法仿真与结果分析

2.1 仿真参数和方法介绍

在该算法的测试中，相机的分辨率为2 280×1 080，单位为像素；相机的内参矩阵Ain已提前标定完成，如下所示：

算法初始化时，VCS 与CCS 方向一致并位于CCS的Z 轴正前方3 m 处。测试时，生成一个随机的车辆轨迹，LED 坐标随着车辆的在轨迹中的位置和姿态也随机变化，且保证每次的轨迹与相机的距离从0 m 开始直至最大120 m。

通过两个误差指标来评估算法性能：定位误差和姿态角误差，分别对应状态向量中的和β。定位误差定义为算法状态向量中的与随机轨迹中的的欧氏距离，而姿态角误差则定义为算法状态向量中的β与随机轨迹中的β的累积差值。在测试中，将LED 组成的图案固定为正三角形，设置不同的边长（单位：米）和图像噪声（单位：像素）水平对这两个误差的影响，以探讨不同环境条件下算法性能的变化。

2.2 仿真结果与分析

首先，设定不同的LED 图案边长L，并且将像素噪声设置为服从均值为0，标准差为1 的高斯分布N(0,1)，以测试不同L对算法的定位误差和姿态角误差的影响。在0 到120 m 的随即轨迹中，在L的值设定为3 m 时，从定位误差的CDF（Cumulative Distribution Functions，累积分布函数）可以看出，如图2，定位误差主要集中在0 到1.5 米范围内。当L的值减小时，误差有明显的扩大。

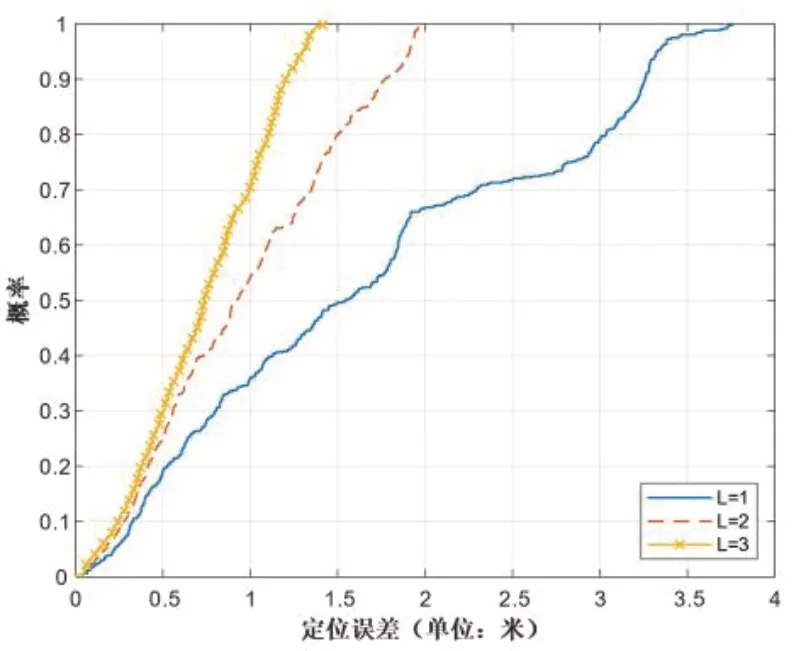
图2 不同L下的定位误差

此外，如图3 中姿态角误差的CDF 所示，当L等于3 米时，误差分布主要集中在-1 至1 度的范围内。尽管随着L的减小，这种分布无明显变化。以上数据说明，增大LED 之间的距离可以减小算法的定位误差，提升算法性能，但对姿态角误差无明显影响。

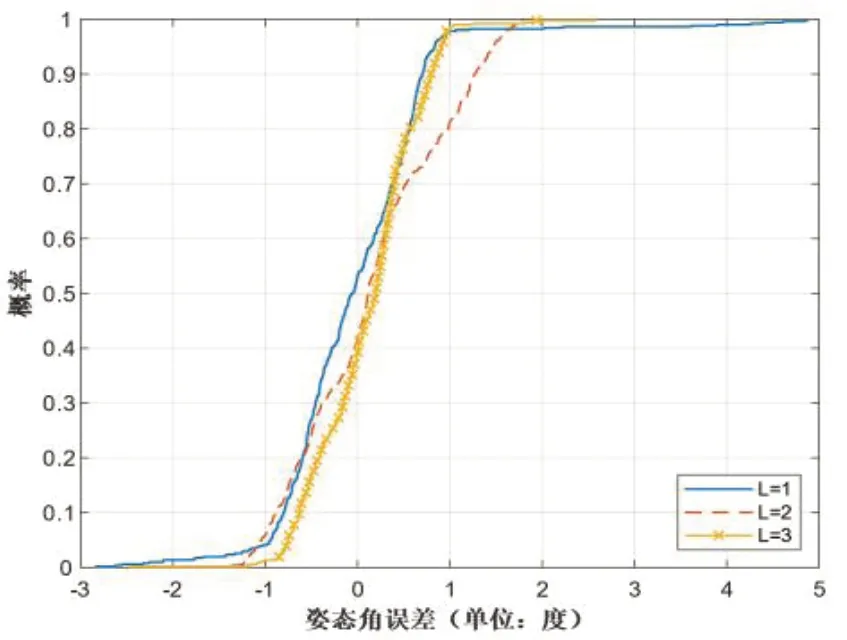
图3 不同L下的姿态角误差

其次，设定L为3 m，改变标准差(σ)来评估图像噪声对算法性能的影响。同时，将本文的算法（Mono+UKF Pro）与之前的算法[13]（Mono+UKF）比较。如图4 和图5 所示，Mono+UKF Pro 的CDF 表明，越大的σ会导致定位误差和姿态角误差越大；并且与Mono+UKF 相比，Mono+UKF Pro 的角度误差和位置误差有明显的降低，说明了该算法性能的提升。然而，尽管增大σ会导致定位误差和姿态角误差的增加，但相对噪声等级σ的增加并未明显加剧这两种误差。这表明了该算法具有出色的鲁棒性，能够相对稳定地应对噪声等级的变化。

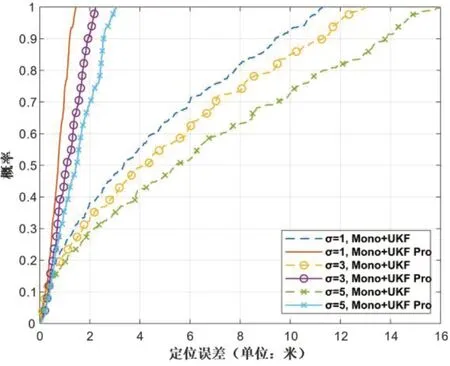
图4 不同σ下的定位误差

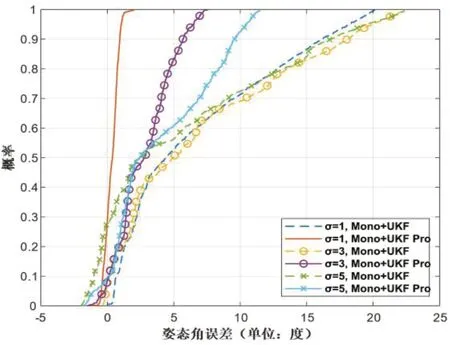
图5 不同σ下的姿态角误差

3 结束语

本文提出了一种基于VLP 的车辆位姿跟踪算法，专注于封闭环境下的定位应用。通过详细的仿真实验，验证了该算法在定位误差和姿态角误差方面的出色性能，而且即使在距离光源较远的情况下（120 m），算法仍能保持优异的表现。

值得注意的是，所提出的算法对高斯噪声表现出强大的鲁棒性。尤其在姿态角误差方面，该算法的鲁棒性尤为显著，即使图像噪声水平逐渐增加，也未对性能产生根本性的不良影响。

所提出的算法不仅在位姿跟踪性能和鲁棒性方面表现出色，还在受到图像噪声干扰和大尺度距离范围的河流流量测量中展现了其潜力。更为重要的是，该算法的应用领域不仅仅局限于车辆位姿测量，还适用于GNSS 信号不可用的环境，可扩展到机器人导航、工业规划等类似场景。

然而，该算法也存在局限性，特别是在LED 点移动超出图像边界时性能受到严重影响的问题。未来的工作将重点解决这一挑战，并探索将该算法融入到全局位姿跟踪技术中，例如将其整合到SLAM（同步定位与地图构建）中，以提升适用范围和性能。