一种高精度轨道单元及其在车辆-轨道耦合系统的应用

刘林芽，崔巍涛，秦佳良，左志远

(华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013)

随着列车运行速度的提升、行车密度的提高以及新型车辆和轨道结构形式大量投入工程应用,导致轮轨相互作用更加复杂,甚至会影响列车的安全运行[1-3]。进行车辆-轨道系统动力学分析是研究复杂轮轨关系和相互作用机制的基础[4],是优化车辆、轨道结构设计必不可少的内容。

针对轨道结构的建模方面,国内外学者开展了大量的研究[5-7]。Clark等[8]建立考虑钢轨弹性点支承和轨枕的振动的有砟轨道结构模型,分析了钢轨波磨对轮对与轨道结构振动的影响。Nielsen等[9]建立包含转向架、轮对、下部轨道基础为一体的有限元模型,采用复模态叠加法分析了车轮扁平、钢轨磨耗等因素对轨道结构振动影响的影响。雷晓燕[10]基于有限元理论建立了车轮-有砟轨道动力计算模型,分析高速列车对不同道砟厚度的动力响应。随着高速铁路的发展,无砟轨道由于整体性好和养护维修工作量少等优点得到了广泛应用。Guigou-Carter等[11]提出一种二维的板式轨道预测模型,扣件的阻尼建模为滞后阻尼且采用复刚度进行考虑,分析了扣件的动刚度变化对下部轨道结构减振性能的影响规律。Khajehdezfuly等[12]建立二维的车辆-板式无砟轨道有限元分析模型,钢轨采用Timoshenko梁模拟,扣件采用点支承的弹簧阻尼单元模拟,研究了扣件刚度变化对轮轨相互作用的影响规律。翟婉明等[13]基于模态叠加法建立一种车辆-板式轨道相互作用模型,钢轨视为连续弹性点支承基础上的欧拉梁,研究了砂浆层阻尼或刚度改变对系统振动的影响规律。蔡成标[14]建立列车-轨道-基础耦合分析模型,将钢轨视为弹性点支承的欧拉梁,轨道板和底座板视为弹性薄板,研究了板式轨道及过渡段的动力学性能。文献[15-16]基于弹性系统动力学总势能不变值原理,提出一种横向有限条与无砟轨道板段单元,比较了钢轨与轨道板的静、动态位移变化。Lei等[17]提出一种新型板式轨道单元,建立车辆-板式轨道-路基耦合动力学模型,评估了列车速度和轨道刚度对轨道振动的影响。上述研究对于轨道结构中扣件的模拟多采用点支承的弹簧阻尼单元模拟而忽略扣件垫板的支承长度。

另有一些学者采用仿真软件建立精细化轨道模型进行研究。Ganesh等[18]建立有砟轨道结构有限元模型,扣件垫板采用solid92单元模拟,分析谐响应激励下扣件、道砟和路基参数变化对轨道结构的影响。Oregui等[19]提出一种轨道有限元模型,钢轨和轨枕采用实体单元,扣件采用多个弹簧-阻尼单元组成的面区域模拟,研究了锤击试验下轨道结构的振动特性以及扣件胶垫建模形式对轨道动力学的影响。Zhao等[20]采用有限元法建立科隆蛋扣件系统的轨道真实有限元频域分析模型,利用该模型进行了数值模拟和轮轨振动特性分析。上述模型建立往往需借助仿真软件,单元数量多,计算效率不高。

本文建立一种更精确的轨道单元模型,模型中考虑扣件胶垫的支承长度和钢轨的剪切变形,可以得到更准确的高频振动响应。为便于计算程序的设计,减小总刚度矩阵的带宽,取两扣件之间的一跨钢轨、轨道板、底座板作为一个单元,钢轨视为扣件分布支承的Timoshenko梁,轨道板和底座板视为连续支承的Euler梁,轨道结构采用黏弹性弹簧-阻尼单元连接。车辆和轨道通过非线性轮轨接触关系耦合在一起,采用显-隐式积分法求解耦合系统的动力响应,并验证算法的正确性,然后比较扣件集中支承和分布支承下车辆、轨道结构的动力响应及轮轨相互作用,最后研究不同扣件胶垫支承长度对车辆、轨道结构振动的影响。

1 车辆-轨道耦合系统动力学模型

根据车辆-轨道耦合动力学理论,建立高速列车-板式轨道耦合系统模型,车辆为考虑一系和二系悬挂的整车模型,轨道为三层板式无砟轨道模型,其中采用分布式弹簧阻尼元件模拟扣件垫板的支承长度,建立更加精确的轨道单元模型,两个子系统通过非线性接触关系耦合,见图1。

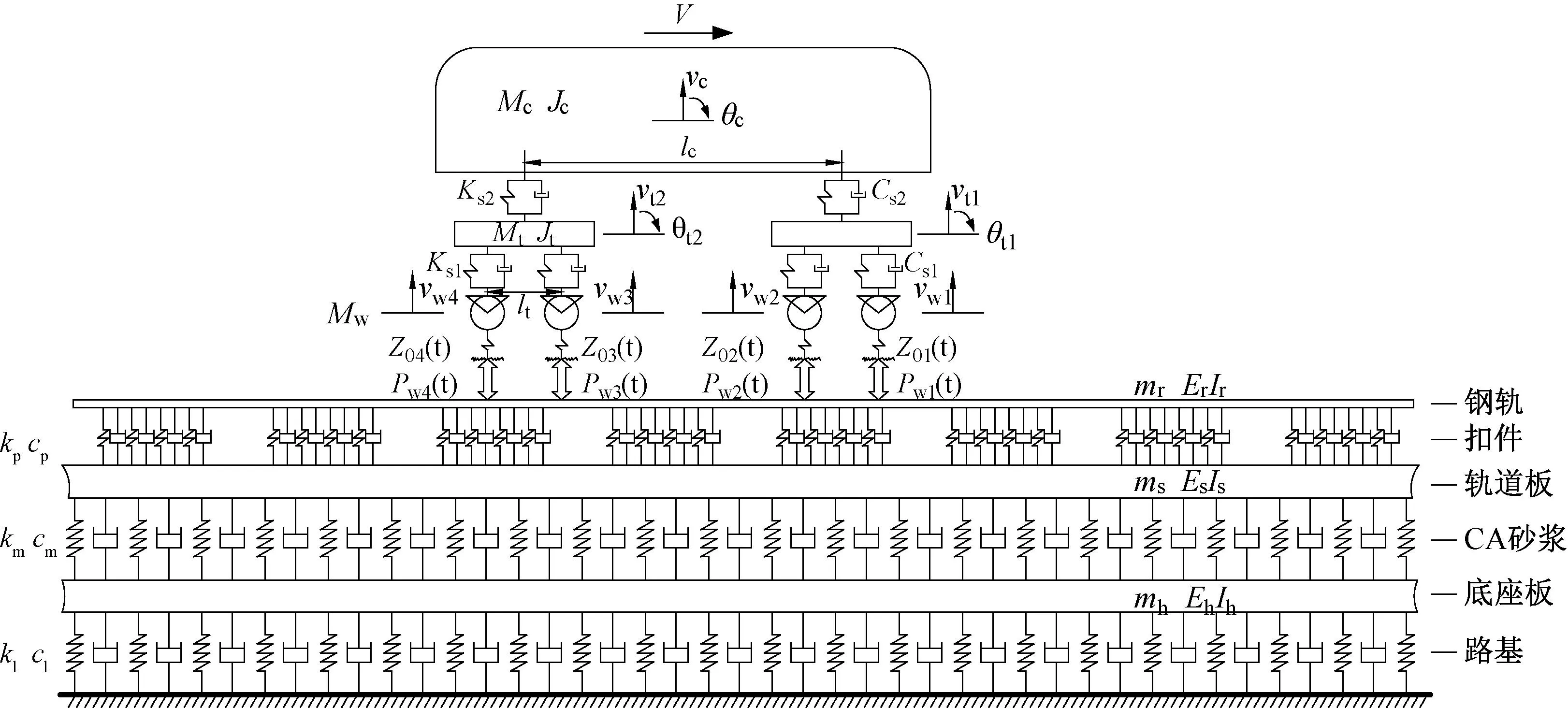
图1 车辆-轨道耦合系统模型

Mc和Jc分别为车体的质量和转动惯量;Mt和Jt分别为转向架的质量和转动惯量;Mw为轮对的质量;Ks1和Cs1分别为一系悬挂的刚度和阻尼;Ks2和Cs2分别为二系悬挂的刚度和阻尼;lc为车体上两转向架中心之间的长度;lt为转向架两轴之间的距离。Z0i(t)、Pwi(t)(i=1,2,3,4)分别为第i个车轮接触处的不平顺幅值和轮轨垂向力;ρr、Er、Ir分别为单位长度钢轨的质量、钢轨的弹性模量和绕水平轴的截面惯性矩;ρs、Es、Is分别为单位长度轨道板的质量、轨道板的弹性模量和绕水平轴的截面惯性矩;ρh、Eh、Ih分别为单位长度底座板的质量、底座板的弹性模量和绕水平轴的截面惯性矩。kp、cp分别为扣件的刚度和阻尼;km、cm分别为轨道板下沥青水泥砂浆层的刚度和阻尼;kl、cl分别为路基层的刚度和阻尼。

1.1 高精度的轨道单元模型

轨道子系统包括钢轨、扣件、预制轨道板、CA砂浆、底座板和路基,采用有限元法建立三层板式轨道单元模型[21]。当扣件考虑为集中支承时,板式轨道单元的长度l取钢轨两个相邻离散支承点之间的距离,轨道板和底座板的长度与钢轨一致,将钢轨、轨道板和底座板视为组合单元,见图2(a);当扣件考虑为连续支承时,仍取该长度作为板式轨道单元的长度,此时扣件考虑为连续支承的弹簧阻尼单元,长度lr为二分之一的扣件胶垫宽度,见图2(b)。

图2 三层板式轨道单元模型

两种板式轨道单元模型为12个自由度,v1、v4分别为钢轨的竖向位移;v2、v5分别为轨道板的竖向位移;v3、v6分别为底座板的竖向位移;θ1、θ4分别为钢轨的转角;θ2、θ5分别为轨道板的转角;θ3、θ6分别为底座板的转角。只需形成单元的质量、刚度和阻尼矩阵,便可方便地按有限元集成规律组集,得到任意长度的轨道系统的总质量、总刚度和总阻尼矩阵。单元内任何一点的位移可以通过插值函数N和单元节点位移ae表示,即

X=Nae

(1)

式中:

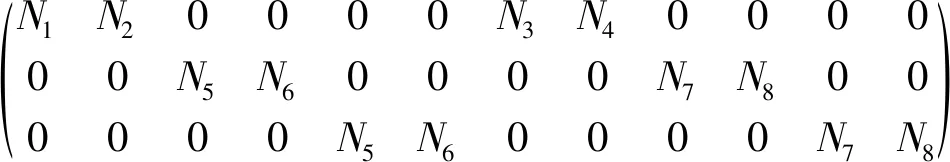
ae=

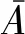
1.1.1 板式轨道单元质量矩阵

板式无砟轨道单元的质量矩阵为

(2)

(3)

式中:

(4)

式中:As为轨道板的截面面积。

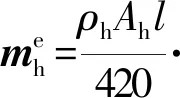
(5)

式中:Ah为底座板的截面面积。

1.1.2 板式轨道单元刚度矩阵

板式轨道单元的刚度矩阵为

(6)

(7)

(8)

(9)

单元中任意一点钢轨与轨道板之间的相对位移vrs为

vrs=vr-vs=N1v1+N2θ1+N3v4+N4θ4-N5v2+

N6θ2+N7v5+N8θ5=

(10)

故扣件胶垫层的弹性势能为

(11)

扣件分布支承引起的刚度为

(12)

(13)

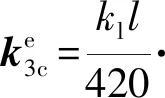
(14)

1.1.3 板式轨道单元阻尼矩阵

(15)

最后,按有限元集成规则组集单元质量、刚度和阻尼矩阵(式(2)、式(6)和式(15)),可得到三层板式轨道结构的总质量、总刚度和总阻尼矩阵分别为

(16)

运用Lagrange方程,可以得到板式轨道结构的有限元方程,写成统一的形式,即

(17)

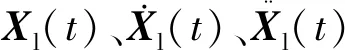
1.2 车辆单元模型

车辆子系统考虑一个车体、两个转向架的点头和沉浮及四个轮对的沉浮共10个自由度。定义车辆单元的位移向量为

(18)

式中:vc和θc分别为车体的竖向位移和角位移;vti和θti(i=1,2)分别为前、后转向架的竖向位移和角位移;vwi(i=1,2,3,4)为第i个轮对的竖向位移。

运用Lagrange方程,可得到车辆子系统的动力学方程为

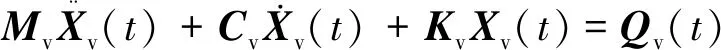
(19)

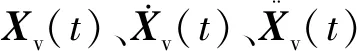
1.3 轮轨接触关系

采用Hertz非线性弹性接触理论,轮轨力为

(20)

式中:G为轮轨接触常数,m/N2/3;δZj(t)(j=1～4)为轮轨间的弹性压缩量,m。

轮轨间的弹性压缩量为

δZj(t)=vwj(t)-Zrj(t)-Z0j(t)

(21)

式中:vwj(t)、Zrj(t)分别为轮对和钢轨接触位置的垂向位移;Z0j(t)为轨道不平顺幅值。

2 数值求解及模型验证

2.1 显-隐式数值积分法

车辆和轨道两个子系统通过非线性轮轨接触力实现耦合,故需要采用数值积分进行求解,常用的数值积分方法有隐式法和显式法。显式法中,新型快速显式积分法[23]在质量矩阵为对角阵或经对角化,不需要联立求解高阶线性代数方程组,求解效率高且更经济。隐式法中,当考虑高频时要求极小的时间积分步长,隐式法每一步长都需要求解一次动力学方程,且对于非线性问题,需要采用交叉迭代控制精度范围内系统时程响应始终是收敛的,计算工作量大。

本文车辆系统因采用集中质量法建模,质量矩阵为对角阵,采用新型显式积分法求解;轨道模型采用有限元法建模,质量矩阵为协调质量矩阵非对角阵,故采用隐式Newmark数值积分法求解,即采用显式-隐式数值积分法求解车辆-轨道非线性耦合系统动力分析模型,避免了交叉迭代,提高了计算效率,同时具有较好的结果。采用Matlab编制相应的程序,主要计算步骤如下:

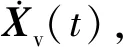
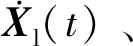
Step3根据轨道结构位移Xl(t)可得到轮轨接触处的钢轨位移Zrj(t),由式(20)计算轮轨力Pwj(t)。

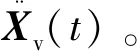
需注意的是,在起步时,先假设轨道结构初始位移Xl(0)(一般取Xl(0)=0)。同时,显式积分法令φ=ψ=0,具有积分“自开始”的特性。

2.2 模型验证

采用文献[24]中相同的条件对模型和求解方法进行验证。车辆模型为日本新干线300系列高速列车,轨道为三层板式无砟轨道,轨道不平顺选用钢轨接头焊缝不平顺。钢轨焊缝不平顺满足

(22)

式中:a1和L1分别为长波的波深和波长;a2和L2分别为短波的波深和波长。

当车辆以250 km/h的速度通过焊接区时,长波的波深和波长分别为0.3 mm和1 m,短波的波深和波长为0.2 mm和0.1 m。采用显-隐式积分法求解板式轨道的动态响应,积分步长为0.000 1 s。显隐式积分法计算结果见图3。并与文献[24]中的结果进行对比,见图4。由图4可知,本文所提出的模型计算结果与文献的结果吻合较好,表明本文建立模型的正确性。文献[24]中积分步长为0.000 02 s,本文采用较小的积分步长仍得到较好的计算结果,提高了计算效率。

图3 显隐式积分法计算结果

图4 文献[24]的计算结果

3 扣件分布支承式轨道模型下车辆-轨道耦合系统动力响应分析

3.1 计算参数

在仿真分析中,车辆选用中国CRH3高速客车,运行速度为300 km/h,轨道采用CRTS Ⅱ型无砟轨道结构,具体参数见表1。

表1 车辆与轨道具体参数

3.2 扣件支承形式对耦合系统动力响应影响

轨道不平顺选择我国高速铁路无砟轨道不平顺谱,波长范围为2～200 m,同时将其延伸至波长0.1 m作为短波不平顺激励[25]。应用上述的模型和计算参数,研究采用不同扣件支承形式下车辆-轨道耦合系统的动力响应,其中FCS为扣件集中支承,FDS为扣件分布支承,见图5。图5(e)、图5(h)中钢轨的动力响应取在轨道结构跨中位置。

如图5(a)～图5(e)所示,在时域内,与FCS模型相比,FDS模型的轮轨力、轮对加速度和钢轨加速度峰值均减小,波动范围变窄,FCS模型的轮轨力、轮对和钢轨加速度最大值分别为98.291 kN、21.419 m/s2、247.184 m/s2,FDS模型的轮轨力、轮对和钢轨加速度最大值分别为97.705 kN、20.681 m/s2、239.874 m/s2,差异约为0.6%、4.231%和3.047%。在频域内,两种模型的轮轨力在70～140 Hz以及1 000 Hz附近存在较小差异,FDS模型的振幅通常小于DCS模型振幅。轮对和钢轨加速度采用1/3倍频加速度振级可以明显看出,两种模型在125、1 000 Hz频段存在区别,FCS模型大于FDS模型的计算结果。第一主频在63 Hz,由车辆与轨道共同弹性变形的耦合共振引起。第二主频为1 000 Hz附近,由钢轨的垂向“pinned-pinned”振动引起。考虑胶垫支承长度的FDS模型在1 000 Hz频段加速度振级更小,与文献[26]规律一致,更精确地反映了两个模型之间的差异。从图5(g)～图5(h)可以看出,对于轮对位移和跨中钢轨位移,与FCS模型相比,FDS模型的轮对和钢轨的位移均较小,但差异均小于0.5%。

3.3 扣件胶垫支承长度对车辆-轨道耦合系统的影响分析

在FDS模型的基础上,进一步研究扣件系统中胶垫支承长度对车辆-轨道耦合系统垂向动态响应的影响,橡胶垫板的支承长度设置为50、150、250 mm,计算结果见图6。为了更直观地反映胶垫不同支承长度的区别,不考虑外部激励作用,并假设钢轨表面平顺。另外,图6(a)、图6(b)响应参照系取在车辆上,图6(c)～图6(h)钢轨、轨道板和底座板的响应参照系取在地面上。

图6 扣件胶垫支承长度对轨道结构的影响

如图6(a)、图6(b)所示,由于弹性胶垫的周期性支承,轮轨力和轮轨接触处的轮对位移呈现周期性变化,变化幅值随着胶垫支承长度的增加而减小。当扣件胶垫长度分别取50、150、250 mm时,最大轮轨力分别为71.278、71.205、71.167 kN;最大轮对位移分别为1.005 38、1.004 89、1.004 51 mm。随着胶垫支承长度从50 mm增加到250 mm,最大轮轨力和轮对位移减小了0.15%和0.08%。图6(c)～图6(e)反映了随胶垫支承长度变化,钢轨、轨道板和底座板加速度的变化,随着胶垫长度的增加,钢轨、轨道板和底座板的加速度均减小,其中胶垫支承长度的变化对钢轨影响最大。当扣件胶垫长度取50 mm,钢轨、轨道板和底座板加速度最大值分别为15.151、0.736、0.598 m/s2;扣件胶垫长度取250 mm,钢轨、轨道板和底座板加速度最大值分别为14.627、0.718、0.577 m/s2,分别减小3.582%、2.506%和3.639%。图6(f)～图6(h)反映了胶垫支承长度变化钢轨、轨道板和底座板位移的变化,随着胶垫长度的不断增加,钢轨、轨道板和底座板的位移也均略有减小,但影响较小。随着支撑长度从50 mm增加到250 mm,钢轨、轨道板和底座板的最大位移分别减小了0.6%、0.2%和0.08%。

4 结论

本文基于车辆-轨道耦合动力学理论,采用有限元法建立了更精确的考虑扣件胶垫的支承长度和钢轨的剪切变形的轨道单元模型,将其应用于车辆-轨道耦合系统动力学,采用显-隐式积分法求解耦合系统动力学响应。研究了扣件模型支承形式和长度对车-轨耦合动力学的影响,得到以下结论:

1)该轨道单元模型考虑了钢轨的剪切变形及扣件的分布支承,具有精度高、编程简捷清晰的优点。

2)扣件考虑集中支承时会高估轮轨相互作用以及轮对和钢轨的振动,采用扣件分布支承式轨道单元模型可以更精确地预测“pined-pined”频率范围附近的轮轨相互作用。

3)扣件胶垫支承长度的增加可以降低轮轨相互作用,实际工程中可以适当增加扣件胶垫的支承长度来减小轨道结构的振动。

4)采用本文建立的车辆-轨道耦合模型及显-隐式积分算法可以在降低计算成本的情况下给出更为准确的轨道结构振动响应。