基于状态空间模型的结构外部激励计算与响应重构

彭珍瑞，史鹏程

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

近年来随着我国综合国力的提高,建造了大量铁路桥梁、隧道等大型土木工程。对于这些大型土木工程结构进行实时的健康监测是很有必要的,但是这类土木结构的服役时间远长于对其进行监测的传感器寿命,若部分传感器老化失效,则对应的响应信息则会丢失。同时,传感器布置的位置和数量往往受到经济原因、传感器安装条件等方面的限制,监测结构所有节点上的响应是较为困难的。因此,研究一种使用少量响应来重构所需响应及激励的响应重构技术就显得十分重要[1-4]。

当前的响应重构方法有以下三类:第一类通过传递率进行重构[5-7],此方法通过建立未知响应和已知响应的传递关系来重构未知响应,这需以精准的有限元模型为基础,且无法消除传感器测量噪声对计算结果的影响。第二类为基于大数据分析的结构响应重构方法[8-9],此方法使用深度学习、宽度学习等机器学习方法,分析学习已有监测数据与所需重构数据之间的隐性关系,实现对未知信号的重构。但此类方法需要大量数据进行分析、学习,且目前的研究仍处于起步阶段。第三类以状态空间模型为基础,使用卡尔曼滤波类(Kalman filter,KF)算法进行重构。张笑华等[10]率先使用KF算法进行响应重构和传感器优化布置。Xu等[11]以悬索桥为试验对象,使用此方法完成了多类型响应信息的重构。Hu等[12]采用KF算法对一高层建筑的各类响应进行重构,并将重构后的数据用于地震前后结构性能评估和安全预警。Zhang等[13]将大型复杂结构分为若干个子结构后基于KF算法进行结构响应重构,并将重构的响应应用于结构损伤识别。

上述方法都需要事先测得结构外部激励,但在工程实际中结构外部激励信息往往较难获得。在结构动力学分析、模型修正以及健康监测等领域,外部激励信息尤为重要。因此,若能在外部激励未知的情况下,实现对结构外部激励和各处响应的重构将具有非常重要的意义。Liu等[14]基于状态空间模型推导了外部激励与结构响应的传递矩阵,并结合正则化方法优化传递矩阵,用于重构外部激励和结构响应。董康立等[15]基于类卡尔曼滤波算法实现对结构外部激励和响应进行重构。

此外,由于工程测量中的噪声大部分是有色噪声而非白噪声,而使用KF算法必须满足噪声为白噪声,若忽略此差异则定会影响重构结果。粒子滤波算法是继KF类算法后发展的一种可处理有色噪声的滤波算法,近期不少学者成功将智能优化算法和粒子滤波算法相结合,以改善粒子贫化现象[16-17]。

因此,针对上述问题,本文从外部激励计算结合多类型响应重构的角度出发,首先基于状态空间模型推导出结构外部激励计算公式。然后,将外部激励和结构模态坐标组合成新的状态向量,构建增秩状态空间模型,并引入改进的粒子滤波算法,处理测量数据中的有色噪声,完成使用部分测量加速度响应对结构其余位置速度、加速度响应的重构和外部激励的计算。最后对钢轨和外伸梁分别进行数值模拟和试验分析,验证本文方法的有效性。

1 状态空间模型及外部激励计算

1.1 二阶运动方程的状态空间模型

结构的二阶运动方程在模态空间中可表示为

(1)

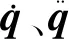
由以上二阶运动方程建立状态空间模型,即

xk+1=Axk+Buk

(2)

yk=Cxk+Duk

(3)

式中:xk、yk、uk分别为离散后的状态向量,观测向量以及外部激励向量;A和B分别为状态矩阵和输入矩阵;C和D分别为输出矩阵和直接传输矩阵。若观测量为结构各节点的加速度,则式(2)和式(3)中的各项具体表示为

(4)

(5)

(6)

(7)

D=ΦΦTL

(8)

1.2 状态空间模型下的激励计算

由状态空间模型可推导出各时刻的结构的外部激励向量uk。

由式(2)可得

xk=Axk-1+Buk-1

(9)

将式(9)代入式(3)可得

yk=C(Axk-1+Buk-1)+Duk

(10)

由式(10)可建立观测量yk与外部激励向量uk的关系为

uk=(DTD)-1DT(yk-C[Axk-1+Buk-1])

(11)

通过式(11)可由结构各处测得的各类响应计算出结构外部激励,但由于工程测量中往往存在一定的噪声影响,直接用式(11)计算得出的结果必然与实际存在一定的差距。为了减小测量噪声带来的影响,将建立结构状态向量xk与外部激励向量uk的联合增秩状态向量,并进行滤波处理。

1.3 增秩状态空间模型

由式(11)计算外部激励向量后,外部激励向量在k时刻至k+1时刻的增量Δuk为

Δuk=uk+1-uk

(12)

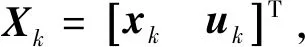
Xk+1=AaXk+BaΔuk+wk

(13)

Yk=CaXk+vk

(14)

式中:wk和vk分别为系统噪声和测量噪声;若重构响应为速度和加速度响应,则其余各项具体表示为

(15)

(16)

(17)

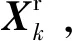
(18)

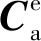
2 结合萤火虫算法的粒子滤波算法

2.1 粒子滤波算法

由于测量噪声的影响,若直接使用上述方法进行未知响应和外部激励的计算,其结果必然不准确。且实际工程中的噪声多为有色噪声,因此引入改进的粒子滤波算法,以减小有色噪声对重构的响应和激励精度的影响。

基于第1节内容,系统状态空间模型可表示为

Xk=f(Xk-1,vk-1)

(19)

Yk=h(Xk,wk)

(20)

式中:Xk为状态向量;vk-1为系统噪声;Yk为观测向量;wk为测量噪声。

在传统的粒子滤波中,随着粒子集的不断迭代,会造成粒子退化,导致大量的算力浪费在极小权值粒子上。对此,Gordon等[18]提出重采样理论,但是重采样会降低粒子的多样性,从而引起粒子贫化。

2.2 萤火虫算法

萤火虫算法借用萤火虫个体移动的仿生思想实现寻优。萤光亮度IF为

IF=I0e-γd

(21)

式中:I0为初始亮度;γ为吸收系数;d为个体之间的距离。

个体之间的吸引度β为

β=β0e-γd2

(22)

式中:β0为初始吸引度。

位置变化表示为

(23)

式中:Xi和Xj分别为两个体i和j的位置,i和j分别为两个粒子;α为步长因子;E为n×1的全一矩阵;rand为随机数。

2.3 结合萤火虫算法的粒子滤波

传统算法为了避免算法陷入局部最优,在式(23)中添加了随机项,但式(13)中各行非同一个数量级,不可按原方法直接运算,改进运动更新,即

(24)

(25)

2.4 算法步骤

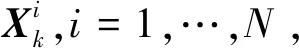
(26)

式中:q为粒子的重要性分布。

Step2将萤火虫算法中的萤火虫个体看作粒子滤波中的粒子,根据式(22)及式(24)计算粒子i的吸引度并指导其进行移动。

Step3根据式(25)的荧光度值更新最优粒子。

Step4当迭代次数达到预设值则停止迭代(本文中为15次)。

Step5计算并归一化粒子权重,计算状态向量并求得所需响应。

2.5 算法总结

引入结合萤火虫算法的粒子滤波算法处理测量响应中的有色噪声,优化粒子贫化问题,并对结合萤火虫算法的粒子滤波[18]进行适用性改进。结合1.3节中建立的增秩状态空间模型,可以在结构外部激励未知的情况下对结构进行响应重构并对外部激励进行计算,即通过部分测量加速度响应计算结构其余位置的未知速度、加速度响应和外部激励。

3 数值模拟

采用一根60 kg/m的钢轨模拟整个响应重构过程,该钢轨长度为600 mm,弹性模量、密度和泊松比分别为200 GPa、7 850 kg/m3和0.3,在钢轨两端的底部两侧施加约束,模拟扣件对钢轨的固定。进行响应重构时,以前5阶模态振型为目标模态,对应的固有频率分别为286.94、637.38、1 071.71、1 117.31、1 644.42 Hz。如图1所示,钢轨从左到右划分为20个单元,从左到右节点编号分别为1～21,其中1和21节点受到约束。在钢轨上端的第16节点施加垂向锤击激励,现通过测量钢轨上端的7节点、19节点的垂向加速度响应来重构10节点和16节点的垂向速度和加速度响应,并计算外部激励。为了模拟正常工作的传感器的测量响应,在测量响应中加入3%的有色噪声,有色噪声的功率谱见图2。提取所需重构点的测量响应与重构响应进行对比,见图3。

图1 测点布置

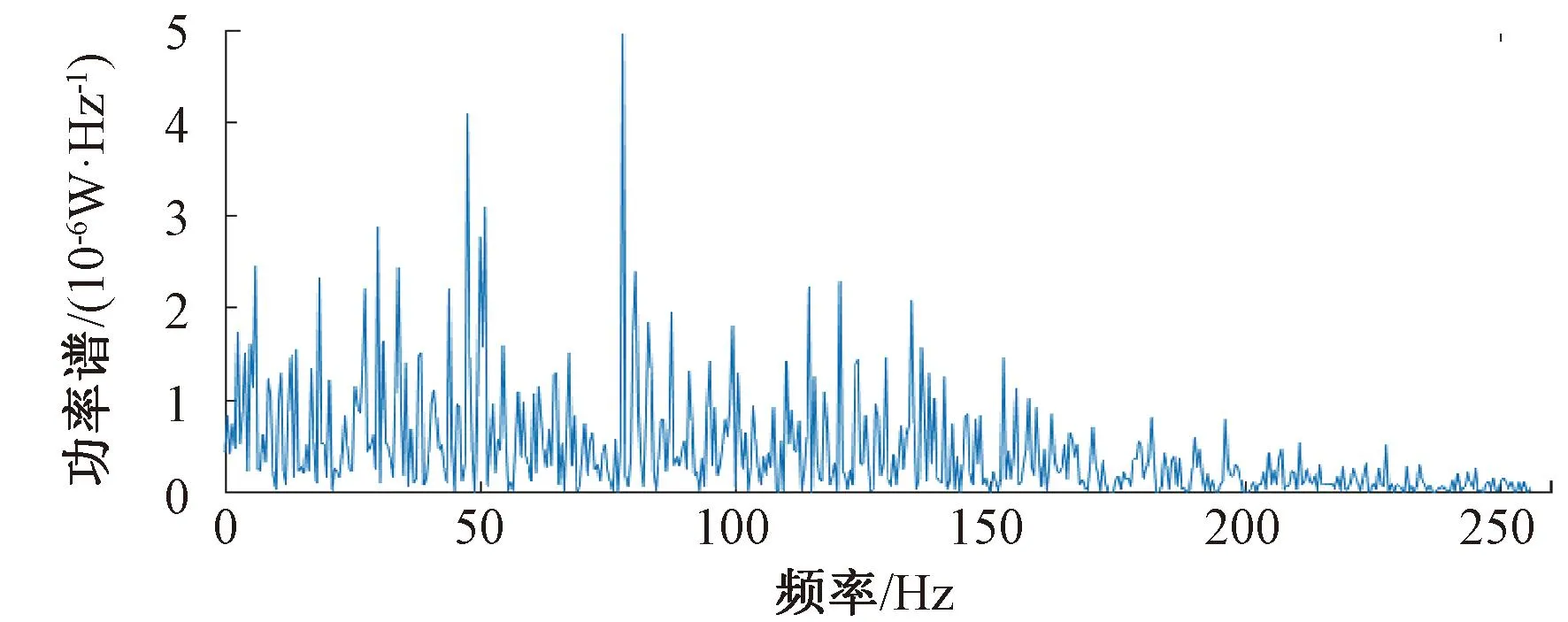
图2 有色噪声功率谱

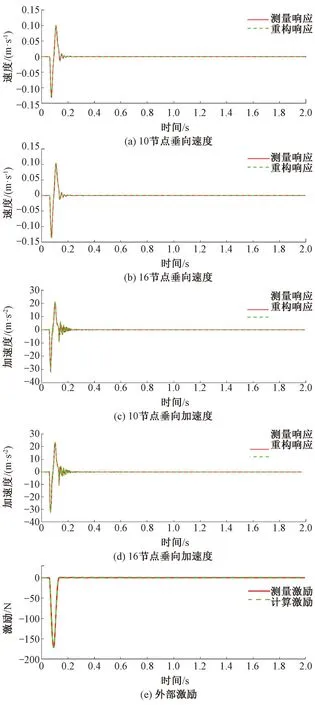
图3 重构信息与测量信息对比

由图3可知,所提方法在3%的有色噪声下,能够对结构的未知响应进行有效重构,并能计算出结构外部激励。同时,粒子质量可以通过粒子的权重间接反映。某一时刻的粒子权重见图4,由图4可知,权重分布良好,没有发生粒子退化或粒子贫化现象。

图4 粒子权重

为探究此方法在不同等级的噪声条件下的重构效果,分别在测量响应中加入6%和10%的噪声,使用相对百分比误差eRPE来衡量重构精度,具体公式为

(27)

式中:std为标准差函数;Ye为由式(18)重构得出的响应;Yr为提取的真实响应。

计算得到的相对百分比误差见表1。由表1可知,在不同等级的噪声下,重构出的各点响应以及激励的精度随着噪声的增强,精度逐步降低。重构的响应和外部激励在各等级噪声的影响下,相对百分比误差均低于5%。综上分析,所提方法在不同的噪声条件下能对结构各点未知响应进行有效重构,并能计算出结构外部激励。测量噪声对重构精度有一定的影响,但总体精度仍保持较好水平。

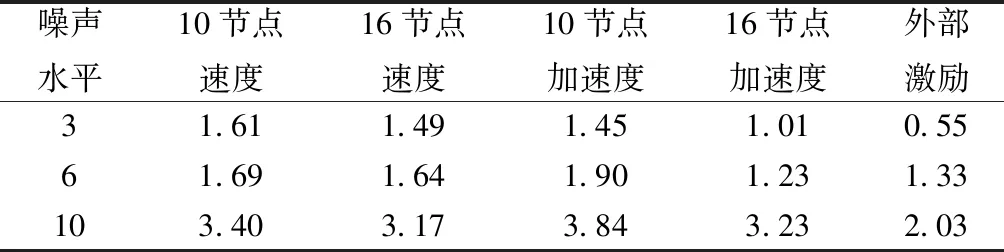
表1 相对百分比误差 %

为了探究在不同形式的外部激励下此方法的稳定性,将施加激励由锤击激励变为正弦激励,得

us=20sin(5πt)+50sin(15πt)+20sin(60πt)

(28)

激励施加位置仍然为16节点,方向为垂直向下。所加噪声仍为3%的有色噪声,测量响应为7节点、19节点的垂向加速度响应,所需重构响应为10节点和16节点的垂向速度和加速度响应。重构效果见图5。

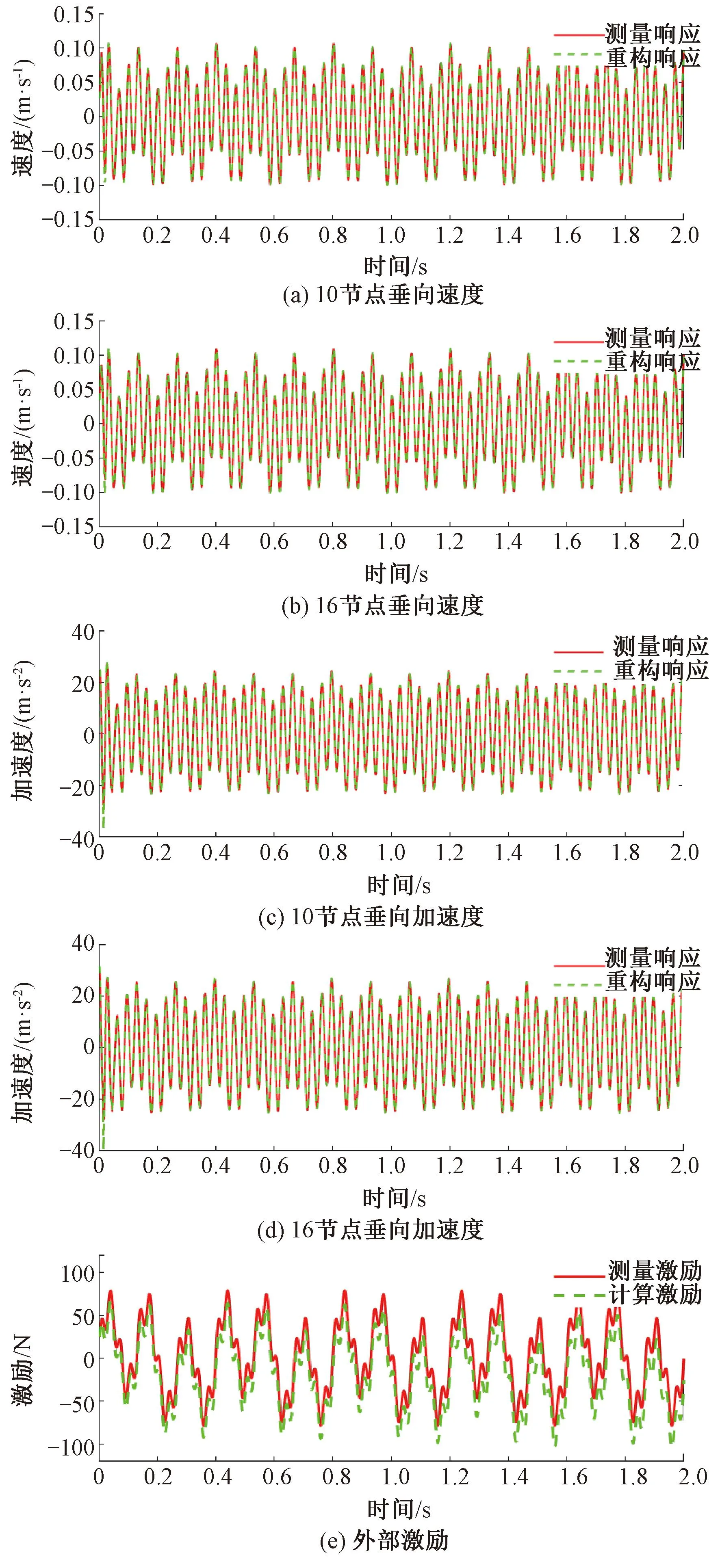
图5 正弦激励下重构信息与测量信息对比

由图5可知:在正弦激励下,结构响应以及外部激励仍然能被有效地重构,10节点垂向速度、16节点垂向速度的RPE分别为2.99%、2.97%;10节点垂向加速度、16节点垂向加速度的RPE分别为3.70%、3.99%;外部激励重构的RPE为4.14%。不同的激励下的重构精度略有改变,但总体精度仍然保持良好,验证了此方法适用于不同类型的外部激励。

4 试验验证

为进一步验证所提方法在实际工程中的实用性,使用一根外伸梁作为试验对象,见图6。外伸梁尺寸为2 000 mm×100 mm×10 mm,外伸梁分为20个单元,21个节点,在第2和20节点施加约束。取前4阶模态振型进行响应重构,频率分别为11.53、35.42、69.70、118.99 Hz。如图7所示,在节点9的垂向施加锤击激励,在第8、11、14节点布置3个加速度传感器采集加速度响应,用于重构信号和外部激励的计算,同时在第5和17节点布置两个加速度传感器测量振动信号与重构值做对比。试验所采用的加速度传感器型号为ICP型的INV9821;网络分布式采集仪为北京东方振动和噪声技术研究所的INV3062-C2。

图6 外伸梁试验

图7 测点布置

重构响应与测量响应的对比见图8。由图8可知,重构响应与传感器测量响应吻合良好。5节点垂向加速度、17节点垂向加速度重构的RPE分别为18.19%、14.52%;5节点垂向速度、17节点垂向速度重构的RPE分别为16.34%、12.94%;外部激励重构的RPE为27.20%。由于所对比数据为传感器实测所得,存在一定的测量噪声,与实际响应稍有差距,试验中计算所得RPE与仿真算例相比必然有所增加。

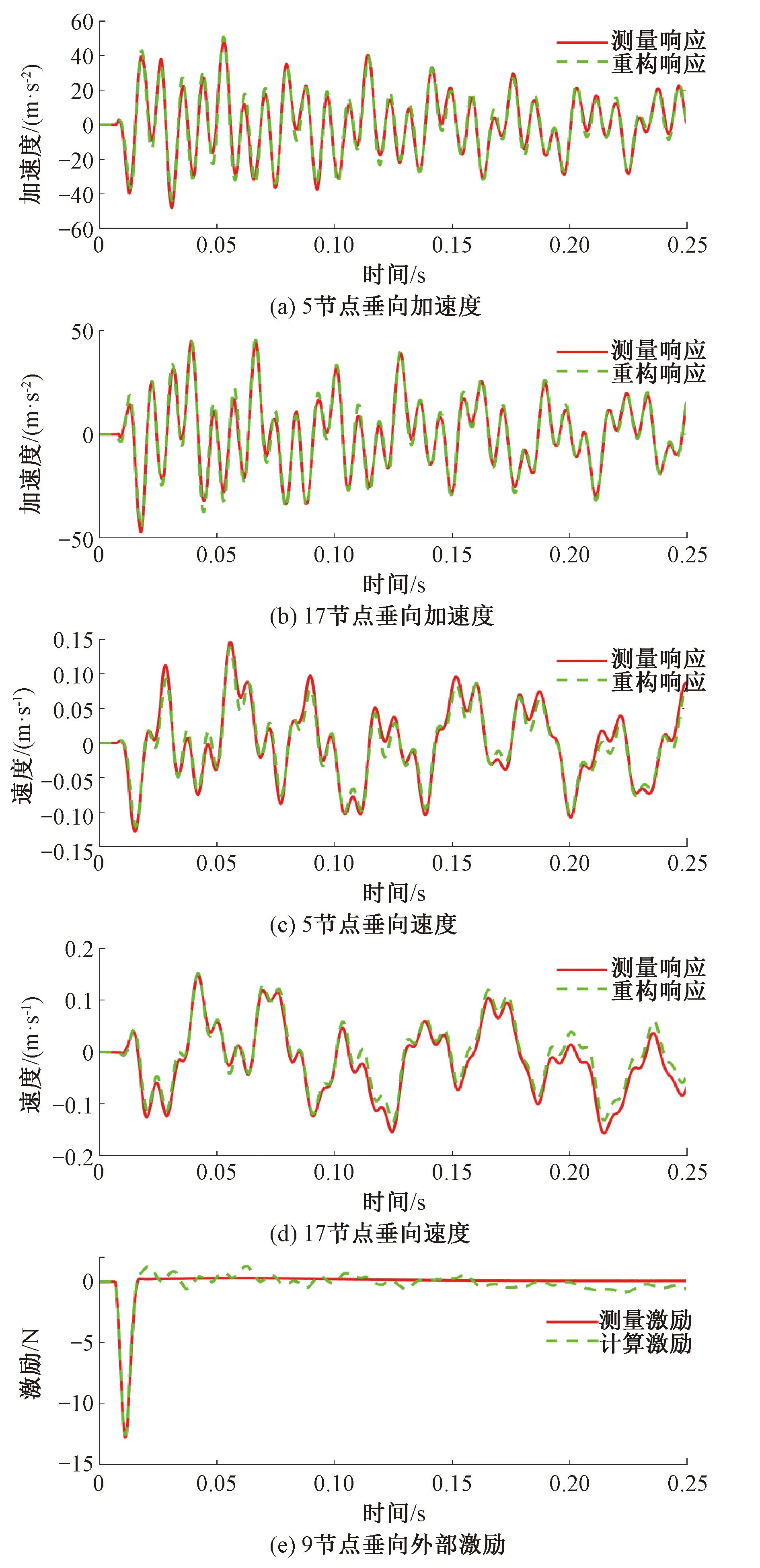
图8 重构信息与测量信息对比

综上所述,试验验证了所提方法能在使用少量加速度传感器所测得的结构振动加速度响应,实现对于结构其余未测量位置的速度和加速度响应的重构,并可以有效计算结构外部激励。

5 结论

本文研究了使用少量包含有色噪声的加速度响应,对结构其余各点的速度、加速度以及外部激励进行重构的方法,并分别进行了数值模拟和试验验证。结论如下:

1)提出的基于状态空间模型的结构外部激励计算与响应重构方法可在仅使用少量加速度响应的情况下对于结构其余位置的速度、加速度响应以及结构外部激励进行有效重构。

2)激励类型的改变以及噪声等级的变化未对重构的响应以及外部激励的精度造成较大影响,此方法可以适用于不同类型的激励,也具有一定的抗噪性。

3)外伸梁试验表明,该方法能够实现基于有限传感器的测量信息对结构其余各处响应及外部激励的重构,可以为后续的结构健康监测、损伤识别等提供更完备的响应数据。