考虑竖向地温应力的热力耦合瞬态岩爆预测研究

李天胜，何 川，周子寒，陈子全，包烨明，汪 波

(1.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2.中铁十二局集团有限公司，山西 太原 030024)

四川省西部地区隧道赋存的地质环境普遍存在高地应力、高地温的特点[1]。在温度应力的叠加效应下,隧道开挖后的环向应力将会显著增大,岩爆烈度随之增强[2-3]。然而,在以往设计阶段的岩爆预测模型中,作为应力边界条件来源的岩体初始地应力场反演结果由于未考虑竖向温度应力的影响,存在隧道岩爆烈度预测偏低的情况。鉴于此,研究高地温、高地应力环境下考虑竖向温度应力的岩爆瞬态预测方法对指导类似隧道工程的修建具有重要意义。

基于隧址区地勘及地应力实测资料,采用反演手段可获取岩体初始地应力场。针对这一领域,国内外学者在以下方面开展了大量研究工作。汪波等[4]利用多元线性回归方法结合最小二乘寻优准则求解了隧址区岩体初始地应力场,该方法的特点是能够确定反演唯一解,且运算速率较快。蒙伟等[5]同样基于这一方法,进一步考虑侧压力系数对一次反演结果进行修正,提高了反演精度。另一方面,随着智能算法的兴起,其在地应力反演领域同样应用广泛。刘泉声等[6]采用支持向量回归优化算法,减小了实测地应力随机误差对地应力反演的影响。裴书锋等[7]利用进化神经网络-遗传算法,提出考虑还原白鹤滩水电站岩体应力型破坏特征以修正反演结果的方法。运用智能算法可以较好解决实测值与计算值之间的非线性拟合问题,但决定拟合效果的数据训练样本需求很大,因此计算效率较低。

根据反演结果,分析总结初始地应力场的分布特征对指导地下工程的修建意义重大。陈世杰等[8]讨论了金川地下厂房断层带内外局部地应力场的分布规律,认为靠近断层带应力量值增大,而断层内部应力减小。周子寒等[9]分析了花岗质侵入岩地层初始地应力的分布特征,发现接近侵入体前沿区域岩体应力场集中现象显著。Li等[10]通过分析地应力反演结果得出隧道穿越断层或背斜时,主应力量值会突然下降的结论。

高能地质环境下硬岩隧道往往会发生岩体瞬时破坏(岩爆)现象,国内外学者在岩爆预测方面进行了相关研究:严健等[11]通过反演隧址区高精度地应力场,对岩爆发生类型、破坏形态进行了机理性探索。Meng等[12]研究了高地温高地应力环境下的岩体初始应力场,认为高地温环境下岩体初始地应力更大,可能会加剧岩爆程度。严健等[13]根据地应力场反演结果,采用热力耦合模型计算了拉林铁路桑珠岭隧道的岩爆烈度,但其应力边界条件未考虑温度应力的影响。

综上所述,利用反演求解的隧址区初始地应力场作为岩爆模型的应力边界条件求解岩爆烈度是岩爆预测的常规手段。然而,在以往的研究中,由于地应力反演过程未考虑高地温环境下竖向地温梯度产生的温度应力,进而造成岩爆预测结果“失真”。另一方面,采用热力耦合本构计算岩爆烈度也仅考虑稳态结果,开挖瞬间的瞬态岩爆烈度还未见报道。本文以康定某隧道为依托,在水压致裂法的竖向应力分量中叠加地温热应力,结合多元线性回归法计算效率较高的特点,反演了隧址区初始地应力场。在此基础上,以反演结果作为岩爆预测模型的应力边界条件,考虑隧道洞壁与洞内环境的对流换热过程,采用热力耦合本构模型求解了岩爆段落的瞬态岩爆烈度。研究形成了适用于高地温高地应力隧道初始地应力反演到瞬态岩爆预测的方法。研究成果可指导类似隧道工程的设计和施工。

1 工程概况

1.1 地形地貌及地层岩性

康定某隧道位于四川盆地与青藏高原过渡的西南边缘。受岷江、大渡河等水系的强烈切割,地形高差大,沟壑密布,山岭纵横。隧址区地表高程3 460～4 730 m,为典型高原地貌。隧道进口位于康定市折多塘村西面山坡,出口位于瓦泽乡水桥村318国道附近,隧道全长约20.8 km,最大埋深约1 215 m,地层岩性主要分布有黑云母二长花岗岩、石英砂岩、板岩。

1.2 研究区域地应力特征

隧道处于松潘—甘孜褶皱带,SN向川滇构造带和NW向鲜水河构造带在区域内形成中国西南著名的Y字形构造格局,隧址区大地构造背景处于Y字形构造三岔口交接部位的NW侧。隧道纵断面见图1。由图1可以看出,强烈的地质构造作用下,隧址区共计12处断层,其中,折多塘断层位于隧道进口附近,影响范围为3～5 km,因而仅以实际岩性表示。隧址区现今主应力方向为NW-NWW向,隧道大致走向为NW向,主应力方向与隧道走向近乎平行。为探明隧址区地应力分布情况,在地勘阶段采用水压致裂法进行了地应力测量,共计钻孔5处,地应力实测结果见表1。

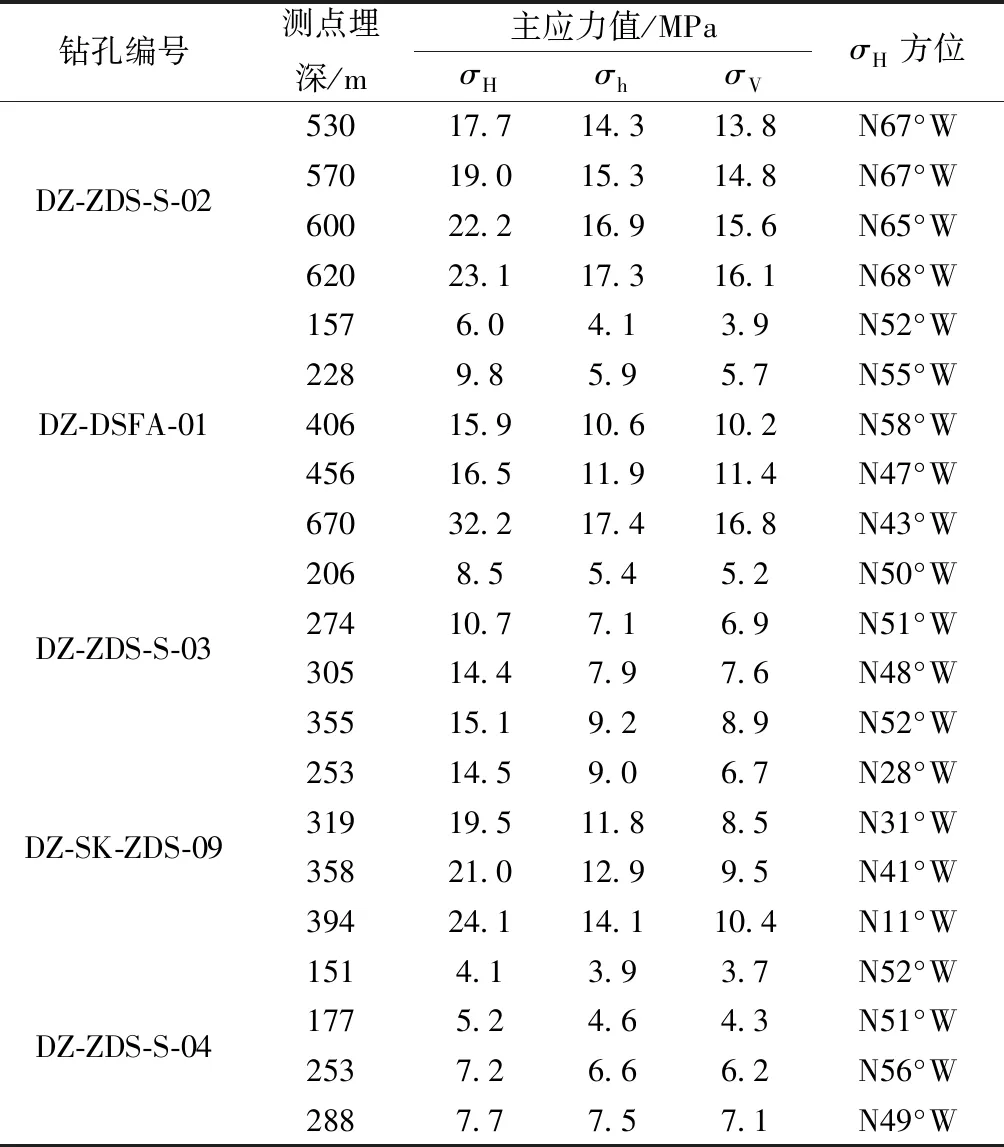
表1 水压致裂法地应力测量结果

图1 隧道纵断面

由表1可知,隧址区实测地应力中最大水平主应力σH、最小水平主应力σh和竖向应力σV的范围分别为4.1～32.2、3.9～17.4、3.7～16.8 MPa。受强烈的地质构造运动影响,隧址区初始地应力以水平向构造应力为主导,5处钻孔均呈现σH>σh>σV的分布特征。同时,实测地应力量值随着测点埋深的增大而增大。

最大水平主应力σH的方位角范围为N11°W～N68°W。其中,DZ-ZDS-S-02、DZ-DSFA-01、DZ-ZDS-S-03、DZ-SK-ZDS-09、DZ-ZDS-S-04钻孔σH的平均方位角分别为N67°W、N51°W、N50°W、N28°W、N52°W。地应力测量结果与大地构造走向基本一致。

1.3 隧址区高地温测量

隧道穿越玉龙希断裂有温泉出露,同时隧道进口穿越折多塘导热断裂,因此针对隧道赋存的高地温环境,在地勘阶段共计进行了3处测温钻孔测量地温梯度,见图2。

图2 隧道地温钻孔分布图

2 隧址区地应力反演原理

2.1 高地温环境水压致裂法测量原理

要探讨高地温环境下的地应力反演原理,首先需要分析大地温度梯度分布及水压致裂法的测量原理。地表往下不受大气温度影响的地层温度会随着深度的增加而增加,其增长幅度称为地温梯度,如图2中隧道的实测平均地温梯度为3.1 ℃/100 m。而岩体受到大地热流的影响将会发生热膨胀,在周围岩体的约束下产生热应力[14],即

σT=αβEZ

(1)

式中:σT为岩体在高地温环境下产生的热应力;α为地温梯度;β为岩体体膨胀系数;E为岩体弹性模量;Z=H-h,其中,H为埋深,h为变温带与恒温带高度之和,一般约为30 m。

假定高温膨胀无特定方向,则按式(1)产生的高温热应力呈静水压力的形式。

按照水压致裂法的原理[15],测点最大水平主应力σH和最小水平主应力σh的测量结果为初始地应力的真实结果,见图3,因此测量数据包含了热应力分量和构造应力分量

(2)

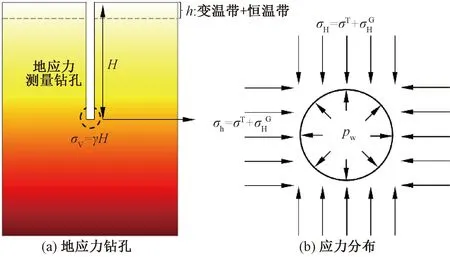
图3 高地温环境水压致裂法测量原理

(3)

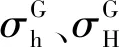
水压致裂法竖向应力却并非来自实际的测量结果,其是根据埋深对应的上覆荷载估计所得

σV=γH

(4)

显然竖向应力忽略了高地温环境下温度热应力分量,实际的竖向应力σ′V应为

σ′V=γH+σT

(5)

那么,以往在地应力反演过程中并未考虑竖向温度应力分量的影响,仅以σH、σh、σV作为实测值进行数据拟合反演显然是不妥的。

2.2 高地温环境地应力反演原理

首先将实测应力中包含温度应力的最大水平主应力与最小水平主应力剔除温度应力分量。以未含温度应力的水平应力参与地应力反演,则剔除温度应力后的两项水平主应力分别为

(6)

(7)

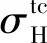
σv′w′=αv′vαw′wσvw

(8)

式中:σv′w′为三维数值模型坐标系的应力分量;σvw为实测应力坐标系的应力分量;v,w=x,y,z;αv′v和αw′w为坐标转化系数,如αv′w=cos(v′,w)。

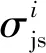
(9)

式中:b0为常数项;bi为第i种边界条件工况下的多元线性回归系数;n为工况总数。

利用统计学中最小二乘法原理,可以求解式(9)中的回归系数。假定有m个测点,每个测点有l个应力分量,则最小二乘法的残差平方和Qc为

(10)

式中:σkj为第k个测点的第j个应力分量实测值。

(11)

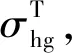
(12)

2.3 三维数值模型的建立

基于克里金插值法,提取地勘阶段获取的隧址区平面图三维坐标信息,导入ANSYS软件中建立三维数值模型的顶面。为避免计算结果受模型尺寸效应的影响,三维模型的高度方向尺寸应与宽度方向尺寸基本相当。鉴于平面图宽度方向的有效尺寸为4 000 m,因此,在高度方向上,三维模型的底面取至隧道进口高程以下2 000 m。模型长度方向包含隧道全部线路,约21 000 m。由于模型顶面及断层的不规则分布,对部分区域的网格划分进行加密处理。岩体材料的物理力学参数见表2。建立的三维数值模型见图4。

表2 岩体物理力学参数

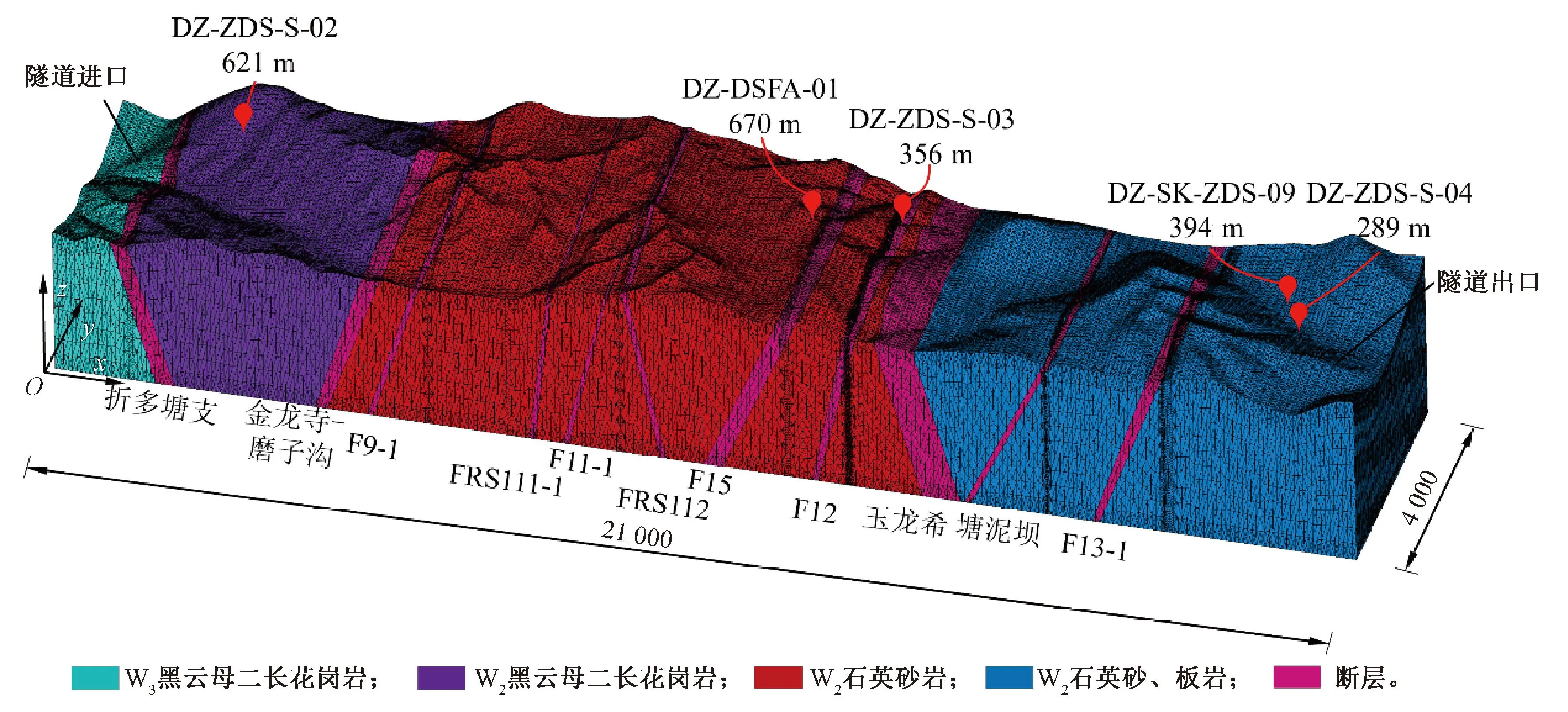
图4 三维数值模型(单位:m)

2.4 模型边界条件

考虑x、y方向的构造作用,xoy平面的剪切构造作用。对三维数值模型(图5)施加x方向的水平均布荷载Fx和y方向的水平均布荷载Fy,在xoy平面施加剪切荷载;按照张奇华等[16]的方法对三维数值模型的侧面施加位移边界条件(Sx、Sy)实现,即Sx=4.0 mm,Sy=21 mm。自重通过对三维模型施加重力加速度模拟。

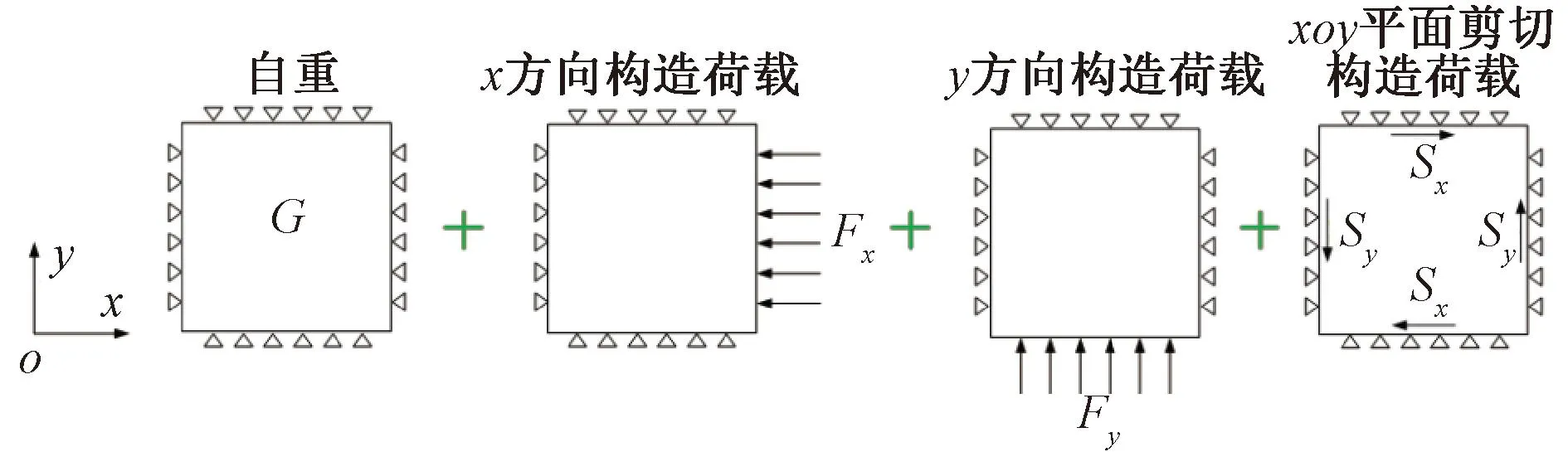
图5 模型边界条件示意

边界位移约束条件:顶面为自由边界,底面施加法向位移约束,侧面除需施加均布荷载面外,其余侧面均施加法向位移约束。

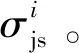
2.5 反演结果及精度验证

基于反演原理,通过施加图5所示的边界条件后,利用式(11)最小二乘法寻优方法可求解得到剔除地温热应力的回归方程为

σhg=1.32+0.9σzz-4.0σx,jb+9.5σy,jb+4.0σxoy

(13)

式中:σzz为自重荷载工况的计算值;σx,jb为x向水平均布荷载的计算值;σy,jb为y向水平均布荷载的计算值;σxoy为xoy面剪切荷载的计算值。

按照回归统计原理,对回归结果进行显著性检验,F显著性统计量F=1.8×10-24小于显著性水平0.01,复相关系数R=0.91≈1,这表明回归值与剔除热应力的实测值之间相关性较高,回归效果较好。

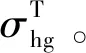
为验证本次反演精度,以埋深最大的DZ-DSFA-01钻孔为例,对比实测值与计算值,见表3,由于切向应力τxy量值较小,因此未参与讨论。岩体热力学参数见表4,则地温热应力σT=0.031×9×10-6×26×103×(H-30)。从表3可知,DZ-DSFA-01钻孔σx分量的平均相对误差为17.8%,σy分量的平均相对误差为19.8%,σz分量的平均相对误差为7.9%,总体平均误差为15.2%,反演精度较为理想。由于该隧道地应力测点较多,限于文章篇幅有限,表5列出了其余钻孔的平均相对误差。由此可知,所有测点的平均相对误差为18.2%,能够控制在20%以下,满足工程建设的需要。

表3 DZ-DSFA-01钻孔实测地应力值与回归值对比

表4 岩体热力学参数

表5 各钻孔平均相对误差

注:σx为x方向地应力值;σy为y方向地应力值;σz为z方向地应力值;左侧应力值代表剔除地温热应力的结果;右侧应力值代表包含地温热应力的结果,相对误差计算公式为:[(|实测值-回归值|)/实测值]×100%,其中应力值均采用表中右侧结果。

DZ-DSFA-01钻孔各测点的地温应力范围为0.9～4.6 MPa,其平均占水平向应力的20.1%,平均占竖向应力的20.5%,由此可见温度应力的占比不容忽视,其将会对岩爆预测产生影响。

3 瞬态岩爆预测

3.1 岩爆模型及边界条件

根据地勘信息,隧道在里程DK281+880—DK282+400,DK283+000—DK283+860,DK284+260—DK284+720,DK286+200—DK286+700四个区段(图1)围岩级别为Ⅲ级,在高地应力环境下存在发生中等岩爆的风险。

为探讨考虑地温热应力下瞬态岩爆烈度问题,采用COMSOL Multiphysics软件热力耦合模块建立岩爆预测数值模型,见图6。数值模型范围取至隧道洞径的3倍,长度约为90 m,高度约为75 m。

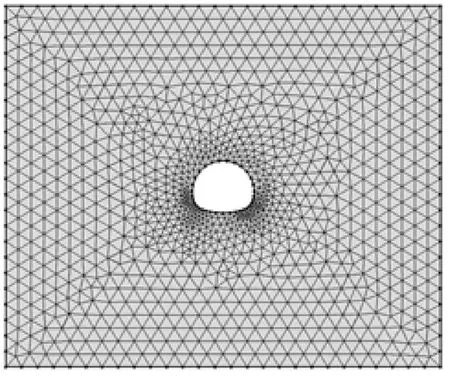
图6 岩爆预测数值模型网格

通过式(13)可以查询DK281+880—DK286+700范围内的地应力回归值,再代入式(12)中,即可求出考虑地温热应力的初始地应力场。将三维数值模型坐标系下的地应力场转化为主应力的形式为

(14)

DK281+880—DK286+700范围内考虑地温热应力的岩体初始地应力场见图7。由图7可知,当埋深增大以后,隧道走线赋存的地应力环境转为以竖向应力为主导,整体呈现σV>σH>σh的特征。

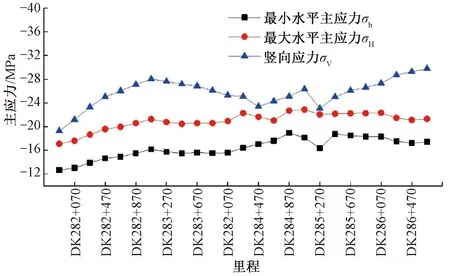
图7 隧道初始地应力场

以隧道里程处对应的初始地应力场作为应力边界条件见图8(a),温度边界条件见图8(c),包括模型初始温度T0和模型边界温度Tb。若是未考虑竖向温度应力的边界条件如图8(b)所示。图8(a)和8(b)中的带下标1和2的应力分量分别为考虑温度应力反演方法的地应力值和未考虑竖向温度应力反演方法的地应力值。考虑隧道洞壁与洞内环境的对流换热过程,对洞壁边界设定对流换热系数qd,热力学计算参数见表4。

图8 模型热力耦合边界条件

围岩初始温度T0和模型边界温度Tb后设为相同值,即T0=Tb,并考虑不利工况的影响取为表4中的最大值。洞内环境温度取洞口全年平均温度(0.3 ℃,地勘资料中洞口气温统计见表6)与洞内施工允许的最高温度[13](28 ℃)的平均值14.2 ℃。考虑热力耦合瞬态求解,得到的应力解带入陶振宇判据[17]进行岩爆烈度预测,见表7。表7中,Rc为单轴抗压强度,里程DK281+880—DK284+720取135 MPa,里程DK286+200—DK286+700取130 MPa,σ1为最大主应力。

表6 洞口近30年月平均气温表

表7 陶振宇岩爆判据[17]

隧道考虑竖向地温应力的瞬态岩爆预测结果见图9,由图9可知,与地勘预测的岩爆烈度不同,在考虑竖向地温应力后,岩爆烈度显著增大,除DK281+880—DK281+900范围处于中等岩爆区外,其余区域均处于强烈岩爆区。

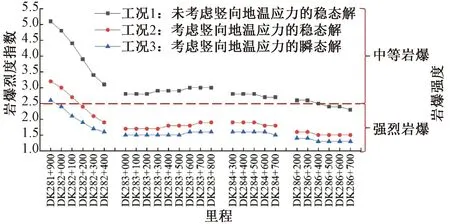
图9 不同方法的岩爆烈度预测结果

4 不同岩爆预测方法的对比分析

以往传统地应力反演方法未考虑地温热应力的影响,反演直接以计算值按照多元回归方法逼近实测值σH、σh、σV(最大水平主应力已包含温度应力,竖向应力未包含温度应力),欠缺了竖向地温应力分量[18-19]。同时,以往求解仅考虑热力耦合的稳态解,对于开挖瞬间的瞬态岩爆烈度还未讨论[20-22]。基于此,共设计3种计算工况岩爆强度(表8),选取四个岩爆区段中最大埋深里程DK282+400、DK283+130、DK284+320、DK286+700为算例进行分析,见表9。

表8 不同工况边界和求解条件

表9 不同工况应力边界条件

按照多元线性回归原理,按传统反演方法再进行一次回归,得到未考虑竖向地温应力分量的回归方程为

σhg=1.7+0.95σzz-2.1σx, jb+12.1σy, jb+6.0σxoy

(15)

工况3已在前文进行了求解,工况2与工况3唯一的不同是其按照稳态求解。工况1按照式(15)可求出各里程对应的岩体初始地应力作为应力边界条件,见图8(b),温度边界条件同样按照图8(c)所示进行施加,考虑稳态进行求解。

图10为里程DK286+700在三种工况下的计算云图。工况1由于未考虑竖向温度热应力的叠加效应,应力边界条件的量值小于其余工况,热力耦合得到的洞壁第一主应力最大值为57 MPa,工况2考虑竖向温度热应力的叠加效应,洞壁第一主应力最大值显著增大至86 MPa,工况3考虑瞬态求解后洞壁第一主应力最大值继续增大,达到102 MPa。这说明,开挖瞬间围岩初始温度与洞内环境温度差值处于峰值状态,此时由温差导致的热应力释放将增大洞壁处的应力集中效应,岩爆烈度将会增强。

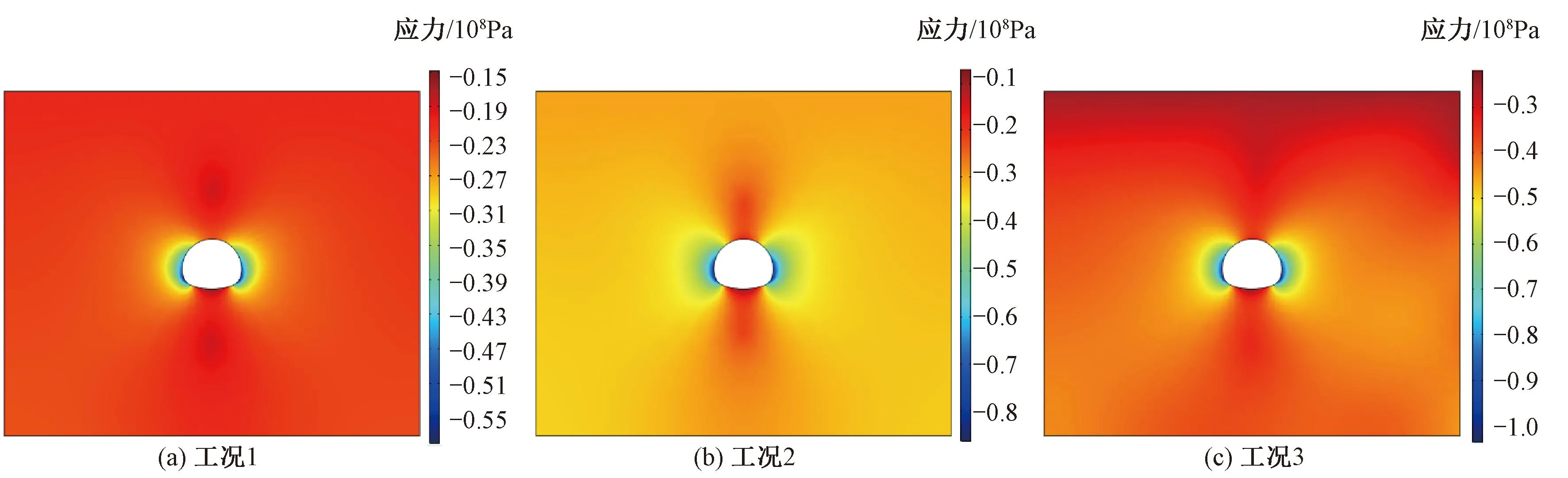
图10 里程DK286+700热力耦合第一主应力云图

四个算例在三种工况下的计算结果见图11。由图11可知,工况1未考虑竖向地温应力稳态解的岩爆预测,除里程DK286+700岩爆烈度指标小于2.5属强烈岩爆外,其余里程岩爆烈度指标均大于2.5,属中等岩爆。工况2考虑竖向地温应力稳态解的岩爆预测,岩爆烈度显著增大,里程DK282+400处岩爆烈度指数由3.1减小至1.9(减幅38.7%),里程DK283+130处岩爆烈度指标由2.8减小至1.7(减幅39.3%),里程DK284+320处岩爆烈度指标由2.8减小至1.9(减幅32.1%),里程DK286+700处岩爆烈度指标由2.3减小至1.5(减幅34.8%),岩爆烈度指标的减小代表岩爆烈度的增加,因此四处里程的岩爆烈度平均增幅为36.2%。工况3考虑竖向地温应力瞬态解的岩爆预测,岩爆烈度继续增强,较工况2岩爆烈度平均增幅为14.2%,较工况1岩爆烈度平均增幅为45.3%。

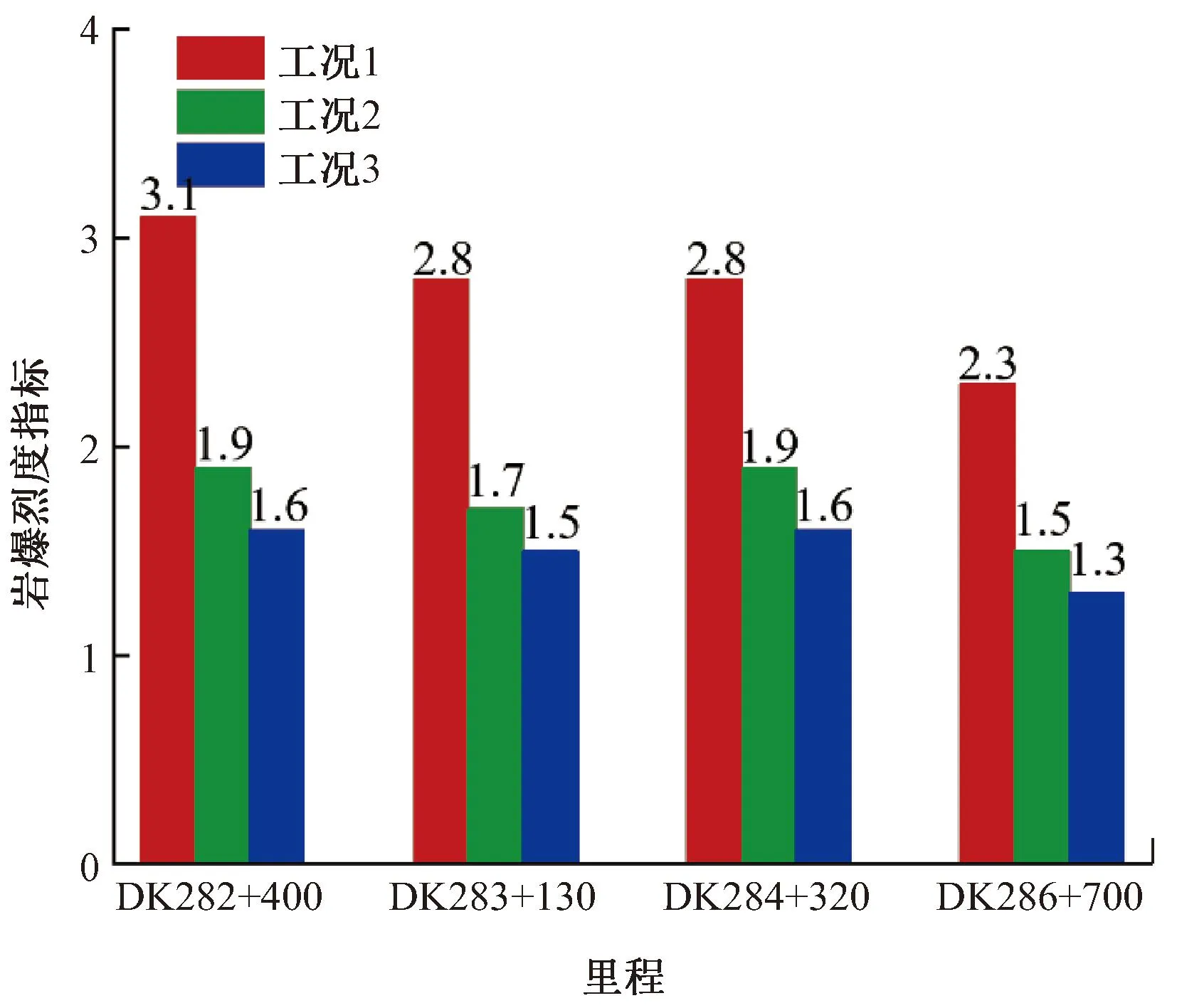
图11 四个算例的岩爆预测结果

此外,按照表8中的三种工况,还计算了隧道四段岩爆区域的烈度指数,见图9。由图9可知,按照工况1即传统的岩爆预测手段,隧道几乎所有岩爆区段都将落在中等岩爆区之内,这与地勘报告的结论相似。工况2考虑竖向温度应力叠加效应后,除DK281+880—DK282+100段落在中等岩爆区内,其余区段的岩爆预测结果均为强烈岩爆。工况3考虑瞬态解后,中等岩爆区域更短,仅DK281+880—DK281+900,其余区段全为强烈岩爆,且岩爆烈度指数小于工况2的结果。

考虑温度热应力的岩爆瞬态预测方法见图12。

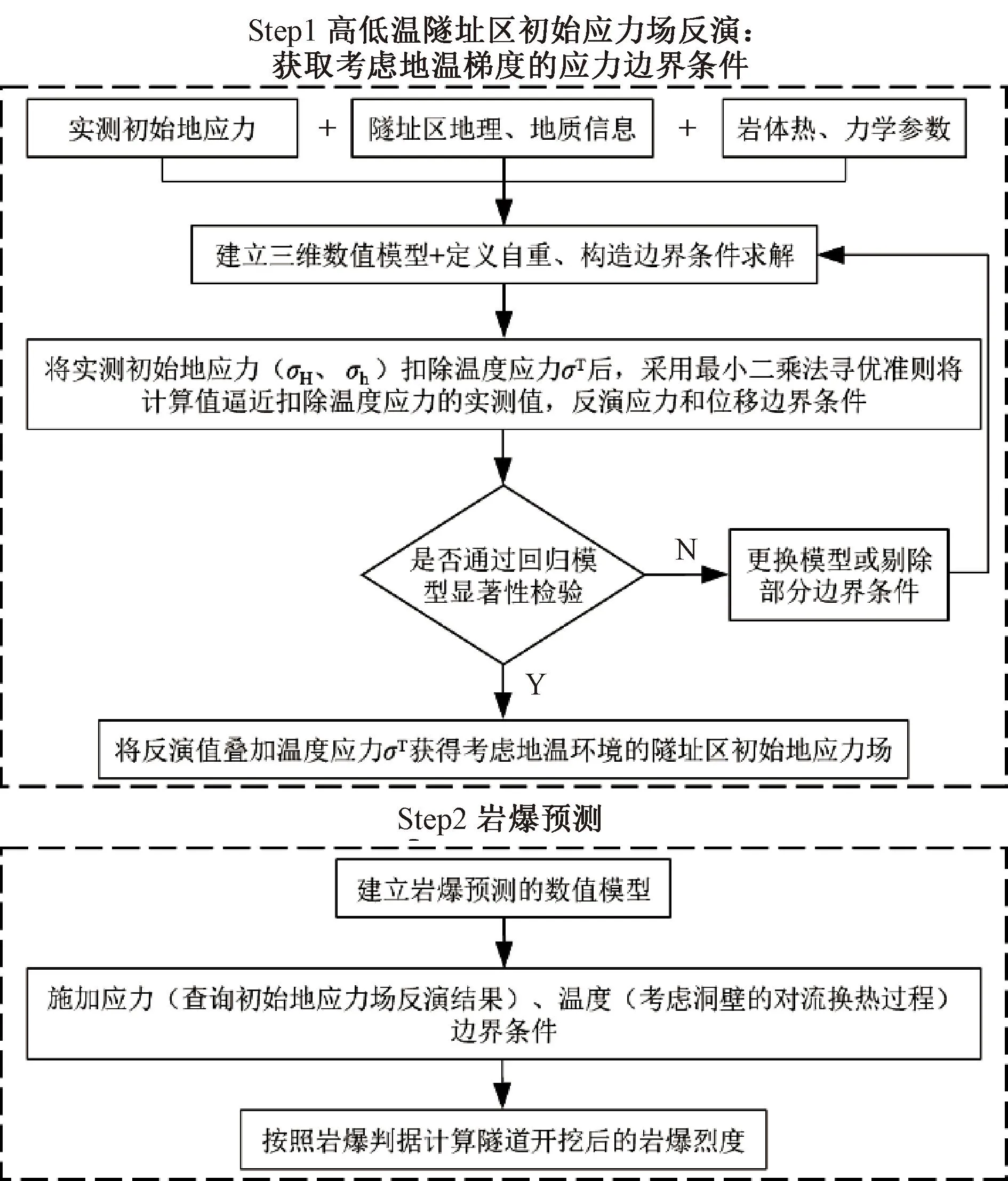
图12 考虑温度热应力的瞬态岩爆预测方法

Step1实测水平主应力剔除温度热应力后与竖向应力一起参与多元线性回归得到反演回归值,将回归值叠加温度热应力后得到岩体初始地应力场。

Step2按照隧道里程提取岩体初始地应力场作为岩爆预测模型的应力边界条件,考虑洞壁与洞内的对流换热过程,以瞬态求解隧道开挖后的洞壁应力值,将其代入岩爆判据中进行岩爆预测。

5 结论

1)水压致裂法的竖向应力(σV=γH)是根据上覆埋深的岩体重力估算而来,未包含温度热应力,因此针对高地温环境的地应力反演应考虑竖向温度热应力的叠加效应。

2)计算表明,康定某隧道由于竖向地温梯度导致的热应力约占水平构造应力的20.1%,约占竖向应力的20.5%,未考虑温度热应力的岩爆预测将会弱化岩爆烈度。

3)未考虑地温热应力的稳态岩爆预测结果与地勘结论吻合(均为中等岩爆)。通过算例的对比分析可知,考虑地温热应力的稳态岩爆预测烈度较传统岩爆预测方法平均增强了约36.2%,而考虑地温热应力的瞬态岩爆预测烈度继续增强了约14.2%。

4)提出的考虑地温应力的热力耦合瞬态岩爆预测方法可修正岩爆预测烈度,对指导相似高地温隧道的岩爆预测具有一定的参考和指导意义。

5)提出的反演回归应力与温度应力叠加的方式获取考虑地温热应力的隧址区地应力场虽原理简便,但过程烦琐。采用热力耦合模型直接参与地应力场反演更加直接,这方面的研究有待下一步开展。