高速列车精确停车的超扭曲非奇异终端滑模控制方法

李中奇，张俊豪，唐博伟

(1.华东交通大学 电气与自动化工程学院，江西 南昌 330013；2.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，江西 南昌 330013)

停车精度是衡量列车自动驾驶(automatic train operation, ATO)系统运行质量的重要技术指标,停车位置的准确性为乘客的舒适和安全带来重要保障,对线路上列车正常、高效运行也起到了关键作用。因此,列车精确停车的深入研究极具重要意义。

目前国内外学者针对列车停车过程中参数不确定性、干扰未知等问题展开了广泛研究。考虑列车停车过程受闸瓦系数、路面参数变化等不确定因素影响,文献[1]提出自适应参数估计的减速度控制方案;文献[2]根据初始状态误差和制动力作为控制输入,提出基于终端迭代学习的列车进站控制方法。由于传统停车控制方法存在适应性差、滞后的问题,文献[3]采用了一种自适应线性自抗扰的停车方法;文献[4]将Picard迭代的辨识方法应用于列车运行控制系统;而在考虑列车停车精度方面,文献[5]采用列车自动进站停车精度预测方法以提高列车停车精度;文献[6]提出鲁棒自触发预测控制方法,通过减少控制输出切换频率以提高停车精度。

上述方法以解决参数不确定性,提升控制精度为目的展开研究,但在列车实际运行过程中,外界不确定性干扰会严重影响系统运行稳定性。为此文献[7]通过设计模糊切换项以补偿列车运行的未知干扰;文献[8]中提出干扰补偿与终端滑模控制结合的方法以增强系统稳定性;在研究永磁同步电机的速度控制系统时,文献[9]中采用结合扰动观测器的终端滑模控制算法以提高系统鲁棒性;对于负载信息未知的二质量伺服系统,文献[10]提出在终端滑模控制方法中引入扩张状态观测器。观测器的引入可使得系统不完全依靠准确的模型来设计控制器,通过对干扰进行估计补偿,以消除其对系统稳定性的影响。

滑模变结构控制因具有较好的鲁棒性和稳定性而被应用于非线性不确定性系统,但其存在的抖振问题限制了滑模方法的应用。文献[11]在研究光电跟踪系统时,为消除抖振提出具有开关型趋近律的分数阶滑模;为实现电机的平滑控制,文献[12]将新型二阶滑模-超扭曲(super twisting, ST)算法应用于电机控制系统;文献[13]中也采用了将超扭曲算法与非奇异终端滑模结合的方法,即有效地解决了奇异性问题,也消除了抖振现象。此外超扭曲算法还成功应用于多智能体系统[14-15];为深入研究超扭曲算法,文献[16]首次提出一种强李雅普诺夫函数以验证该算法的有限时间收敛性质。

本文为提高列车停车精度,针对受外界不确定性扰动影响的列车制动运行系统,利用扩张状态观测器(extented state observer, ESO)对系统未知干扰精确估计作用,结合终端滑模控制具有较好的误差收敛特性,设计出结合扩张状态观测器的超扭曲非奇异终端滑模控制方法。该方法中引入的超扭曲算法对传统滑模控制中的转矩抖振起到了有效抑制作用,采用终端滑模控制实现了系统状态误差收敛值有限时间内趋于零,结合控制方法对未知干扰的观测补偿作用,极大地提高了控制系统稳定性和鲁棒性。并通过李雅普诺夫稳定性理论证明了系统的稳定性,也通过仿真实验对比验证了该方法的精确跟踪能力。

1 列车制动过程的分析建模

制动系统是列车运行安全的重要保证,其在列车停车制动时对列车进行减速控制。列车制动控制原理见图1,在制动时,制动指令无法直接施加在列车动力执行机构上,而是由微制动控制单元接收司机或ATO发出的制动信号,根据列车质量及当前车速,计算出所需制动力,从而改变当前列车的运行状态[17-18]。

图1 列车制动控制原理

本文主要研究自动驾驶控制中制动系统根据目标-距离曲线对制动力的自动计算。现有的制动控制系统并不能控制各车厢的制动力,因此采用单质点建模设计控制器更加贴近现行的应用条件。结合列车运行条件,列车制动过程受力分析见图2[19]。

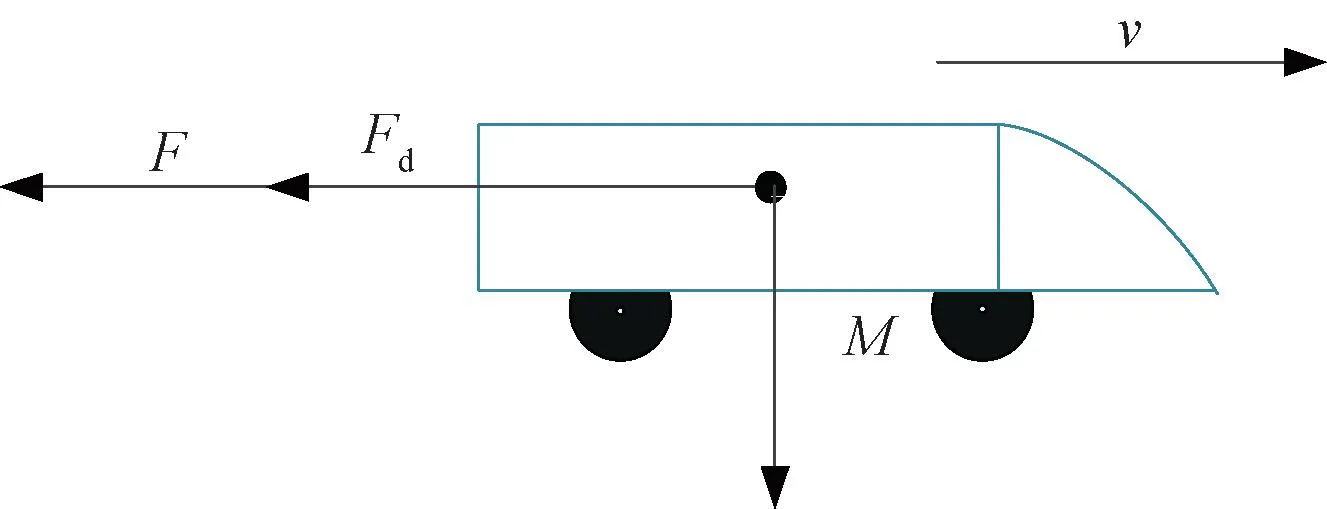
图2 列车制动过程受力分析

列车在制动力F和阻力Fd的共同作用下减速进站停车。根据受力分析,建立其动力学模型为

(1)

式中:X为列车停车距离;M为列车总质量;v为运行速度;F为制动控制转矩;Fd为阻力;Fn为列车基本阻力;Fb为列车运行附加阻力,考虑停车进站过程中,道路环境良好,Fb可忽略不计;D为系统总的不确定性。

2 控制系统设计

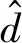
图3 列车制动过程控制系统原理

考虑实际运行环境下,列车容易受到图3中的不确定性干扰影响,从而对列车自动驾驶控制带来不利,因此在方案设计中引入扩张状态观测器对系统未知干扰精确估计,结合控制方法对未知干扰进行补偿,极大地提高了控制系统稳定性和鲁棒性。将设计的观测器和控制器应用于列车制动控制,控制器以系统状态误差作为输入,通过非奇异终端滑模面输入到控制器中计算控制量,扩张观测器对干扰进行估计,并反馈补偿至制动模型以抵消干扰影响。通过闭环控制,使得系统状态误差趋于零,满足了列车停车的精确跟踪、控制输入平滑等要求。

2.1 扩张状态观测器的设计

列车停车制动过程中,极强横向风或不确定性风向会改变阻力计算模型,制动装置的磨损、轮轨磨损等会影响制动力矩的传递,这些时变因素会改变列车制动模型,从而给列车精准施加制动力带来影响[20-21]。本文以列车制动过程动力学方程建立模型,将上述不确定因素定义为影响模型的附加干扰D,其通过影响列车所受总阻力或制动力传递改变列车减速度,从而干扰列车制动力对列车运行状态的控制,给系统运行安全稳定性带来威胁。除了引入扩张状态观测器估计系统受到的外界不确定性干扰D,本文还对系统模型进行补偿以抵消干扰影响,式(1)中的非线性系统为

(2)

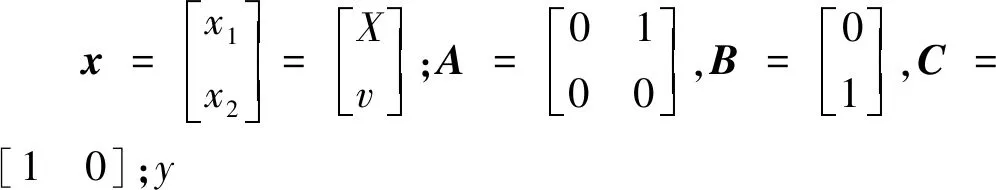
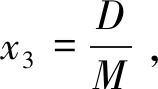
(3)

根据式(3),建立扩张状态观测器

(4)

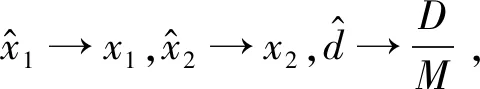
2.2 扩张状态观测器收敛性分析

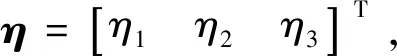
(5)

式中:ε为一个常数,表示系统的运动点趋近滑模面的速率。

同理可得

(6)

(7)

则观测器误差状态方程为

(8)

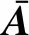
(9)

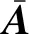
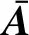
对任意给定的对称正定矩阵R,存在正定矩阵P满足

(10)

定义观测器的李雅普诺夫函数为[23]

V0=δηTPη

(11)

则

(12)

(13)

由式(13)可知,系数δ的大小决定了观测器误差η收敛的速度。系数越小,误差收敛速度越快,且逐渐向零趋近。

2.3 超扭曲控制器设计

设二阶非线性系统为

(14)

式中:u为控制量;p为常系数;f(X)为与X有关的非线性项。

设滑模面为s0=x2+k0x1,其中,k0>0。传统滑模控制当滑模面趋近于0时,状态变量在有限的时间内达到平衡点,系统到达稳定状态[24]。但为了更好的消除抖振现象,依据上述二阶系统模型,设计超扭曲滑模控制器为

(15)

式中:k3和k4为大于0的常数;符号函数的引入使得u1为滑模的非线性间断函数;u2为滑模变量积分值。由于式(14)所表示的控制量是连续函数,所以二阶滑模控制消除了传统滑模的抖振问题,使得滑模面能保持稳定,提高系统控制性能。稳定性证明见文献[16]。

2.4 超扭曲非奇异终端滑模控制器设计

高速列车在运行时,不确定因素的影响使得系统稳定性下降。考虑其受到外界不确定性干扰后得到列车制动过程的速度、位移状态误差模型为

(16)

式中:x为列车实际制动距离;xd为给定制动距离。

在传统滑模面s0=e2+k0e1的基础上,结合位置和速度两者状态误差,引入符号函数部分设计非奇终端滑模面解决传统滑模方法,无法使得系统状态误差在有限时间内收敛至零的问题,两个符号函数部分由符号函数与绝对值幂次乘积的形式构成非线性函数,替代了传统终端滑模单一的幂次函数形式,避免复数形式的出现,克服系统出现奇异性问题,最终设计非奇异终端滑模面为

s=e1+k1|e1|asgn(e1)+k2|e2|bsgn(e2)

(17)

式中:k1和k2均为正奇数。

(18)

式中:a、b为常数,01。

结合超扭曲滑模控制器可有效消除抖振的优点,将超扭曲滑模控制器作为切换控制部分,以式(17)为滑模面s,设计uw为

(19)

式中:k3和k4均为大于0的常数。

因此,所设计的超扭曲非奇异终端滑模控制器的控制律为

(20)

结合扩张观测器对于系统总的不确定性干扰的估计,通过干扰补偿以此提高系统鲁棒性,控制系统总控制律为

(21)

2.5 稳定性证明

针对上述列车制动运行控制系统进行稳定性分析,构造李亚普诺夫函数为

(22)

对s求导得

(23)

由此可得

s(e2+k1a|e1|a-1e2)

(24)

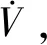
(25)

当式中e1和e2为任意值时

s[(e2-|e2|)(1+k1a|e1|a-1)]≤0

(26)

又由非奇异滑模面s的设计可知

(27)

最后根据扩张状态观测器的状态误差收敛为零可知

(28)

将式(21)代入式(16),可得

(29)

当e2=0时,有

(30)

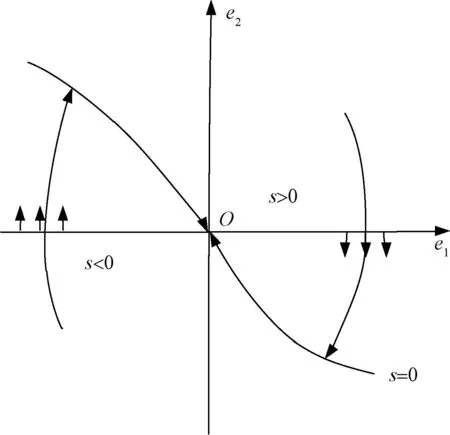
图4 系统的相轨迹

3 仿真验证与结果分析

为验证本文所提出方法中扩张状态观测器对增强系统抗干扰能力的作用,选取未做干扰补偿的超扭曲非奇异终端滑模控制(Super Twisting Nonsingular Terminal Sliding Mode Control, ST-NTSMC)方法进行对比。为验证本文方法在停车精度和误差收敛上优越性,选取结合扩张状态观测器的传统滑模和ESO-PID进行对比[26]。以列车制动模型为基础,设计Simulink仿真系统见图5。高速列车模型部分参数设定如表1所示[27-28]。

表1 列车模型部分参数

图5 ESO-ST-NTSMC的Simulink仿真框图

模拟实际高速列车停车制动过程,设计停车过程的时间-速度曲线分段函数为

(31)

定义干扰信号为

(32)

3.1 扩张状态观测器有效性的验证

为验证扩张状态观测器对于外界不确定性干扰观测的有效性,模拟实际运行中可能存在的干扰情况,在模型中分别加入干扰1(f1=0.1sin(2t))和干扰2(f2=0.1rand(1))两种不同类型干扰。运行仿真程序,扩张状态观测器观测结果见图6,由图6(a)、图6(b)中的局部放大图可知,在分别加入正弦信号和随机信号的系统中,观测器均能在较短时间内实现收敛,实现了未知干扰的快速估计。

图6 干扰观测结果

3.2 控制方法对比验证

各方法参数设定如下:

1)本文方法ESO-ST-NTSMC:k1、k2、a,b为非奇异终端滑模面参数,k3和k4为超扭曲滑模控制器参数。k1=10、k2=50、a=1.5、b=2、k3=2、k4=3、干扰为f。

2)方法二ST-NTSMC:较方法一,方法二在设计时,删除了扩张观测器设计部分,其余参数设计不变。k1=10、k2=50、a=1.5、b=2、k3=2、k4=3、干扰为f。

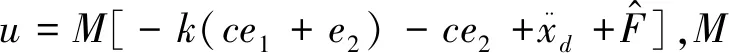
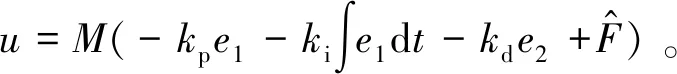
依据上述参数设定分别将各方法应用于列车制动控制系统,在均取得良好控制效果的前提下,各方法实际控制效果见图7～图10。

图7 控制转矩结果对比

为验证本文方法在提高系统抗干扰能力和消除控制转矩抖振上的优越性,将各方法的输出控制转矩进行对比,结果见图7。由局部放大图可知,ST-NTSMC方法受扰动影响,控制转矩出现跳变,且波动幅度较大,使得列车运行舒适度不佳。本文方法与引入扩张观测器的方法三ESO-传统滑模和方法四ESO-PID能够对系统干扰实时观测并有效补偿,有效避免了不确定性扰动的影响,三种控制方法均具有较好的抗干扰能力,相比于传统滑模方法,本文方法转矩输出平稳,实现了制动运行的平滑控制。

列车完成停车制动后,各方法的速度-距离制动曲线见图8。由图8可知,初始阶段ESO-传统滑模方法和ESO-PID方法的制动曲线贴近参考制动曲线,但在运行一段时间后,各方法均处于较好的制动运行状态,实现了列车目标制动曲线的良好跟踪控制。另由局部放大图可以看出,本文方法ESO-ST-NTSMC在运行过程后期,其制动曲线更为贴近参考制动曲线的运行轨迹,停车制动过程更为精准。

图8 状态跟踪效果对比

为进一步探讨各方法的停车性能,验证本文方法具有解决传统滑模方法存在的状态误差无法在有限时间内收敛至零的问题。各方法的速度与位移误差对比见图9,由图9可知,在得到扩张状态观测器对于系统干扰的精确估计并补偿的作用下,方法三的位移误差在有限时间内一直稳定在0.13 m左右,且相比于其他对比方法,本文方法在采用超扭曲非奇异终端滑模控制后,位移误差在有限时间内收敛趋于0值。

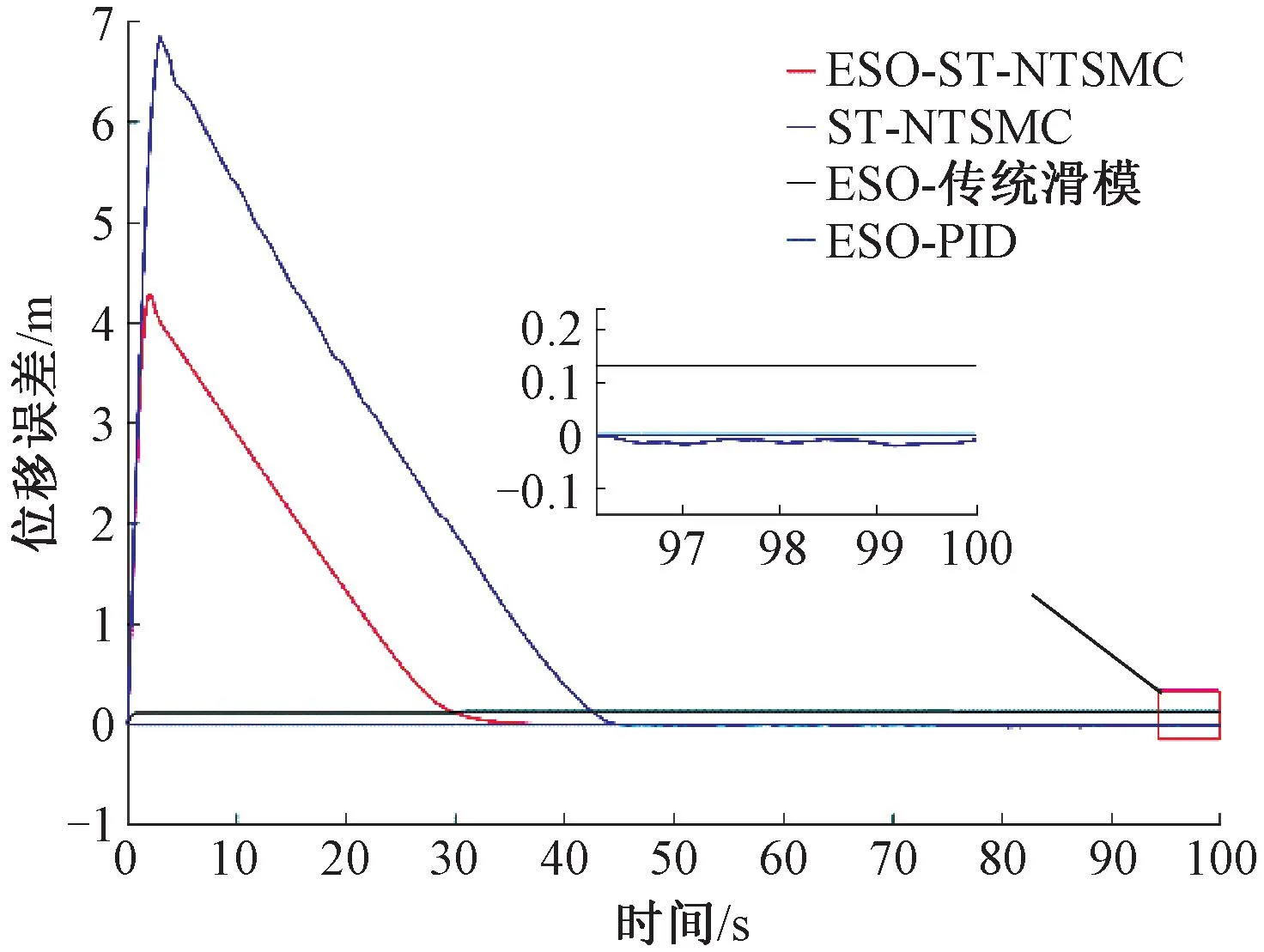
图9 位移误差对比

图10为速度误差对比。由图10可见,列车运行过程中,各方法的速度误差均满足状态跟踪要求。初始阶段时,方法三和方法四在误差和收敛性上具有一定优越性,系统稳定运行一段时间后,各方法误差均收敛到较小数值,实现了较好的制动跟踪控制。由局部放大图可以看出,在运行阶段末期,本文方法的跟踪误差数值收敛于极小值,验证了本文方法在列车停车过程中状态跟踪的优越性能。

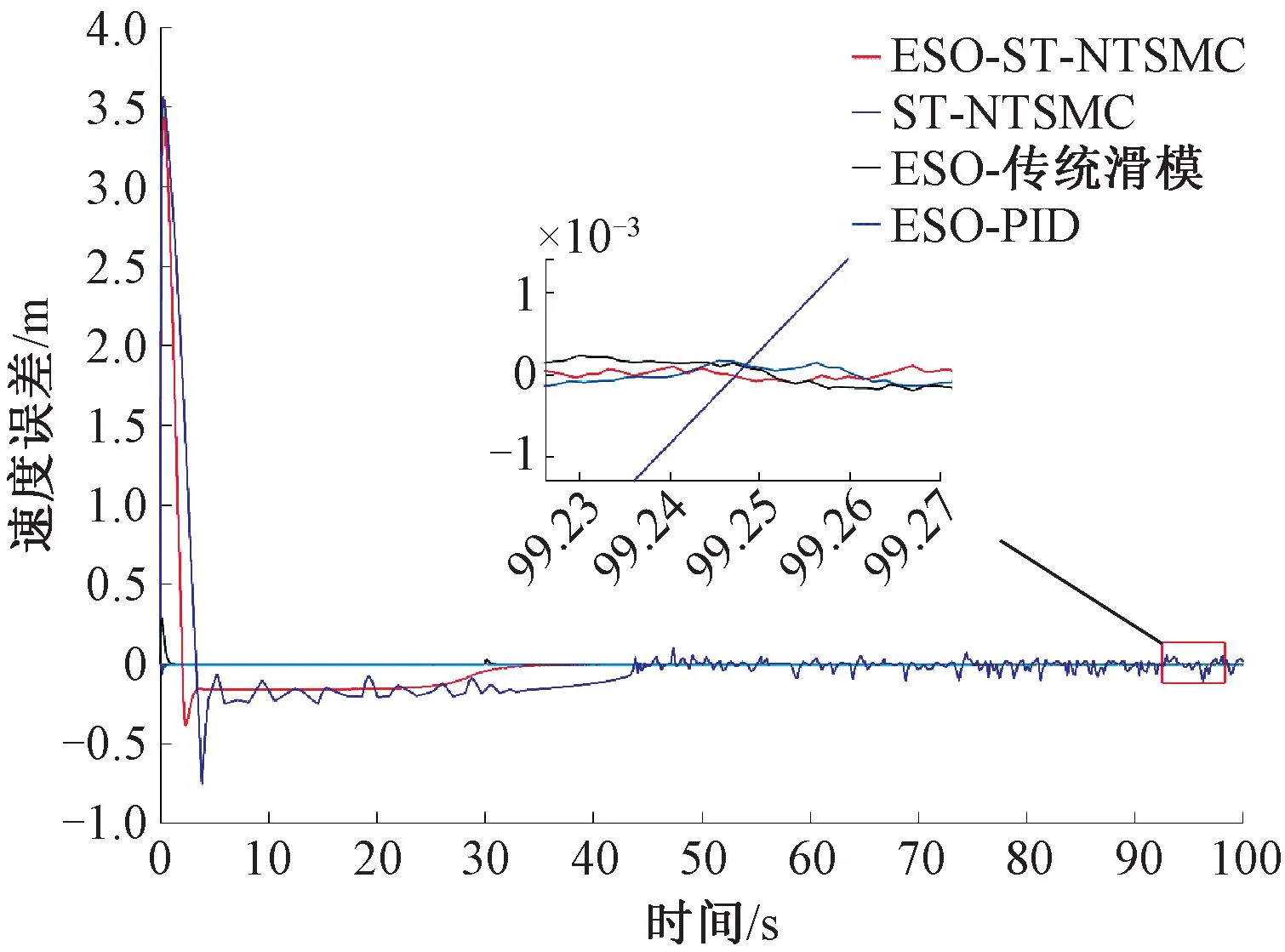
图10 速度误差对比

为直观的看出本文方法与对比方法在停车精度上的优越性,以表1中设定的3 777.5 m为参考制动距离,各方法的停车制动距离误差结果如表2所示,可以得出本文方法的列车精确停车控制具有更高精度。

表2 停车误差

4 结论

本文结合列车制动模型,以实现列车制动过程的精确停车为目的,为减少外界不确定性干扰对系统的影响,从而提高停车精度,提出了超扭曲非奇异终端滑模控制与扩张状态观测器结合的方法。引入的观测器能够有效估计系统状态和外界不确定性干扰,增强了系统鲁棒性。采用超扭曲非奇异终端滑模控制器消除了控制转矩的抖振,实现了列车运行状态误差在有限时间内收敛至零。通过与其他控制方法的对比可知,本文方法的控制输入平滑,抗干扰能力更强,跟踪误差小,具有更高停车精度,实现了列车的精确停车控制,充分验证了本文方法的优越性。

本文主要以解决外界不确定性干扰对运行系统影响,增强系统鲁棒性和实现系统控制平滑为研究目标。在之后的研究中,作者将参考文献[29-30],考虑添加运行附加阻力和制动过程时滞的对列车影响。