考虑补贴退出的中欧班列多主体策略演化博弈
冯芬玲,张 泽,蔡明旭
(中南大学 交通运输工程学院,湖南 长沙 410075)
在“一带一路”倡议的影响下,中欧班列作为便利快捷的新型国际运输组织方式[1],截至2023年9月,累计开行7.7万列,运送货物731万标箱,通达欧洲25个国家和地区的217个城市,以及沿线11个亚洲国家和地区超过100个城市[2]。中欧班列运营市场规模的提升吸引平台企业、托运人等多种利益相关群体加入,形成活跃的市场生态圈[3]。但在市场培育初期,地方政府将发运箱数作为单一补贴依据为中欧班列提供高额补贴,导致出现无序竞争、低价揽货、空箱返回等现象,不符合市场运行的客观规律[4],阻碍了中欧班列可持续发展。
为解决以上问题,国家财政部门计划实行补贴退出政策,但补贴退出势必会对现有货源基础产生影响[5],多地补贴退出政策并未落实[6]。究其原因,是因为补贴涉及多个利益相关方,单一从地方政府角度并不能实现中欧班列市场化运营目标,因此有必要对中欧班列运营市场中多个主体在补贴退出背景下的策略演变展开研究,形成科学的补贴退出方法。
很多学者针对中欧班列补贴问题展开了大量研究。市场培育初期,大多数研究运用二元Logit模型[4]、多目标优化理论[7]等方法聚焦于探究补贴对中欧班列运营市场的影响。随着市场发展,逐渐有学者将博弈论运用到中欧班列补贴研究中,Kundu等[8]运用博弈论方法建立铁路与海运的竞争模型,分析补贴对托运人运输方式选择的影响。张蒙蒙等[9]考虑地方政府将社会福利最大化作为补贴目标,建立竞合博弈模型,探究地方政府与平台公司两个层面的竞争与合作决策。Ma等[10]针对两条相邻线路建立非合作博弈模型,认为政府补贴是影响定价的主要因素。综上,现有研究大多围绕中欧班列与海运、中欧班列线路之间的竞合关系,提出中欧班列的补贴策略,通常忽视货物时间价值特性,并且少有研究从补贴行为的直接利益相关者角度探究中欧班列运营市场的演变,而演化博弈论在探究多个种群的动态博弈方面具有优越性。
本文考虑补贴退出的影响以及货物时间价值,构建中欧班列运营市场中地方政府、运营平台企业、托运人之间的演化博弈模型;将调研与仿真结合,验证模型有效性,并分析不同情形下相关因素对演化系统的影响,研究成果可为中欧班列补贴退出背景下各利益相关主体的策略选择提供借鉴。
1 模型建立
1.1 问题描述及模型建立
中欧班列运营市场模式见图1。由图1可见,地方政府、运营平台企业与托运人三者是中欧班列运营市场发展过程中非常重要的利益相关者。

图1 中欧班列运营市场模式
演化博弈论是探究多个相互作用的物种组成的种群动态演化的理论,主要基于有限理性假设,聚焦于群体长期行为演化的过程。本文运用演化博弈论,认为地方政府、中欧班列运营平台企业、托运人3个群体是以自身利益最大化为目标的有限理性主体,各主体之间信息不对称,群体内部的各个个体之间存在模仿、学习、交流等动态交互决策过程,构建三者之间“补贴-运营-托运”策略的演化博弈模型:
1)博弈主体行为策略,A为地方政府策略集,表示政府补贴或不补贴中欧班列,A={SA1,SA2};B为中欧班列运营平台企业策略集,表示企业运营或不运营中欧班列,B={SB1,SB2};C为托运人策略集,表示选择或不选择中欧班列托运货物,C={SC1,SC2}。非对称多群体演化博弈系统不能在混合策略处达到长期演化稳定状态[11],故假设策略集中策略都为一对互斥的纯策略。
2)各个纯策略对SA1和SA2、SB1和SB2、SC1和SC2分别在三方群体中被选择的概率为x和1-x、y和1-y、z和1-z。因此,该中欧班列运营市场三方演化博弈系统的决策空间可以定义为Ø={(x,y,z)|x∈[0,1],y∈[0,1],z∈[0,1]}。
3)Q(q1,q2)为中欧班列运营的集装箱货运量,q1为固定运输量;q2为弹性运输量,即托运人受价格等影响可以在中欧班列、航空或水上运输中选择的货运量。
4)对于地方政府而言,企业运营给当地带来人口就业、税收、经济拉动作用形成的社会效益抽象表达为M1;托运人持续托运货物促进各物流园区的落地,从而形成的社会效益抽象表达为M2。地方政府对中欧班列的补贴有两种形式,按照运量直接补贴给中欧班列运营平台企业,补贴金额N1为
N1=N0(q1+q2)φ1
(1)
式中:N0为基础直接补贴金额;φ1为直接补贴退出率[12]。
地方政府也会通过退税等方式间接补贴给托运人企业,其补贴金额N2为
(2)

地方政府会有一定的概率γ,γ∈[0,1],对企业与托运人运营中欧班列以及托运情况进行监察,监管成本为D0,若企业存在未运营中欧班列但领取补贴的行为,假设监管一定会被查出,追回补贴N1,并处以罚金H1;托运人存在未托运但领取补贴的行为,追回补贴N2。
5)对于中欧班列运营平台企业而言,地方政府对企业的直接补贴行为会直接作用于降低运价,fi为中欧班列集装箱运价,i=1为地方政府补贴时的中欧班列运价,i=2为不补贴时运价;c为中欧班列的综合运输成本;I为不开展中欧班列业务时,企业开展其他货运代理业务的收入,CI为此时业务成本;当托运人已经托运但企业没有运营组织中欧班列,造成的品牌形象损失为K。
6)对于托运人,P为运输货物的目标货值。当托运人选择中欧班列托运,但企业没有运营组织发运列车,此时造成赔付E1为
E1=αPQ
(3)
式中:α为企业对托运人的赔付率。
中欧班列运输相比于海运与空运分别有运输时间与运输费用上的优势[2],托运人选择海运或空运会造成货物时间价值的损失或运输费用的提高,造成的托运成本的提高Cw(Q)为
Cw(Q)=θ1Ca+θ2Cb
(4)
Ca=βtQ
(5)
Cb=Q(cair-c)
(6)
(7)
式中:θ1为不选择中欧班列时托运人偏好选择海运的权重系数;θ2为不选择中欧班列时托运人偏好选择空运时的权重系数;Ca为海运相比于中欧班列损失的货物时间价值;Cb为空运相比于中欧班列增加的运输费用;β为单位时间价值;t为增加的运输时间;cair为空运运输成本;λ为货物性质系数;S为社会折现率[13]。
7)根据模型中各参数定义,0
1.2 支付矩阵的构建
由上述问题假设可得三方博弈支付矩阵见表1。

表1 中欧班列运营系统三方博弈主体支付矩阵
2 模型求解
2.1 博弈主体策略稳定性和演化路径分析
复制动态方程是演化博弈理论中的核心动力学机制,相较于其他纳什均衡选择机制,可用于描述参与人根据过去多次博弈结果调整策略选择的动态过程,即有限理性参与人的行为变化趋势[14-15]。所以建立三主体的策略选择复制动态方程。根据李雅普诺夫稳定性定理,复制动态方程的平衡点稳定应该满足两个条件:F(x)=0,dF(x)/dx<0[16]。
1)地方政府的期望收益与复制动态分析
地方政府选择SA1策略的期望收益UA1为
UA1=yz{M1+M2-(q1+q2)[N0φ1+
(1-y)z{-M1+M2+(q1+q2)[(γ-1)N0φ1-
(8)
地方政府选择SA2策略的期望收益UA2为
UA2=yz(M1+M2-γD0)+y(1-z)(M1-M2-γD0)+(1-y)z(-M1+M2-γD0)+(1-y)·
(1-z)(-M1-M2-γD0)
(9)
(10)
地方政府复制动态方程为
(11)

(N1-H)γy+(γ-1)(N1+N2)+γH}
(12)

综上,地方政府的演化稳定趋势见图2。
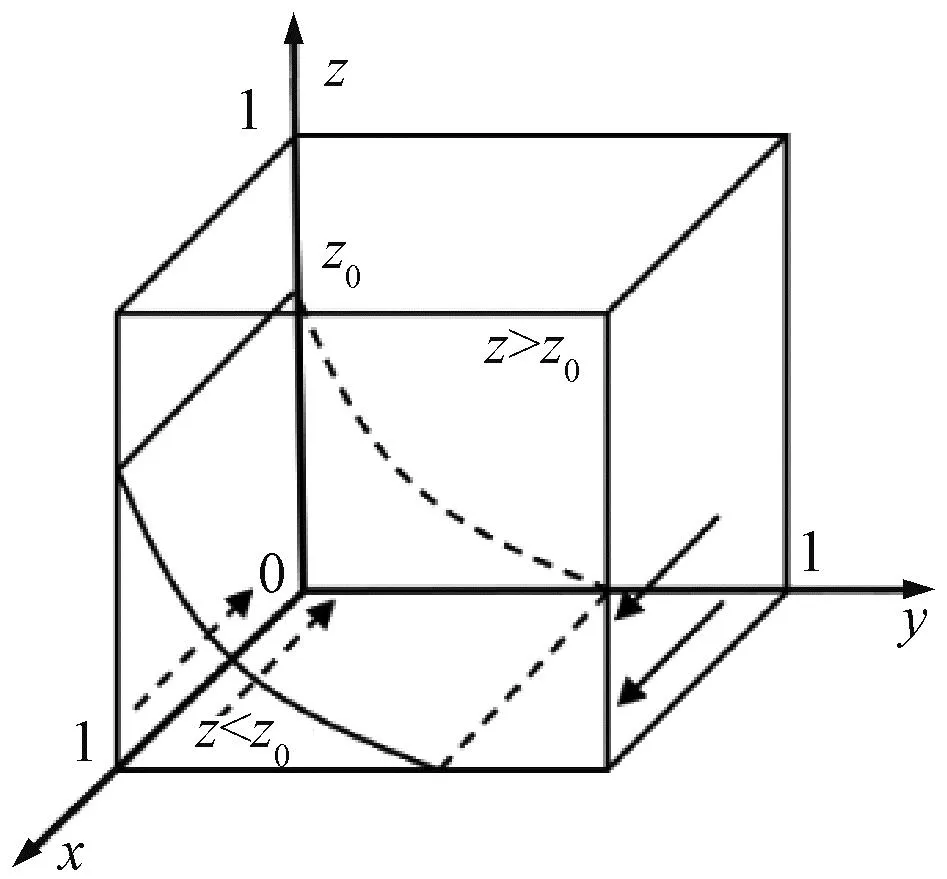
图2 地方政府策略演化趋势
2)运营平台企业的期望收益与复制动态分析
运营平台企业选择SB1策略的期望收益UB1为
UB1=xz[(q1+q2)(f1-c+N0φ1)]+x(1-z)
[q1f1+(q1+q2)(-c+N0φ1)]+(1-x)
z[(q1+q2)(f2-c)]+(1-x)(1-z)
[-(q1+q2)c+q1f2]
(13)
运营平台企业选择SB2策略的期望收益UB2为
UB2=xz{I-CI-K+(q1+q2)[N0φ1(1-γ)-αp]-
γH}+x(1-z)[I-CI-K+N0φ1(q1+q2)(1-γ)-
γH-αpq1]+(1-x)z[I-CI-K-αp·
(q1+q2)]+(1-x)(1-z)(I-CI-K-αpq1)
(14)
运营平台企业平均收益为
(15)
运营平台企业的复制动态方程为
y(1-y){xγN0φ1(q1+q2)+x[(f1-f2)(zq2+q1)]+
xγH+(f2+αp)(zq2+q1)-c(q1+q2)-I+CI+K}
(16)
令σ1=zq2+q1,并代入N1=N0(q1+q2)φ1,并对F(y)关于y求一阶偏导得
σ1(f2+αp)-c(q1+q2)-I+CI+K}
(17)
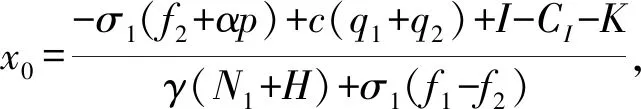
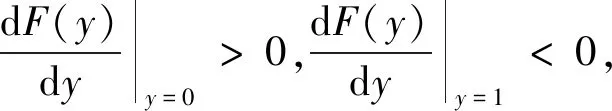

综上,中欧班列运营平台企业的策略演化趋势见图3。
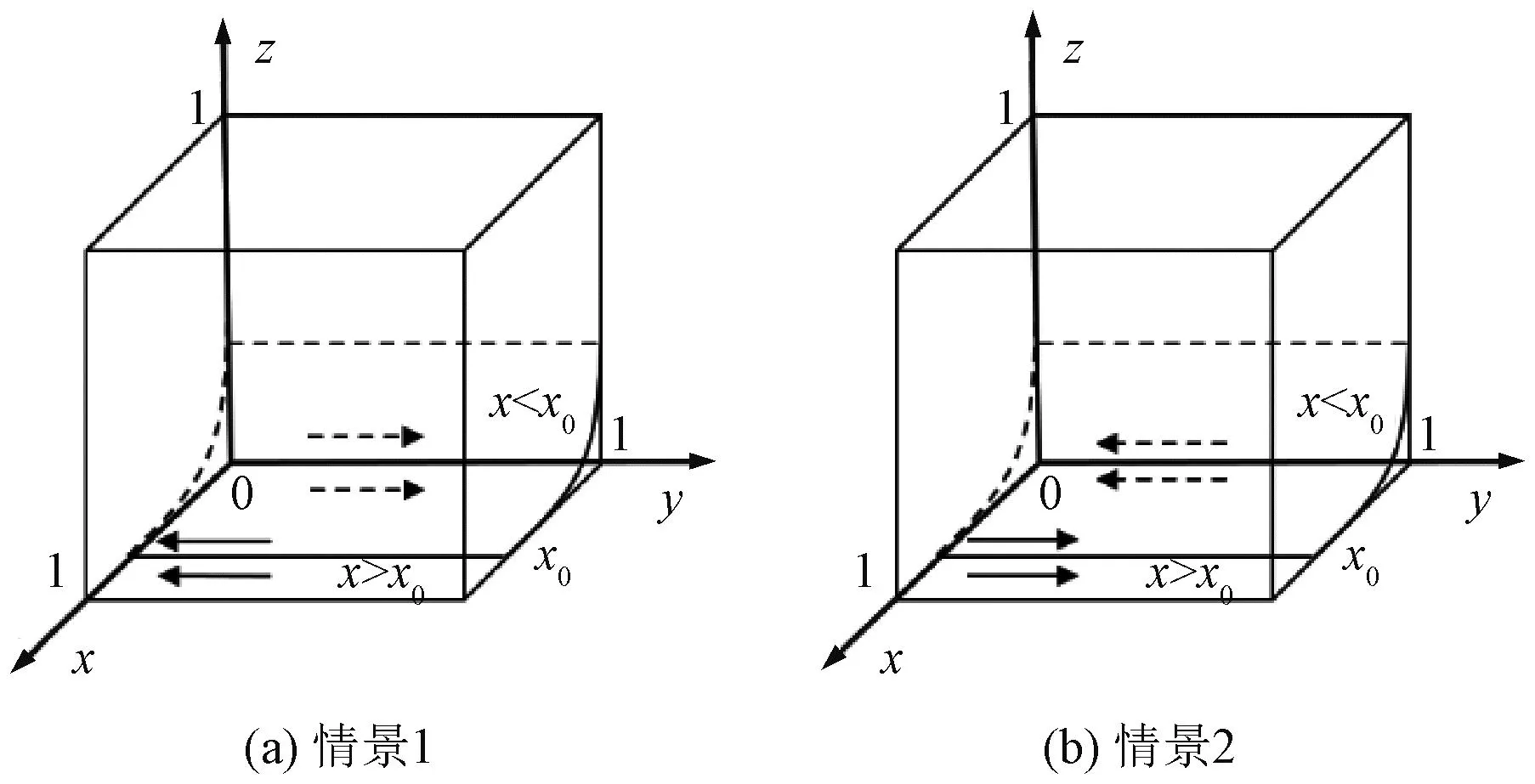
图3 中欧班列运营平台企业策略演化趋势
3)托运人的期望收益与复制动态分析
托运人选择策略SC1的期望收益UC1为
(q1+q2)(p-f2)+(1-x)(1-y)(q1+q2)(αp-f2)
(18)
托运人选择策略SC2的期望收益为UC2
Cw(q2)}+x(1-y){(q1+q2)[-f1+p+(1-γ)·
y[(q1+q2)(p-f2)-Cw(q2)]+(1-x)(1-y)·
[(q1+q2)(p-f2)-Cw(q1+q2)+αpq1]
(19)
托运人平均收益为
刘雅鸣在讲话中强调,要科学谋划,着力打牢水情教育工作的基础。要充分利用第一次全国水利普查的数据成果,结合全球经济社会发展、气候变化、资源利用、生态保护等相关数据,掌握我国基本水情的关键数据,动态更新,持续积累,确保水情教育的权威性、有效性。要广泛深入开展调查研究,抓紧水情教育规划编制,找准水情教育工作切入点,有力有序有效推进水情教育工作。
(20)
托运人的复制动态方程为
(q1+q2)+αpq2+p(q1+q2)+Cw(q1+q2)]
(21)

xγN2+p(q1+q2+αq2)+Cw(q1+q2)}
(22)
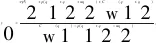
综上,托运人的演化稳定趋势见图4。
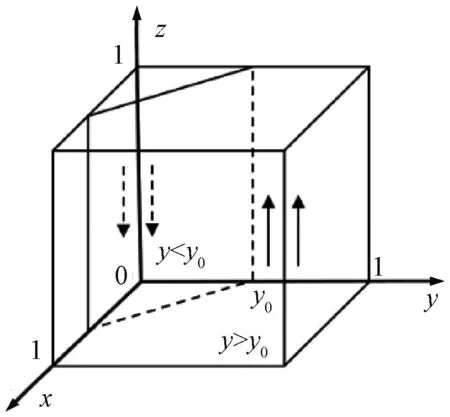
图4 托运人策略演化趋势
2.2 博弈系统的演化策略稳定性分析
2.1节分析了单个博弈主体策略演化过程,但中欧班列运营市场的发展为地方政府、运营平台企业以及托运人三方的共同作用。通过Jacobian矩阵分析可以得到的三方演化博弈系统的演化稳定策略,联立三者的复制动态方程式(11)、式(16)、式(21)形成中欧班列运营市场复制动态系统(I)。
(23)
系统(I)的Jacobian矩阵为
(24)
由式(23)可得系统的8个纯策略纳什均衡点为:X1(0,0,0)、X2(0,1,0)、X3(0,1,1)、X4(0,0,1)、X5(1,0,0)、X6(1,1,0)、X7(1,0,1)、X8(1,1,1)。由李雅普诺夫第一方法可知,雅克比矩阵的所有特征值具有负实部时,均衡点才是系统的演化稳定策略。故将上述8个纯策略均衡点分别代入系统的雅克比矩阵式(24),可得到均衡点的Jacobian矩阵特征值见表2,根据特征值情况对系统稳定性进行讨论。

表2 博弈系统Jacobian矩阵特征值
由各参数取值范围,计算得X1(0,0,0)以及X5(1,0,0)的特征值恒为正值,故X1、X5两点不是系统演化稳定点,讨论得6种演化情形。
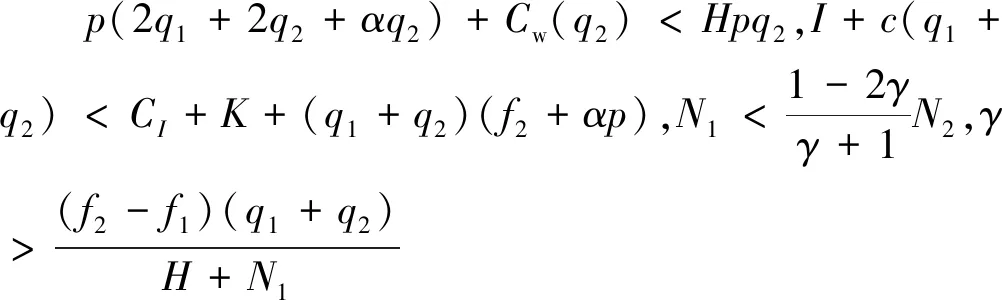
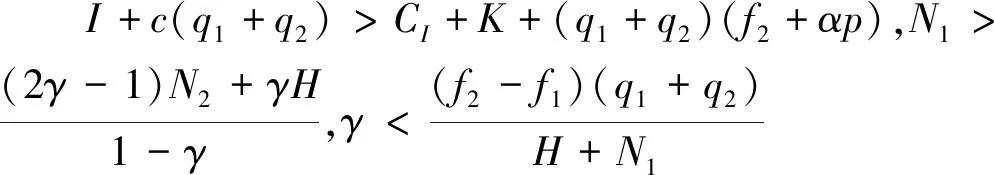



3 仿真分析
为验证演化稳定性分析的有效性,结合调研现实情况对各参数赋以数值,并利用Matlab R2022a进行数值仿真。
3.1 数据集调研
通过调研TCL公司运量,查阅武汉、重庆、长春、郑州、南京等多个城市中欧班列发展绩效审计报告、退税公告、聘请第三方机构监管的招标公告等,确定各常态化开行中欧班列城市中对班列发展进行监督审计的城市比例,从而确定政府监察率γ=45%。通过电话调研得出2022年10月各个中欧班列运营平台公司“郑州—马拉舍维奇”站到站运输价格f1,取其平均值为54 300/FEU。对托运人企业进行问卷调查,结合既有研究[13],运用层次分析法确定托运人在不选择中欧班列时选择海运或空运托运货物的偏好权重分别为θ1=0.615 9,θ2=0.384 1。
最终确定不同运营情形下的关键参数取值。

数组2:φ1=30%,φ2=10%,H=1元/FEU,其他数据与数组1相同,H=1元/FEU与其他数据具有明显的量级差距,该取值意味着不进行骗补罚款。
3.2 模型验证
由2.2节演化稳定性分析,同时考虑中欧班列的发展愿景是企业积极运营,托运人持续托运,地方政府不补贴的理想发展状态,本文选择对市场的愿景情形2以及现状情形6进行演化仿真,见图5、图6。从决策空间Ø={(x,y,z)|x∈[0,1],y∈[0,1],z∈[0,1]}内随机取值,分别对情形2与情形6经过729次重复演化博弈动态仿真,结果如图5(a),图6(a)所示,同时为清晰展现演化过程,在决策空间内随机生成一组初始决策的演化仿真结果如图5(b),图6(b)所示。

图5 情形2的数组1下系统演化博弈仿真
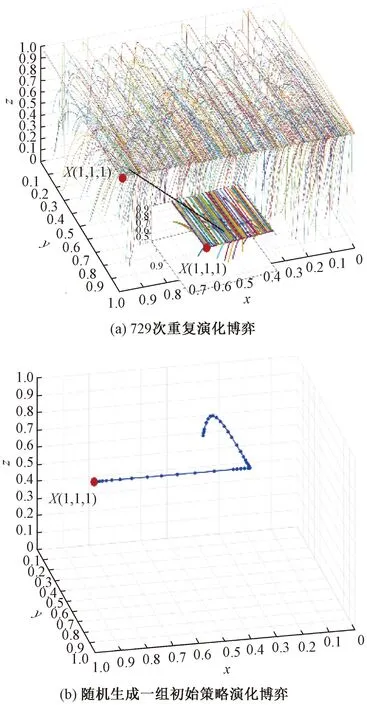
图6 情形6的数组2下系统的演化博弈仿真
对于数组1,当φ1<1.64φ2、H>2.6N0(q1+q2)时满足情形2的条件。由图5可知,最终系统策略演化至X3(0,1,1),即:(不补贴,运营,托运)。对于数组2,当φ1>1.64φ2、0 综合模型验证结果,可以看出两种情形下托运人与运营平台企业形成响应速度快于整体系统的子演化系统,由此构成刚性演化系统。对比两种演化情形,只有采取骗补惩罚,惩罚金额大于2.6N0(q1+q2),且对企业与托运人的补贴退出速度基本同步时,中欧班列演化系统才能彻底演化至完全市场化的不补贴状态,该结果与一些研究提出的中欧班列空载惩罚系数[17]的概念相符合。 在原数组1、数组2的基础上,为消除初始策略选择概率对系统演化的影响,将三方主体的初始策略选择概率分别取值x=0.5,y=0.5,z=0.5,再分别改变相关因素的取值,仿真取值变化时的主体策略选择概率演化情况。 3.3.1 地方政府补贴退出率φ1、φ2 为探究情形2下补贴退出率的φ1、φ2对系统演化结果的影响,在数组1基础上令补贴退出率取值分别为φ1=φ2=0.4,φ1=φ2=0.6、φ1=φ2=0.8,仿真结果见图7。 由图7可知,在具有骗补惩罚H且φ1<1.64φ2的前提下,即对企业与托运人的补贴退出速度基本同步且补贴退出率为40%时,企业与托运人的策略选择概率很快演化至1,但不同补贴退出力度下系统演化至稳定策略点X3(0,1,1)的演化时间差异较小。结果表明情形2下补贴退出率的变化主要影响中欧班列运营平台企业与托运人,且随着补贴退出率的降低,实际补贴金额不断减少,促进了运营平台企业与托运人的策略选择过程;同时,为了形成中欧班列完全市场化的发展目标,需要保持较快的补贴退出速率。 为探究情形6下补贴退出率φ1、φ2对系统演化结果的影响,在数组2基础上,令补贴退出率取值分别为φ1=0.3、φ2=0.1,φ1=0.4、φ2=0.2,φ1=0.5、φ2=0.3,仿真结果见图8(a),由于运营平台企业与托运人策略很快演化至1,为探究稳定策略X8(1,1,1)附近的演化规律,绘制x-t平面见图8(b)。 图8 情形6的数组2下补贴退出率对系统演化结果的影响 由图8可知,在没有骗补惩罚且φ1>1.64φ2的前提下,即地方政府对企业的补贴退出速度慢于托运人时,φ1=0.3、φ2=0.1中欧班列运营系统到达演化稳定策略X8(1,1,1)的速度更快。结果说明中欧班列运营系统现状下,地方政府对运营平台企业与托运人的补贴退出力度需要加大,便于快速演化至稳定策略。 3.3.2 不同货物品类:货值p与单位时间价值β 在数组1、数组2中选定的货物类型为电子产品,但实际运输中存在多种货物品类,总结现有研究[13,18],在数组1,数组2其他参数基础上改变货物品类。对应的货值与货物时间价值取值见表3。 表3 不同货物品类时间价值取值 对不同货类下的数组1进行仿真,仿真结果见图9(a),为探究不同货类在运营平台企业与托运人形成的子系统中的演化规律,截取演化系统的z-y平面,见图9(b)。 在数组1即情形2下,货物品类为低价值低时间敏感度的工业配件时,系统到达演化稳定策略的速度更快;且在企业与托运人形成的子系统中,如图9(b)所示,货物品类是工业配件的托运人策略演化速度略高于其他货物品类,运营平台企业承接电子产品类货物的演化速度略高于其他货物品类。结果表示,在如今海运延误严重的情况下,工业配件等低价值低时间敏感度的货主开始倾向于选择中欧班列托运,但运营平台企业更倾向于运送电子产品类高价值高时间敏感度货物;总系统的演化结果说明相比于电子产品,单一的按箱补贴的补贴方式以及数组1中40%的补贴退出率对工业配件等低价值低时间敏感度货物更有利,故针对不同货物品类实行差异化补贴退出策略,可以促进系统整体稳定与市场化发展。 对不同货类下的数组2进行仿真,仿真结果见图10(a),由于运营平台企业与托运人的策略y、z很快演化完成,为探究演化稳定策略X8(1,1,1)附近的演化路径,聚焦于x随时间的变化规律x-t见图10(b)。同时,截取策略空间平面z-y,探究不同货物品类对子系统演化影响,见图11。 图10 情形6的数组2下不同货物品类对系统演化结果的影响 在数组2即情形6下,货物品类为电子产品等高价值高时间敏感度货物时,系统的演化路径相较于其他货物到达演化稳定策略X8(1,1,1)的速度更快。在情形6的企业与托运人子系统中,见图11,货物品类是工业配件以及快消时装的托运人策略演化速度略高于其他货物品类,企业办理电子产品以及家居用品的策略演化速度略高于其他货物品类。结果表明,运营平台企业更倾向于办理电子产品与家居用品等高价值货物,但由于政府补贴的持续存在,海运的延误时间过长,托运人倾向于托运快消时装、工业配件等低价值货物。但中欧班列运营总系统中,运输电子产品等高价值高时间敏感度货物更易演化至稳定策略,更适应中欧班列运营市场的发展现状。 3.3.3 政府监察率γ 为探究情形2下政府监察率γ对系统演化结果的影响,在数组1其他参数一定的条件下,令参数取值分别为γ=0.25、γ=0.35、γ=0.45、γ=0.46、γ=0.47,仿真结果见图12。 图12 情形2的数组1下政府监察率对系统演化结果的影响 由图12可知,当γ>0.46时,系统失效,与情形2的演化状态不符,表明过高的政府监察率会导致中欧班列运营系统失去市场活力,退出补贴困难。同时可以看出,随着γ的增大,系统演化至稳定策略X3(0,1,1)的速度降低,表明在三方演化博弈系统中需要保持较低的地方政府监察率,从而实现政府完全不补贴的理想化市场状态。 为探究情形6下政府监察率γ对系统演化结果的影响,在数组2其他参数一定的条件下,令参数取值分别为γ=0.43、γ=0.44、γ=0.45、γ=0.46、γ=0.49,仿真结果见图13。 图13 情形6的数组2下政府监察率对系统演化结果的影响 由图13可知,当0.43<γ<0.5时,中欧班列运营系统演化至X8(1,1,1),超出该范围,系统演化方向与情形6不符。在该监察率范围内,随着γ的增大,系统演化至稳定策略的速度提升,表明若不进行骗补惩罚,则需要在可行范围内,部分地方政府保持一定的监察力度,使混乱的补贴市场较快发展到稳定有序。 本文考虑中欧班列补贴退出与货物时间价值,建立地方政府、运营平台企业、托运人三方演化博弈模型,通过调研真实数据,将理论分析与动态仿真结合,总结和验证三方博弈主体间行为决策过程中的演化稳定均衡特性,得出以下结论: 1)中欧班列运营市场演化系统中,市场的响应速度快于地方政府的政策演变速度。对比两种典型情形2、6的演化结果,未来运营市场彻底演化至完全市场化的无补贴状态,需要地方政府采取骗补惩罚措施:若平台企业存在空载但领取补贴的行为,地方政府收回补贴并处以惩罚金大于2.6倍实际补贴金额;同时需要保持对企业与托运人的补贴退出速度基本一致。 2)当具有骗补惩罚时,补贴退出率对平台企业与托运人的策略选择影响较大,随着补贴退出率的降低,企业与托运人的策略演化速度越快,故对平台企业与托运人的补贴退出率保持一致为40%相对更适宜。在没有骗补惩罚时,补贴退出速率对整体系统的影响较大,当补贴退出率减小,系统演化至稳定策略的速度增加,故对平台企业与托运人的补贴退出率分别为30%与10%相对更适宜。综合两种情形,地方政府都应保持较大的补贴退出力度,以保证中欧班列运营市场快速演化至稳定状态。 3)单一按箱补贴的方式以及40%的补贴退出率对低价值低时间敏感度类货物更有利;在海运延误严重的大环境影响下,托运人开始倾向于选择中欧班列托运工业配件与快消时装类货物,运营平台企业倾向于运输电子产品类货物;但在持续补贴的中欧班列运营现状下,当平台企业与托运人的补贴退出率分别为30%与10%时,运输电子产品等高价值高时间敏感度货物更适应中欧班列市场。故地方政府应该实行差异化补贴退出策略,运营平台企业应该逐步拓宽市场,在不同的补贴退出节点发展适运货类;托运人也应该紧跟补贴退出速度,在恰当补贴退出节点选择中欧班列,减少托运成本。 4)政府监察率对整体系统的影响较大。具有骗补惩罚时,在三方演化博弈系统中需要保持较低的地方政府监察率,从而实现政府完全不补贴的理想化市场状态;在没有骗补惩罚时,政府监察率的可行范围为0.43<γ<0.5,监察率增大会提升系统演化速度,所以若不进行骗补惩罚时,需要在监察率可行范围内,部分地方政府保持一定的监察力度,使混乱的补贴市场较快发展到稳定有序。 本文考虑补贴退出与货物时间价值,立足于亚欧运输的现实状态,揭示了补贴退出率、货物时间价值、政府监察率等多个因素下的博弈主体策略选择机制,为中欧班列运营市场中地方政府、运营平台公司以及托运人提供了决策依据。3.3 灵敏度分析




4 结论

