ARIMA 模型在基层血站单采血小板临床需求量预测中的可行性分析

吕艺通 刘志泉 莫巧频 王东 谢庆欢 刘曼丽

近年来, 随着医疗卫生的改革, 顺德地区多家三甲、二甲医院由国内知名医科大学托管, 医院诊疗水平显著提升, 临床用血量也逐年上升。顺德区中心血站作为辖区内唯一的采供血机构, 承担着全区的采供血任务, 年采供血量达13 吨。作为一个基层中心血站, 其辖区面积、常住人口数量、人力物力的投入以及对血液应急调配的权限和灵活度都不如市级中心血站及血液中心。因此, 如何精准把控血液库存, 既要满足临床的用血需求, 又要避免因血液库存过高而过期报废, 是基层血站库存管理工作需要考虑的重要问题之一。血小板作为挽救患者的重要血液成分, 被广泛应用于血小板数量减少或功能障碍等引起的出血患者的输血治疗［1］。因其采集方式特殊, 保存时间特别短,保存期仅为5 d, 不宜大量贮存, 采供矛盾最为突出, 所以对如何科学合理地规划库存提出了更高的要求, 是一个值得深入研究的课题。ARIMA 模型是一种被广泛应用的数学模型, 通过分析时间序列前后数据的相关性, 利用历史数据的规律预测疾病发生的趋势［2］。本研究拟运用ARIMA 模型对顺德区中心血站2012 年1 月～2022 年6 月的单采血小板临床使用量进行分析并建立模型, 并用于预测2022 年7 月～2023 年3 月临床单采血小板需求量, 为顺德区中心血站单采血小板的招募采集、制定合理的血小板库存提供科学依据,现报告如下。

1 材料与方法

1.1 数据来源 通过SHINOW9.5 现代血站管理信息系统, 获取顺德区中心血站2012 年1 月～2022 年6 月的单采血小板使用量数据(因本研究时间段内, 顺德区中心血站所制备的浓缩血小板量极少, 所以不纳入本次研究对象)。临床单采血小板使用量以治疗量计算［3］,1 个治疗量血小板计数≥2.5×1011/L。

1.2 建立ARIMA 模型 建立ARIMA 模型的步骤：①原始时间序列及平稳化处理。绘制2012 年1 月～2022 年6 月顺德区中心站单采血小板临床使用量的原始时间序列图, 分析原始序列图是否为具有趋势和季节性趋势的不平稳序列, 对不平稳序列进行差分, 使序列平稳化。②ARIMA 模型识别和参数估计。根据ACF 图和PACF 图的特征, 以及是否出现拖尾或截尾的情况来推断出p、d、q 值, 并初步建立若干个备选的ARIMA 模型, 如果时间序列有明显的趋势和季节性趋势, 应选择建立ARIMA(p, d, q)(P, D, Q)s 乘积季节性模型, 其中p、q 分别为非季节自回归和移动平均的阶数, P、Q 分别为季节性自回归和移动平均的阶数, d、D 分别为差分和季节性差分的次数, s 为循环的季节周期［4］。对备选模型参数P 值进行检验, 若P＜0.05, 则差异有统计学意义, 参数检验通过。根据时间序列的识别规则, 结合ACF 图、PACF 图和贝叶斯准则(BIC准则), 对各个模型的标准化BIC 值的大小进行比较,BIC 值越小的模型, 拟合效果越好［5,6］, 从而选出最优模型。③ARIMA 模型检验。根据残差序列的自相关图、偏相关图和残差序列Ljung-Box Q 的统计结果判断残差是否存在自相关性, 若P＞0.05, 则残差通过白噪声显著性检验, 所建模型拟合效果较好。④模型预测。利用建立的最优模型, 预测2022 年7 月～2023 年3 月顺德区临床单采血小板的使用量, 并与实际使用量进行比较, 计算平均相对误差, 以验证模型的拟合效果。

1.3 统计学方法 应用SPSS23.0 统计学软件对单采血小板临床使用量进行数据录入, 并对数据进行统计分析, 建立ARIMA 模型。对确立的模型进行白噪声检验, P＜0.05 为差异有统计学意义。

2 结果

2.1 原始时间序列分析及平稳化处理 通过绘制顺德区中心血站2012 年1 月～2022 年6 月单采血小板临床使用量的原始序列图(见图1), 由原始序列图可见, 单采血小板临床使用量呈逐年上升趋势, 而且序列图存在明显的季节性周期波动, 以12 个月为1 个周期, 每年的1、2 月份单采血小板使用量最低, 每年的7、8、11、12 月份使用量最高。原始序列图不平稳, 因此,对数据进行1 阶差分和1 阶季节性差分, 差分后的序列图围绕0 值上下波动, 为平稳序列(见图2)。

图1 单采血小板临床使用量的原始序列图

2.2 模型的识别和参数估计 因2012 年1 月～2022 年6 月单采血小板临床使用量呈逐年上升趋势, 而且序列图存在明显的季节性周期波动, 所以选用ARIMA(p, d, q)(P, D, Q)s 乘积季节性模型, 由2.1 分析可知,季节性周期为12 个月, 故s=12, 对数据进行平稳化处理时, 分别进行了1 阶差分和1 阶季节性差分。因此, d=1, D=1。通过分析差分后的ACF 图(见图3)和PACF 图(见 图4)可 知, ACF 图 在 滞 后1, 2, 5, 7, 12,13 阶时均有突起, 拖尾和截尾特征不明显, 故q=0；PACF 图在滞后1, 2 阶突起, 第2 阶后明显回缩, 呈2 阶截尾, 故p=2。另外, ACF 图在滞后12 阶时显著不为0, 故Q=1；PACF 图在滞后12 阶附近显著不为0,故P=0 或1。因此, 初步识别的模型为ARIMA(2, 1, 0)(0, 1, 1)12和ARIMA(2, 1, 0)(1, 1, 1)12。对所识别的模型进行参数估计和参数检验(见表1), 由表1 可知, 模型ARIMA(2, 1, 0)(0, 1, 1)12的BIC 值 小 于 模 型ARIMA(2, 1, 0)(1, 1, 1)12的BIC 值, 且模型参数差异有统计学意义(P＜0.05), 因此, 确定模型ARIMA(2, 1, 0)(0, 1, 1)12为最优模型。

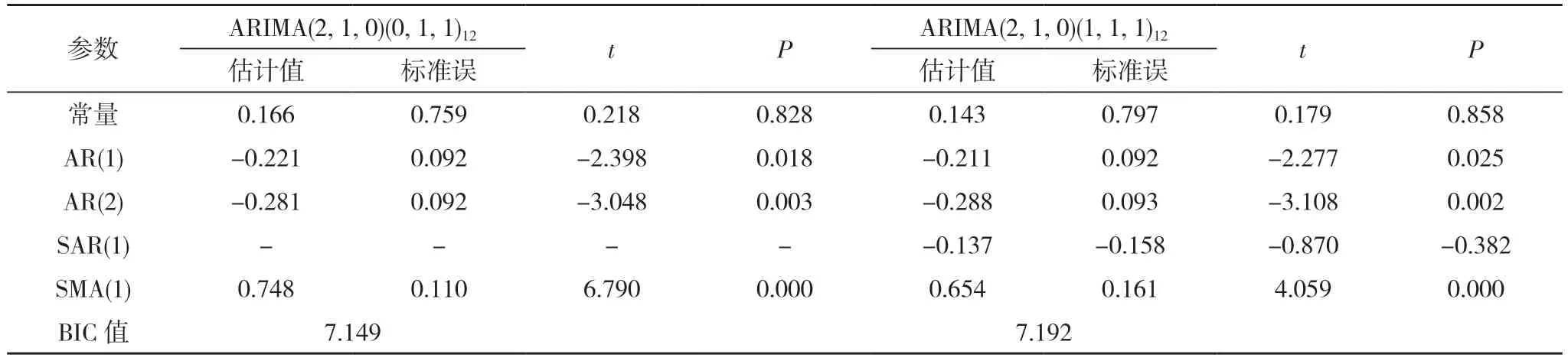
表1 单采血小板临床使用量识别模型的参数估计和参数检验

图3 单采血小板临床使用量经1 阶差分和1 阶季节差分后ACF 图

图4 单采血小板临床使用量经1 阶差分和1 阶季节差分后PACF 图

2.3 模型检验 对最优模型ARIMA(2, 1, 0)(0, 1, 1)12残差序列进行白噪声检验(见图5), 结果可见残差序列ACF 和PACF 落 在95%CI 内；Ljung-BoxQ 统 计 量 为24.941, 差异无统计学意义(P＞0.05), 说明残差是随机分布的, 残差不存在相关性, 为白噪声序列, 模型检验通过, 适合用于单采血小板使用量的预测。

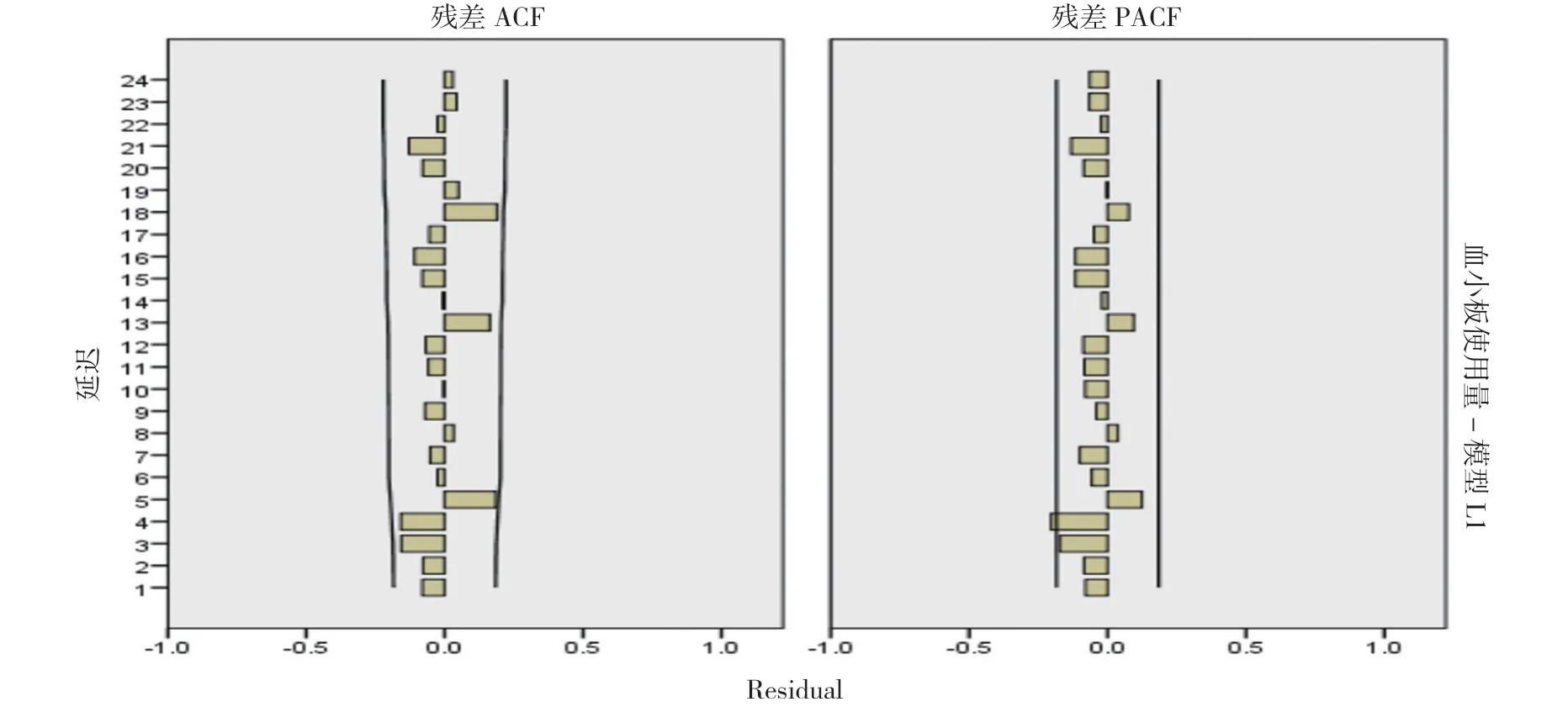
图5 模型ARIMA(2, 1, 0)(0, 1, 1)12 残差序列ACF 和PACF 图

2.4 模型预测 应用模型ARIMA(2, 1, 0)(0, 1, 1)12对顺德区2022 年7 月～2023 年3 月的单采血小板临床使用量进行预测, 预测结果与实际值均在95%CI 范围内, 平均相对误差为7.06%(见表2)。由2012 年1 月～2022 年6 月的模型拟合图可知, 预测值与实际值的曲线趋势拟合程度较高(见图6)。大量研究显示［7-9］, 平均相对误差＜10%, 则说明所建模型拟合效果较好, 精确度较高。

表2 2022 年7 月～2023 年3 月单采血小板临床实际使用量与预测量比较(治疗量)

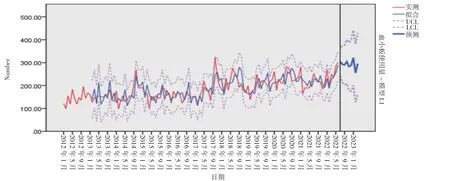
图6 单采血小板临床使用量ARIMA(2, 1, 0)(0, 1, 1)12 模型拟合效果图

3 讨论

ARIMA 模型通过对具有趋势和季节性趋势的时间序列进行建模, 对每个季节周期中同时间点的序列值进行分析, 提取季节趋势, 并对每个季节周期内部序列值的变化提取非季节性成分来做预测［10］。它充分考虑了时间序列上的依存关系和随机波动造成的干扰, 具有建模相对简单、短期预测精度较高、经济实用等优点, 目前已被广泛应用于卫生领域的病毒疫情发展趋势［11］、疾病发展情况［12,13］、临床用血趋势［14］等的预测。有研究显示［15］, ARIMA 模型在预测临床用血需求的精确性优于其他时间序列模型。

尽管目前国内已经有不少学者运用不同的数学模型对临床用血量进行预测［16,17］, 但大部分都是基于省级血液中心和市级中心血站的历史用血数据而进行的预测, 而对县、区级血站的相关研究报道甚少, 对基层血站的临床用血预测缺乏参考依据。本研究通过按月份对顺德区中心血站2012 年1 月～2022 年6 月的单采血小板使用量进行统计分析, 并运用ARIMA 时间序列模型进行建模, 经过参数检验和BIC 准则对初步确定的模型进行检验, 最终确定模型ARIMA(2, 1, 0)(0, 1, 1)12为最优模型。运用最优模型对顺德区中心血站2022 年7 月～2023 年3 月的单采血小板临床使用量进行预测, 结果显示预测值与实际值的曲线趋势基本一致, 预测结果值与实际值均在95%CI 范围内, 平均相对误差为7.06%, 说明预测效果较精确, 预测效果好。所建模型适合用于顺德区的临床血小板需求量预测。

目前, 顺德区中心血站的单采血小板供应方式有两种：①对于常规患者, 医院提前预约下单, 献血科招募采集, 检测合格后发放给临床。②对于危急患者, 医院电话向血站提出紧急用血申请, 血站评估通过后, 发放应急库存。但在实际工作中, 由于临床血小板的需求难以估计, 当血小板需求剧增时, 会导致预约的单采血小板供应延迟和应急库存贮备不足等情况的发生。通过利用ARIMA 模型提前预测每个月的血小板需求量, 献血服务科可根据预测结果, 有效规划献血者的招募和保留工作, 提高招募效率, 供血服务科可根据预测结果, 合理地制定动态的单采血小板应急库存和对临床医院采取必要的用血管理措施, 在一定程度上弥补了基层血站依靠工作经验来预测库存的不足, 有利于维持单采血小板的采供平衡, 既保证了临床用血, 也避免了血液的过期报废。但该模型也有一定局限性, 研究显示, 该模型是通过历史数据的惯性趋势而建立的,忽略了国家的重大政策调整和突发事件等外在因素,只适用于短期预测［18］。因此, 在今后的研究工作中,需要不断更新数据, 及时对模型进行修正和调整, 以提高预测结果和实际结果的拟合精确度。