港口多式联运“公转铁”的三方演化博弈研究

张 慧,周信哲,陈月艳

(1.杭州电子科技大学 管理学院,浙江 杭州 310018;2.杭州电子科技大学 信息工程学院,浙江 杭州 311305)

一、研究背景与文献综述

(一)研究背景

2020年9月,习近平在第75届联合国纪念峰会上提出“双碳”目标。次年10月,中共中央、国务院发布相关文件,指出要大力推动节能降碳,提升低碳发展水平[1]。多式联运通过综合公、水、铁等多种运输方式,调整交通运输结构,在降本增效和低碳环保等方面效果显著[2,3]。为普及推广多式联运,国务院办公厅发布《推进多式联运发展优化调整运输结构工作方案(2021—2025年)》,鼓励港口航运、铁路货运、货物运输代理及平台型企业加快向多式联运经营人转型。此后,依托国内港口码头为集疏节点的多式联运企业如雨后春笋般冒出,构建以港口水运为主的“主从”协同格局,其组织模式主要有:“铁-水联运”模式和“公-水联运”模式[4]。相较两种模式,铁路单位货物周转量的能耗和碳排放量仅为公路的1/7和1/13,政府希望大宗货物运输以“公转铁”“公转水”为突破点,改善综合性交通运输网络,“公转铁”低碳转型已成大势所趋。然而,我国现阶段两者模式选择和货运量相差悬殊,铁水联运模式展开仍旧遭受巨大阻力。这主要源于:港口多式联运企业考虑到铁水联运业务流程和数据信息不同导致的组织协同复杂,模式转变需要与新承运人沟通,定价所造成的成本投入,以及运输方式衔接配套站台设备设施不够完善等问题[5];货物托运人则更青睐于公水联运在各个物流环节的衔接灵活和提供“门到门”的个性化服务。若要解决以上问题,不能单靠港口多式联运企业或货物托运人节能降碳的自觉意识,做到政策响应、积极合作,还需要地方政府的外在激励和引导,并随着时间推移采取动态调整。因此,探究港口多式联运企业“公转铁”的作用因素具有现实意义。

(二)文献综述

作为一个新兴的研究领域,多式联运在过去的20年里获得越来越多的研究兴趣[6]。港口多式联运是指以港口作为重要枢纽,区别于单一方式运输、由两种或两种以上运输方式相互衔接的联合运输方式[7],其节能减排效果受到许多学者的关注,赵宇哲等[8]开发海运网络重建成本模型,同时设计求解算法,以降低二氧化碳排放;邓学平等[9]考虑多种不确定性,同时最小化碳排放、风险和运输成本的多目标模型,提出基于“见证”软件模拟的多模态线路参数动态计算方法来减少碳排放。港口多式联运推动交通运输结构的低碳转型,有助于实现可持续和环保的货物运输,符合全球对减少碳排放和应对气候变化的需求[10]。

目前,国内外许多学者对低碳转型的演化博弈研究主要包括博弈方的选择、博弈主体的低碳转型策略以及各博弈方的策略选择稳定性等。(1)在博弈方的选择方面,李丹丹和侯敬[11]对铁水联运的演化博弈进行定量研究目的是为铁路与水路运输企业协调发展;Hu和Dong[12]构建物流服务集成商(MC)与物流服务提供商(AC)演化博弈模型,研究航运业中MC和AC之间的合作行为如何解决航船的低效运营。后又有加入政府这一博弈方的研究[13-15],如李春发等[16]发现政府规制是促进金融机构投资企业绿色创新的必要手段,并创建地方政府、企业和金融机构三方的演化博弈;李存芳等[17]希望通过国家和地方政府的监察监管系统推动我国资源型企业绿色转型。不难发现政府制定相应的规则、制度都能强化博弈主体的低碳转型。(2)在博弈主体的低碳转型策略方面,柴瑞瑞和李纲[18]考虑把传统能源的洁净利用以及对可再生洁净能源的节能改造作为电力企业能源结构低碳化转型的策略着力点;陆菊春等[19]从多利益主体视角出发,考虑用政府的低碳消费补偿和企业研究投入低碳生产的额外技术来推动建筑企业低碳转型;王强强等[20]认为“拉闸限电”将帮助地方政府控制高耗能企业节能降耗。绿色转型策略还包括低碳生产[21,22]、节能降碳[23]、废旧电子产品回收[24]、绿色技术[25-27]等。由此可见,博弈主体一旦拥有高效可行的策略,就能加快推进主体的低碳转型。(3)在各博弈方的策略选择稳定性方面,Zhang Yi等[28]构建大众物流、大众物流平台(CLP)和托运人的三方演化模型,运用Lyapunov第一法分析纯策略组合演化稳定性;Lyapunov第一法是现代控制论中分析微分方程稳定性的基本方法,广泛应用于系统稳定性分析中[29]。现有研究大多仅局部分析了纯策略均衡点的稳定性,忽视了混合策略均衡点的分析。

综上所述,现有文献认可港口多式联运发挥的碳减效用,却未有将“公转铁”所推广的铁水联运模式纳入演化博弈的低碳转型策略,在低碳运输的演化博弈中也鲜少加入政府这一博弈方。本文在政府做出支持行为的背景下,构建地方政府、货物托运人和港口多式联运企业之间的三方演化博弈模型,利用Lyapunov第一法对复制动态系统的纯策略和混合策略均衡点,探讨分析各博弈方策略的稳定性以及各要素对低碳转型策略选择的影响,为港口多式联运“公转铁”的低碳转型之路提供结论与建议。

二、模型假设与构建

在港口多式联运企业“公转铁”的过程中,涉及到的主要利益方包括地方政府、货物托运人和港口多式联运企业。三方演化博弈中各博弈方之间的逻辑关系如图1所示。

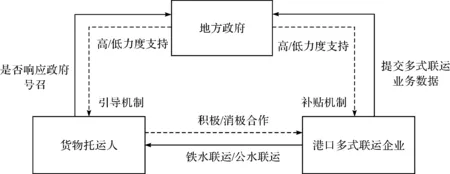
图1 三方演化博弈逻辑关系图

(一)模型假设

为建立博弈模型,并对参与者的策略、均衡点的稳定性、各因素之间的相互影响进行研究,提出以下假说:

1.地方政府面临的两种行为策略包括高力度支持和低力度支持;货物托运人面临的两种行为策略包括积极合作和消极合作;港口多式联运企业面临的两种行为策略包括选择“铁水联运”模式和“公水联运”模式。三者均是有限理性的参与方,策略选择随时间逐渐演化稳定于最优策略。

2.地方政府采用高力度支持的概率为x,则低力度支持的概率为1-x;货物托运人采用积极合作的概率为y,采用消极合作的概率为1-y;港口多式联运企业采用“铁水联运”模式运输的概率为z,采用“公水联运”模式运输的概率为1-z,x,y,z∈[0,1]。

3.地方政府为提升港口集疏运网络“公转铁”的转化率,增加社会效益,会根据合作态度和多式联运模式分别对货物托运人的引导和港口多式联运企业的补贴采取不同的支持力度。

地方政府实行高力度支持策略时,对积极合作的货物托运人提供更多的引导G1,对消极合作的货物托运人提供较多的引导G2(G1>G2);而地方政府实行低力度支持策略时,对积极合作的货物托运人提供较少的引导G3和对消极合作的货物托运人提供更少的引导G4(G3>G4),选择“铁水联运”模式合作的货物托运人才享有惠铁政策的柔性引导,并且在高力度支持和低力度支持下的两种引导差距较小。同理,地方政府实行高力度支持策略时,对“铁水联运”模式的港口多式联运企业提供补贴S1;而地方政府实行低力度支持策略时,对“铁水联运”模式的港口多式联运企业提供补贴S2(S1>S2)。

当港口多式联运企业选择“铁水联运”模式运输时会为地方政府带来社会效益,这种社会效益主要包括提升港口集疏运“公转铁”的转化率带来的减排、政绩和声誉收益。地方政府高力度支持时获取社会效益D1,低力度支持时获取社会效益D2。此外,当港口多式联运企业因选择“公水联运”模式运输的转型落后,地方政府会付出惩罚成本P。

4.货物托运人由于委托港口多式联运企业托运货物需投入的基础成本Cm,当选择“公水联运”模式时,基础成本Cmh;选择“铁水联运”模式时,基础成本Cmr(Cmh>Cmr)。同时已选择“公水联运”模式的货物托运人仍旧积极合作,说明个人配合“公转铁”的意愿更为强烈(θ为合作系数,θ∈(0,1]),后续会有概率选取“铁水联运”模式,而获得潜在收益θIe1。

5.港口多式联运企业组织多式联运过程中,需投入基础成本Cn。当选择“公水联运”模式时,基础收益Rnh(Rnh=Cmh),该模式下签署多式联运合同意味着企业必须承担公路运输安全隐患、环境代价和拥堵成本等负外部性风险可能带来的损失πRnh=πCmh,其中损失与风险成正比,π为风险系数,π∈[0,1]。基础成本Cnh,其中包含直接运输成本Cha、碳排放成本Chb。

6.当选择“铁水联运”模式时,基础收益Rnr(Rnr=Cmr),基础成本Cnr,其中包含直接运输成本Cra、碳排放成本Crb。企业业务“公转铁”低碳转型,重选承运人需付出成本Ce,但这种低碳运输模式会增加企业声誉、知名度等潜在收益Ie2。在两种多式联运模式都不出现负外部性风险且起始地、目的地和货物重量相同情况下,Chi>Cri,a,b∈i。

(二)收益矩阵构建

基于上述模型假设,得到三方博弈收益矩阵,具体如表1所示。其中,博弈三方的收益分别为π1、π2、π3。

表1 三方博弈收益矩阵

三、模型分析

(一)地方政府的期望收益及稳定性分析

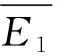
(1)

由此,可以得到地方政府的复制动态方程为:

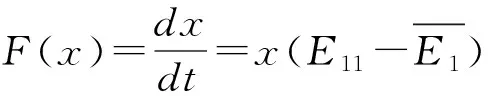
(2)

(二)货物托运人的期望收益及稳定性分析

(3)

由此,可以得到货物托运人的复制动态方程为:

(4)

(三)港口多式联运企业的期望收益及稳定性分析

(5)

由此,可以得到港口多式联运企业的复制动态方程为:

(6)

(四)三方演化博弈系统的稳定性分析

1.演化博弈均衡点求解

由地方政府、货物托运人、港口多式联运企业三方的复制动态方程式(2)、(4)、(6)可得到三维动态系统,如下所示:

设F(x)=0,F(y)=0,F(z)=0,解得复制动态方程组存在以下12个均衡点,其中包括8个纯策略解:(0,0,0)、(1,0,0)、(0,1,0)、(0,0,1)、(1,1,0)、(1,0,1)、(0,1,1)、(1,1,1);4个混合策略解(x0,y0,z0),x0,y0,z0∈[0,1]。

2.均衡点的稳定性分析

根据复制动态方程构建三方演化博弈系统的雅克比矩阵J为:

j11=(1-2x)[yz(-G1+G2+G3-G4)+z(D1-D2-G2+G4-S1+S2)];

j12=x(1-x)z(-G1+G2+G3-G4);

j13=x(1-x)[y(-G1+G2+G3-G4)+(D1-D2-G2+G4-S1+S2)];

j21=y(1-y)z(G1-G2-G3+G4);

j22=(1-2y)[xz(G1-G2-G3+G4)+z(G3-G4-θIe1)+θIe1];

j23=y(1-y)[x(G1-G2-G3+G4)+(G3-G4-θIe1)];

j31=z(1-z)(S1-S2);j32=0;

j33=(1-2z)[x(S1-S2)+S2+Cmr-Cmh-Cnr+Cnh+πCmh-Ce+Ie2]。

引用Lyapunov第一法,测试雅克比矩阵中均衡点的稳定性。当雅克比矩阵的全部特征值都为负实部,那么该均衡点就是渐进稳定点(ESS);当雅克比矩阵的全部特征值,其中有一个含有正实部,那么该均衡点就是不稳定点;当雅克比矩阵全部特征值将实部为零的除外,其余特征值都含有负实部,那么该均衡点的稳定性暂时无法确定。求得动态系统各均衡点的特征值,如表2所示。

纯策略均衡点(0,0,0)、(1,0,0)、(0,1,0)、(1,1,0)和4个混合策略均衡点均有特征值λi≥0,实部为零,则所列均衡点都不是渐进稳定点,在均衡点的演化稳定策略中以上8个均衡点不再展现。

推论1：已知G3>G4,G4-G3<0。当D1-D2-G1+G3-S1+S2<0,-(S2+Cmr-Cmh-Cnr+Cnh+πCmh-Ce+Ie2)<0时,复制动态系统仅存在渐进稳定点(0,1,1),即策略组合(低力度支持,积极合作,铁水联运)为该系统经过演化后唯一的稳定策略。

推论1表明：如表3所示,此时系统渐进稳定点是(0,1,1),而其余均衡点特征值的都至少有一个正实部,都为不稳定点。从D1-D2G4可知,当货物托运人对地方政府引导认可较大时,即使地方政府对铁路货运柔性引导力度较小,其最终也会积极与港口多式联运企业加深合作程度,配合业务转变;从S2+(Cmr-Cnr)-Ce+Ie2>(Cmh-Cnh)-πCmh可知,不同情境下,当运输风险π过大,极有可能导致企业损失报价部分损失;或者企业因低碳转型收获较大的知名度,都会增加潜在客户,激发潜在收益。从收益角度分析,前者模式收益大于后者,企业改用“铁水联运”模式。

表3 均衡点的演化稳定策略

推论2：当D2-D1+G1-G3+S1-S2<0,-(S1+Cmr-Cmh-Cn+Cnh+πCmh-Ce+Ie2)<0时,复制动态系统仅存在渐进稳定点(1,1,1),即策略组合(高力度支持,积极合作,铁水联运)为该系统经过演化后唯一的稳定策略。

推论2表明：如表3所示,此时系统渐进稳定点是(1,1,1),而其余均衡点特征值的都至少有一个正实部,都为不稳定点。从D1-D2>G1-G3+S1-S2可知地方政府发现采取高、低力度支持获得的社会效益差值大于其投入引导、补贴的成本差值时,其乐于对另两方演化方采取高力度支持策略;从G1>G2可知,当货物托运人积极合作的引导更大时,“铁水联运”模式对货物托运人的更有吸引力;从S1+(Cmr-Cnr)-Ce+Ie2>(Cmh-Cnh)-πCmh可知,在该情境下,地方政府的高力度补贴会极大地增加“公转铁”带来的收益;或者企业与铁路承运人顺畅对接,投入的转型成本较小。从收益角度分析,两种多式联运模式相比,前者收益大于后者,企业亦会选择“铁水联运”模式。

四、仿真分析

为验证演化稳定性分析的有效性,并探究相关因素的参数变动对各方策略行为的作用,在模型中赋以根据面板数据计算得来的真实数据,运用Matlab2020a开展数值仿真。

(一)均衡点检验仿真

通过参考相关文献[30]和查阅碳K线网站,得出不同联运模式下,运行基价(￥/km.t)分别为0.29/0.20,单位碳排放量(t/t.km)分别为4.2*10-5/2.7*10-5,碳交易价格(￥/t)为323。通常情况下,港口多式联运企业业务的利润率是10%-30%[31],现取不同联运方式的利润率在25%。可得港口多式联运企业“公水联运”模式和“铁水联运”模式的成本Cni、直接运输成本Cia、碳排放成本Cib、收益Cmi和利润Cmi-Cni且r,h∈i的固定参数取值,而S、G、D等其余收益、成本参数都选择文献[32-34]中摘取政府补贴、引导、社会效益等真实数据,并加以调整。

数组1、2符合推论1、2中的所有条件,其仿真参数赋值为数组1、2:G1=60,G2=55,G3=40,G4=35,S1=60,S2=40,Cmr-Cnr=53-40=13,Ie1=15,Ie2=8,Ce=5,θ=0.9,π=0.1,但数组1的D1=150,D2=120;数组2的D1=180,D2=100。

仿真结果表明,符合所有条件后,仿真结果得(0,1,1)为渐进稳定均衡点,系统此时仅存在一个演化稳定策略组合(低力度支持,积极合作,铁水联运)与推论1结论一致;在满足条件下,仿真结果得(1,1,1)为渐进稳定均衡点,此时系统仅存在(高力度支持,积极合作,铁水联运)策略组合与推论2结论一致。以上两个模型计算结果都可验证模型切实有效。

(二)参数敏感性分析

在数组2的基础上,符合推论2中的所有条件,于Matlab2020a设置博弈三方的策略选择概率(x,y,z)的初始值为(0.2,0.2,0.2),三方策略最终到达ESS点(1,1,1),即无论参数如何变化,博弈三方演化最终都会达到均衡。剖析S1-S2、G1-G3、π、Ce、Cib这些参数变化对演化博弈过程和结果的作用。其中,S1-S2和G1-G3的参数变化都与博弈双方的收益或成本直接挂钩,而π、Ce、Cib仅与博弈一方的收益或成本直接挂钩,间接影响博弈的另两方。

1.博弈双方挂钩参数的敏感性分析

(1)地方政府高、低力度支持下对港口多式联运企业补贴差值(S1-S2)的敏感性分析

为分析S1、S2不同取值变化对演化博弈过程和(高力度支持,铁水联运)结果的作用,将S1、S2分别赋以60、40,70、30,70、20,复制动态方程组在时间推移下,图2a显示其演化50次的仿真结果。

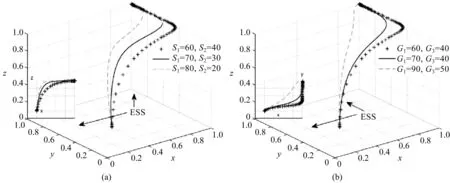
图2 博弈双方挂钩参数的敏感性分析

图2a表明,在系统演化至稳定点的过程中,随着S1-S2增加,政府发现高力度支持所负担的财政补贴远高于低力度支持时,会减缓政府采取高力度支持策略的演化速度,其选择概率也会下降。但企业能得到实质性补贴,其选择“铁水联运”模式的概率会上升。如果政府希望加快企业“公转铁”效率,就需要增加补贴力度。在实施低碳补贴措施时,政府也应当综合自身财政状况,适当调整补贴机制,保证其常态化运行。

(2)地方政府高、低力度支持下对积极合作货物托运人引导差值(G1-G3)的敏感性分析

为分析G1、G3不同取值变化对演化博弈过程和(高力度支持,积极合作)策略组合结果的作用,将G1、G3分别赋以60、40,70、40,90、50,复制动态方程组在时间推移下,图2b显示其演化50次的仿真结果。

图2b表明,在演化过程中,随着G1-G3增大,政府发现对积极合作的货物托运人,高力度支持与低力度支持之间引导的差额较大时,选择高力度支持策略的概率下降,但货物托运人能享受铁路服务质量提升、运价下浮,运输效率上升等红利,其选择“铁水联运”模式的概率会上升。相较于图2a的演化曲线可发现,有积极合作倾向的货物托运人在长期演变的过程中,即使最终做出积极合作的决定,但图2b曲线爬升至积极合作策略概率Y=1较为缓慢。这表明,在现实双方博弈中,货物托运人可能对政府的引导政策持有谨慎态度,需要通过长期观察企业“公转铁”的运输效果,以逐渐建立政策信任。

2.博弈单方挂钩参数的敏感性分析

(1)“公水联运”模式风险系数(π)的敏感性分析

满足推论2中的条件,将π分别赋以0.1,0.3,0.5,从图3-1会发现π的不同取值变化,博弈三方的策略组合依旧趋于(高力度支持,积极合作,铁水联运),但演化博弈过程中各策略选择概率(X,Y,Z)的演化曲线会产生波动,复制动态方程组在时间推移下,图3-1(a,b,c)显示其演化50次的仿真结果。

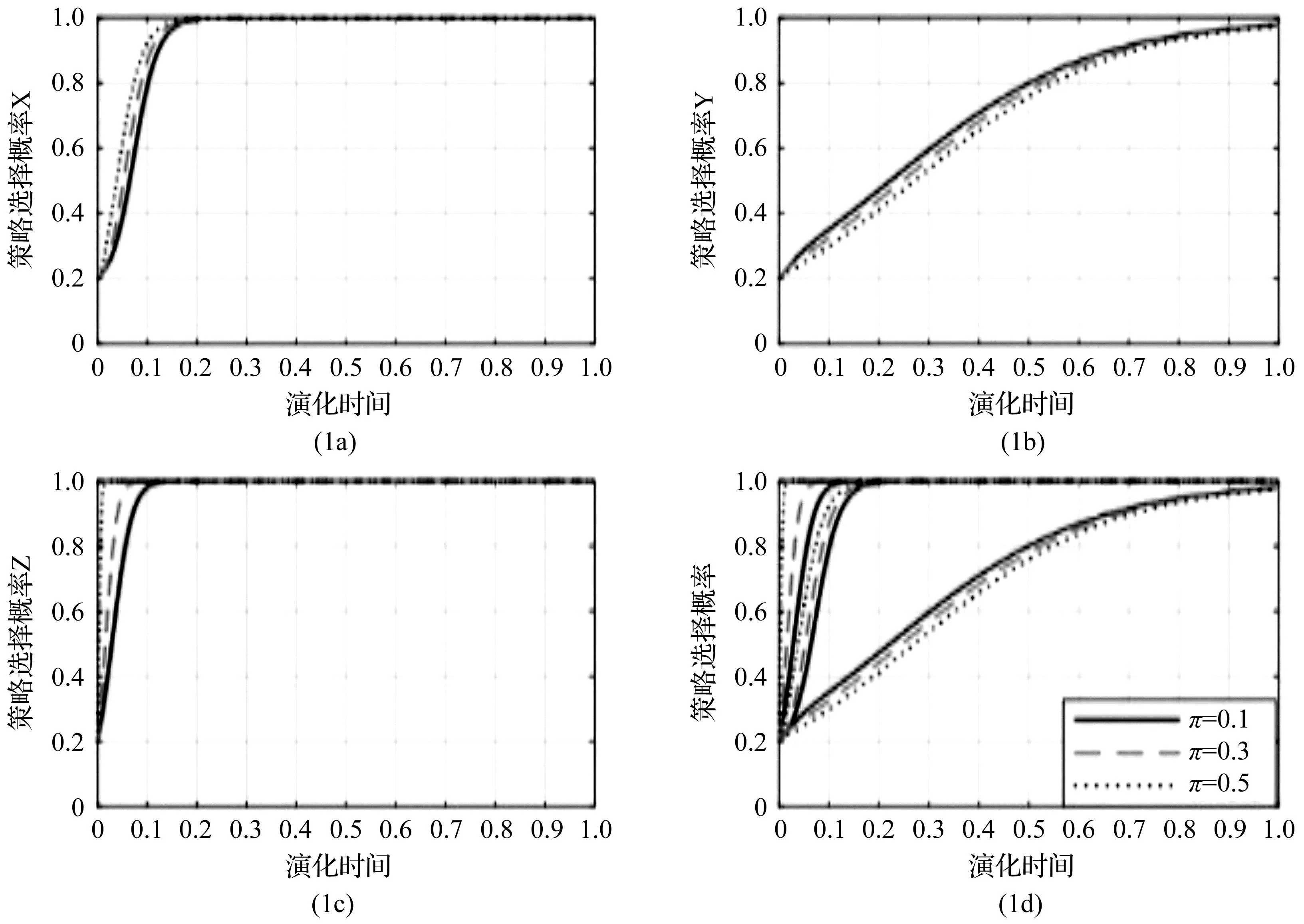
公路运输所处环境复杂,安全风险较多。当“公水联运”模式在运输途中风险系数π越高,相同演化时间下,地方政府高力度支持策略的概率会上升,面对这种情况,政府会采取加快推动铁路入港口、物流园区和大型矿企,推动大宗及中长途货物运输向铁路转移等措施,以应对公路日益复杂的运输环境和安全风险;货物托运人积极合作的概率反而下降,观察图3-1b的三条曲线,发现曲线之间较为接近,且以一种均速到达积极合作策略概率Y=1。合理推测是货物托运人作为甲方与企业签订多式联运合同,按照相关法律规定,多式联运经营人要对货物损毁进行赔偿,致使货物托运人对运输方式的风险系数并不敏感;企业对风险系数π更为敏感,图3-1c中取值π=0.5,演化曲线几乎在演化时间=0时,企业即刻选择“铁水联运”模式,而且图3-1c的演化曲线也比图3-1a反应速度更快,侧面证明企业作为市场化运营的博弈主体,对运输决策存在的风险最为敏感。

(2)港口多式联运企业重选承运人成本(Ce)的敏感性分析

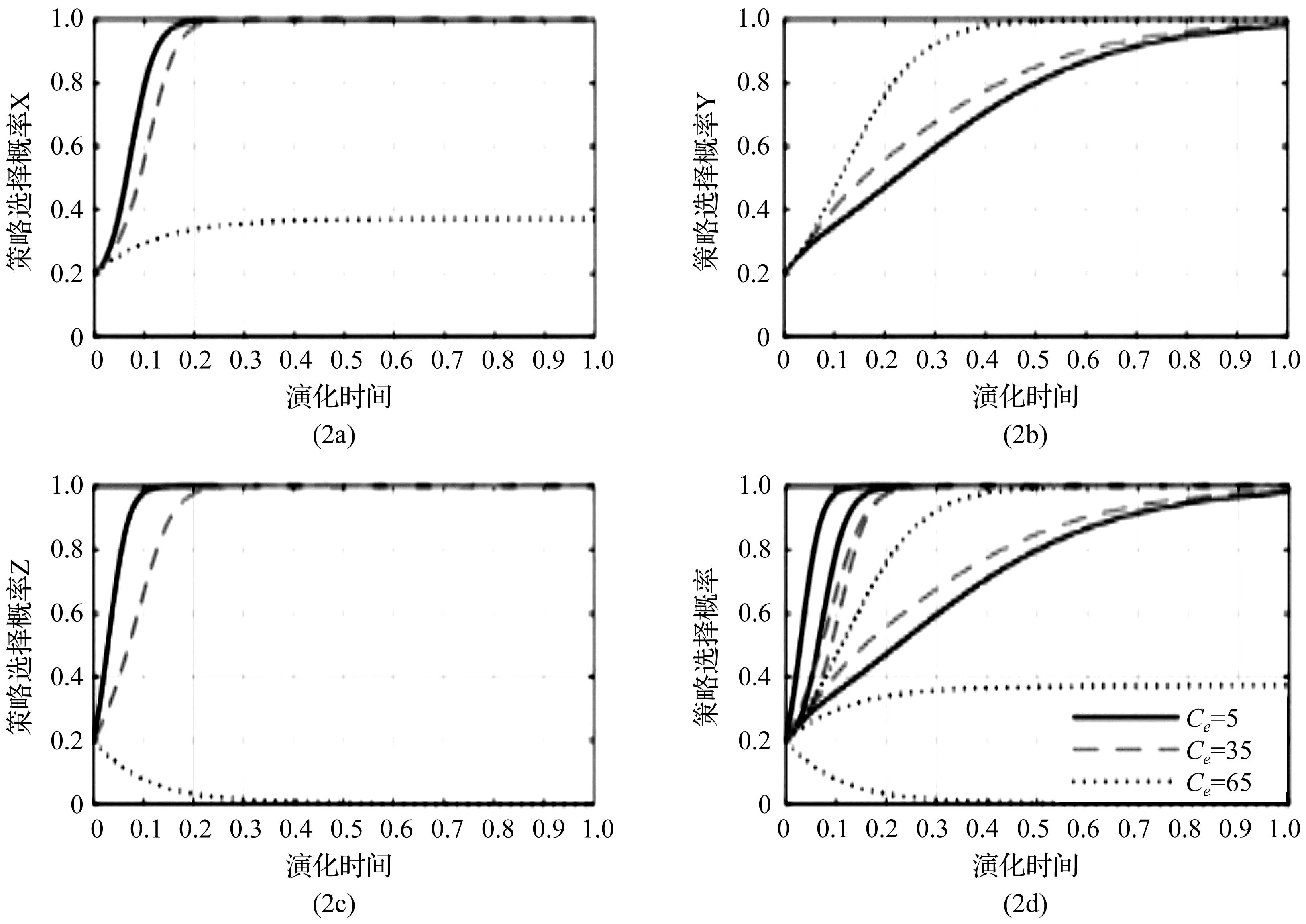
为分析Ce的不同取值变化对演化博弈过程和结果的作用,将Ce分别赋以5,35,65,从图3-2d会发现其中设置的特殊参数取值Ce=65,不满足推论2中的条件,会使系统稳定均衡点从(1,1,1)转变为(0.4,1,0),博弈三方的策略组合(高力度支持,积极合作,铁水联运)同时发生变动。图3-2呈现复制动态方程组在时间推移下,演化50次的仿真结果。

重选承运人成本Ce的存在,一定程度上会对“公转铁”效率造成阻碍。随着成本Ce越高,相同演化时间下,地方政府高力度支持策略概率会下降,在图3-2a中Ce=65的线条显示策略选择X≤0.4,这表明Ce虽是企业期望收益中的成本支出,但成本过高也会间接导致政府决策的不确定性;货物托运人即使在图3-2b中Ce=65时,积极合作策略概率最终也会是Y=1,但演化时间t∈[0,0.2]这段曲线中政府高力度支持策略的概率快速上升,显然货物托运人不愿面对因Ce过高,企业停止“公转铁”低碳转型,取消“铁水联运”模式的可能性;港口多式联运企业由于Ce过高,突破企业的心理阈值,策略选择仍旧保持“公水联运”模式。例如,铁路承运人资源紧张、铁路运价高昂或合作难度大等问题都会导致企业错失与铁路承运人建立新合作伙伴关系的机会。

(3)两种联运模式产生的碳排放成本差值(Chb-Crb)的敏感性分析

以Chb-Crb的差值变化来分析碳排放成本Cib对演化博弈过程和博弈三方的策略组合(高力度支持,积极合作,铁水联运)结果的作用,将两种模式下的Crb和Chb分别赋以5、10,10、20,15、30,复制动态方程组在时间推移下,图3-3显示其演化50次的仿真结果。

在全国碳市场中,碳排放配额交易价格作为市场的风向标,实时反映市场的供给与需求,碳交易市场成交价格γ随时间变化呈现无规律波动的趋势。已知单位的碳排放量β,“公水联运”模式远高于“铁水联运”模式,并且起始地、目的地和货物重量相同情况下,Crb

随着Chb-Crb的差值增加,相同演化时间下,博弈三方的策略组合(高力度支持,积极合作,铁水联运)的概率都呈现上升趋势,政府和企业的策略概率X,Z=1时,演化时间分别是ta=0.2,tc=0.1,证明两方在“公转铁”演化前期就对参数Cib极为重视,积极响应国家“双碳”理念。故而,Chb-Crb差值越大,政府采取高力度支持加快联运模式“公转铁”低碳转型,企业则更为倾向碳排放成本较少的“铁水联运”模式。

五、结论与建议

本文综合考虑了影响港口多式联运企业“公转铁”低碳转型的因素,构建地方政府、货物托运人和港口多式联运企业三方演化博弈模型。通过求解均衡点、分析均衡点稳定性和参数敏感性后,研究结论如下:(1)地方政府制定支持力度的高低取决于其所能回报的社会效益与投入的引导、补贴成本之间的差值大小;(2)地方政府支持力度的高低不干扰货物托运人和港口多式联运企业“公转铁”的选择结果,但可以加速另两方的策略选择理想化。该研究结论与政府采取支持、补贴或奖惩措施加速策略选择的结论[15,22,35]相一致;(3)货物托运人对待“公转铁”存在先天意愿偏好,策略选择会随着演化时间的推移,均速地趋向积极合作;(4)港口多式联运企业作为博弈三方的核心,随着影响因素变化,其演化时间缩短且波动最为剧烈。该研究结论与核心企业在博弈系统演化中相较其他主体变动幅度最大[24]的结论相符。公路运输风险上升、企业重选承运人成本下降或碳排放成本升高都会拉动企业“铁水联运”的市场需求。研究肯定了地方政府支持在推动联运模式“公转铁”中发挥的效用,并丰富了以“公转铁”作为港口多式联运企业低碳转型路径的演化博弈研究。

基于上述研究结论,从博弈三方各自利益角度为推动“公转铁”提出对策建议:(1)地方政府盲目地高力度支持,可能陷入财政入不敷出、社会效益回报低下的两难窘境。为防止上述状况出现,一方面,政府需要全面考虑自身财政和受益企业增量规模等内外因素,动态调整引导、补贴机制,避免过度依赖政策扶持。另一方面,科学分析和预测公、铁两种运输方式的市场供需,避免两者的市场规模失衡,致使回报政府的社会效益降低。(2)货物托运人已经意识到未来港口集疏运的运输结构将向铁路端倾斜,但受惯性思维和政策走向不明干扰,大部分时间处于摇摆阶段。为吸引托运人货源从公路转向铁路,政府引导应从两个方面下手。一方面,通过扩充货物品类和空间、创新物流服务、下浮铁路运价等有利举措,让托运人看到具体效益,满足实际需求。另一方面,将宣传重点放在“公转铁”的长远作用和战略地位,让托运人知晓运输结构供给侧改革是未来交通运输发展的必由之路。(3)港口多式联运企业需从法律层面警惕公路风险逐年递增带来的巨大赔偿隐患;政府通过合理手段调控企业碳配额、碳核查力度或者碳排放超支惩罚等,碳排放成本一定程度地升高,反而能倒逼企业“公转铁”;重选承运人成本过高,可以视作企业与新的铁路承运人达成合作伙伴关系的协商中,出现铁路运营商资源缺乏、信息沟通不畅等阻碍,为使企业对“铁水联运”模式恢复信心,维持运输服务多样性。政府也应增设公共信息平台,辅助企业寻找合适承运人,并且完成托运人、承运商、多式联运企业之间的信息共享,打造高效、无缝对接机制。

本文也存在一定的局限性:(1)本文对模拟仿真中各参数赋以真实数据,但除多式联运企业运输成本数据外,其余数据大多是直取文献中的变量数据,加以推测赋值,未避免主观性偏误,仍不够准确。(2)本研究分析仅侧重于在演化条件成立后,成本与收益参数对三方博弈中各主体是否产生影响、敏感性如何,并没有思考临界状态下让演化条件成立所付出的转换代价。下一步可在三方演化博弈模型中引入海关、铁路局等参与者,构建多主体的动态、重复博弈模型,使其更符合现实。