补贴政策对平台赋能供应链协同的影响研究
杜伟锦,范婷婷,2,杨 伟
(1.杭州电子科技大学 管理学院,浙江 杭州 310018;2.景德镇艺术职业大学,江西 景德镇 333000)
以工业互联网为代表的第四次工业革命正在全球范围内兴起,抓住并利用好此次工业革命机会,有助于中国制造业实现新旧动能转换,推动工业经济高质量发展。工业互联网平台为供应链企业提供汇聚供需信息和优化增值的资源供需服务,在现实中已涌现出不少典型事例。例如,海尔卡奥斯和树根互联等工业互联网平台分别打造了汇聚或优化资源供需的专属服务版块以实现赋能供应链协同。工业互联网平台作为一种新兴事物,众多企业对其功能和效果还存在“不敢用”或者因成本费用等“用不起”的疑虑,从而导致目前平台应用落地实践推进缓慢[1]。当前,中国各地政府推出一系列激励政策,但工业互联网平台赋能供应链协同的市场效应并没有得到广泛认可和推广,主要原因在于当前政策缺乏科学有效的引导以及有效供给对需求不能及时响应[2-4]。因此,研究政府不同补贴政策对实现工业互联网平台赋能供应链上下游企业协同发展的影响,对促进政府制定合适的补贴机制,实现补贴政策增强工业互联网平台赋能供应链协同的市场效应具有重要的意义。
工业互联网平台能够为制造企业联通海量生产要素,促进供应链整体协调以及资源供需决策协同,提高供应链整体效益[5-7]。当前有关政府政策对工业互联网平台影响的研究中,郑勇华等[8]分析了平台赋能制造业数字化转型的作用机理,并研究了政府的补贴政策对推动平台发展和引导工业企业参与平台服务的影响。周晓阳等[9-10]发现政府补贴对于制造业企业和工业互联网平台的策略在一定程度上能积极促进双方的合作。考虑到政府补贴的影响,周晓阳等[9]构建包含制造业企业、工业互联网平台和第三方开发商的三方演化博弈模型,探究平台赋能制造业企业数字化转型以及促进工业互联网持续有效发展的关键。周晓阳等[10]构建了政府、工业互联网平台和企业的三方演化博弈模型,发现采用成本分摊方式可以有效提升企业参与平台服务的积极性。基于研究工业互联网平台增值服务系数和成本节约系数等因素对博弈主体策略的影响,潘小军[11]构建三级供应链的合作博弈,提出工业互联网平台增值服务水平(质量)和成本节约系数对博弈主体的策略产生了重要影响。学者孙云飞[12]研究中国供应地区安全公共产品的选择时,将“搭便车者”和“被搭便车者”的经济行为区分为两者对于获得的收益是否支付了相应的费用。上述研究多从企业数字化转型的角度分析政策对平台赋能机制的影响,较少以资源供需为视角,区分政府补贴对象,研究不同补贴政策对工业互联网平台赋能供应链协同的影响。
针对平台现存短板、困境和理论研究不足,本文视工业互联网平台和供应链企业作为有限理性的主体,区分政府补贴对象,基于资源供需的视角,采用演化博弈研究方法,构建三方演化博弈模型,从资源供需视角,研究不同补贴政策情境中工业互联网平台赋能供应链协同的区别。本文以政府补贴为前提,将政府补贴分成补贴供应链企业和补贴工业互联网平台,分别构建博弈矩阵,进行求解与分析。首先,分析政府补贴供应链企业时,影响因素对博弈主体策略选择的影响有何变化。其次,分析政府补贴工业互联网平台方各影响因素的表现。最后,将以政府补贴背景的两种情境进行对比分析,得出研究结果。
一、三方演化博弈模型构建与解析
(一)问题描述与基本假设
本文将供应链核心制造企业的角色定位为资源需求方,将供销企业的角色定位为资源供给方。资源需求方和资源供给方作为平台赋能的对象,面对工业互联网平台的赋能服务,考虑众多影响因素,进行决策是否参与。
供应链供给端不能及时响应需求端资讯,导致资源供需效率低下,增加了供应链“断链断供”的风险。平台方从“降本”和“增效”两个方面开展赋能服务工作,提供优化服务方案和普通服务方案,以提升资源供需合作效益,促进供应链实现协同。普通服务方案是指通过汇聚资源供需信息,缩短资源供需匹配的时间,达到“降本”的服务目的。优化服务方案是通过提供轻量化工业app或者专业、有针对性的云化增值服务,增加供需方的资源匹配程度,协同决策与生产,提高生产运营过程中的效率,从“降本”和“增效”两个方面共同提升资源供需合作效益。当资源供需方均参与平台的优化服务完成资源供需合作,则实现了平台赋能供应链协同的优化模式,若是双方均参与普通服务,则实现了普通式供应链协同。基于以上分析,本文构建了由供应链核心企业、供销企业、平台组成的三方演化博弈模型。为使研究更加严谨,本文进行如下的假设:
假设1:资源供给方和需求方基于资源供需合作的基础收益分别为Rs和Rd,成本为(1+n)Cs和(1+m)Cd。平台提供普通和优化方案的服务成本分别为Cp1、Cp2。n、m∈[0,1]。
假设2:若资源供需方均参与普通服务,资源供需方分别可节约合作成本nCs、mCd。同时,向平台支付Es1、Ed1的服务费。若资源供需方均参与优化服务时,分别增加βRs和βRd的收益同时节省节约合作成本nCs、mCd。此时,资源供需方分别向平台支付(1-θ)Et、θEt的平台服务费。平台获得具有Ep的声誉收益,具有(1+β)Cp2服务成本。θ∈(0,1)。
假设3:若只有资源供给方参与平台的优化方案,以π单位的增值服务系数[11]赋能于资源供给方效益提升,此时平台收取Efs的服务费,具有(1+π)Cp2服务成本。若只有资源需求方参与时,以ω单位的增值服务系数赋能资源供给方效益提升,此时平台收取Efd的服务费,具有(1+ω)Cp2服务成本。
假设4:当资源供需方仅有一方参与优化服务时,参与的一方因平台增值服务获得供应链管理效益等提升,提高了其资源供需订单的准确性或者供需资源质量得到保证,间接给未参与优化服务的另一方带来资源供需收益的提升,即存在所谓的“搭便车”效应[12],λ、α分别表示资源供给方和资源需求方的“搭便车”效益系数。其中λ≤π;α≤ω、β>ω;β>π;β、ω、π、α、λ∈[0,1]。
假设5:当政府补贴企业时,Gs、Gd分别表示供给方、需求方参与服务获得的补贴额,S1、d1为资源供、需方参与普通方案获得的补贴力度,S2、d2分别是资源供、需方参与优化方案获得的补贴力度。若是政府补贴平台方的情境,K表示平台提供服务方案的补贴额,P1、P2分别表示针对普通方案和优化方案平台获得的补贴力度。S1、d1∈[0,1],S2、d2∈[0,1]。
三方演化博弈模型中涉及的参数符号及其含义解释如表1所示。

表1 模型参数符号意义
(二)博弈模型求解
1.政府补贴平台情境
根据模型假设和政府补贴平台情境构建如下三方演化博弈模型[13-15],如表2。

表2 政府补贴平台博弈支付矩阵
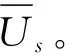
Us1=yz[(β-π)Rs-(1-θ)Et+Efs]+z(πRs-Efs+Es1)+Rs-Cs-Es1
(1)
Us2=yzλRs+Rs-(1+n)Cs
(2)
(3)
由式(1)、式(2)和式(3)计算可得资源供给方的复制动态方程,如下。
(4)
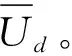
Ud1=xz[(β-ω)Rd-θEt+Efd]+z(ωRs-Efd+Ed1)+Rd-Cd-Ed1
(5)
Ud2=xzαRd+Rd-(1+m)Cd
(6)
(7)
由式(5)、(6)和(7)可求得资源需求方的复制动态方程,如下。
(8)
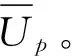
Up1=xy[Et-Efs-Efd+Ep-(β-π-ω)Cp2+x(Efs-πCp2)+y(Efd-ωCp2)-Cp2
(9)
Up2=xEs1+yEd1-Cp1
(10)
(11)
由式(9)、(10)和(11)可得工业互联网平台的复制动态方程,如下。
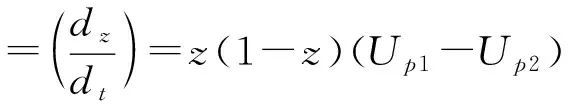
(12)
2.政府补贴供应链企业情境
根据模型假设和政府补贴企业情境构建如下三方演化博弈模型,如表3所示。

表3 政府补贴企业博弈支付矩阵
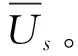
(13)
资源需求方的复制动态方程,如下。
(14)
工业互联网平台方的复制动态方程如下。
(15)
(三)三方演化博弈模型稳定性分析
1.政府补贴平台情境
根据微分方程稳定性定理,确定政府补贴企业情境中博弈主体存在的最优状态,需要计算出三维动力系统Jacobian矩阵特征值。当博弈主体策略选择组成的均衡点满足Jacobian矩阵特征值均小于0时,该均衡点是系统的演化均衡点,是博弈主体的稳定策略[16-17]。
由式(4)、式(8)和式(12)联立可得政府补贴平台的三方演化博弈系统的雅克比矩阵表达式为J1:
由雅克比矩阵计算结果可得Fx(x,y,z)、Fy(x,y,z)、Fz(x,y,z)表达式,分别令Fx(x,y,z)=0,Fy(x,y,z)=0,Fz(x,y,z)=0,可得到资源供给方、资源需求方和工业互联网平台在博弈过程中存在8个纯策略均衡点,分别为G1(0,0,0),G2(0,0,1),G3(0,1,0),G4(1,0,0),G5(0,1,1),G6(1,0,1),G7(1,1,0),G8(1,1,1),进而可求得各均衡点所对应的 Jacobian矩阵特征值,如表4。
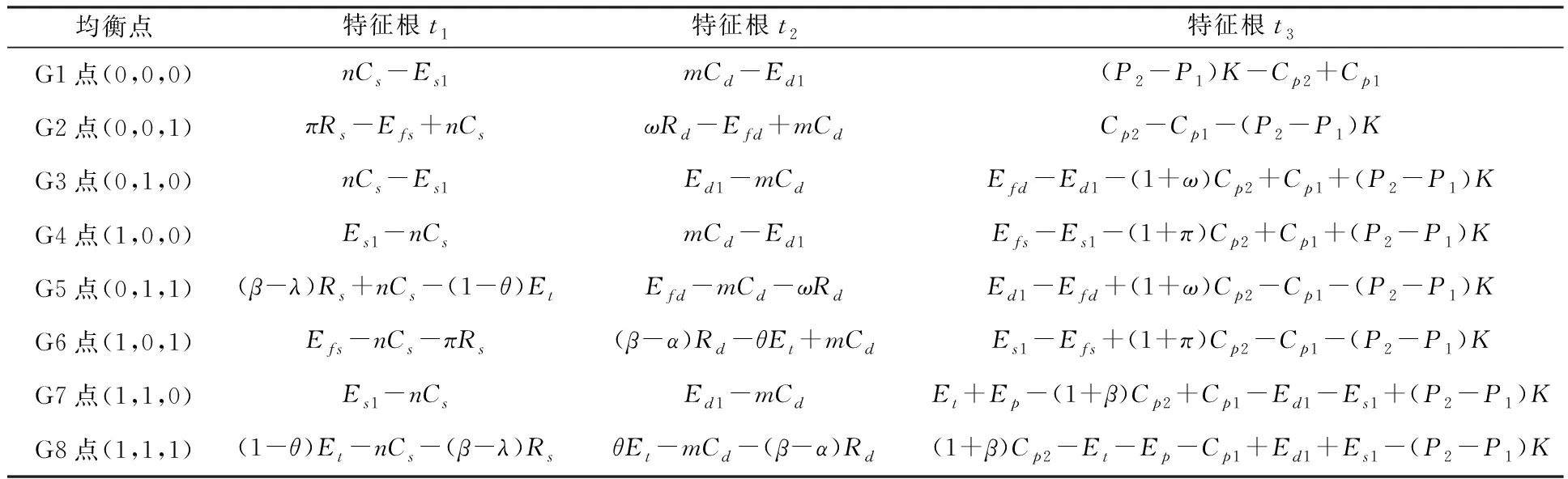
表4 各均衡点对应的Jacobian矩阵特征值
根据李雅普诺夫判别法可知,当雅克比矩阵的所有特征根符号全为负时,该均衡点是稳定点。分别对8个均衡点的三个特征值进行分析,可确定各均衡点的稳定性,以下将进行分情况讨论。
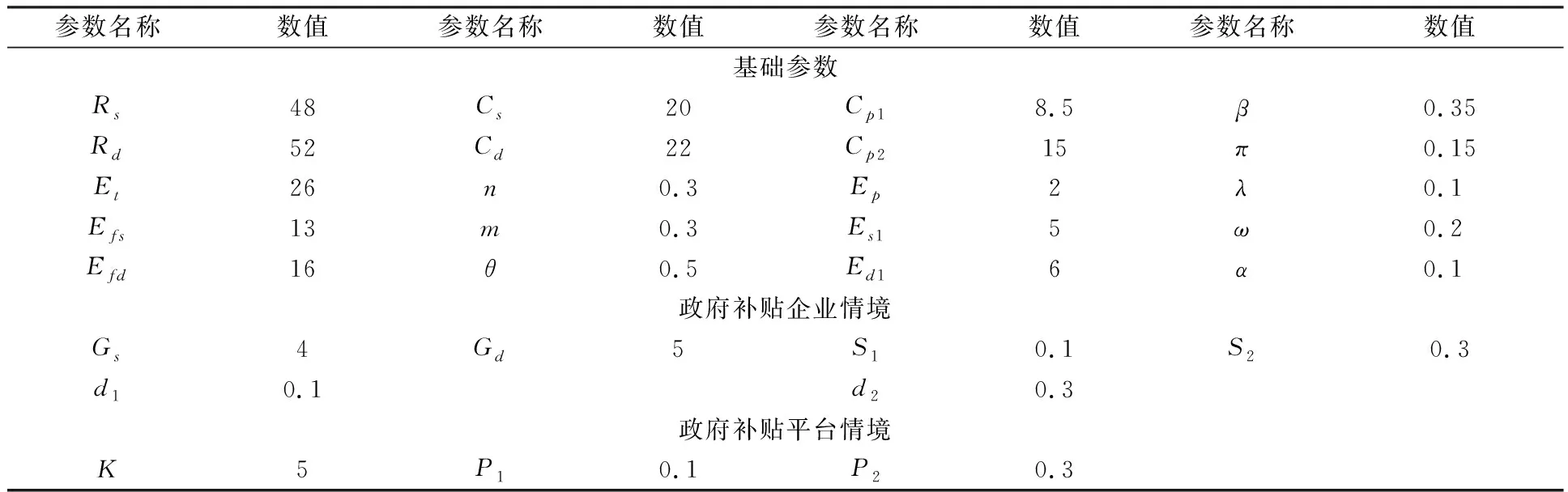
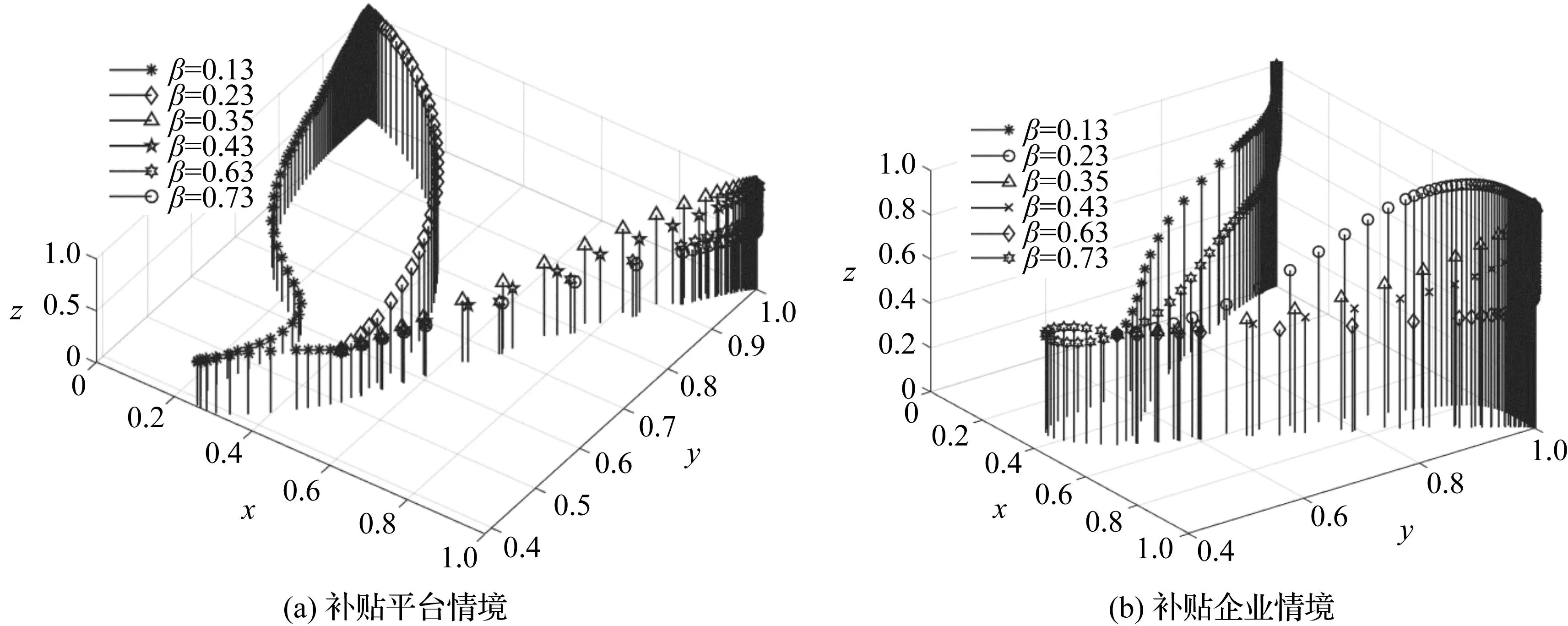
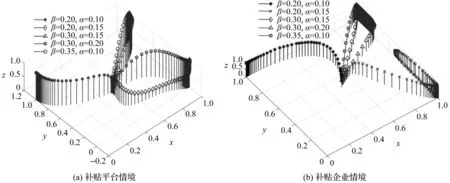
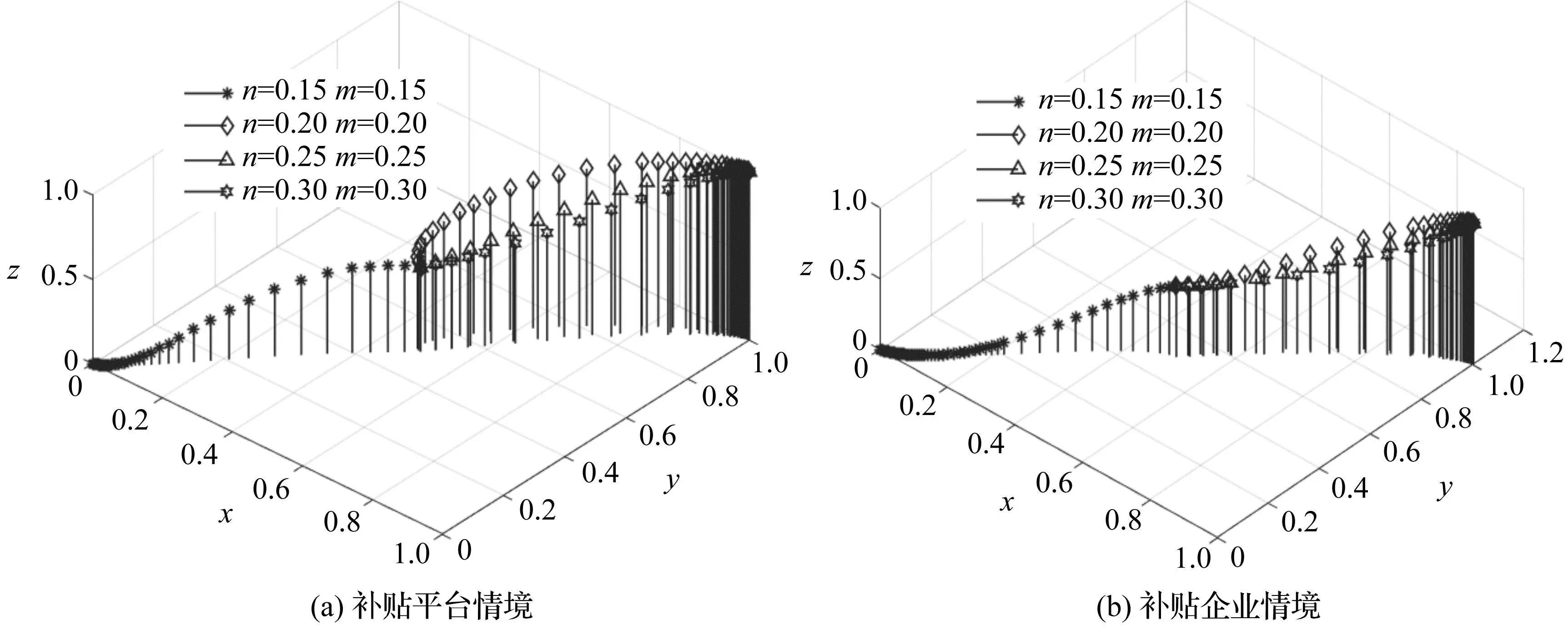
情形1:当nCs 情形2:当nCs 情形3:当Efs-πRs 情形4:当Es1 情形5:当nCs 情形6:当nCs>max{Efs-πRs,Es1},mCd 情形7:当nCs>max{Efs-πRs,Es1},Efd-ωRd>mCd>Ed1,Cp1 情形8:当nCs>max{(1-θ)Et-(β-λ)Rs,Es1},mCd>max{θEt-(β-α)Rd,Ed1},Cp1>max{(1+β)Cp2-Et-Ep+Ed1+Es1-(P2-P1)K,Es1-Efs+(1+π)Cp2-(P2-P1)K}时,G8(1,1,1)为博弈系统的演化稳定点(ESS点),其所对应的演化稳定策略为:资源供给方参与,资源需求方参与,平台提供优化服务。 根据均衡点特征值取值状态对应8种情形,将具体情况在表5中进行汇总。 表5 各均衡点对应雅克比矩阵特征值的符号判断 2.政府补贴供应链企业情境 根据式(13)、式(14)和式(15),能够求出政府补贴供应链企业情境的博弈系统雅克比矩阵J2。 由雅克比矩阵计算结果可得Fx(x,y,z)、Fy(x,y,z)、Fz(x,y,z)表达式,分别令Fx(x,y,z)=0,Fy(x,y,z)=0,Fz(x,y,z)=0,求得资源需求方和工业互联网平台在博弈过程中存在8个纯策略均衡点,分别为G1(0,0,0),G2(0,0,1),G3(0,1,0),G4(1,0,0),G5(0,1,1),G6(1,0,1),G7(1,1,0),G8(1,1,1)。将上述8个纯策略均衡点分别带入系统的雅克比矩阵可求得各均衡点所对应的Jacobian矩阵特征值,如表6所示。 表6 各均衡点对应Jacobian矩阵特征值 类似政府补贴平台情境,对政府补贴供应链企业情境时资源供需双方和工业互联网平台在博弈过程的8个纯策略均衡点的三个特征值进行分析,可得到8种不同的情形。将其具体情况进行汇总,如表7所示。 表7 各均衡点对应雅克比矩阵特征值符号判断 为研究政府不同补贴政策对博弈系统演化的影响,采用Matlab软件进行数值实验。依据参数赋值方法[12-14]并考虑博弈主体之间不同因素变化发生相互作用进行如表8所示的赋值。通过数值实验对演化稳定状态进行分析、验证系统稳定性,研究分析政策补贴不同情境对系统演化结果的影响。 表8 参数赋值情况 本文区分政府补贴企业和补贴平台两种情境进行参数赋值,对三方博弈模型进行了博弈主体初始策略演化分析实验和博弈系统演化路径分析实验。结果显示:博弈主体初始策略会影响系统演化结果,当把博弈三方主体的概率初始策略均设定为0.5时,可消除博弈主体策略初始概率值对系统演化结果的影响;实验验证了模型的稳定性和有效性,受限于文章篇幅,不具体呈现。在博弈初始概率值为0.5和博弈模型有效稳定性的前提下进行系统ESS影响因素数值实验,具体如下: 1.服务费分摊系数对系统演化结果的影响 为研究服务费分摊系数θ在引入政府补贴后对系统演化结果的影响,在其他参数一定的条件下,令θ分别取值为0.3、0.4、0.5、0.7、0.8进行博弈主体策略选择演化数值实验分析。政府补贴平台情境和政府补贴企业情境数值实验结果如下。由图1中(a)可知,随着θ的增大,θ存在两个临界值θ1和θ2决定系统演化稳定的不同状态,临界值θ1位于0.3~0.4之间,临界值θ2位于0.7~0.8之间;当θ<θ1时,资源需求方参与平台提供的优化服务,资源供给方不参与,系统演化稳定于均衡点G5(0,1,1)。当θ1<θ<θ2时,平台提供优化服务且资源供、需双方均参与,系统演化稳定于均衡点G8(1,1,1)。当θ2<θ时,资源供给方参与平台提供的优化服务,资源需求方不参与,系统演化稳定于均衡点G7(1,0,1)。由图1中(b)可知,随着θ的增大,系统演化均稳定于均衡点G8(1,1,1),资源供、需双方均参与平台提供的优化服务,且θ为0.5时,资源供、需双方策略选择相对一致,且双方正向趋近稳定策略参与平台优化服务。 经过实验结果对比分析,若是对服务费分摊系数这一影响因素阻碍了优化式供应链协同的实现,政府补贴企业的效果较优。因为政府补贴企业通过扩大资源供、需双方对服务费分摊系数的可接受范围,提升了供、需双方策略选择参与优化服务的可能性,促进了优化式供应链协同的实现。 2.平台增值服务系数对系统演化结果的影响 为研究平台增值服务系数β在引入政府补贴后对系统演化结果的影响,在其他参数一定的条件下,令β分别取值为0.13、0.23、0.35、0.43、0.63、0.73进行系统演化数值实验。政府补贴平台情境和政府补贴企业情境数值实验结果如下图所示。由图2中(a)可知,随着β值的增大,存在临界值决定系统演化稳定的不同状态。临界值β1位于0.23~0.35之间,当β<β1时,平台提供优化服务,资源供给方不参与而需求方参与,系统演化稳定于均衡点G5(0,1,1),且在此区间内,平台提供优化服务的概率随着β值增大而增强。当β>β1时,平台提供优化服务,资源供、需方均参与,系统演化稳定于均衡点G8(1,1,1),且在此区间内,随着增值服务系数的逐渐增加,平台提供优化服务的概率逐渐降低。由图2中(b)可知,随着的增大,存在两个临界值β1、β2决定系统演化稳定的不同状态,临界值β1位于0.23~0.35之间,临界值β2位于0.63~0.73之间。当β>β1时,此时平台提供优化服务,资源供给方不参与而资源需求方参与,系统演化稳定于均衡点G5(0,1,1)。当β2>β>β1时,此时平台提供优化服务,资源供、需方都参与,系统演化稳定于均衡点G8(1,1,1)。且在此区间内,随着值的增大,平台选择优化服务的概率逐渐降低。当β>β2时,平台选择提供普通服务,资源供、需方都选择参与,演化稳定于均衡点G7(1,1,0)。 图2 增值服务系数β影响示意图 经过实验结果对比分析,若是增值服务系数阻碍了供应链协同的实现,通过政府补贴能有效地进行改善。一是当资源供需方选择参与优化服务的积极性不够,即增值服务系数较低,不足以为资源供、需方带来可图的收益时,政府补贴企业模式能有效调动企业参与优化服务的积极性,促进实现优化式供应链协同。二是当增值服务系数过高,政府补贴平台能缓解平台方的增值成本压力,提供优化服务,促进优化式供应链协同。 3.资源供给方搭便车效应对系统演化结果的影响 在其他参数一定的条件下,以平台协同赋能不同水平β值为背景,观察资源供给方的搭便车效应对系统演化结果的影响,令β分别取值为0.23、0.35,λ为0.1、0.15进行政府补贴两种情境演化数值实验。政府补贴平台情境数值实验结果示意图如图3中(a),政府补贴企业情境数值实验结果如图3中(b)。由图3(a)可知,当β=0.23,λ=0.1和λ=0.15时,系统演化稳定于均衡点G5(0,1,1)。当β=0.35,λ=0.1和λ=0.15时,系统演化稳定于均衡点G8(1,1,1)。由图3中b图可知,当β=0.23,λ=0.15时,系统演化稳定于均衡点G5(0,1,1)。当β=0.35,λ=0.1和λ=0.15以及β=0.23,λ=0.1时,系统演化稳定于均衡点G8(1,1,1)。实验结果表明,当增值服务系数与供给方搭便车效应相差较小且增值服务系数较低时,资源供给方采取搭便车策略。此时,资源需求方参与平台提供优化服务而供给方不参与。 图3 搭便车效应λ影响示意图 经过实验结果对比分析,若是资源供给方搭便车效应阻碍了优化式供应链协同的实现,政府补贴企业的效果较优。通过补贴资源供给方,提高了资源供给方参与优化服务的收益,提升其策略选择参与优化服务的可能性,促进了优化式供应链协同的实现。 4.资源需求方搭便车效应对系统演化结果的影响 在其他参数一定的条件下,以平台协同赋能不同水平的β值为背景,观察资源需求方的搭便车效应α对系统演化结果的影响,令β分别取值为0.2、0.3、0.35,α为0.1、0.15、0.2进行演化数值实验。政府补贴平台系统数值实验结果如示意图4(a),政府补贴企业系统数值实验结果如示意图4(b)。 图4 搭便车效应α影响示意图 由图4中(a)可知,当β=0.2,α=0.1时,系统演化稳定于均衡点G5(0,1,1)。当β=0.2,α=0.15和β=0.3,α=0.2时,系统演化稳定于均衡点G6(1,0,1)。当β=0.3,α=0.15和β=0.35,α=0.1时,系统演化稳定于均衡点G8(1,1,1)。演化结果表明,当平台增值服务系数较低时资源需求方的搭便车效应效果较好时,资源需求方采取搭便车行为。由图4中(b)可知,当β=0.2,α=0.1时,系统演化稳定于均衡点G5(0,1,1)。当β=0.3,α=0.15、0.2和β=0.35,α=0.1时,系统演化稳定于均衡点G8(1,1,1)。当β=0.2,α=0.15时,y、z采用混合策略,博弈系统处于不稳定状态。演化结果表明,资源需求方的搭便车效应是平台增值服务系数较低,且资源需求方搭便车效应较好时,促使其采取搭便车策略。 经过实验结果对比分析,若是资源需求方搭便车效应阻碍了优化式供应链协同的实现,政府补贴企业的效果较优。政府补贴企业情境,提高了资源需求方参与优化服务的收益,提升其策略选择参与优化服务的可能性,促进了优化式供应链协同的实现。 5.服务费对系统演化结果的影响 通过改变优化服务费Et,研究优化服务费对系统演化结果的影响,在其他参数一定的条件下,令Et分别取值为20、26、32、38进行系统演化数值实验。政府补贴平台情境系统数值实验结果如图5中(a),政府补贴企业情境系统数值实验结果如图5中(b)。由图5中(a)可知,在一定取值范围内,随着Et逐渐增加,系统演化先后稳定于均衡点G7(1,1,0)、均衡点G5(0,1,1)。即,当优化服务费逐渐增加,资源需求方稳定策略选择于参与平台优化服务,随着优化服务费的增加,平台方由提供普通服务策略调整为提供优化服务,但,资源供给方搭便车概率逐渐增大并产生搭便车行为,与此同时,平台通过市场观察到资源供给方的参与概率降低,平台提供优化服务的概率也降低。但,鉴于资源需求方的参与,平台尽管提供优化服务的概率降低,最终并未调整策略。由图5中(b)可知,在一定取值范围内,随着逐渐增加,平台提供优化服务的概率逐渐提高,资源供给方选择参与的概率逐渐降低,系统演化先后稳定于均衡点G8(1,1,1)和均衡点G5(0,1,1)。结果表明,当增值服务费逐渐增加,平台提供优化服务的概率逐渐增大,资源供给方面对平台优化服务由选择参与调整为不参与,资源需求方选择参与。 图5 增值服务费Et影响示意图 经过实验结果对比分析,若是增值服务费阻碍了优化式供应链协同的实现,通过政府补贴平台后,能有效降低平台提供优化服务的增值服务费最低门槛,缓解平台提供优化服务的成本压力,通过稳定资源供、需方的策略选择优化服务,促进实现优化式供应链协同。但,如果此时政府补贴企业,将催生资源供给方的搭便车行为,不利于实现供应链协同。 6.平台优化服务基础成本对系统演化结果的影响 通过改变平台优化服务基础成本Cp2,研究其在政府补贴两种情境中对系统演化结果的影响。在其他参数一定的条件下,令Cp2分别取值为13、15、17、19进行系统演化分析。政府补贴平台博弈系统数值实验结果如图6中(a),政府补贴企业情境系统演化数值实验结果如图6中(b)。 图6 优化服务成本Cp2影响示意图 由图6中(a)可知,随着优化服务的成本增加,平台提供优化服务的概率逐渐减小,并未调整策略,但博弈系统均演化稳定于均衡点G8点(1,1,1),即平台提供优化服务,资源供需方参与。由图6中(b)可知,随着平台优化服务基础成本逐渐增加,平台提供优化服务的概率逐渐变小,直至调整策略提供普通服务,系统演化稳定于均衡点G7点(1,1,0)。当提供优化服务的成本超过一定的临界值时,平台不提供优化服务。经过实验结果对比分析,发现优化服务成本改变了供应链协同的实现方式。通过政府补贴平台能有效推动平台提供优化服务,使普通式供应链协同转换为实现优化式供应链协同。 7.平台普通服务成本对系统演化结果的影响 通过改变平台普通服务成本Cp1,研究其在政府补贴两种情境中对系统演化结果的影响。其他参数一定的条件下,令Cp1分别取值为2、4、6、8进行系统演化数值实验。政府补贴平台情境的系统演化实验结果如示意图7中(a),政府补贴企业情境系统的演化实验结果如示意图7中(b)。 由图7(a)和图7(b)可知,随着Cp1取值逐渐增加,存在一个临界值改变系统演化稳定状态,即系统由演化稳定于均衡点G7(1,1,0)转变为均衡点G8(1,1,1)。普通服务成本Cp1的增加,正向促进平台策略选择优化服务,反向促进平台策略选择普通服务,稳定资源供、需方策略选择参与。当普通服务成本Cp1小于临界值时,有助于实现普通式供应链协同。当普通服务成本Cp1大于临界值时,促进实现优化式供应链协同。政府补贴两种情境表现无明显区别。 8.成本节约系数对系统演化结果的影响 通过改变成本节约系数n、m,研究其在政府补贴两种情境中对系统演化结果的影响。在其他参数一定的条件下,令n、m分别取值为0.15、0.2、0.25、0.3进行系统演化实验。政府补贴平台情境中的系统演化实验结果如示意图8(a),政府补贴企业情境中的系统演化实验结果如示意图8(b)。 图8 成本节约系数n、m影响示意图 图8中(a)和(b)可知,随着成本节约系数逐渐增大,博弈系统由演化稳定于均衡点G1(0,0,0)调整为演化稳定于均衡点G8(1,1,1)。成本节约系数正向促进资源供、需方参与优化服务,实现优化式供应链协同。由于博弈主体之间策略选择存在相互学习,通过观察其他策略主体的选择,博弈主体会优化自己的策略,实现相对较好的收益。政府补贴平台情境提升了平台方提供优化服务的积极性。 得出的主要研究结论为:(1)政府补贴企业对服务费分摊系数、搭便车效应影响工业互联网平台赋能供应链协同的实现具有改善作用。(2)政府补贴平台对服务费影响工业互联网平台赋能供应链协同的实现具有改善作用。若是因服务费影响平台赋能供应链协同,只能采取政府补贴平台的模式,促使平台降低服务费,进而提升资源供、需方参与平台服务的积极性。因为,政府补贴企业情况下会催生供应链企业搭便车行为,破坏实现的供应链协同。(3)政府补贴企业和政府补贴平台对增值服务系数、成本节约系数影响工业互联网平台赋能供应链协同适用的实现均具有改善作用。(4)政府补贴两种情境均对普通成本影响工业互联网平台赋能供应链协同无效果。政府补贴平台对优化服务基础成本的影响主要是调整了工业互联网平台赋能供应链协同的模式,由普通式供应链协同调整为优化式供应链协同。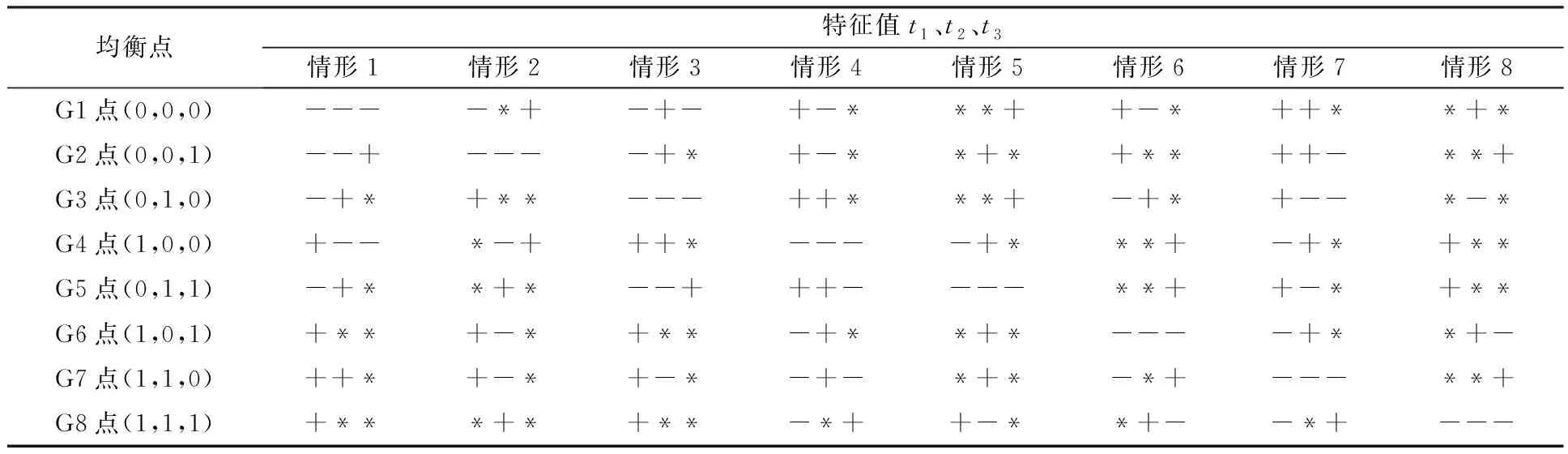

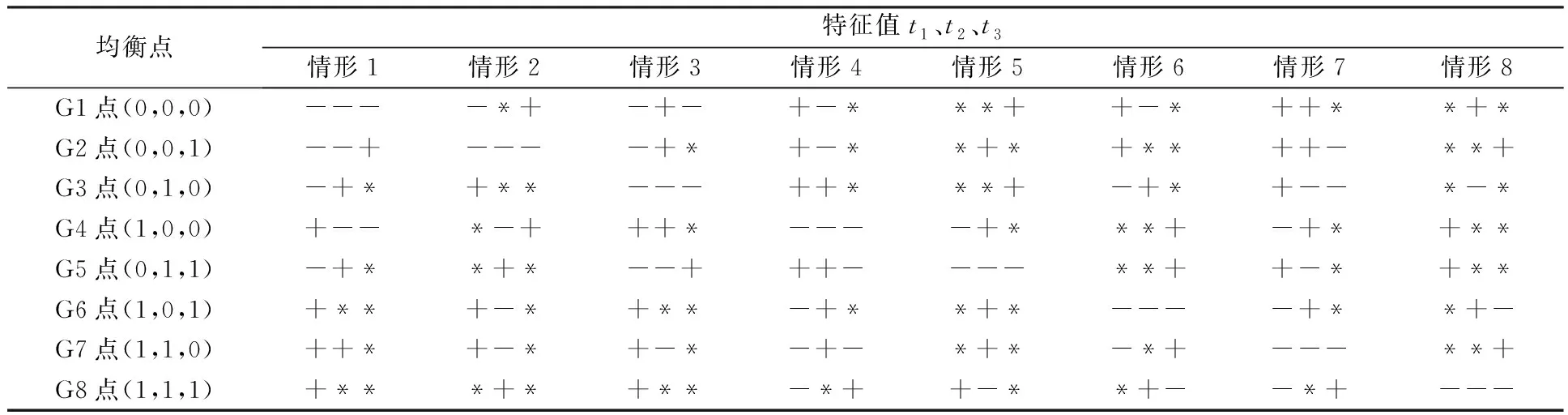
二、数值实验
(一)研究方法与参数赋值
(二)博弈系统ESS影响因素数值实验



三、结论
——基于供需双方的进化博弈

