大挑臂横梁悬浇连续箱梁桥设计要点及受力特性研究
罗致,张焕,老国健
(1.广东省交通规划设计研究院集团股份有限公司,广东 广州 510507;2.广州市高速公路有限公司,广东 广州 510055)
1 引言
随着我国城市化水平的不断提升,交通出行、交通拥堵问题影响着人们的生活,亟待建设更多的城市高架乃至复合型通道[1]。然而,在城市化水平较高的地区建设桥梁往往有着众多的限制因素,既有道路、地下管线、周边房屋、轨道铁路等都会对结构设计及施工方案造成影响,为桥梁建设增大工程难度[2]。
预应力混凝土连续箱梁桥是城市桥梁中常见的结构形式,具有结构刚度大变形小、耐久性好、造价经济等优点[3]。其采用无支架的悬臂浇筑法施工时,对桥下净空影响小[4],有利于城市高架桥建设,能在施工过程中维持桥下道路的正常通行。而合理采用箱梁横梁挑臂的结构形式,能避开桥下沿桥轴线方向上的既有构造物。若将悬浇施工与横梁挑臂的连续箱梁结构相结合,将进一步提高其在众多限制因素下的适应能力。国内对悬浇箱梁及支架现浇连续箱梁挑臂横梁的受力、设计要点已有较多研究成果[4-7],但目前挑臂横梁悬浇连续箱梁桥仍缺少设计案例及相关研究。本文介绍某城市高速上设计的一座大挑臂横梁悬浇连续箱梁桥,并通过空间有限元进行结构分析,重点研究其区别于常规悬浇箱梁桥和支架现浇的挑臂横梁连续箱梁桥的设计要点及受力特性,为同类工程提供参考。
2 桥梁结构的设计要点
2.1 总体布置及截面形式
某新建高速沿城市主干道高架方向建设,与既有高速主线交叉,其建设过程需同时确保桥下城市主干道及既有高速正常运营。且由于交叉节点距离高铁桥梁较近,新建高速在上跨既有高速后在较近距离内需下穿高铁桥梁,因此墩高较矮,不宜采用刚构方案。在设计阶段,从减少对桥下道路干扰、控制造价的角度出发,在交叉节点采用挑臂横梁悬浇连续箱梁桥跨越。桥梁长度163.2 m,跨径组合为(44.1+75+44.1)m,见图1。上部结构为变高连续箱梁,桥宽16.25 m,中支点梁高4.5 m,跨中梁高2.2 m;主墩为2.8 m×2.8 m方墩,其余结构具体尺寸见图2、图3。

图1 连续箱梁总体布置
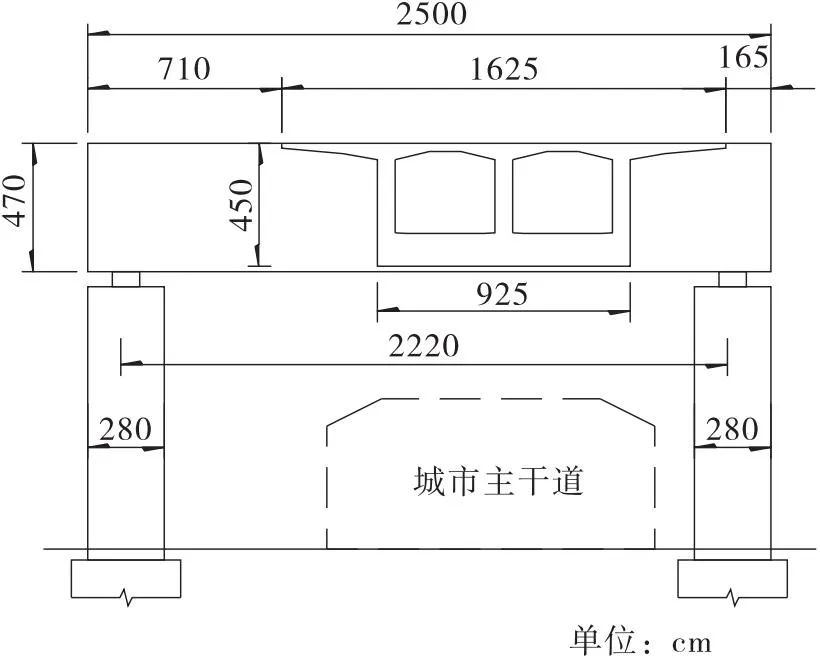
图2 主墩及挑臂横梁横断面
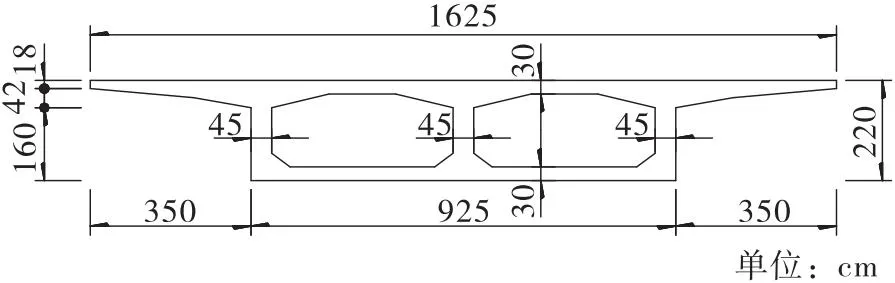
图3 跨中截面标注横断面
2.2 预应力体系

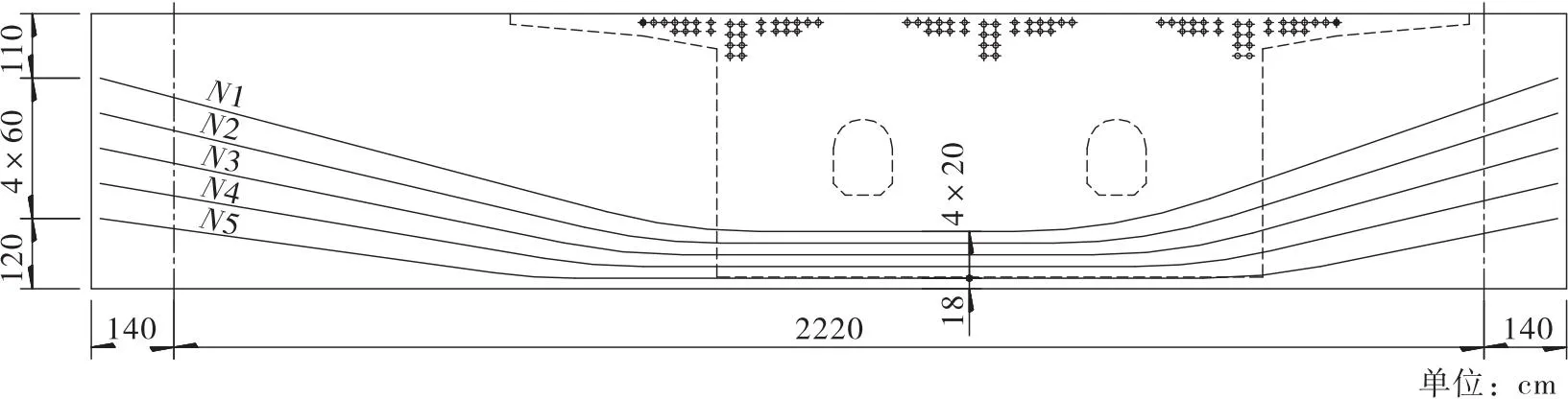
图4 挑臂横梁预应力钢束布置
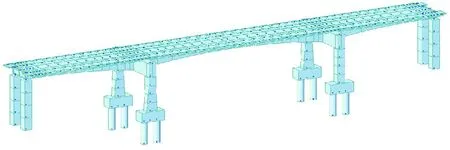
图5 全桥梁格模型消隐图
2.3 挑臂横梁尺寸及配筋
挑臂横梁设计高度略高于主梁支点处高度,便于横梁底缘纵向主筋的布置,避免与主梁纵向钢筋冲突。横梁宽3.0 m,高4.7 m,支点间距22.2 m,其余尺寸详见图2。底缘布置双排间距10 cm、直径28 mm的主筋;为增强其抗扭强度,外圈以10 cm间距布置直径25 mm的抗扭箍筋;横梁内部同样以10 cm间距布置4圈(共8肢)直径20 mm的抗剪箍筋。
3 结构计算分析
3.1 计算模型
采用有限元软件Midas Civil对挑臂横梁悬浇连续箱梁进行计算分析,按实际结构尺寸建模。分别建立空间单梁模型及梁格模型,对比两者的计算结果发现,对于挑臂横梁内力而言两种模型相差较远,其中自重作用下单梁模型横梁最大弯矩为192 634 kN·m,梁格模型横梁最大弯矩为138 988 kN·m。由于单梁模型不能准确反映出主梁质量分布情况,因此横梁计算结果应以梁格模型为准,以下计算分析均采用梁格模型结果。上部结构采用梁格模拟时,纵向以单个腹板划分单元并考虑翼缘有效宽度;悬臂外边缘以虚拟纵梁连接;横向根据结构实际尺寸考虑刚度采用虚拟横梁连接。模型考虑施工阶段的影响。

3.2 计算结果与分析
3.2.1 成桥状态
(1)挠度:不同工况下挑臂横梁及主梁最大挠度见表1,即使考虑挠度长期增长系数后,仍远小于规范[8]规定的L/600(中跨125 mm,边跨73.5 mm)。
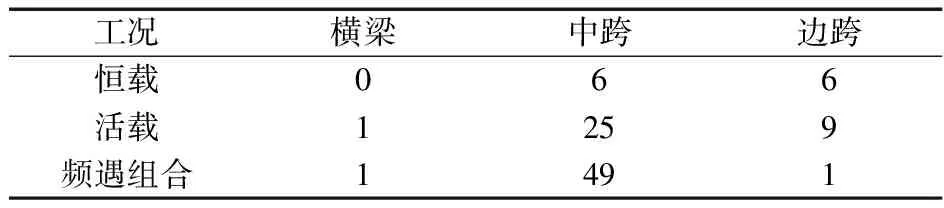
表1 不同工况下横梁及主梁最大挠度 单位:mm
(2)内力:各种工况下主梁、横梁的弯矩及横梁扭矩见图6。由其内力分布情况可知,该结构同时具有常规悬浇箱梁及挑臂横梁现浇箱梁的受力特点,又有所不同:①主梁和横梁的弯矩主要由自重引起,活载作用引起的弯矩较小,主梁中墩负弯矩值较大,横梁基本均为正弯矩;②相对于整体现浇的挑臂横梁结构而言,悬浇施工的主墩挑臂横梁所受重力影响更大,且横梁弯矩值与主梁纵向最大弯矩值相当,在本案例中横梁荷载组合下的最大弯矩值已超过主梁最大弯矩;③横梁的扭矩主要由活载引起,自重引起的扭矩较小,且荷载组合下扭矩值较小,说明该结构在成桥状态下横梁抗扭往往不控制设计。
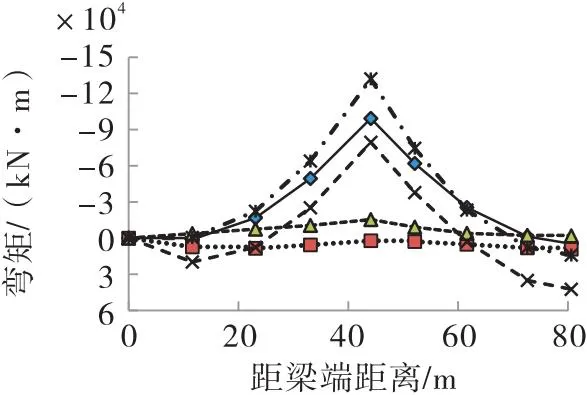
(a)不同工况下主梁弯矩

图6 不同工况下主梁、横梁的弯矩及横梁扭矩注:图中活载max和活载min、基本max和基本min分别指《公路桥涵设计通用规范》中汽车荷载作用下结构响应最大值和最小值、基本组合作用下结构响应最大值和最小值。
(3)横梁应力:主梁的应力特点与常规悬浇箱梁相近,在此仅列出挑臂横梁在不同工况下的应力状态,横梁应力分布如图7所示,图中应力压力为正、拉力为负,图中竖向虚线位置为横梁与主梁外腹板边缘连接部位。由计算结果:①频遇组合下横梁最不利正截面拉应力出现在支点附近顶缘,为1.0 MPa,其余位置基本受压,满足规范A类预应力构件的要求;②标准组合下最不利正截面压应力出现在横梁跨中顶缘,为10.2 MPa,小于规范要求的16.2 MPa;③横梁与主梁连接部位,应力变化平顺未发生突变,考虑弯剪扭共同作用下主拉应力较小,同样满足规范对主拉应力的相关要求[8]。挑臂横梁运营工况下应力状态较好。
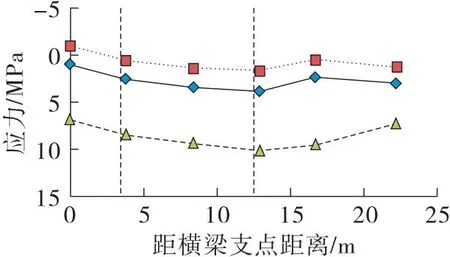
(a)不同工况下挑臂横梁顶缘正截面应力
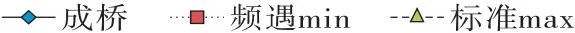
图7 不同工况下横梁应力分布注:图中频遇min、标准max分别指《公路桥涵设计通用规范》中频遇组合作用下结构响应最小值、标准组合作用下结构响应最大值。
3.2.2施工阶段
根据桥梁上部结构尺寸,将其划分为如图8所示的9个悬浇节段,其中第10节段为合龙段。

图8 连续箱梁悬浇节段划分情况
1.预应力张拉顺序
常规的支架现浇连续箱梁施工时,为避免施工过程中钢束引起的反拱效应造成拉应力过大,其主梁、横梁预应力需分批张拉[5]。同样挑臂横梁悬浇箱梁桥也需要考虑横梁钢束张拉顺序与批次,在此设置三种张拉方案:①0号块横梁浇筑完成后一次张拉所有横梁钢束再进行纵梁钢束张拉及悬浇;②0号块横梁浇筑完成后先张拉横梁N2~4钢束,主梁合龙后二期施工前张拉剩余横梁钢束;③0号块横梁浇筑完成后先张拉横梁N2、3钢束,3号块悬浇完成后4号块施工前张拉横梁N1、4钢束,主梁合龙后二期施工前张拉剩余横梁钢束。不同方案横梁跨中顶、底缘应力如图9、图10所示,图中应力压力为正、拉力为负。
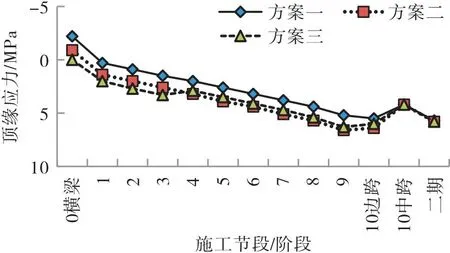
图9 不同钢束张拉方案挑臂横梁跨中顶缘应力
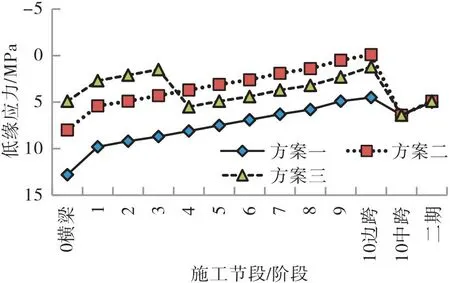
图10 不同钢束张拉方案挑臂横梁跨中底缘应力
由以上应力结果可知,三种方案最终应力状态相同,但张拉批次越多,施工过程中横梁应力水平越均匀:采用方案一钢束一批次完成张拉时,横梁跨中顶缘拉应力2.2 MPa,已超规范1.855 MPa限值,且底缘压应力12.8 MPa较高;方案二施工过程中,应力虽能满足规范要求,但第一批钢束张拉时跨中顶缘出现0.9 MPa拉应力,第二批钢束张拉前最大悬臂状态及边跨合龙阶段压应力储备较小甚至出现轻微拉应力;方案三则整体应力水平均匀,施工过程基本不出现拉应力。综上,设计推荐采用横梁钢束分三批次张拉的方案三。
2.悬臂阶段不平衡荷载工况
悬浇连续箱梁在施工过程中,即使结构对称,不平衡荷载同样难以避免,设计时应对其影响予以充分考虑[9-10]。在此,悬臂阶段不平衡荷载考虑如下:①两侧梁段自重偏差±4%;②桥上不均匀堆载,一侧悬臂8 kN/m均布荷载另一侧空载;③挂篮及模板重量偏差,一端取1.2倍,另一端取0.8倍,其中挂篮及模板重700 kN;④最后一个悬臂段施工不同步,相差一半梁段重量;⑤风荷载。
在悬臂施工阶段不平衡荷载工况下,墩柱及桩基偏心受压验算与常规悬浇箱梁相近,在此仅列出挑臂横梁在最大扭矩下的承载能力验算情况。悬臂施工阶段标准组合下横梁扭矩最大值为30 769 kN·m,根据相关规范[8]进行矩形截面抗剪扭承载力计算,其抗扭承载力为32 423 kN·m,基本满足要求。根据上述结果,在最不利工况下抗扭承载力基本无富余,存在较大安全风险。由于施工期间的不确定因素较多,为确保结构安全,设计提出施工过程控制扭矩不大于23 000 kN·m的要求。施工过程中除采取常规的悬浇箱梁监控手段外,额外提出需通过监测横梁扭转角来确定横梁内力,当出现较大的不平衡荷载时,及时通过临时压重等措施减小横梁扭矩。
4 结论
本研究通过对某大挑臂横梁悬浇连续箱梁桥进行空间有限元结构分析,得出以下结论:
(1)大挑臂横梁悬浇箱梁桥结构计算时,单梁模型不能准确反映横梁内力,计算时上部结构应采用梁格模型进行模拟。
(2)该类型结构刚度较大,结构整体挠度较小,行车舒适性良好。
(3)主梁纵桥向的受力特点与常规悬浇箱梁相同;悬浇施工的挑臂横梁内力相对整体现浇的挑臂横梁结构而言受自重影响更大,横梁弯矩主要由自重引起,且横梁弯矩值较大,在本文案例中横梁弯矩值与主梁中墩墩顶负弯矩相当;而成桥状态下横梁扭矩值较小,基本不控制设计。
(4)该类型结构合理设计时,成桥状态下横梁应力状态较好,横梁与主梁连接部位应力变化平顺,考虑弯剪扭共同作用下主拉应力较小。
(5)横梁预应力钢束张拉批次对施工阶段应力状态影响较大,对成桥应力状态影响较小;设计时应根据悬浇节段划分情况结合计算结果合理确定张拉批次,张拉批次越多施工过程中横梁应力水平越均匀,应尽量避免出现横梁压应力过大或较大拉应力的情况。
(6)悬臂施工状态下不平衡荷载引起的横梁扭矩较大,在本文案例中,最不利施工工况下横梁抗扭承载力基本无富余,有一定安全风险。宜结合横梁扭转角监测控制施工过程中的横梁扭矩,根据检测结果采取临时压重措施。

