史密斯圆图简化传输线教学研究*

徐鹏 吕辉 胡玥 姚育成 李劲 吕清花 马新国

湖北工业大学芯片产业学院 武汉 430068

0 引言

传输线理论是典型场路结合、将“场”的问题用“路”的方法简便处理的电磁理论，将抽象的电磁波传输转化为通俗的电压波、电流波传输以及输入阻抗的动态起伏，传输线的电磁物理参数、几何结构参数相应地转化为传输线特性参数[1-2]。其中，史密斯圆图得到广泛的工程应用[3-9]，但鲜见将史密斯圆图作为纽带，把传输线一系列知识点串联，与理论公式相互映衬，激发学生把控传输线理论框架，降低教学难度的处理方法。本文从物理图像视角重新审视史密斯圆图，并应用史密斯圆图轻松化解阻抗匹配原理、谐振腔等效电导取值范围判据等阐释繁琐的教学难点，使学生不经意间掌握传输线波动的脉搏，提高课堂教学效果。本文所用时谐因子为exp(jωt)。

1 另眼看史密斯圆图

不同于短线，传输线上物理量是分布参数，不仅与时间相关，而且与传输线的空间位置有关[1-2]。传输线的特性参数可类比均匀空间电磁波传播来体味[2,10]。单位长度上的分布电感L和分布电容C分别与磁导率μ和介电常数ε有内在线性关联，如无耗同轴传输线的分布电感和分布电容用其物理参数和几何参数可分别表示为[2]：

其中a和b分别是同轴腔内外半径。所以，一般传输线相位常数都可类似电磁波波数来理解：

即分布电抗与分布电纳积的平方根。推广到分布阻抗与分布导纳积的平方根，则为有耗传输线传播常数：

上式右边单位与传播常数量纲吻合，揭示出其内在的逻辑性。无耗传输线特性阻抗类似波阻抗来认识：

即分布电抗与分布电纳商的平方根。类似地推广到分布阻抗与分布导纳商的平方根，则为有耗传输线特性阻抗：

上式右边单位与特性阻抗量纲吻合，同样表明其内在逻辑性。波阻抗一般是常数，观察上式，特性阻抗又有不同之处，它还与传输线的几何参数有关，并且可能曾现出色散性。

如图1所示，史密斯圆图就是为方便描述传输线特性而应运而生的，其本质是由两套坐标系叠置构成：一套是反射系数Γ实轴和虚轴构成的隐性直角坐标系，其坐标线无需标出，可通过与单位圆半径的相对长度比对而读取；另一套是归一化输入阻抗（或归一化输入导纳）实部和虚部构成的显性曲线坐标系，两套坐标一一对应关系由（6）式确定：

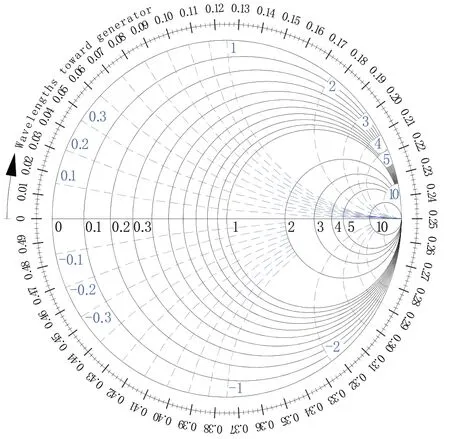
图1 史密斯圆图

上式物理意义清晰：传输线任意位置的归一化输入阻抗就是归一化总电压（入射电压1＋反射电压Γ）除以归一化总电流（入射电流1＋反射电流(-Γ)，注：反射电流与反射电压反相）。通过（6）式实部虚部各自映射关系，在反射系数Γ的直角坐标系中，叠置归一化输入阻抗实部和虚部圆弧坐标系，从而将输入阻抗直观化。考虑在传输线上走位，可直接在曲线坐标系中读出传输线任意点的归一化输入阻抗，避免了通过负载阻抗求取其他位置上输入阻抗的复杂计算：

（7）式是（6）式在无耗时的特例，可从（6）式直接导出。它表明，传输线上归一化输入阻抗按λ/2周期性变化。（7）式可退化为特殊的短路和开路负载传输线上输入阻抗（即退化为纯电抗）：

所以短路和开路负载附近的感抗和容抗交错特性一目了然，（7）式和（8）式可相互提示、映衬。在图1所示单位圆上，也清晰地显示短路和开路负载传输线输入阻抗的周而复始变化规律。如（7）式任意负载传输线，其输入阻抗也在史密斯圆图不同半径的圆周上动态起伏。

受能量守恒的约束，反射系数模值不能大于1，所以图1所示史密斯圆图被限制在反射系数坐标系的单位圆内。从传输线上任意一点向源/负载方向移动，对应史密斯圆图上绕Γ坐标系原点顺时针/逆时针旋转，考虑无耗传输线，则表现为顺时针/逆时针圆周旋转，此对应关系与（9）式相呼应：

上式暗含三层物理背景：传输线关注负载附近参数，所以一般以负载处为z轴原点，正向指向源；故反射电压沿+z轴传播，而+z轴传播时，空间引起相位变化应与时间引起相位变化exp(jωt)相反，故符号取负，入射电压则沿-z轴传播，符号取正，相应地，反射系数的空间相位因子为exp(-j2βz)；此因子表明，向源移动即沿+z轴方向移动，相位变小，对应顺时针旋转，反之则逆时针旋转。Γ的重复周期也为λ/2，与（7）式相呼应。

无耗传输线λ/2的重复性也可直观地从史密斯圆图上看出来，从任意一点沿圆周旋转一圈，对应在传输线上移动了λ/2的整数倍，阻抗参数重回起点。另外，从任意一点旋转半圈，对应在传输线上移动了λ/4的奇数倍，两处的反射系数刚好互为相反数，依据（6）式，它们的归一化输入阻抗互为倒数，此即λ/4的变换性。利用史密斯圆图可方便地读出变换位置后的输入阻抗，避免了（6）式或（7）式的复杂计算。众所周知，任意位置的导纳与阻抗也是互为倒数关系，所以也可方便地利用史密斯圆图读出当前位置的归一化导纳，阻抗圆图即转化为导纳圆图，需注意，是当前位置而不是相隔λ/4不同处的归一化导纳。

在无耗传输线上的移动反映为史密斯圆图上沿圆周旋转，其中有两种特殊的圆周：半径为0的圆（即退化为原点）和单位圆。前者传输行波，参数不随传输线位置移动而变化，即把无反射的Γ=0代入（6）式，或将匹配负载代入（7）式，均有；后者为纯电抗圆，其负载为短路、开路或纯电抗（短路和开路可视为极端的纯电抗），负载不吸收能量，故能量被全反射，即≡1，所以传输驻波。从最左端的短路点出发沿单位圆顺时针旋转，其曲线坐标值即反映了公式（8a）的纯感抗变化规律；从最右端的开路点出发也沿单位圆顺时针旋转，即反映了公式（8b）的纯容抗变化规律；从任意负载出发顺时针旋转，则反映了公式（7）中在传输线上的周期变化。行波与驻波之间的区域即为混波，行波与驻波不仅是混波的边界，也可视为混波的极限特例。在史密斯圆图上每旋转一周，都会穿过Γ实轴（纯电阻坐标线，或视为0电抗半径无穷大的圆弧坐标线）两次。正实轴上反射电压与入射电压同相，为传输线上电压最大的一系列波腹点；负实轴上反射电压与入射电压却反相，为传输线上电压最小的一系列波节点。右端开路点为波腹极限点，左端短路点为波节极限点，两者往中间靠齐，波腹波节起伏趋于平缓，直至中间原点处，波腹波节趋于一致，变成波腹波节消失的行波。波腹电压与波节电压比值构成电压驻波比概念：

对于无耗传输线，任一点的复反射系数Γ，都可通过圆周旋转到Γ正实轴的交点，获取同相值而计算驻波比。但实际中通过史密斯圆图则无需计算，比较（10）式和（6）式就会发现，驻波比就是特殊的归一化输入阻抗，Γ退化为正实数时，驻波比即波腹处的归一化阻抗，且为纯电阻。同理，行波系数是波节处的归一化阻抗（也为纯电阻）：

逆向来看，外接纯电阻负载（含∞和0）一定处在波腹或波节上，归一化后即可得到驻波比或行波系数。需要注意的是，尽管驻波比和行波系数在数值上都等于特殊的归一化输入阻抗，但物理意义不同，前两者都是不同位置的归一化总电压之比，而后者是同一位置的归一化总电压与归一化总电流之比，在教学时需交代清楚。这样，传输线的驻波比和行波系数可方便地通过纯电阻线上的曲线坐标值读取。显而易见，驻波比和行波系数也具有λ/4的变换性，短路（K=0）和开路（S=∞）是一对极端变换，匹配点（行波）处驻波比和行波系数都趋于1，是另一对极端变换。另外，行波系数K∈[0,1]，但并不完全反映行波成分的权重。

2 从史密斯圆图看阻抗匹配

厘清了史密斯圆图的脉络，再来审视阻抗匹配。负载与传输线匹配，将吸收全部入射波能量，传输线上载行波。阻抗失配会产生反射波，降低传输线效率，支节匹配器本质上是在负载附近加载逆向电抗/电纳器件，使得在负载和加载器件之间形成内部反复充放电过程，即反射波在内部进行，从而减少对主线传输入射波的影响。一般在微波技术类课程讲授支节匹配器原理中，文字阐释较复杂，理解变得困难。若辅以史密斯圆图，揭示从负载导纳趋向匹配负载（即Γ坐标系原点处行波）的轨迹，将使得匹配原理图像化，令课堂教学更轻松、学生更易于理解和接受。

图2a所示单支节匹配器，BB处负载ZL不匹配，拟在主线合适的位置AA处加载一短路或开路支节（提供纯电抗/电纳蓄能池），吸收BB处反射能量，在下半个周期又释放给ZL，使得AA之前的主传输线传输行波，需设计支节长度LS和在主线上的位置L。并联支节的导纳可直接相加减，此处使用导纳比阻抗更简便，故在图3a中，归一化负载阻抗经过180°旋转到达归一化负载导纳，接下来史密斯圆图化为导纳圆图，短路点和开路点对调，分别位于圆图的最右端和最左端。

图2 传输线支节匹配器

图3 史密斯圆图显示阻抗匹配轨迹

单支节匹配结构简单，但支节在主线上移动定位，需焊接易致接触不良。图2b所示双支节匹配器克服了这种缺陷，两支节固定在主传输线上并不移动，支节1的位置L直接锁定，两支节相距λ/8（也可λ/4或3λ/8），需要设计的仅是两个支节的长度LS1和LS2，短路还是开路支节可从节省材料角度取舍。

3 从史密斯圆图看谐振腔品质因数测量

谐振腔的并联等效电路在谐振频率附近具有三个特点：等效电导为常数，电纳随频率线性变化，且在谐振频率f0时为0。其品质因数可表示为[1,11]：

上式可作为一种测量Q值的依据，但需判断电导的取值范围，以便通过测量驻波比得到电导：

在实验教学中[11]，不少学生理解<1还是>1的判据有困难。利用史密斯圆图却能一目了然地阐释。

如图4所示导纳圆图，谐振时，驻波比最小，负载和波节均在Γ实轴上（即纯电导坐标线上），随着频率降低，依（12）式电纳为负，负载即在如图所示的等电导弧线上向右滑落，而波节仍在Γ实轴（也是0电纳线）上平移。图中标出了不同频率下谐振腔负载L0、L1、L2和L3依次到最近波节的距离（圆图上显示为顺时针旋转的弧线电长度）。L0、L1、L2和L3实际是同一个实体，其空间位置不变，最近的电压波节点则是不断移动的。然而在史密斯圆图上显示为，负载不断在等电导线上变换虚坐标位置，而波节却有在电刻度0.25λ处固定不动的错觉，所以需想象传输线实际波动与在史密斯圆图上抽象跳跃的关联。

图4 史密斯圆图判断等效电导取值范围

图5导纳圆图显示了如何通过驻波比测量品质因数。用上述方式判定电导，若<1，再通过测出谐振频率时的驻波比，确定传输线上走位所对应的旋转圆周找到电导，图中取=0.3值。微调频率后重测驻波比，负载导纳同时满足在等驻波比圆周上旋转，和在等电导圆=上滑动，每次相交两点，频率低于谐振频率则电纳取负值（如点f⇓＜f谐振和点f↓＜f谐振），反之则取正值（如点f↑＞f谐振），图5清晰地反映了从驻波比，到等驻波比圆，再到与等电导圆相交，读取电纳的物理图像过程。利用最小二乘法处理电纳与频率线性变化的斜率，可比较精确地测出谐振腔的品质因数。

图5 史密斯圆图揭示谐振腔品质因数测量原理

学生在实际测量中，往往会流于照搬实验操作步骤，知其然而不知其所以然，尽管完成了谐振腔品质因数的测量，但对原理的理解和物理图像的把握上会有欠缺，教学效果也会打折扣。

4 结束语

传输线广泛应用于雷达、通信和半导体技术，而史密斯圆图暗藏传输线诸多原理，且便于工程应用。史密斯圆图与理论公式相结合，串起了传输线那点事，揭示出传输规律和物理图像框架，形象勾勒出传输线参数在史密斯圆图上的起伏跳跃。不仅达到微波技术课程教学难度降维的显著效果，而且使学生张开想象的翅膀，轻松掌握传输线基本概念、传输规律、和应用方法，极大激发了该类课程的学习兴趣和激情。