低信噪比下的滚动轴承早期微弱故障识别∗

张 赟， 王永华， 唐岩辉， 韦 祥， 王景霖

（1.海军航空大学航空基础学院 264001，烟台）

（2.故障诊断与健康管理技术航空科技重点实验室 上海，201601）

引 言

在滚动轴承发生故障的初期，由于损伤性很小，产生的故障信号不太强烈。此外，轴承信号在传递至振动传感器的过程中会发生衰减，而且会受到机械系统其他转动部件产生的激振源（转子不平衡、齿轮啮合等）的影响，使得原本不太强烈的轴承故障信号会被周围的激振源噪声干扰所掩盖，因此实现滚动轴承早期故障的微弱信号提取是一个难点问题。

理想的轴承故障振动信号是以轴承相关结构的固有频率为载波频率和故障特征通过频率为调制的振动信号。目前，应用于滚动轴承微弱故障提取与识别的方法主要有时域分析、频域分析、小波分析、经验模式分解及变分模态分解等时频域分析［1-11］。基于希尔伯特变换解调的包络谱分析法是一种已得到广泛工程应用的轴承故障检测经典方法，但是该方法只对故障特征较为明显的信号分析效果好，一旦信噪比过低时，就难以准确提取出掩盖在背景噪声中轴承微弱故障冲击信号的包络，导致诊断失败。小波分析法依赖于小波函数的合理选取以及对分解后的子带信号人为选取包含故障信息的分量，受主观影响大。经验模式分解法虽然能够自适应地分离信号中的分量，但缺乏数学理论，存在模态混叠和端点效应。变分模态分解法受参数影响较大，导致信号出现过分解或欠分解。这些方法的缺点使其对轴承微弱故障提取与识别存在一定的局限性。

轴承外圈、内圈或滚动体缺陷故障产生的冲击响应会与轴承系统产生共振，在频域中形成共振频带，故障信息都包含在共振频带中，因此将共振频带的信号提取出来就能获得轴承缺陷冲击特征，实现故障精准检测［12］。谱峭度法是近年来发展起来的4阶谱统计量，通过分析整个频带内信号谱峭度大小，能够有效地发现冲击信号所处的共振频带中心频率及其带宽，设计带通滤波器提取故障冲击信号，再进行包络谱分析实现故障频率特征检测［13-15］。该方法在滚动轴承故障诊断中得到了一定的应用［14-18］，但这些研究集中于故障特征较为明显的轴承故障数据，而直接采用包络谱分析同样能够实现故障诊断。笔者对滚动轴承从完好逐渐发展到损伤失效的全寿命周期试验数据进行分析，结果表明，对于轴承出现的早期微弱故障，谱峭度法能够通过识别提取位于高信噪比共振频带的微弱故障信号，比直接采用包络谱法提前检测出轴承早期微弱故障。

1 基于短时傅里叶变换的谱峭度算法

峭度和谱峭度都能表示信号的非高斯性，前者用在时域条件下，后者用在时频域条件下。

在非平稳条件下，非平稳信号Y(t) 的World-Cramer 分解的频域表达式为

其中：H(t，f)为系统传递函数的傅里叶变换，可以理解成信号Y(t) 在时间t、频率f处的复包络；dX(f)为具有平坦频谱信号X(t)的谱过程。

定义S2nY(f)为Y(t)的n阶谱矩

从能量的角度解释，S2nY(f)被看作是复数包络度量|H(t，f)dX(f)|2n在每个频率f处的时间平均，同样其也可以度量复数包络的能量在时间方向上变化的多少，则Y(t)的4 阶谱累积量定义为

可以证明，当一个信号越偏离高斯性，其4 阶累积矩值就越大。因此，能量归一化后的4 阶谱累积矩可以用来测量信号过程的概率密度函数在频率f处的峰值点。谱峭度即为归一化后的4 阶谱矩，即

设Yw(t，f)为信号Y(t)的短时傅里叶变换（short time Fourier transform，简称STFT），并定义Yw(t，f)的n阶谱矩为

基于STFT 信号Y(t)的谱峭度为

谱峭度就是在STFT 时频面内对于每个频率点f沿着时间t方向计算峭度，从而得到每个频率点处的峭度。正如时域峭度能够反映信号在时域的非高斯性，谱峭度则能够衡量出信号在每个频率f处偏离高斯性的程度。如果偏离高斯性程度越大，对应的谱峭度则越大。因此，谱峭度对非平稳信号（瞬态冲击信号）较为敏感，并且可以找出其存在的频带。瞬态冲击响应信号占主导频带内的谱峭度较大，而平稳高斯背景噪声信号占主导频带的谱峭度很小。通过比较谱峭度的大小，可以将谱峭度较大的频带信号分离出来，从而得到瞬态冲击故障信号。

2 基于谱峭度的滚动轴承早期微弱故障识别

设测量的轴承振动信号z(t)为

其中：n(t)为其他激振源耦合形成的加性平稳高斯背景噪声；y(t)为由轴承外圈、内圈或滚动体缺陷产生的冲击力激发的轴承系统共振响应。

其中：yk为第k个脉冲的幅值；τk为第k个脉冲发生的时间；h(t-τk)为单个冲击引起的脉冲响应。

假定噪声服从稳态高斯分布，则测量的轴承振动信号z(t)的谱峭度为

其 中 ：KY(f) 为y(t) 的 谱 峭 度 ；ρ(f)=SY(f)/SN(f)为信噪比；SY(f)和SN(f)分别为故障冲击响应信号y(t)和噪声n(t)的功率谱密度。

由式（9）可以看出，谱峭度在平稳高斯噪声占主导的频率段处（信噪比ρ(f)低）的谱峭度值接近于0，在故障冲击响应信号占主导的频率段处（信噪比ρ(f)高）的KX(f)接近于KY(f)，此时谱峭度值较大。因此，可以根据谱峭度大小来设计滤波器，把峭度值较大的频带内信号提取出来，从而得到故障冲击响应信号。

谱峭度的估计依赖于窗函数长度Nw的选择，Nw太小会降低频率分辨率，丧失信号的细节；Nw也不能太长，应小于相邻两暂态故障信号的平均间隔。文献［14］引入了峭度图的定义，如图1 所示。峭度图是一个关于频率f和窗长Nw的函数，在谱峭度图中寻找谱峭度最大值（或局部最大值）对应的最优频率f和最优窗函数长度Nw，再以f作为滤波器的最优中心频率，以fs/Nw（fs为采样频率）作为带宽来设计窄带带通滤波器，对信号进行滤波处理得到滤波后的轴承故障冲击响应信号，最后采用包络谱分析并识别其故障特征频率成分。基于谱峭度的滚动轴承早期微弱故障识别流程如图2 所示。

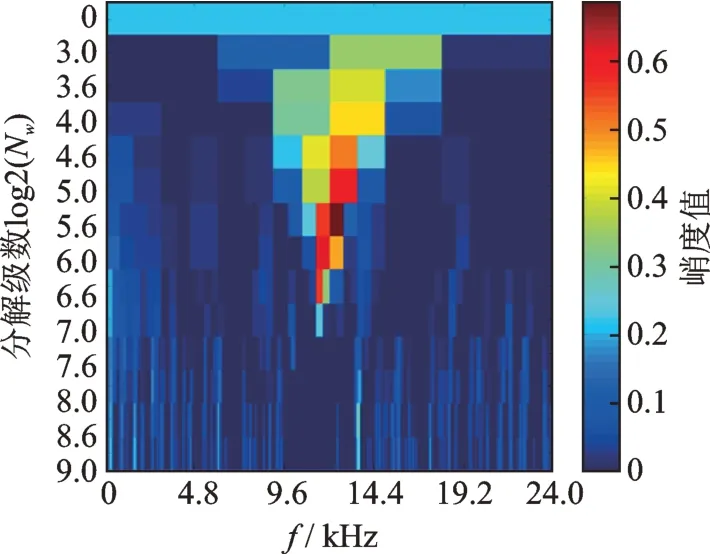
图1 峭度图Fig.1 The kurtogram

图2 基于谱峭度的滚动轴承早期微弱故障识别流程Fig.2 The flow of early weak fault recognition for rolling bearing based spectral kurtosis

3 试验分析

数据来源于美国智能维护系统中心提供的从轴承完好到外圈损伤失效的全寿命周期试验数据。轴承试验装置如图3 所示，4 个ZA-2115 型滚动轴承支撑1 个转轴，电机通过传动带驱动转轴以2 000 r/min 的转速运行，对轴承加载了26 690 N的径向载荷，轴承1 为试验轴承，在轴承1 上安装了加速度传感器，振动采样频率为20.48 kHz，每间隔10 min 采集并记录1 组振动信号，采样时间为1 s，采样点数为20 480。润滑油路中安装了磁塞用于收集金属屑末，当轴承损伤产生的金属屑末累积含量超过限制值后停止试验。轴承的尺寸参数及故障特征频率如表1 所示。

表1 轴承的尺寸参数及故障特征频率Tab.1 Geometric parameters and fault characteristic frequencies of the tested bearing

图3 轴承试验装置Fig.3 The bearing test rig

试验持续了7 天，直到发现磁塞上的金属屑末量显著异常，对滚动轴承1 进行检查，发现其外圈出现了明显的损伤缺陷。滚动轴承1 从正常状态到失效的整个寿命周期的振动信号均方根值（root mean square， 简 称RMS）的 变 化 趋 势 如 图4 所 示（只显示了轴承运行4 000 min 到最后失效的数据）。由图4 可以看出，在轴承运行最后阶段（约9 500 min之后）已处于严重损伤故障状态时，RMS 值显著增大。如果能提前检测到轴承早期损伤故障，对预防轴承损坏的意义重大。考虑到损伤是一个从微弱缺陷到严重缺陷逐渐发展的过程，选取两个不同阶段的数据进行分析，分别是从第7 天RMS 值开始有较大程度增长和波动变化时的数据（对应图中的阶段2 数据），以及第6 天之前的RMS 变化非常不明显阶段的数据（对应图中的阶段1 数据）。

图4 全寿命周期内轴承振动均方根值变化趋势Fig.4 The RMS of bearing in the whole life cycle

3.1 阶段2 数据分析

选取阶段2 初期第7 130 min 采集的轴承振动数据进行分析，此时RMS 值已有一定增长变化，其振动时域信号见图5，可以看到明显的由轴承缺陷引起的周期性冲击信号。轴承运行7 130 min 的振动信号包络谱见图6，在236 Hz 及其倍频处可见明显的峰值，这正对应了外圈故障特征频率，说明轴承运行到7 130 min 已出现了较为严重的外圈损伤，直接采用包络谱分析就能够识别出轴承外圈故障。

图5 轴承运行7 130 min 的振动时域信号Fig.5 The vibration signal as the bearing runs 7 130 min

图6 轴承运行7 130 min 的振动信号包络谱Fig.6 The envelope spectrum of vibration signal as the bearing runs 7 130 min

采用谱峭度法对该轴承振动信号进行分析，得到轴承运行到7 130 min 的信号谱峭度图，如图7 所示，可以看到当频率f=7 680 Hz、窗长度Nw=23.5时谱峭度达到最大值4.9。因此，采用中心频率为7 680 Hz、带宽为fs/Nw=1 810 Hz 的带通滤波器对信号进行滤波，谱峭度法滤波提取后的时域信号及包络谱见图8，同样能够从包络谱中清晰地看见外圈故障特征频率235.9 Hz 及其倍频处有明显的峰值。

图7 轴承运行到7 130 min 的信号谱峭度图Fig.7 The kurtogram of signal as the bearing runs 7 130 min

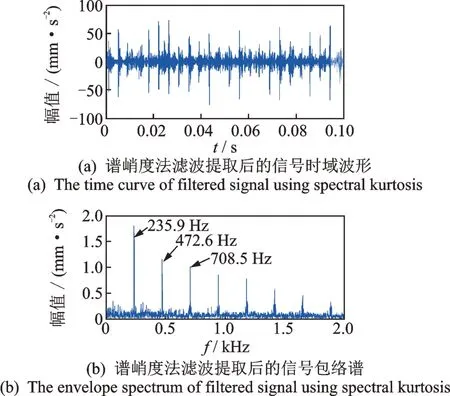
图8 采用谱峭度法滤波提取后的时域信号及包络谱Fig.8 The filtered signal and its envelope spectrum using spectral kurtosis method

3.2 阶段1 数据分析

直接采用基于希尔伯特变换解调的包络谱方法对轴承第1 阶段运行的所有数据逐一进行分析，发现当轴承运行到第5 330 min 时，包络谱分析法开始检测到外圈故障特征频率成分，其时域信号及包络谱分析结果如图9 所示，可以看到明显的236 Hz 的外圈故障特征频率。采用谱峭度法对第5 330 min时的数据进行分析，得到如图10 所示的谱峭度图，当频率f=7 680 Hz、窗长度Nw=24时，谱峭度达到最大值0.8。以7 680 Hz 为中心频率、fs/Nw=1 280 Hz 为带宽设计带通滤波器对信号进行处理，得到滤波后信号的时域波形及包络谱如图11 所示，可以看到236.3 Hz 的外圈故障特征频率，说明谱峭度法也能够检测出轴承外圈早期故障。

图9 轴承运行到5 330 min 的时域信号及包络谱Fig.9 The signal and its envelope spectrum as the bearing runs 5 330 min

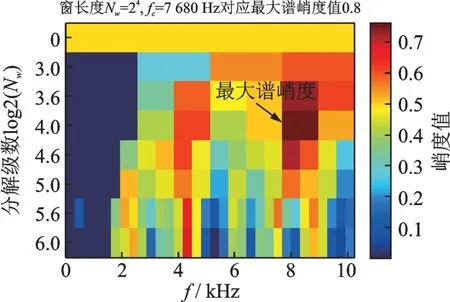
图10 轴承运行到5 330 min 的信号谱峭度图Fig.10 Kurtogram of signal as the bearing runs 5 330 min

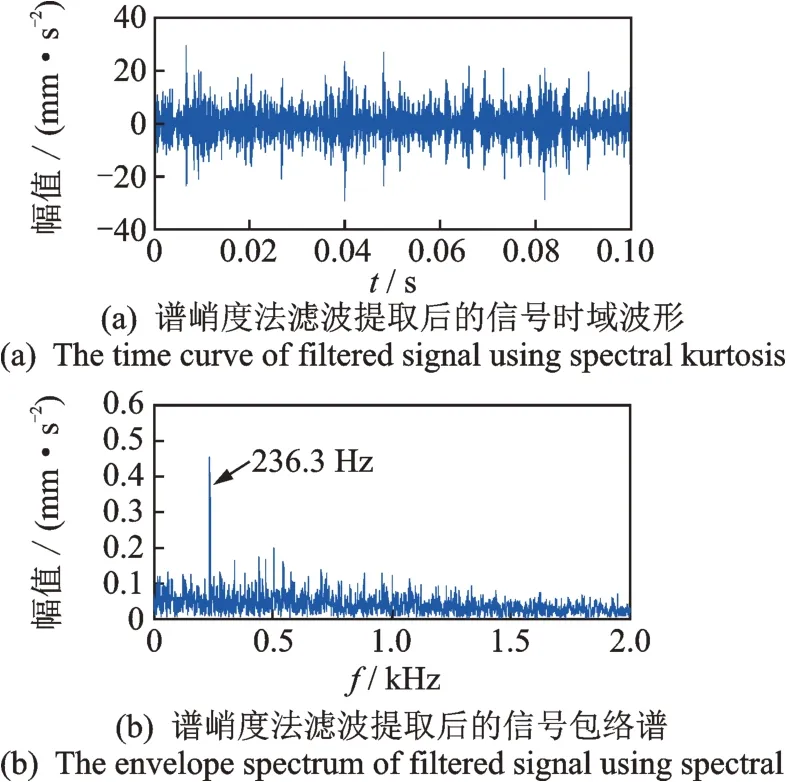
图11 采用谱峭度法滤波提取后的时域信号及包络谱Fig.11 The filtered signal and its envelope spectrum using spectral kurtosis method

针对包络谱法无法检测出故障的数据（即轴承运行5 330 min 之前的数据），采用谱峭度法进一步分析，则在轴承运行第5 130 min 时就能够检测到故障，比直接采用包络谱法提前了200 min。图12 为轴承运行到5 130 min 的时域信号及包络谱，从时域上难以发现微弱故障产生的周期性冲击成分，从包络谱上也无法看到外圈故障特征谱结构，说明直接采用包络谱法无法判断轴承是否出现了早期损伤。

图12 轴承运行到5 130 min 的时域信号及包络谱Fig.12 The signal and its envelope spectrum as the bearing runs 5 130 min

图13 为轴承运行到5 130 min 的信号谱峭度图，最大谱峭度对应的频率和窗长度分别为7 680 Hz 和23.5。采用中心频率为7 680 Hz、带宽为1 810 Hz 的带通滤波器提取出的信号时域波形及其包络谱见图14，从包络谱上能够看到明显的235.9 Hz 频率幅值，这与236.4 Hz 的外圈故障特征频率理论值相吻，说明轴承运行到5 130 min 时就已经出现了微弱的外圈早期损伤。试验结果表明，当试验轴承出现早期微弱损伤故障时，由于信噪比很低，故障特征被背景噪声所掩盖，直接采用包络谱分析法无法诊断出故障，而谱峭度法却通过准确识别提取位于高频共振带的微弱故障冲击信号，能够有效实现轴承的早期微弱故障检测，且比直接采用包络谱法提前200 min 检测到故障。

图13 轴承运行到5 130 min 的信号谱峭度图Fig.13 Kurtogram of signal as the bearing runs 5 130 min

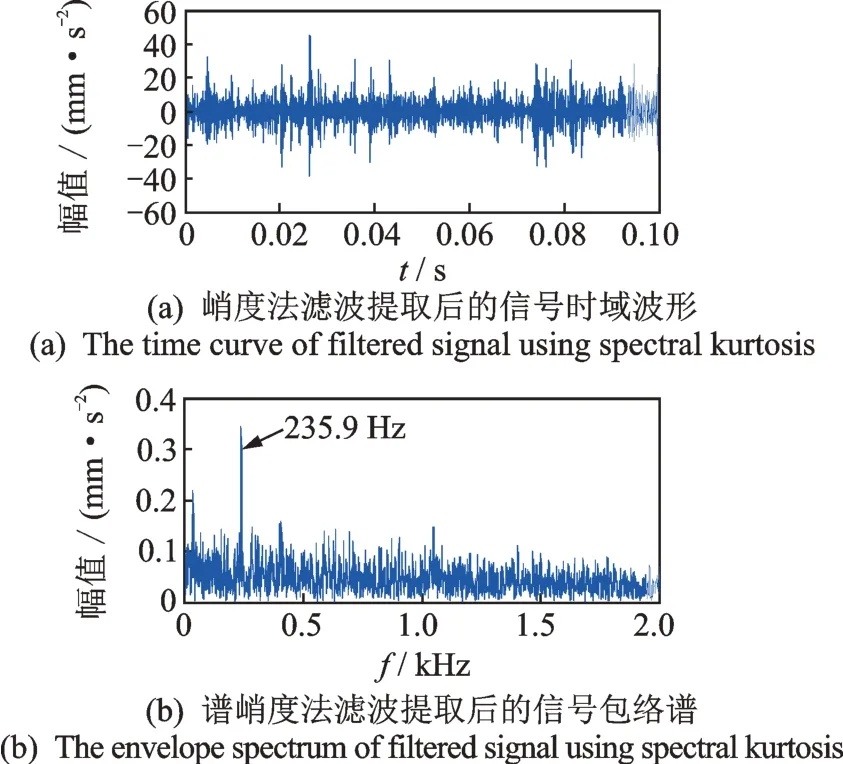
图14 采用谱峭度法滤波提取后的时域信号及包络谱Fig.14 The filtered signal and its envelope spectrum using spectral kurtosis method

4 结束语

轴承早期损伤故障信号会被周围的激振源噪声干扰所掩盖，实现低信噪比下的滚动轴承早期微弱故障识别，对提前预防轴承损坏意义重大。经典的包络谱方法不适合处理信噪比过低的轴承早期损伤故障数据。谱峭度方法是近年发展起来的基于高阶统计量的共振带冲击特征提取方法，适用于处理低信噪比数据。笔者采用谱峭度方法对滚动轴承全寿命周期试验数据（从完好逐渐发展至损伤失效）开展分析，并与经典包络谱方法进行了对比。结果表明：当试验轴承出现早期微弱损伤故障时，由于信噪比很低，故障特征被背景噪声所掩盖，直接采用包络谱分析法无法诊断出故障，而谱峭度法能够准确识别位于高频共振带的微弱故障冲击信号，从而有效实现轴承的微弱故障信号检测及早期故障预警。