铣削工况下考虑结合面的主轴系统动态特性∗
姜彦翠, 陈兴儒, 罗广丹, 刘献礼, 仇 焱
(哈尔滨理工大学先进制造智能化技术教育部重点实验室 哈尔滨,150080)
引 言
数控机床是现代生产、制造过程中的重要加工设备,其性能优劣主要是根据加工工件的尺寸精度和表面加工质量来评定的,这些因素均受到数控机床主轴系统动态特性的影响。主轴系统结构复杂,主要包括主轴、刀柄及铣刀等部件,各结构和部件间通过结合面连接而成,预测其动态特性,需要建立一个有效而精确的模型,进而获得模态参数[1]。由于系统结构中刚度和阻尼很大比例来自于结合面,主轴系统动态特性受到结合面的接触特性影响很大。主轴结合面主要为主轴-刀柄-铣刀结合面和主轴-轴承结合面,而且在铣削工况下,主轴结合面受到离心力、陀螺力矩和铣削载荷等作用,其接触特性与静止状态和空转状态下均有变化。因此,考虑铣削工况结合面的影响,获得确切的主轴系统动态特性,对铣削稳定和提高工件表面加工质量非常重要。
一些学者针对主轴结合面进行了研究[2-3],通过理论分析或实验测试建立结合面接触刚度模型。在主轴系统动态特性研究中,很多都考虑了主轴-刀柄-铣刀结合面的影响。Schimitz 等[4]提出了导纳耦合子结构分析法(receptance coupling substructure analysis,简称RCSA),通过在结合面添加弹簧阻尼单元,借以等效结合面的刚度和阻尼特性,进行特征参数辨识,进而预测刀尖频响函数。许多学者对RCSA 法进行了改进[5-7],预测了不同铣削加工设备的动态特性。有别于RCSA 这种半理论法,赵万华等[8]通过理论分析建立主轴-刀柄-铣刀结合面的解析模型,并将其引入主轴系统理论模型中。在此基础上,文献[9]考虑了离心力和轴向力对主轴-刀柄-铣刀结合面的影响。
此外,主轴-轴承结合面同样对主轴系统动态特性有重要影响。Bert 等[10]基于Timoshenko 梁 理 论建立了主轴-轴承耦合系统的动力学模型。Li 等[11]预测了轴承和主轴的力热特性。文献[12]建立了包括主轴、刀柄、轴承、轴承座和机床支架的动力学模型。文献[13]针对高速电主轴建立了自由状态和工作状态下的动力学模型,并分析了工作状态下主轴转速对主轴系统动态特性的影响。Long 等[14]研究了主轴-轴承结合面动力学特性随转速变化的规律。Xi 等[15]提出考虑主轴壳体和多种形式轴承组合的主轴系统的动力学模型,分析了不同转速下主轴系统刀尖频响函数,研究了几种切削载荷下主轴轴承系统的时程响应。张正旺等[16]综合主轴结合面非线性接触力,对主轴系统非线性动力学特征进行研究。Xu 等[17]利用子结构耦合法进行主轴-刀柄结合面参数识别,利用赫兹理论建立主轴-轴承接触刚度模型,并预测主轴系统动态特性。
学者们对于主轴系统动态特性的研究重点主要集中在主轴系统空转状态下的主轴结合面接触刚度的软化效应对系统动态特性的影响,而笔者则针对铣削工况下高速旋转并受铣削载荷作用的主轴系统进行了研究。首先,考虑铣削工况下径向铣削载荷、轴向铣削载荷、主轴旋转离心力和陀螺力矩,建立了主轴结合面的解析模型;其次,将其与主轴系统动力学模型进行耦合,得到系统动力学耦合模型,并通过在铣削过程中机床主轴系统动态特性实验测试,验证了理论模型的准确性;最后,分析主轴转速、径向铣削载荷和轴向铣削载荷等因素对主轴结合面刚度特征和系统动态特性的影响规律。
1 铣削工况主轴系统结合面接触特性
1.1 主轴-刀柄-铣刀结合面接触刚度
数控加工中心主轴-刀柄-铣刀结合面由液压装置和机械夹紧装置进行预紧连接,在此作用下使得结合面产生接触刚度和接触阻尼。铣削状态下主轴-刀柄-铣刀结合面刚度特征发生改变,主轴系统受力分析如图1 所示。其中:Fx,Fy和Fz为轴向铣削载荷;Fr为径向铣削载荷Fr2分别为前后轴承支撑力;F0为主轴与刀柄夹紧的拉杆力;M0为刀柄与铣刀的预紧力矩。结合面受预紧力、轴向铣削载荷Fz和径向铣削载荷Fr的作用,主轴-刀柄结合面和刀柄-铣刀结合面的平均法向力Pn1和Pn2分 别 为
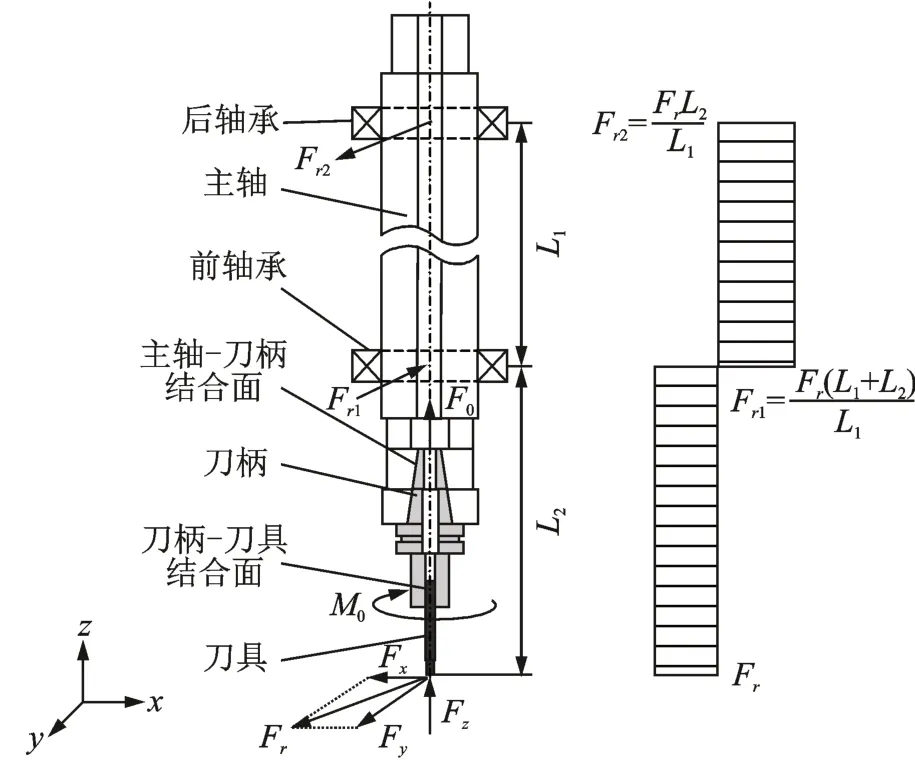
图1 主轴系统受力分析Fig.1 Force analysis of spindle system
其中:Fn1,Fn2分别为主轴-刀柄和刀柄-铣刀结合面法向力;S1,S2分别为主轴-刀柄和刀柄-铣刀接触面积;ϕ1,ϕ2,ϕ3分别为刀柄夹角、夹紧件-刀柄夹角和夹 紧 件-螺 母 夹 角;L1,L2分 别 为 主 轴-刀 柄 和 刀柄-铣刀结合面轴向长度;r1,r2分别为结合面大半径和小半径;μ1,μ2,μ3,μ4分别为主轴-刀柄、夹紧件-铣刀、夹紧件-刀柄及夹紧件-螺母摩擦因数;r3为铣刀半径;k0为预紧力矩系数;d为预紧螺母螺纹外径。
以主轴-刀柄-铣刀结合面中某截面为例,其径向铣削载荷下的弹性变形如图2 所示。结合面的接触正压力发生变化,即

图2 径向铣削载荷下主轴-刀柄-铣刀结合面中某截面变形Fig.2 Deformation of an interface in spindle-tool holder-tool interface under radial milling load
其中:Pr为受到径向铣削载荷后的结合面接触正压力;Pn为仅在预紧力作用下的结合面接触正压力;k(δ)为接触压力系数,可由吉村允孝积分曲线变换求得;δrm为径向铣削载荷作用下结合面内部件变形最大量,δrmFr R2,E为弹性模量,υ为泊松比,R为圆柱结合面半径。
对于圆柱形结合面,由吉村允孝积分法[18]可以得到结合面的等效弹簧刚度为其中:α0,β0为结合面的接触特性参数,主要受到结合面处材料性质、材料粗糙度等物理特性因素的影响;L为圆柱结合面的长度。
在铣削工况下,依据弹性力学理论,在平面应变下,当主轴转速为n,则离心力为ρn2R,结合面间将存在径向间隙,其大小为
其中:b为主轴外径。
结合面的径向间隙在离心力的作用下发生变化,进而使结合面接触正压力发生变化,因此结合面的接触刚度发生变化。
通过主轴-刀柄-铣刀结合面接触刚度理论模型分析,得到径向铣削载荷、轴向铣削载荷和主轴转速对于结合面刚度的影响,分别如图3~5 所示。由图可知:随着主轴转速的增加,结合面接触刚度下降,尤其在较高速时下降更为明显,即离心力对于结合面接触刚度有明显的弱化作用;径向铣削载荷对于结合面接触刚度同样表现为弱化作用;轴向铣削载荷对于结合面接触刚度表现为强化作用。由结合面接触刚度的变化幅度可以看出,对结合面接触刚度影响最为明显的是主轴转速,其次为径向铣削载荷,然后为轴向铣削载荷。

图3 径向铣削载荷和主轴转速对结合面刚度的影响Fig.3 Influence of radial milling load and spindle speed on joint surface stiffness

图4 轴向铣削载荷和主轴转速对结合面刚度的影响Fig.4 Influence of axial milling load and spindle speed on joint surface stiffness
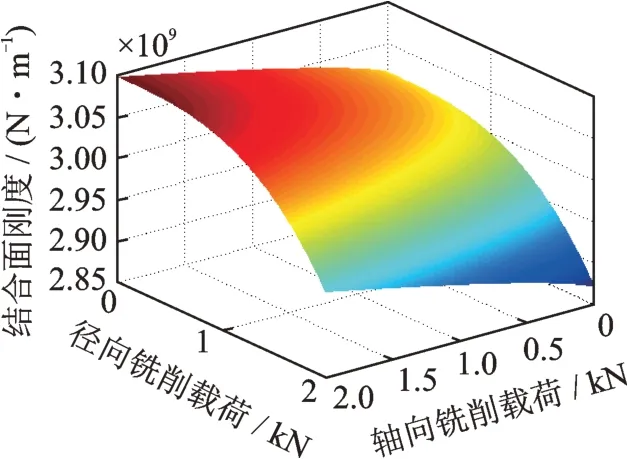
图5 轴向铣削载荷和径向铣削载荷对结合面刚度的影响Fig.5 Influence of axial milling load and radial milling load on joint surface stiffness
1.2 主轴-轴承结合面接触刚度
主轴系统中使用的轴承在铣削工况下,要同时受到轴向铣削载荷、径向铣削载荷以及主轴高速旋转状态下产生的离心力和陀螺力矩等影响,此时需要对其内圈和外圈进行平衡。轴承受载产生径向相对位移和轴向相对位移,轴承第t个滚动体的方位角表达式为
其中:z为轴承中滚动体的数目。
滚动体几何关系如图6 所示,根据其中的变形关系,分析获得轴承内外圈的位移平衡方程为
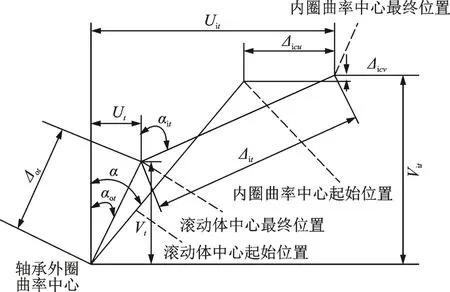
图6 滚动体几何关系Fig.6 Geometric relationship of rolling elements
其中:Uit,Vit分别为内外圈曲率中心轴向距和径向距。
根据赫兹理论得到接触载荷和内外圈接触变形位移之间的关系式,即
其中:Kit为内圈赫兹接触常数;Kot为外圈赫兹接触常数。
主轴系统运转过程中的滚动体受力分析如图7所示,此时轴承滚动体的受力平衡方程为

图7 滚动体受力分析Fig.7 Force analysis of rolling elements
其中:Qit,Qot为滚动体与内外圈接触载荷;αit,αot为滚动体与内外圈接触角;Mgt为陀螺力矩;Fct为离心力;D为滚动体直径。
式(8)中,若应用外圈控制理论,则λit=0,λot=2;若应用内圈控制理论,则λit=1,λot=1。当应用的控制理论不同时,滚动体所承受的离心力和陀螺力矩存在一定差异,但结果差异量微小,结合面刚度特性变化基本相同。
对轴承进行整体的受力分析如下
其中:Ri为内滚道曲率中心圆半径;ri为内滚道半径;Frx为前、后主轴-轴承结合面受到的径向载荷(见图1),x=1,2。
联立式(7)~(10),应用Newton-Raphson 迭代法求解得到Ut,Vt,δit和δot的结果。通过坐标变换获得轴承内圈不同自由度的受力平衡式,并累计所有滚动体与内外圈接触力,所得合力对位移求导,得到主轴-轴承结合面接触刚度矩阵。
根据理论模型运算结果,得到轴向铣削载荷、径向铣削载荷及主轴转速对主轴-轴承结合面接触刚度影响分别如图8~10 所示。可以看出:当轴向铣削载荷增加时,主轴-轴承结合面接触刚度缓慢升高,在大约800 N 后逐渐稳定;当径向铣削载荷增加时,主轴-轴承结合面接触刚度逐渐降低,在大约500 N 以后加速下降;当主轴转速增加时,主轴-轴承结合面的接触刚度随之降低,且转速越大,降低越明显。这是因为转速增大,离心力和陀螺力矩随之改变,导致轴承外圈接触载荷逐渐增大,主轴-轴承结合面接触刚度随之发生变化。
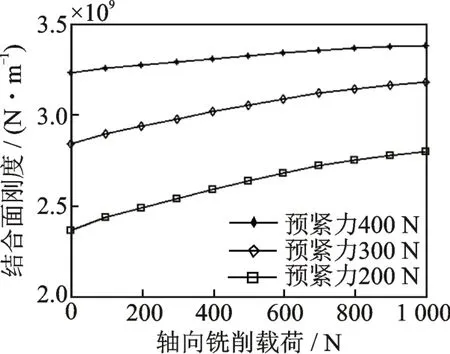
图8 轴向铣削载荷对主轴-轴承结合面接触刚度影响Fig.8 Influence of axial milling load on contact stiffness of the spindle-bearing interface

图9 径向铣削载荷对主轴-轴承结合面接触刚度影响Fig.9 Influence of radial milling load on contact stiffness of the spindle-bearing interface
1.3 铣削工况下主轴系统动力学模型
主轴系统有限元模型如图11 所示,其中主轴、刀柄和铣刀等部件等效为Timoshenko 梁单元,结合面等效为弹簧阻尼单元。将主轴系统部件质量矩阵M、刚度矩阵K、阻尼矩阵C和主轴-刀柄-铣刀结合面刚度矩阵Kc、阻尼矩阵Cc、主轴-轴承结合面刚度矩阵Kw、阻尼矩阵Cw耦合,边界条件主要应用弹性约束,主轴前端法兰盘部分与机床主轴箱之间的联接作用弹性支承模拟,获得理论模型为

图11 主轴系统有限元模型Fig.11 Finite element model of spindle system
其中:F为力向量。
主轴系统阻尼矩阵采用比例阻尼确定
其中:α1,β1为比例系数[8-9]。
应用子空间迭代法求解获取主轴系统动力学模型数值结果,得到铣削工况下的主轴系统的固有频率和频响函数。
2 铣削工况下主轴系统模型验证
采用一种铣削工况下的数控机床主轴系统动态测试方法来验证所建立模型的正确性,该方法以铣削载荷信号作为激励,主轴系统铣削振动加速度信号作为响应,通过测试数据分析与处理,获得铣削工况下主轴系统的动态特性[19-20]。这种方法一般要求激励信号为随机信号,而实际铣削载荷信号中必然含有周期信号,因此需剔除铣削载荷信号中周期信号引起的振动响应谐频。
由铣削载荷信号和振动响应信号获得铣削工况下系统频响函数,采用奇异谱分析法对该频响函数进行奇异谱分析,选择奇异值分量占比最大者作为主成分,将频响函数进行重构后,该阶奇异值对应的特征分量即可描述频响函数的频率固有特性,达到消除谐频及干扰信号影响的效果,进而提取动力学信息,获取铣削工况下的机床主轴系统的模态参数。奇异谱分析法具体过程如下。
1) 建立轨迹矩阵。实验采集原数据长为N,滑动窗口长为LP,KP=N-LP+1,采用列分割方式对轨迹矩阵进行处理,第ip列数据为ip~Lp+ip-1,其中ip为列数,ip=1,2,…,KP,轨迹矩阵为
2) 奇异值分解。主要包括以下步骤:①计算XXT的特征值λi(i=1,2,…,N;λ1>λ2>…>λN)和特征向量ui;②计算右奇异向量原轨迹矩阵可表示为
3) 分组。主要是将有效数据与要剔除的谐频进行分组,选取前r个奇异值作为主成分进行后续重构等处理。
4) 重构信号。依据上述分组结果将对应的奇异向量进行重构
实验使用VDL-1000E 型数控加工中心,使用戴杰二刃整体硬质合金球头铣刀,加工工件Cr12MoV(HRC58),利用Kistler9257B 测力仪测试铣削载荷信号,利用PCB 加速度传感器测试铣削振动响应信号,灵敏度为10.42 mV/g。实验设备如图12 所示。

图12 实验设备Fig.12 Experimental setup
通过3 组铣削实验进行验证,参考制造企业实际铣削工艺,确定铣削实验工艺参数如表1 所示。
表1 铣削实验工艺参数Tab.1 Technological parameters of milling experiment
实验与仿真对比分析如图13 所示,铣削状态下的主轴系统频响函数比静止状态下更贴近实验结果。主轴系统固有频率对比如表2 所示,由表2 可以看出,铣削状态下的主轴系统固有频率与实验结果之间误差明显低于静止状态下主轴系统固有频率的误差。3 组工艺参数铣削过程中,系统前3 阶固有频率分别降低11.45%,10.88%和11.72%,铣削状态下的仿真结果与实验结果之间的误差比静止状态下的误差平均降低11.35%,证明铣削工况下主轴系统动力学模型能更准确地反映铣削状态下主轴系统的动态特性,可以作为铣削状态下主轴系统动态特性预测模型。

表2 主轴系统固有频率对比Tab.2 Comparison of natural frequency of spindle system

图13 实验与仿真对比分析Fig.13 Comparative analysis of experiment and simulation
3 铣削工况下主轴系统动态特性分析
3.1 铣削工况下的主轴系统固有频率分析
铣削工况下,考虑径向、轴向及主轴转速的主轴系统固有频率分别如图14~16 所示。由图可知:当径向铣削载荷由0 增加到1 kN,由于径向铣削载荷对结合面刚度特征的弱化效应,1 阶、2 阶和3 阶固有频率分别降低了5.45%,5.37%和6.33%;当轴向铣削载荷由0 增加到1 kN,由于轴向铣削载荷对结合面刚度特征的强化效应,1 阶、2 阶和3 阶固有频率分别升高了4.28%,3.78% 和1.85%;当主轴转速由0 增加到12 kr/min 时,由于离心力和陀螺力矩对结合面刚度特征的弱化效应,1 阶、2 阶和3 阶固有频率分别降低了16.02%,7.35% 和5.54%。可以看出,对主轴系统固有特性影响最为明显是主轴转速,其次为径向铣削载荷,然后为轴向铣削载荷。

图14 考虑径向铣削载荷的主轴系统固有频率Fig.14 Natural frequency of spindle system considering radial milling load

图15 考虑轴向铣削载荷的主轴系统固有频率Fig.15 Natural frequency of spindle system considering axial milling load

图16 考虑主轴转速的主轴系统固有频率Fig.16 Natural frequency of spindle system considering spindle speed
3.2 铣削工况下的主轴系统频响函数分析
考虑径向铣削载荷、轴向铣削载荷及主轴转速的频响函数分别如图17~19 所示。可以看出:径向铣削载荷增加时,各阶固有频率降低,且低阶固有频率振动幅值明显增加;轴向铣削载荷增加时,各阶固有频率略有增加,其中2 阶固有频率振幅明显下降;主轴转速增加时,各阶固有频率降低,主轴转速越大,降低速率越大,其中1 阶固有频率振幅略有下降,2 阶固有频率振幅明显升高。

图17 考虑径向铣削载荷的频响函数Fig.17 Frequency response function considering the radial milling load

图18 考虑轴向铣削载荷的频响函数Fig.18 Frequency response function considering the axial milling load

图19 考虑主轴转速的频响函数Fig.19 Frequency response function considering the spindle speed
4 结 论
1) 建立铣削工况下的主轴结合面解析模型并分析其刚度特征,结果表明:随着主轴转速的增加,结合面接触刚度下降,较高速时下降更明显,即离心力对结合面接触刚度有明显弱化作用;径向铣削载荷对结合面接触刚度同样表现为弱化作用;轴向铣削载荷对结合面接触刚度表现为强化作用。其中,影响最为明显的是主轴转速,其次为径向铣削载荷,然后为轴向铣削载荷。
2) 将结合面接触特性解析模型与主轴系统有限元动力学模型耦合,建立铣削工况下轴承-主轴-刀柄-铣刀系统的有限元动力学耦合模型,并利用一种铣削状态下主轴系统动力学测试方法,对理论模型进行实验验证,静止状态下对比铣削工况下的预测结果误差平均降低11.35%。
3) 转速会显著影响主轴系统固有频率和频响函数,铣削载荷也会对固有频率和频响函数产生不同程度的影响,主要体现在低阶模态。研究结果为铣削状态下主轴系统动态特性和铣削稳定性准确预测奠定理论基础,为保证铣削过程稳定和工件表面加工质量提供理论支持。

