玻璃微珠液滴碰撞分离过程数值研究

李慧玲, 胡晓磊, 余子寒, 谢能刚

(安徽工业大学 机械工程学院, 安徽 马鞍山 243032)

0 引 言

玻璃微珠是近年来发展起来的一种用途广泛、性能特殊的新型无机非金属材料．玻璃微珠具有强度高、流动性好、光学性能优异等显著特点,因此被广泛应用于军事、航空、建材及其他高科技领域作光反射材料、净化抛光材料、填充材料、载体材料等．随着科学技术的不断发展和用户对产品性能要求的不断提高,玻璃微珠的直径越来越小,范围可达到数微米到数百微米[1]．玻璃微珠的生产方法分为物理法和化学法,采用物理法制备玻璃微珠的技术发展较为成熟．生产中常用的固相玻璃粉末法就是一种物理法,该方法常将玻璃粉料和燃料喷入球化炉内,使玻璃粉末颗粒充分受热熔化,获得熔融的玻璃微珠液滴,在此过程中玻璃微珠液滴之间大多发生碰撞分离现象,但由于炉内温度过高,该微观运动过程难以捕捉[2]．

为准确预测玻璃微珠液滴碰撞过程,需要对玻璃微珠液滴碰撞过程进行数值模拟．液滴碰撞过程是一个涉及多尺度、非线性问题的复杂流动过程,对于一些时间和空间的微观信息,实验难以捕捉．与实验研究相比,数值模拟在流场及参数设置方面具有更大柔性．在此方面,夏盛勇等[3]采用流体体积(VOF)方法对直径为10～200 μm的三氧化二铝液滴碰撞过程进行了数值模拟,获得了反弹、大变形后聚合和自反分离等结果类型,研究了不同Weber数下的结果,并得到了它们之间的临界Weber数．Fostiropoulos等[4]研究了水乳化重油燃料爆炸液滴的碰撞行为,用3个VOF传输方程分离共存水液体和水蒸气流体界面,分析模拟结果,得到液滴破碎只发生在燃料-空气界面的一部分,类似于喷气的特征．尹强等[5]将VOF方法用于研究循环冷却系统中海水液滴碰撞过程,得到了聚合和自反分离两种结果类型及二者的临界Weber数,分析了流场结构、液滴直径和海水浓度对碰撞结果的影响．

Amani等[6]使用守恒的水平集(level set)方法模拟了所有体系中正面和偏离中心的二元液滴碰撞,介绍了一种新的薄层稳定方法来数值解析薄膜,并对每个案例进行了深入的能量分析,涵盖了广泛的碰撞范围,为碰撞过程提供了更深入的见解．Ashna等[7]采用LBM方法研究了液滴的蒸发过程,引入了有效表面张力测量蒸发速率对碰撞结果的影响,得到了其随Stefan数或Weber数增加而减少,随时间的增加而增加的规律．Liu等[8]通过将实验可视化与数值模拟相结合,研究了双乳化液滴的水动力剪驱动二元碰撞,发现了过渡和反转这两种典型碰撞运动,并得到了它们之间的决定影响因素．Zhang等[9]用分子动力学的方法研究了尺寸对二元碰撞纳米液滴动力学的影响,对不同直径液滴的拉伸因子、能量耗散和碰撞结果进行分析,得到了纳米尺度上原子相互作用引起的动能耗散对液滴分离的发生或其他方面有显著影响．

Li等[10]采用CLSVOF方法的数值模型,研究了空心液滴对干燥平面冲击的动力学和传热问题,比较了高空化气泡压力的空心液滴与连续致密液滴的动力学和传热特性,得到了液滴在这两种条件下的碰撞规律．Qian等[11]利用CLSVOF方法和自适应网格细化,对Newton液体和聚合物液体的碰撞行为进行了数值研究．对液滴的变形过程、内部流场和能量演化进行了详细分析,得到了二者在液滴碰撞过程中的不同之处,主要分析了聚合物液滴碰撞的一些变化特征．由上述文献可知,国内外对液滴碰撞机理的研究已然十分成熟．然而,截至目前,国内外尚未见公开发表针对玻璃微珠液滴碰撞物理规律及模型的研究．

鉴于对熔融玻璃微珠液滴碰撞过程实验观测的困难性,本文采用CLSVOF方法[12]开展两个相同尺寸玻璃微珠液滴对心碰撞的数值模拟．首先阐述了液滴碰撞的基本模型以及相关参数计算公式,随后建立了玻璃微珠碰撞过程数值模型和计算方法,采用建立的数值方法对Qian等[13]的实验开展数值验证,最后研究了玻璃微珠液滴对心碰撞分离的物理规律．

1 液滴碰撞基本模型

图1给出了两个相同尺寸液滴对心碰撞模型示意图,其中D0是液滴直径,v是液滴速度,L为两液滴的初始间距．计算区域为5D0×2.5D0．由于模型具有轴对称特性,本文采用二维轴对称计算条件,计算域底部为轴对称边界条件,其他三边均为压力出口,计算区域如图1所示．

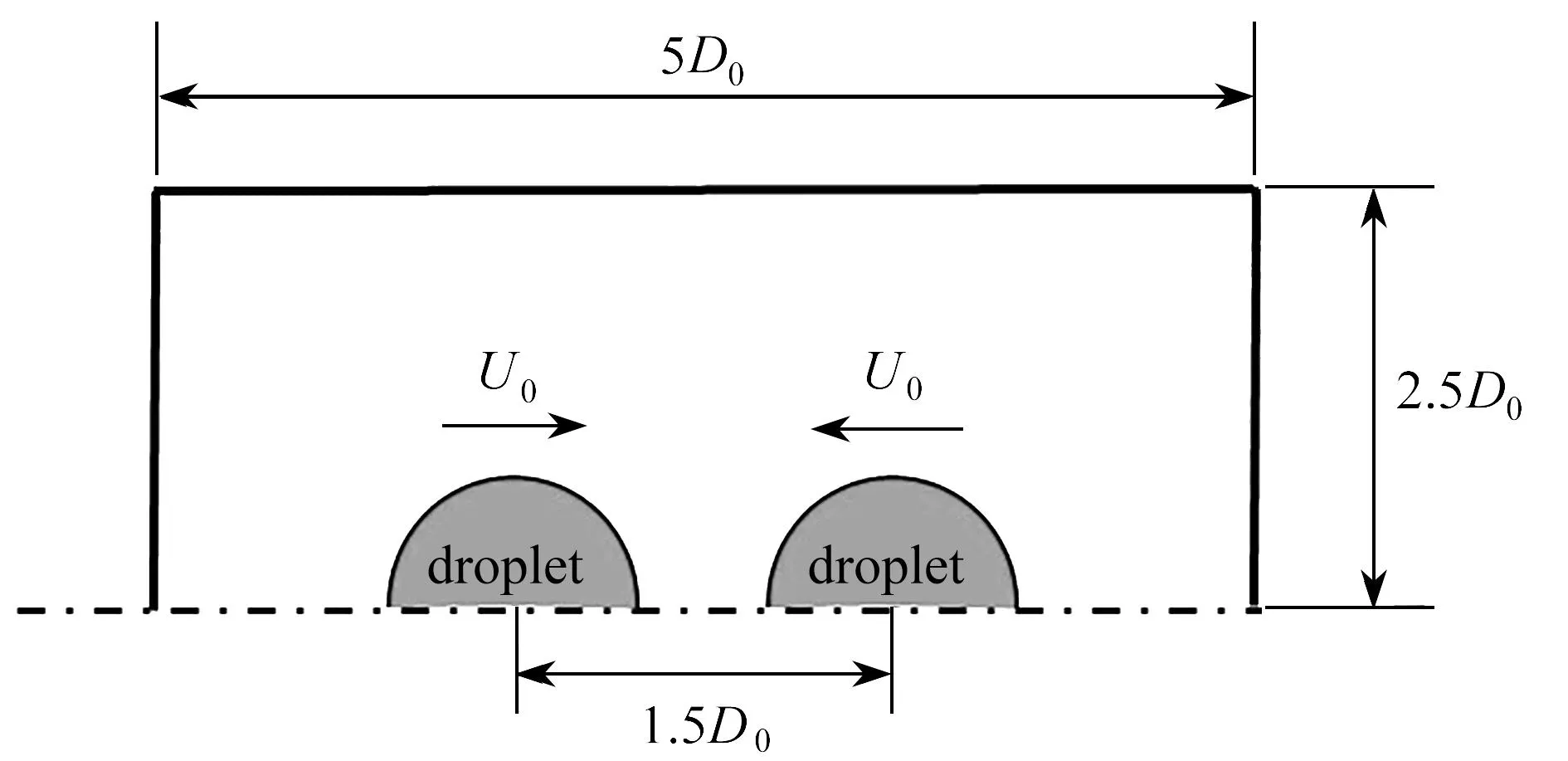
图1 物理模型Fig. 1 The physical model

2 数值计算方法

液滴碰撞是两相流问题,目前,两相界面的捕获方法主要有:VOF法[14]、水平集[15]以及 CLSVOF方法．VOF法难于计算相界面曲率,会导致解的振荡以及界面的陡峭变化被抹平．水平集法在计算时不可避免地引入数值耗散和舍入误差,造成封闭界面内流体质量损失,从而导致质量不守恒．VOF法和水平集法具有各自的优势和劣势,但是这两种方法的优、劣势正好可以互补．因此,Sussman等[16]提出使用VOF法和水平集法相耦合的方法,即CLSVOF方法进行相界面追踪,该方法能准确捕获相界面的同时,保证质量守恒．

对于流体力学问题,涉及到的基本控制方程如下所示:

∇·v=0,

(1)

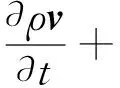
(2)

式中v为速度矢量,m/s2;p为流体压力,Pa;F为表面张力源项;g为重力加速度,m/s2;μ为流体动力黏度．CLSVOF方法在捕获两相界面时涉及到的水平集函数为

(3)

式中Ω1,Ω2分别是液相和气相,Γ为两相界面,L为区域内点到界面的距离．

通过引入Heaviside函数来使界面的密度和黏度光滑过渡:

(4)

式中a为1.5倍的最小网格尺寸．

式(2)的表面张力源项F为

F=σκ(φ)∇H(φ)n,

(5)

式中,σ是液相的表面张力系数,n是两相界面的法线,κ(φ)是两相界面的曲率．法线n和曲率κ(φ)的表达式如下:

(6)

(7)

光滑后的密度和黏度为

ρ(φ)=ρg+(ρl-ρg)H(φ),

(8)

μ(φ)=μg+(μl-μg)H(φ),

(9)

式中ρ(φ)为各相的平均密度,kg/m3;ρg为气相的密度,kg/m3;ρl为液相的密度,kg/m3;μ(φ)为各相的平均动力黏度,N·s/m2;μg为气相的动力黏度,N·s/m2;μl为液相的动力黏度,N·s/m2．

对于碰撞结果描述涉及到的Weber数和Reynolds数公式定义如下:

(10)

(11)

式中,ρ为液滴密度,kg/m3;d为液滴直径,m;u为液滴速度,m/s;σ为表面张力系数,N/m;μ为液滴动力黏度,N·s/m2．

采用PISO方法耦合求解速度场和压力场,时间项采用Euler方法进行离散,压力项采用PRESTO方法进行求解,动量方程采用二阶迎风格式进行求解,水平集函数采用一阶迎风格式离散求解．

3 数值算法的验证

为验证数值方法是否适合计算液滴碰撞及其可靠性,本文针对文献[13]正十四烷液滴在1 atm(1 atm=101 325 Pa)的常温氮气环境下的实验进行数值模拟验证计算,计算流体物性参数见表1．

针对文献[13]中图4(h)近对心碰撞工况开展了数值计算,计算结果如图2所示,其中实验结果为三维拍摄图．对比计算及实验结果可以看出,计算最终结果是自反分离,取得了与实验基本一致的液滴变形过程,只是在时刻上略微有所不同．

表1 正十四烷液滴的物理参数

(a) 实验结果[13] (b) 计算结果 (a) Experimental results[13] (b) Calculation results

4 计算结果及分析

4.1 玻璃微珠液滴及气相物性参数

玻璃微珠液滴的尺寸一般介于几微米到几百微米之间,本文选择两个尺寸相同的玻璃微珠液滴计算,直径均为20 μm．模拟中所采用的物性参数是参考彭寿等[2]研究玻璃微珠球化时所用的参数,如表2所示．

表2 玻璃微珠液滴的物理参数

4.2 玻璃微珠液滴对心碰撞数值研究

本文仅研究两个相同尺寸玻璃微珠液滴对心碰撞分离的规律特性．在Weber数为149的工况下,液滴碰撞分离形成了多个卫星液滴,但最终只有一个较大的卫星液滴保持稳定形态,因此选取它来进行玻璃微珠液滴碰撞分离的规律特性研究．通过对两玻璃微珠液滴碰撞过程中的形态变化、 能量变化、 中心处压力变化和关键时刻的速度矢量图以及压力云图的分析, 研究玻璃微珠液滴碰撞后发生分离的原因．模拟结果如图3所示．

图3为两相同尺寸玻璃微珠液滴碰撞后自反分离的计算结果．两液滴突破气膜后发生聚合,0.5 μs聚合后在表面张力的作用下发生径向伸展变形,形成片状射流;在2.0 μs时液滴径向拉伸到极限,之后液滴径向收缩,并同时向轴向伸展;在6.0 μs时,液滴轴向拉伸到极限,不再延展,但径向仍在不断收缩,形成液桥;在11.5 μs时液滴发生分离,液桥分裂形成3个卫星液滴,在表面张力的作用下,大卫星液滴两侧的小卫星液滴迅速与左右两个大液滴融合,最后形成两个完整的液滴．

图3 计算结果(We=149, Re=135.52, Ur=44 m/s)Fig. 3 Calculation results (We=149, Re=135.52, Ur=44 m/s)

4.2.1 玻璃微珠液滴对心碰撞过程中的能量变化

许多研究表明在液滴碰撞过程中,存在3种能量即液滴动能Ek、表面能Es和黏性耗散能Ev在发生变化[17-18]．为研究玻璃微珠液滴对心碰撞过程中的能量变化情况,本文对上述3种能量进行计算分析．液滴碰撞过程能量守恒可表示为

Ek0+Es0=Ekn+Esn+Ev,

(12)

式中Ek0,Es0分别是液滴初始动能和初始表面能;Ekn,Esn和Ev分别是液滴碰撞过程中的动能、表面能和黏性耗散能．初始状态下的动能和表面能计算公式如下:

(13)

Es0=σS=4πσR2,

(14)

式中ρ为液滴密度;R为液滴半径;v0=1/(2Ur),Ur为液滴碰撞的相对速度;σ为表面张力系数．

碰撞过程中的动能和表面能需要计算液滴的体积和表面积,由于模拟环境为二维平面,无法直接得到液滴的体积和表面积．为此本文使用当量半径Re,它是由现有的二维平面的液滴面积演化而来的．我们假设二维平面的液滴面积S为三维液滴的中心截面面积,并且把它等量成球的中心截面Se,则该球的半径即为当量半径Re,计算公式为

(15)

液滴碰撞过程中的动能计算公式为

(16)

式中v为液滴速度．

液滴碰撞过程中的表面能计算公式为

(17)

液滴碰撞过程中的黏性耗散能计算公式为

Ev=Ek0+Es0-Ekn-Esn．

(18)

由上述公式计算出各个时刻相应的能量,并将它们与初始总能量即Ek0+Es0相除进行无量纲化处理,得到We=149时玻璃微珠液滴碰撞分离过程的能量变化曲线,如图4所示．图中Es,Ek和Ev曲线分别代表表面能、动能和黏性耗散能的变化情况．从图中可以看出,在玻璃微珠液滴相互靠近,突破气膜阻力,碰撞后轴向收缩,径向拉伸的过程中,动能先迅速下降,在液滴即将拉伸到极限时,动能缓慢减小,在2.0 μs动能减小至零;由于液滴融合,表面积减小,表面能缓慢下降,在2.0 μs降到最小;由于动能和表面能减小,黏性耗散能持续增大,在2.0 μs增至最大．2.0～2.5 μs动能和表面能基本保持不变,这是因为液滴轴向继续收缩,径向变化不大,在2.5 μs轴向收缩到极限．2.5 μs后,液滴径向收缩,轴向拉伸,在4.0 μs径向收缩和轴向拉伸达到平衡,11.5 μs液滴发生分离,产生3个卫星液滴．在这个过程中,动能先增大,当径向收缩和轴向拉伸达到平衡时,动能增至最大,随后在表面张力的作用下,液滴径向收缩,轴向拉伸形成液桥,在二者的持续作用下,液桥逐渐变细,在12.0 μs被夹断,在此期间,动能缓慢减少至零．液滴在2.5 μs后,由于径向收缩、轴向拉伸,表面积增大,表面能逐渐增大,在6.0 μs液滴轴向拉伸到极限时增加到最大值．随后由于液滴径向不断收缩,液桥变细,导致表面能小幅减小．在液桥被夹断,形成3个大小不一的卫星液滴后,由于小卫星液滴和大液滴的融合,表面能发生小幅振荡,最后和初始表面能相当,符合VOF方法的质量守恒特征．黏性耗散能由于动能和表面能的增加,急剧下降,在液滴收缩拉伸达到平衡后缓慢增长．

通过上述分析可以得出,液滴动能是前期液滴发生碰撞融合的主要动力,在整个碰撞过程中对于液滴的收缩拉伸变化有着重要作用,在收缩拉伸过程中,动能会出现峰值．液滴在碰撞后径向拉伸过程表面能减小;在轴向拉伸至分离过程中,表面能先增大后减小,恢复至初始表面能水平．液滴碰撞过程中黏性耗散能变化受动能和表面能影响,但从最终结果来看,液滴初始动能绝大部分转化为黏性耗散能．由此可以看出,液滴碰撞过程中的分离结果受动能的起伏变化和表面能的变化的影响较大,在轴向拉伸前期,动能增大,表面能增大,为后面液滴拉伸分离提供了能量支持．

4.2.2 玻璃微珠液滴总压变化

玻璃微珠液滴在发生碰撞的过程中,其静压和动压都在发生变化,只分析其中一个都比较片面．而总压为两者之和,可以较为全面地反映液滴的压力变化规律．图5为两液滴碰撞过程液滴平均总压变化折线图．从图中可以看出, 两液滴从零时刻开始相互靠近,压缩气膜,液滴总压升高．0.5～2.0 μs为两液滴碰撞融合,并径向拉伸到极限的过程,液滴总压持续下降,在2.0 μs降至最低．2.0～4.0 μs为液滴径向收缩,轴向拉伸达到平衡的过程,液滴总压持续增大,在4.0 μs达到平衡时增至最大．4.0～6.0 μs为液滴径向收缩,轴向拉伸到极限的过程,液滴总压减小．6.0 μs之后,液滴轴向不再拉伸,径向仍在不断收缩,中间液桥部分形态变化均匀,因此液滴总压保持不变．在11.5 μs时,可以明显看出液桥形态发生变化,两端变细,液滴总压也忽然增大,这与末端夹断机制一致[19-20]．液桥断裂之后,小卫星液滴和大液滴发生融合,形成稳定形态的过程中,液滴总压降至稳定状态．

4.2.3 玻璃微珠压力云图和速度矢量图分析

从上述玻璃微珠液滴能量变化和总压变化分析可知,液滴碰撞分离过程有4个重要状态,即:2.0 μs径向拉伸到极限,4.0 μs径向收缩和轴向拉伸达到平衡状态,6.0 μs轴向拉伸到极限和11.5 μs液滴液桥夹断分离．下面对这4种状态的压力云图和速度矢量图进行分析．图6给出的是两相同尺寸玻璃微珠液滴发生碰撞2.0 μs时,即液滴径向拉伸到极限的速度矢量图(图6(a))(红色箭头代表液相速度矢量,蓝色箭头代表气相速度矢量,后同)和液滴内部压力云图(图6(b))．从液滴的速度矢量图可以看出液滴的速度分布上下对称,上方的液滴拉伸部分速度向上,上端部分速度向下扩散;外部的速度在液滴周围呈大小不一的漩涡扩散,总体趋势向上,但上端部分漩涡有向下压缩液滴的趋势．下方液滴速度分布和上方相同,但方向相反,具有很好的对称性．液滴拉伸部分向上下两侧扩散的速度矢量箭头密集,但两端的速度矢量箭头稀疏,这是由于哑铃形玻璃微珠液滴中间部分较细,其界面曲率κ较大,在此处的表面张力较大,即式(2)中的动力源项F较大,使此处产生指向液滴内部的较大速度．这也表示液滴径向拉伸已达到极限,没有持续拉伸的趋势了,与此时刻之后液滴的形态变化相符．此时的液滴形态呈哑铃形,液滴压力云图与之相符,且压力是从两端向中心逐渐减小,这和图5中此时刻的平均总压变化相符．

图4 玻璃微珠液滴碰撞分离过程能量变化曲线

(a) 速度矢量图 (b) 压力云图 (a) Velocity vectors (b) Pressure contours

图7为玻璃微珠液滴径向收缩和轴向拉伸达到平衡时刻4.0 μs的速度矢量图和内部压力云图．从图7(a)可以看出,此时液滴的速度大多集中在左右两端,并分别向两端扩散．液滴两端的速度矢量箭头明显比较密集,这是由于液滴形态呈铃铛形状,中间左右两端部分突出,其界面曲率κ就较大,则在此处的表面张力,即式(2)中的动力源项F也就越大,使此处液体的速度越大．图7(b)为玻璃微珠液滴压力云图,图中显示液滴压力从上下两端向中心逐渐增大,从中心向左右逐渐增大．液滴压力和速度的分布的共同作用促成了此刻的液滴形态．

图8为玻璃微珠液滴轴向拉伸到极限时刻6.0 μs的速度矢量图和内部压力云图．从图8(a)可以看出,此时液滴的速度分布均匀,并且从中间分别向左右两端扩散,具有良好的对称性．此时的液滴形态呈柱状,形态匀称,界面曲率κ没有明显变化,所以液滴速度分布均匀．在端部分布有速度漩涡,与液滴内部速度方向相反,阻碍液滴的轴向拉伸．图8(b)为玻璃微珠液滴压力云图,两端的压力比中部压力大,但两者相差不大．速度矢量图和压力云图都与液滴的形态变化特性相符．

(a) 速度矢量图 (b) 压力云图 (a) Velocity vectors (b) Pressure contours

(a) 速度矢量图 (b) 液滴内部压力云图 (a) Velocity vectors (b) Pressure contours

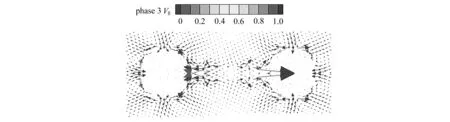
(a) 速度矢量图(a) Velocity vectors

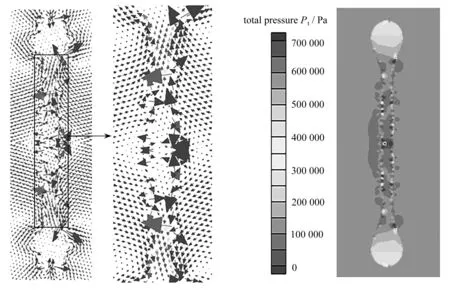
(b) 液桥局部放大速度矢量图 (c) 压力云图 (b) Partially amplified velocity vectors of the liquid bridge (c) Pressure contours

图9为两相同尺寸玻璃微珠液滴碰撞分离时刻11.5 μs的速度矢量图和压力云图．从图9(a)可以看出,此时液滴的速度大多集中在液桥部分,液滴形态呈哑铃状．图9(b)为图9(a)液桥部分速度矢量图的放大图,从中可以清晰地看出液桥部分的速度从两端向中部扩散,液桥外部末端靠近大液滴处有速度漩涡形成,速度从中心向两端扩散．图9(c)为玻璃微珠液滴压力云图,图中显示液滴压力都集中在液桥的部位,并从液桥中心向左右两边增大,导致末端压力最大．综合速度和压力分析可知两者的分布与液滴的末端夹断机制一致,这也是导致液滴碰撞分离的重要原因．

5 结 论

本文对玻璃微珠液滴碰撞分离过程进行了数值模拟研究,阐述了计算方法,并验证了计算方法可靠性,主要结论如下:

1) 在碰撞过程中,液滴的初始表面能和最终表面能相当,动能则绝大部分转化为黏性耗散能．

2) 在液滴轴向拉伸分离前期,动能增大、表面能增大为后期液滴分离供能,对玻璃微珠液滴碰撞后分离有着重要作用．

3) 通过对玻璃微珠液滴能量和平均总压变化的研究,得到了液滴碰撞分离过程有4种状态,即径向拉伸到极限、径向收缩和轴向拉伸达到平衡、轴向拉伸到极限和液滴液桥夹断分离．

4) 液滴的速度分布与液滴的形态密切相关,不规则的液滴形态导致界面曲率κ较大,以此影响界面的表面张力,使得不规则的液体部分产生较大的不同指向的速度分布．

5) 末端夹断机制是玻璃微珠液滴碰撞分离的主要原因．