高温高压模拟井筒应力分析与评价

侯永强, 纪 斌, 贾光政, 高 涵

(东北石油大学 机械科学与工程学院, 黑龙江 大庆 163318)

0 引 言

高温高压模拟井筒是用于模拟油田井下高温高压环境的实验装置．模拟井筒这类超高压容器在加温加压工作过程中会受到热应力与压应力的耦合作用,求解此类应力耦合作用所引起的强度问题,对指导机械、化工、航空航天和核反应堆工程等领域的超高压容器设计校核有重要意义．

针对复杂温度场下的热力耦合问题,国内外学者开展了大量的理论研究．通过解析法求解温度场分布,进而采用有限元法求解热应力和压应力耦合作用所引起的强度问题[1-6],计算过程中温度场与应力场独立计算,难以准确描述耦合效应,计算准确度相对较低．Almasi等[7]和杨阳等[8]使用解析和数值方法对热-力行为进行了研究．Manthena等[9]以Bessel函数的形式求解了瞬态二维传导方程及其相关热应力的解．耦合传热使得温度场分布复杂且非线性,难以用解析法准确求解,导致热应力无法准确求解．

模拟井筒加温加压实验时,内部充满液体并密封,为湍流自然对流传热过程．针对湍流求解过程中直接求解法(DNS)求解实际问题过程中计算量巨大,Reynolds时均方程法(RANS)求解精度不高的问题,Smagorinsky提出了大涡模拟(LES)方法．经过几十年的发展,大涡模拟已经被实验证明能够较准确地求解湍流自然对流传热[10-14],降低对计算机资源的苛刻要求,与直接求解法相比,减少了计算的工作量．

由于湍流自然对流传热数学模型的N-S方程的非线性特性,它的求解十分困难,需要通过数值方法进行求解．SIMPLE系列算法求解非稳态N-S方程计算量大,效率不高．文献[15-17]提出了投影法求解不可压缩黏性流体的N-S方程,以提高数值求解的效率．

综上所述,需要研究基于耦合传热温度场,以求解计算热应力的数学模型与数值求解方法．本文在此基础上准确求解模拟了井筒的热应力、压应力和耦合应力的分布规律,为模拟井筒这类高温高压容器的设计校核提供了理论方法．

1 模拟井筒实验装置

图1为模拟井筒加温装置,其中:①为风机,②为进风阀,③为内循环阀,④为冷却阀,⑤为风循环管道,⑥为井式加热炉,⑦、⑪为温度传感器,⑧为模拟井筒,⑨为加热电阻丝,⑩为炉衬．加温装置采用空气间接加热的包覆式井式电加热炉,为模拟井筒提供均匀稳定的高温试验环境．实验装置工作时,井式加热炉对模拟井筒外壁进行加热,超高压加压系统对模拟井筒内部加压,模拟井筒承受高温和高压作用．

图1 加温装置结构Fig. 1 The heating device structure

2 模拟井筒力学与热学物理模型

模拟井筒外半径rb=0.355 m,内半径ra=0.175 m,高度为3.534 m,腔高度为2.50 m,rb/ra≈2.03(当rb/ra>1.2时为厚壁圆筒),模拟井筒为轴对称厚壁圆筒．模拟井筒在理想状态下材质均匀、形状规整,且在三维空间内的形变也是对称且统一的,可以不考虑其轴向弯曲．在柱坐标系下采用位移法求解其轴对称非稳态温度分布下的金属热应力．模拟井筒金属厚壁材料为均匀的各向同性弹性体,加热过程中变形很小,发生变形的速率很慢,因而惯性力可以忽略,可以应用线性热弹性理论分析加热过程的热应力．加温加压过程中模拟井筒内部充满流体,井筒上下端面采取保温措施,可认为是绝热面,竖直外壁面为高温面．模拟井筒加热温度场径向对称,同时内部流体在重力场的作用下产生浮升力而形成自然对流,模拟井筒的导热模型可用二维模型来描述．图2为非定常高温高压模拟井筒热学与力学物理模型．

图2 非定常高温高压模拟井筒热学与力学物理模型Fig. 2 The unsteady thermal and mechanical physical model diagram for the high-temperature high-pressure wellbore hole simulator

2.1 热应力物理方程

在柱坐标系下模拟井筒厚壁的温度分布周向对称,温度的变化与轴向角度θ无关,即温度分布是只与半径r、高度z和时间t相关的函数T=T(r,z,t)．于是,周向位移uθ=0、径向位移ur和轴向位移uz都只是半径r和高度z的函数．由于温度T的变化,模拟井筒金属厚壁内各点的微小形变如果不受到约束,将发生线应变βT,β为模拟井筒金属厚壁的线膨胀系数．金属厚壁为各向同性体,线膨胀系数β不随方向变化,因此这种线应变在所有方向均相同,因而这个过程中无切应变．模拟井筒金属厚壁受到外在约束和其体内各部分之间相互约束,线膨胀形变并不能够自由发生,因此产生热应力,同时由于金属厚壁的弹性热应力将引起附加的形变．在变温的情况下弹性体的应变由两部分叠加而成: ① 热应变分量βT; ② 在热膨胀时由于弹性体内各部分之间的相互约束而引起的力学应变,它们和热应力之间服从Hooke定律．根据Duhamel-Neumann法则,考虑热应变的应力和应变在柱坐标下的关系为

(1)

(2)

(3)

γrθ=0,

(4)

γθz=0,

(5)

(6)

根据式(1)—(6)得出柱坐标下模拟井筒厚壁的热应力为

(7)

(8)

(9)

式中,σr为模拟井筒径向热应力,MPa;σθ为模拟井筒周向热应力,MPa;σz为模拟井筒轴向热应力,MPa;r为模拟井筒任意点的半径,m．

2.2 压应力物理方程

模拟井筒内部充满高压流体,圆筒形金属厚壁受到对称于中心轴的均匀内压与均匀外压(大气压)作用,其受力可以等效为平面轴对称问题．采用位移法求解,取位移分量u为基本未知函数,利用只包含应力分量的微分方程和边界条件求出位移分量,再利用几何方程求出应变分量,从而应用物理方程求出应力分量为

(10)

(11)

式中,pi为模拟井筒承受的内压,MPa;p0为模拟井筒承受的外压,MPa;Ri为模拟井筒承受的内径,m;R0为模拟井筒承受的外径,m;pr为模拟井筒径向压应力,MPa;σpθ为模拟井筒周向压应力,MPa．

2.3 模拟井筒大涡模拟温度场控制方程

大涡模拟通过将柱坐标系下模拟井筒耦合传热N-S方程进行滤波,即将变量划分成大尺度变量与小尺度变量．滤波后流体与固体区域统一的二维非稳态模拟井筒耦合传热控制方程为

(12)

(13)

(14)

(15)

μeff=μ+μt,

(16)

λeff的计算公式为

λeff=λ+ρcpαt,

(17)

μ为初始设定的流场涡黏度值,Pa·s;μt为亚格子涡黏系数,Pa·s;λ为初始设定的导热系数,W/(m·K);αt为亚格子涡扩散系数,m2/s．

大涡模拟亚格子涡黏系数采用Smagorinsky-Lilly模型,计算公式为

(18)

式中,Ls为亚格子混合长度,其定义式为

Ls=min(kd,Cs,Δ),

(19)

(20)

3 数值求解方法

3.1 温度场控制方程的离散

应用有限差分法对模拟井筒大涡模拟温度场的控制方程式(12)—(15)进行离散,控制方程采用交错网格进行离散,黏性项采用Crank-Nicholson 格式离散,对流项采用Adams-Bashforth格式离散得

(21)

(22)

(23)

(24)

以上各式中差分算子的定义为

Dr(*)i, j=((*)i+1/2, j- (*)i-1/2, j)/Δr,Dz(*)i, j=((*)i+1/2, j- (*)i-1/2, j)/Δz,

(*)i+1/2, j=((*)i+1, j+ (*)i, j)/2, (*)i, j+1/2=((*)i, j+1+(*)i, j)/2,

Lh(*)i, j= ((*)i+1, j-2(*)i, j+ (*)i-1, j)/Δr2+((*)i, j+1- 2(*)i, j+ (*)i, j-1)/Δz2,

Lm(*)i, j= ((*)i+1, j- (*)i-1, j)/(2Δr),

(*)表示离散变量,i,j分别表示r,z方向的单位向量．

3.2 投影法求解温度场控制方程

投影法求解温度场物理方程步骤如下:

(25)

(26)

把式(23)分解为下列两式:

(27)

(28)

第二步 压力修正步．将离散的动量方程式(26)和(28)代入离散的连续性方程(21)中,该方法可保证连续性方程严格满足．经整理得到离散的压力Poisson方程为

(29)

式中

(30)

式中,m为迭代次数;ω为松弛因子,ω>1时为超松弛迭代．

3.3 虚拟密度法求解流固耦合传热

3.4 非定常热应力数值求解方法

(31)

(32)

(33)

式(31)—(33)中的积分项采用梯形法数值积分求解．

(34)

(35)

(36)

3.5 压应力数值求解方法

压应力数值求解,采用与求解热应力相同的离散化节点划分方法,即离散化为相同的i个半径长度ri．压应力与热应力在空间维度有对应的离散单元,实现压应力与热应力的精确耦合计算．模拟井筒加温加压实验过程中压力保持恒定,为定常压应力,因此在时间维度不需要进行离散化．空间离散化的径向压应力和周向压应力为

(37)

(38)

4 应力的耦合与强度准则

根据应力叠加原理,应力耦合为热应力与压应力的和,热应力与压应力在半径r方向按照相同的网格离散方式进行离散,其离散化的非定常应力耦合计算公式为

(39)

(40)

(41)

根据von Mises第四强度理论,高温高压模拟井筒的等效应力为

(42)

(43)

(44)

5 求解结果及强度分析

5.1 力学参数及边界条件

模拟井筒为高温高压厚壁容器,由PcrNi3MoVA Ⅳ材料制造,表1为PcrNi3MoVA Ⅳ的力学参数．

模拟井筒加温加压过程的边界条件为:初始温度t0=25 ℃,上、下表面为绝热边界条件,竖直外壁面为高温面,加热温度400 ℃,中心轴为轴对称边界条件,边界位置如图2所示．压力修正方程的边界条件为Neumann边界条件,即∂p/∂n=0(n表示外法线)．模拟井筒放置在空气中,外部压力为大气压po=0.1 MPa,内部充满水,内部工作压力上限为220 MPa．根据建立的模拟井筒耦合传热,热应力和压应力数学模型及数值求解方法,编写计算程序进行数值求解．

表1 PcrNi3MoVA Ⅳ的力学参数

图3为模拟井筒中心高度1.77 m,不同时刻径向耦合温度分布．在加热过程中井筒金属厚壁部分的温度梯度变化趋势为先增加后降低．越靠近r=175 mm热耦合壁面处温度梯度大．沿径向方向模拟井筒腔体内壁面温度梯度较大．

5.2 热应力参数分析

图4—6为径向、周向和轴向非定常热应力在模拟井筒内壁面(r=175 mm)、模拟井筒厚壁内部中点(r=265 mm)和模拟井筒外壁面(r=355 mm)在不同时刻t的变化规律．

由图4可知,模拟井筒内壁面(r=175 mm)的径向非定常热应力随着加热时间的增加缓慢增加,模拟井筒厚壁内部中点(r=265 mm)与外壁面(r=355 mm)位置,加热初始时间段径向热应力较大,之后随着加热时间的增加热应力减小,并趋于定值．

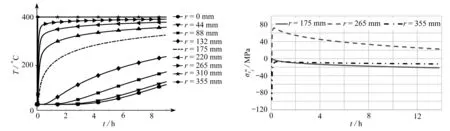
图3 不同时刻径向耦合温度分布

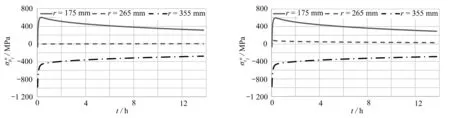
图5 周向非定常热应力的时间分布

由图5、6可知,周向与轴向的非定常热应力变化规律相同,在模拟井筒内壁面(r=175 mm)与外壁面(r=355 mm)处加热初始时间段周向与轴向热应力较大,之后随着加热时间的增加周向与轴向热应力减小,并趋于定值,模拟井筒厚壁内部中点(r=265 mm)处周向热应力趋于零．

图7—9为径向、周向和轴向热应力沿径向在不同时刻的变化规律．由图7—9可知,只考虑温度载荷时,径向热应力相较于周向和轴向的热应力小1个数量级;周向与轴向热应力沿径向由内到外按先正值后负值分布．

5.3 压应力参数分析

图10为只考虑模拟井筒内部流体压力作用时径向和周向压应力沿径向的变化规律．由图10可知,只考虑内压时,周向压应力为正值(拉应力),径向压应力为负值(压应力)．

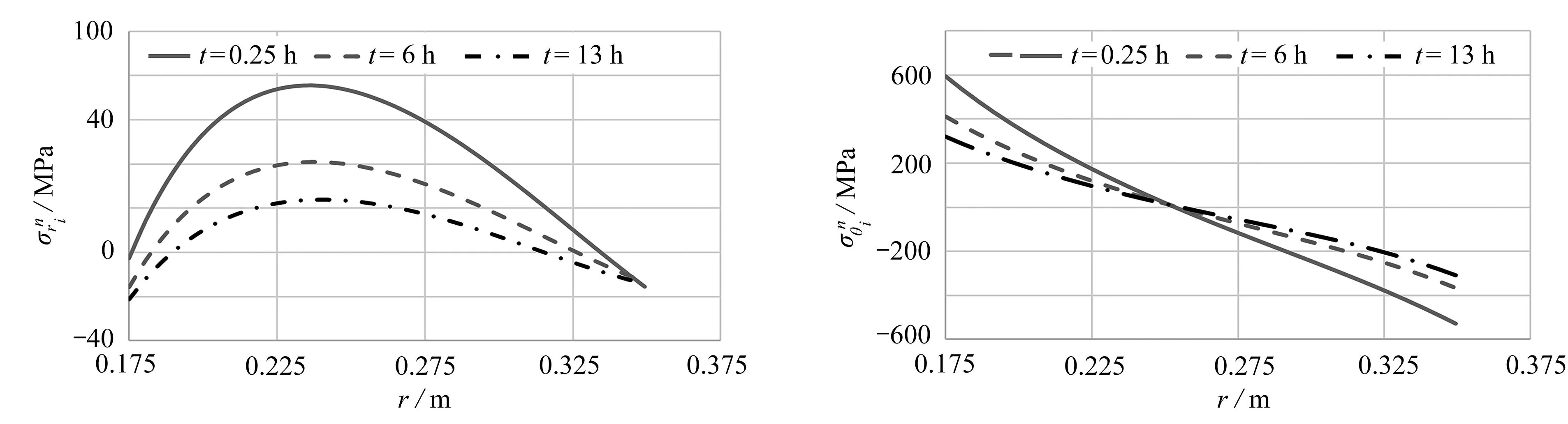
图7 径向非定常热应力沿半径的分布

图9 轴向非定常热应力沿半径的分布

5.4 等效应力求解结果参数分析

图11、12为等效热应力和等效应力耦合在厚壁井筒内壁面(r=175 mm)、厚壁井筒厚壁内部中点(r=265 mm)和厚壁井筒外壁面(r=355 mm)处在不同时刻t的变化规律．非定常等效热应力与等效应力耦合随着加热时间的增长,其值先增加到最大值,之后逐渐减小．

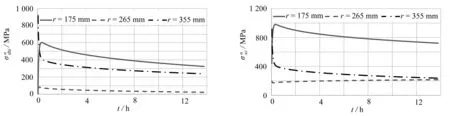
图11 非定常等效热应力沿径向的时间分布

5.5 模拟井筒的设计校核

图13为加温加压条件下,模拟井筒不同壁厚与等效应力最大值的关系．随着模拟井筒壁厚的增加,等效热应力最大值增大,等效压应力的最大值减小,等效应力耦合最大值基本保持不变．壁厚越大,模拟井筒的结构强度越大,因此最大等效压应力值越小．但随着壁厚的增加,模拟井筒在加热过程中,其金属厚壁的温度梯度会增加,因此最大等效热应力值增大．等效应力耦合为等效压应力与等效热应力的耦合作用结果, 在设计壁厚较大时(0.12～0.2 m)时, 壁厚发生变化时等效应力耦合最大值的变化率较小．在设计壁厚较小时(0.04～0.12 m),壁厚发生变化时等效应力耦合最大值的变化率较大．模拟井筒壁厚与最大等效压应力、等效热应力和等效应力耦合为非线性关系．因此在模拟井筒的设计过程中要综合考虑等效热应力,等效压应力和等效应力耦合的大小,三者均需满足强度要求．

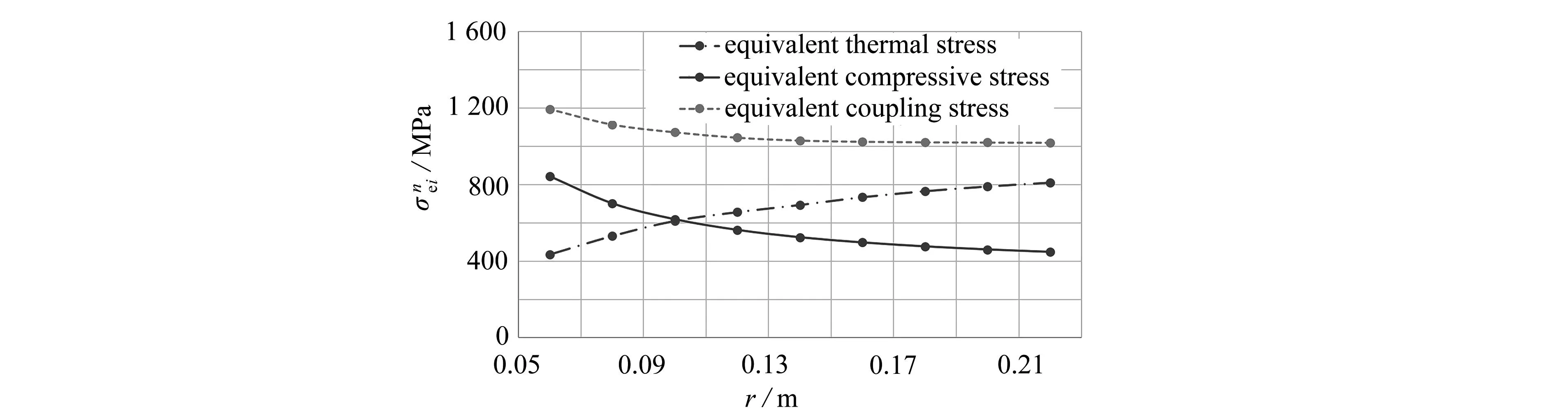
图13 模拟井筒壁厚与等效应力关系Fig. 13 The relationship between the wall thickness and the equivalent stress in the wellbore hole simulator

模拟井筒为超高压容器,根据《超高压容器》(GB/T34019—2017)的规定[18],理想弹塑性模型的屈服强度取材料在设计温度下屈服强度的0.9倍,屈服强度与等效压应力的比不小于2.20．设计模拟井筒的技术参数为:井筒壁厚为0.18 m,最高加热温度为400 ℃,最高工作压力为220 MPa．应用建立的模拟井筒热应力与压应力数学模型与数值求解方法进行理论分析计算,计算结果为等效应力耦合计算结果为1 022 MPa,最大等效压应力为477 MPa,等效热应力为766 MPa．模拟井筒PcrNi3MoVA Ⅳ材料在设计温度400 ℃下屈服强度为1 150 MPa,设计技术参数下等效应力耦合计算结果为1 022 MPa,小于0.9倍的屈服强度1 035 MPa,屈服强度与等效压应力的比为2.30,均满足标准规定．屈服强度与等效热应力的比为1.50,满足材料的强度要求．设计的最小壁厚为0.18 m,模拟井筒能够在温度400 ℃、工作压力220 MPa的参数下安全工作．

6 模拟井筒加温加压实验

通过模拟井筒加温加压实验,对建立的热力学数学模型与数值求解方法的数值求解结果的正确性进行实验验证．图14为模拟井筒加温装置,通过安装在井式电加热炉炉膛内及模拟井筒内部的热电偶传感器,实时测试炉膛内与模拟井筒内部流体的温度．图15为加压液控系统及加压泵,通过安装在模拟井筒加压液控系统的压力传感器,实时测试加压液体的压力．

图16为加温加压实验曲线,在实验过程中,模拟井筒通过井式电加热炉进行加热升温,炉温达到400 ℃后,保持炉温400 ℃加热．模拟井筒通过加压液控系统进行升压,模拟井筒内部压力达到220 MPa后开始保压,保压约15 h后开始卸荷,并停止加热降温．保压期间最高压力为222.47 MPa,最低压力为219.16 MPa．

模拟井筒安装有温度传感器,图1中的温度传感器⑪通过模拟井筒的下端接口插入其内部,测试模拟井筒腔高度为0.22 m,径向位置为r=0.12 m处内部流体的温度．实验与计算升温曲线如图17所示,升温过程的计算值与实验测试值的最大误差绝对值为4.79 ℃,计算结果与实验测试数据基本一致．图18给出了计算升温曲线相对实验升温曲线的相对误差,初始加热时间段0～2 h内相对误差最大,相对误差绝对值最大值为4.18%．随着加热时间的增加,相对误差不断减小,相对误差绝对值在2.5%以内．验证了建立的模拟井筒大涡模拟温度场数学模型及投影法求解流固耦合传热过程的准确性．

实验结果表明,在最高400 ℃的加热环境与内部加压最高220 MPa的实验参数条件下,设计最小壁厚为0.18 m的模拟井筒,能够安全且无泄漏的工作．通过加温加压实验,验证了建立的模拟井筒热应力与压应力数学模型与数值求解方法的正确性．

图14 模拟井筒加温装置Fig. 14 The wellbore hole simulator heating device

图15 加压液控系统及加压泵Fig. 15 The pressurized hydraulic control system and the pressure pump

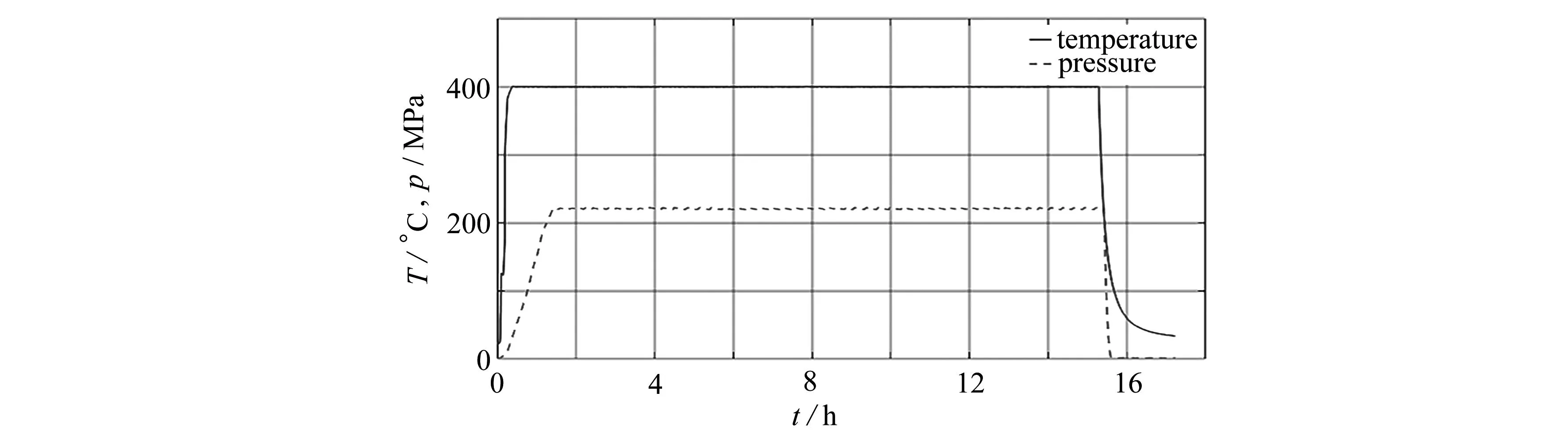
图16 加温加压实验曲线Fig. 16 Heating and pressurization experimental curves

图17 实验与计算升温曲线

7 结 论

本文基于热力学及大涡模拟理论,建立了模拟井筒大涡模拟温度场物理方程．基于热弹性力学理论建立了模拟井筒热应力物理方程．给出了投影法数值求解温度场控制方程的算法,梯形法数值积分求解热应力控制方程的算法,给出了温度场与应力控制方程的离散格式．通过虚拟密度法对流固耦合传热过程耦合求解,根据应力叠加原理对热应力与压应力耦合求解．对模拟井筒加温加压过程中的非稳态温度分布、热应力、压应力及其耦合作用进行了分析,对模拟井筒进行了校核计算．在最高400 ℃的加热环境下与内部加压最高220 MPa的实验参数条件下,设计最小壁厚为0.18 m的模拟井筒,能够安全且无泄漏的工作．通过模拟井筒加温加压实验,验证了所建立的模拟井筒这类高温高压容器热力学数学模型及数值求解结果的正确性,对指导高压容器设计有重要意义．