次表面分岔裂纹的力学行为

孙 奇, 吴金波, 江晓禹

(西南交通大学 力学与航空航天学院, 成都 610031)

0 引 言

随着现代工业的迅速发展,各种实际的工程问题离不开断裂理论的指导,以往研究中,多认为裂纹沿着其延长线进行扩展,却忽略了对裂纹二次断裂现象的研究．二次断裂现象是指裂纹沿直线扩展之后出现方向改变的现象,裂纹分岔就是一种重要的二次断裂现象．分岔裂纹常见于脆性材料、塑性较小的材料以及金属应力腐蚀问题中．通过对分岔裂纹的研究,可以初步预测裂纹是否会分岔、计算分支应力强度因子等,因其具有重要的工程意义,故长期受到断裂力学领域的关注．

从20世纪开始,国内外学者均对分岔裂纹做了大量工作,其中:Theocaris等[1]运用复势法研究了无限各向同性弹性板上对称分岔裂纹的平面问题,给出了分岔裂纹尖端的应力强度因子．Lam等[2]利用分布位错技术解决了圆形夹杂物与嵌入无限弹性介质中对称分岔裂纹之间的相互作用的问题,讨论了不同模量的夹杂对分岔裂纹扩展的影响．Yan[3]利用分布位错技术计算了无限大板中多条分岔裂纹相互作用的问题,给出了裂纹尖端附近的应力场．Yavuz等[4]把裂纹尖端位移不连续单元与恒位移不连续单元结合起来,为分岔裂纹的应力强度因子计算提供了一种更为精确的方法．Dahlan等[5]利用有限元方法研究了单轴牵引作用下二维板上的静态对称分支和非对称分岔裂纹．魏华建等[6]利用扩展有限元方法(XFEM)对分岔裂纹的非尖端破坏进行了讨论．Kornev等[7]采用有限元法求解双对称分岔裂纹,并使用Neuber Novozhilov型断裂准则和充分断裂准则计算得到了临界断裂参数．Chen等[8]在扩展有限元法的框架下,提出了一种研究复杂分岔裂纹扩展的增强扩展有限元方法．张端等[9]利用3D打印技术制作了不同形态的分岔裂纹,并研究了其在不同起裂荷载下的力学行为．

上述文献中的主要研究方法包括数值法、有限元方法、实验法、解析法,但其大多数研究的仅仅是在简单荷载下的分岔裂纹,且将裂纹所在平面简化为无穷大的情况,对于复杂荷载下的研究以及自由边界对分岔裂纹产生影响的研究仍有所不足．本文利用分布位错技术研究了半无限大平面内次表面分岔裂纹在复杂荷载下的力学行为．本文的主要研究内容为:根据等效应力强度因子判据,初步解释了裂纹产生分岔的原因;计算了分岔裂纹在不同埋深、荷载比值、分支长度比值、分岔角度下分支的应力强度因子;最后,还研究了多分支分岔裂纹的情况,其结果与有限元对照良好．此外,分布位错技术相较于有限元,略去了每次模型改变后繁琐的网格划分工作,只需要改变裂纹的位置参数便可进行计算,是一种便捷的研究分岔裂纹的数值方法．

1 原 理

1.1 问题描述

本文欲用理论方法(分布位错技术)研究分岔裂纹,重点是求解分支尖端的应力强度因子,由此讨论不同工况下分岔裂纹的力学行为．在图1中考虑将分岔裂纹建模为三条相交的直裂纹,分别表示为裂纹1(即主裂纹AD)、2(即DB裂纹分支)、3(即DE裂纹分支)．a,b,c分别表示主裂纹1、分支裂纹2、分支裂纹3的裂纹半长;d表示主裂纹中心到自由边界的距离;θB,θE分别表示分支裂纹2、3延长线与主裂纹延长线的夹角;A,B,E(为了应力强度因子表达式与断裂韧性有所区别)表示分岔裂纹尖端;D表示分岔点．

1.2 叠加原理

基于Bueckner定理[10],将主问题分解成两个子问题:子问题1,无裂纹时,外载在半无限弹性平面内产生应力的问题;子问题2,无外载时,半无限弹性平面内裂纹区域的刃位错产生应力的问题．最后根据裂纹面应力条件,将以上两个子问题联立求解．

1.3 建立位错密度积分方程

在半无限大板中由位错引起的应力分量由下式给出[10-11]:

(1)

其中κ是Kolosov常数,平面应变时κ=3-4ν,平面应力时κ=(3-ν)/(1+ν);ν是Poisson比;μ是剪切模量;bx和by代表Burgers矢量在x,y方向上的分量;Gxij和Gyij是位错影响函数,第一个下标表示Burgers矢量,后两个下标表示应力分量,其表达式可参考文献[11]．为了方便在局部坐标系下进行计算,需要进行以下坐标变换:

(2)

(3)

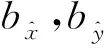
(4)

图1 复杂荷载下的半无限平面分岔裂纹Fig. 1 The semi infinite plane bifurcating crack under complex loads

在后续的计算中只需要变化ξ,x,y,θ,θ1,就可以得到由任意局部坐标系上的位错在任意局部坐标系上所产生的应力分量．以裂纹1对裂纹2的影响函数作为例子进行解释,如图2所示,其中红色图形代表刃型位错列．只需进行以下替换:ξ=ξ1,x=x2cos(θB)+d+a,y=x2sin(θB),θ=0,θ1=θB即可得到．其中ξ1是裂纹1上位错的全局横坐标;x是裂纹2的全局横坐标,y是裂纹2的全局纵坐标减去裂纹1的位错全局纵坐标;θ,θB分别代表裂纹1和裂纹2坐标系的偏转角;其余影响函数可用类似方法获得．

图2 坐标变换示意图Fig. 2 Schematic diagram of coordinate transformation

现在基于分布位错技术,将每条裂纹视为未知的连续分布的刃位错[11],表示为Bl(ξk),其中l=1,2分别代表x,y方向上的位错,ξk代表第k条裂纹分布位错的局部坐标(k=1,2,3)．因此,对于每一条裂纹而言,通过叠加包括自己在内的其他裂纹位错所产生的应力分量与外载荷产生的应力分量,并结合裂纹面的无牵引条件,可以得到

(5)

2 奇异积分方程的数值解

采用基于Gauss-Chebychev求积方法[12]的数值技术来求解积分方程组(5),首先需要对积分区域进行归一化处理:

(6)

其中

(7)

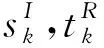
(8)

将方程(6)、(7)、(8)代入方程(5),得到离散化的方程:

(9)

方程(9)总共有6M-6个线性方程,但是总共需要求解6M个未知数,因此需要额外补充6个方程．所谓的封闭或者单值条件[12]提供了额外的两个方程式,这两个方程表示次表面分岔裂纹在x与y方向上的净位错位均为零．ak代表第k条裂纹的半长,

(10)

由于主/分支裂纹交点 (图1中的点D)处的奇异性小于1/2,文献[2]将分岔点处的应力强度因子处理为0,其实际可用的方程个数为6个．文献[2]经过比对不同的方程所产生的结果,选出了其中最佳的4个额外方程如下:

(11)

其中φl(sk=±1)可以通过文献[12]中的方法进行插值得到．至此,未知数个数与所需方程数相等,方程(9)可以得到解答．裂纹尖端的应力强度因子由φl(tk=±1)推出,例如尖端E的应力强度因子表示为

(12)

3 结 果 验 证

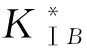
如图3所示,对比本文理论计算的结果与已有文献的结果,发现本文的理论计算结果与文献计算结果相差无几,足以说明本文理论模型的正确性,可以用于后续的计算．

图3 非对称分岔裂纹的计算结果对照图Fig. 3 Comparison of calculation results of asymmetric bifurcating crack

4 结果与分析

4.1 分岔裂纹产生的原因及过程

文献[14]研究发现,如果根据最大周向拉应力准则判断裂纹扩展角度,其预测的裂纹扩展角度变化过于剧烈,这与真实的实验结果及事实不符．因此采用文献[14]中的方法:如图4所示,将裂纹沿各个不同的方向扩展b=0.1a,计算裂纹在不同方向上的等效应力强度因子Keff=KⅠ+|KⅡ|,将其最大值所在的角度视为裂纹下一步的扩展角度．参数设置如下:荷载τ/σ=0.1,d/a=1.5．从图4中可以看出,Keff在-35°和20°时均出现了峰值,这说明裂纹在-35°和20°都容易发生扩展,从而导致出现分岔的情况．

4.2 埋入深度d/a对和的影响

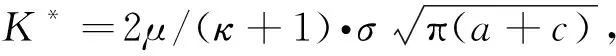
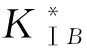
图4 不同角度下的等效应力强度因子及裂纹分岔示意图Fig. 4 Schematic diagram of the equivalent stress intensity factor and the crack bifurcation at different angles

图5 埋置深度对归一化应力强度因子的影响Fig. 5 Effects of burial depths on normalized stress intensity factors

4.3 荷载比值τ/σ对和的影响

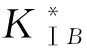
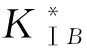
图6 荷载比值对归一化应力强度因子的影响Fig. 6 Effects of load ratios on normalized stress intensity factors

4.4 分支长度比值b/c对和的影响

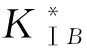
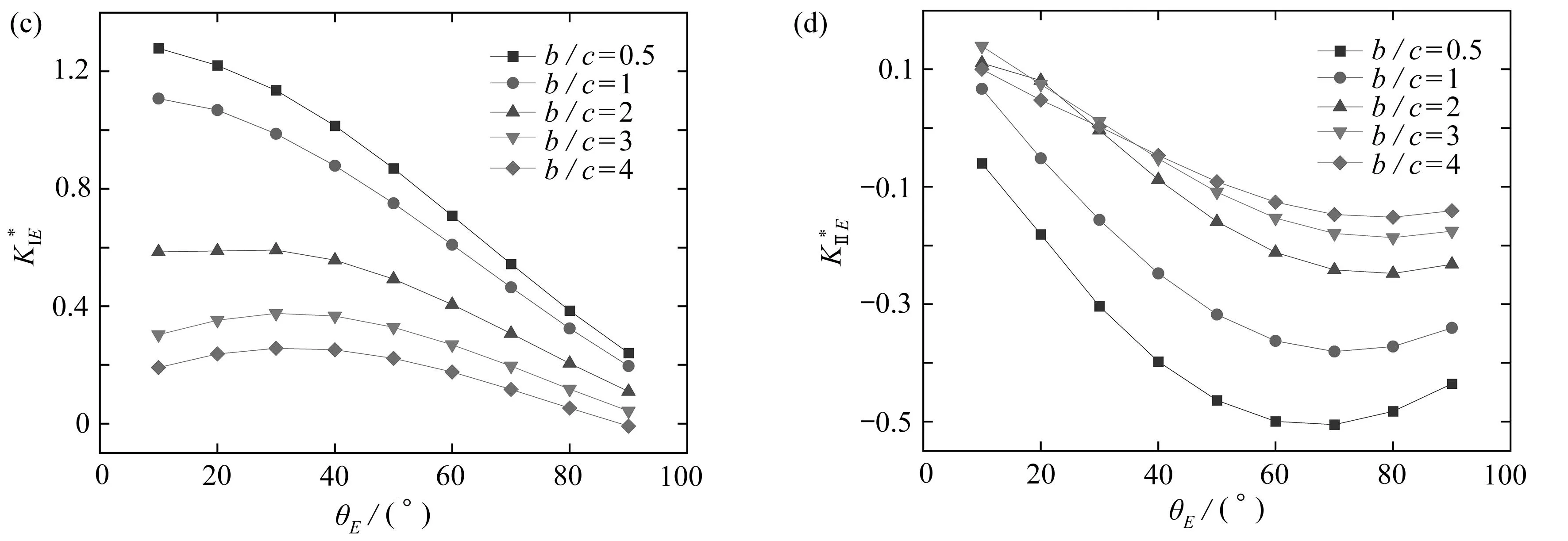
图7 分支长度比值对归一化应力强度因子的影响Fig. 7 Effects of branch length ratios on normalized stress intensity factors

4.5 分岔角度对和的影响

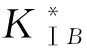
图8 分岔角度对归一化应力强度因子的影响Fig. 8 Effects of bifurcation angles on normalized stress intensity factors

4.6 多分支分岔裂纹的应力强度因子

本文所讨论的理论方法可以方便地应用到多分支的分岔裂纹问题(图9)中,相比较于以往解决的问题[15-17]更具工程价值,同时无需复杂的公式推导[18-19],只需要根据裂纹条数增加式(9)的个数,以及在分岔处根据式(11)进行相应的设置,便可以得到解答．令2a=4,2b=1,2c=0.5,θB=60°,θF=45°,将本文计算的结果与有限元进行比对,如表1所示．可见,本文给出的结果是可靠的,且相较于有限元计算而言,此方法可以方便快捷地用于解决多分支分岔裂纹问题,具有一定实际应用的价值．

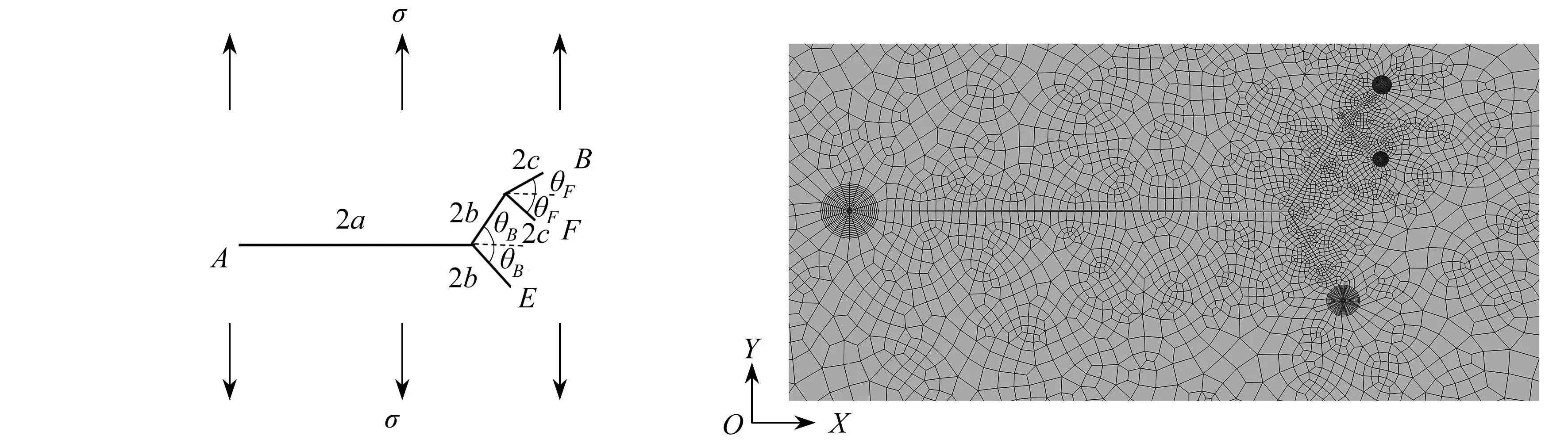
图9 多分支分岔裂纹示意图以及有限元网格划分局部图Fig. 9 Schematic diagram of the multiple branch bifurcation crack and the local partial finite element mesh

表1 多分支分岔裂纹有限元计算与本文结果对照

5 结 论

1) 由上述推导过程及计算结果可知,本文研究分岔裂纹的方法可靠且便捷,可用于更加复杂的多分支分岔裂纹问题(如鹿角型分岔裂纹)．

2) 随着埋入深度的增加,分岔裂纹两分支的应力强度因子均逐渐减小,且裂纹长度越长对于埋深变化越敏感．当埋深达到d/a=1.5时,分支裂尖应力强度因子最大的削弱程度可达15%左右,这说明随着埋深的增加,分岔裂纹向内部扩展会更加困难．

3) 分岔裂纹的分支长度越长,其应力强度因子越大,且长度较大的分支对长度较小的分支有一定的屏蔽作用,导致分岔裂纹更易向长分支方向扩展．在两分支裂纹长度比达到b/c=2以上时,屏蔽效应可达50%以上．

4) 随着荷载比值τ/σ的增加,当切应力大小与正应力大小相当时,分岔裂纹其中一分支的主导扩展模式由Ⅰ型扩展转变为Ⅱ型扩展,另一分支的Ⅰ型应力强度因子峰值角度会增大．