一种PID-PID串级控制系统的设计及其性能分析

刘悦婷, 孟维华, 丁建中

( 1.兰州文理学院 传媒工程学院, 兰州 730000; 2.甘肃省建筑设计研究院有限公司, 兰州 730030 )

0 引言

锅炉炉温控制系统是一个复杂的大滞后系统.近年来,随着对炉温控制系统的安全性和可靠性要求的不断提高,常规PID(proportional integral derivative)控制方法已无法达到预期的控制目标.为此,一些学者通过引入PID串级控制策略来提高了锅炉炉温控制系统的性能.例如:文献[1]的作者采用串级控制方式(其中主控制器采用模糊控制,副控制器采用PID控制)对锅炉炉温控制过程进行了研究,结果显示该方法可有效改善炉温系统的工作频率和输出温度.文献[2]的作者采用二自由度的GDC控制器对锅炉炉温的控制过程进行了研究,结果显示该方法可有效提高锅炉系统的响应速度和抗干扰能力.文献[3]的作者采用模糊内模PID控制方法对锅炉炉温的控制过程进行了研究,结果显示该方法可有效改善锅炉系统的动态特性和静态特性.文献[4]的作者采用增量式PID矫正控制方法对锅炉的控制过程进行了研究,结果显示该方法可有效提高锅炉系统的抗干扰能力和稳定性.文献[5]的作者将BP神经网络PID控制器应用于锅炉温控中,结果显示该方法可有效提高锅炉系统的动态性能和安全性.目前,对PID串级控制系统的参数进行定量计算和研究的较少[2];为此,本文针对工业用锅炉的物料出口温度具有大滞后的特点,设计了一种PID-PID串级控制系统,并通过定量计算和仿真实验验证了该控制系统的有效性.

1 PID-PID串级控制系统的设计及其性能分析

1.1 PID-PID串级控制系统的设计

本文设计的PID-PID串级控制系统的结构如图1所示.该控制器的主对象是管壁和原料;主被控量是原料的出口温度,用c1表示;副对象是炉膛;副被控量是炉膛温度,用c2表示;炉温控制系统的一次扰动包括原料的流量(负荷)、入口温度等,用q1表示;二次扰动包括燃油的阀前压力、燃油的热值和炉膛送风等,用q2表示.由于主被控量的给定值r1和主被控量的输出值c1是固定值,因此可将该串级控制系统的外环看作是一个恒值控制系统;由于该串级控制系统的内环副被控量的给定值r2和副被控量的输出值c2都是由主控制器实时控制的,因此可将内环看作是一个随动系统.

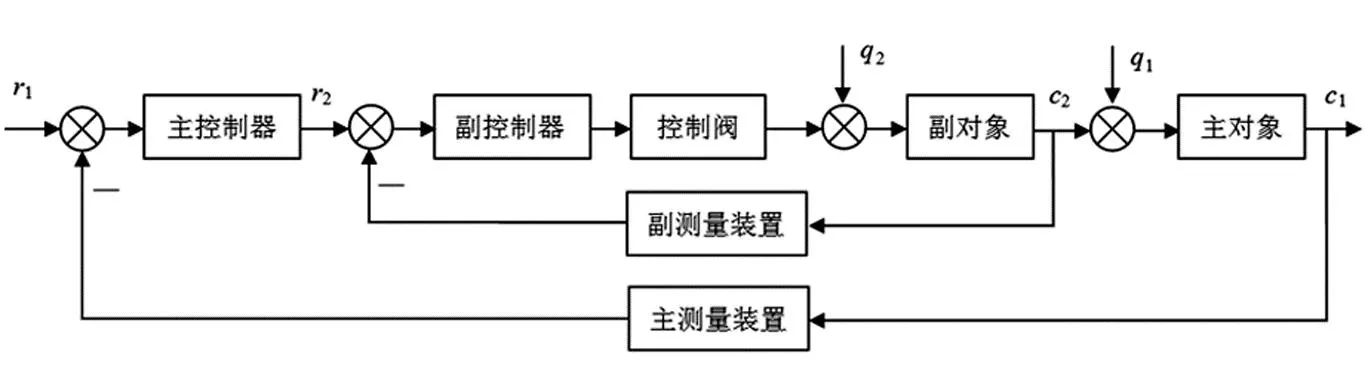
图1 PID-PID串级控制系统的结构

1.2 PID-PID串级控制系统的抗干扰性能分析

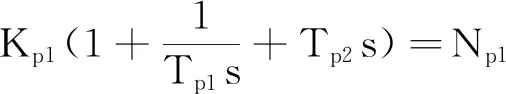
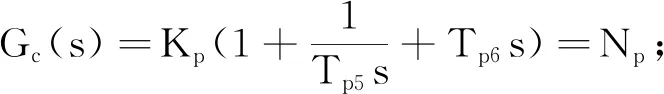
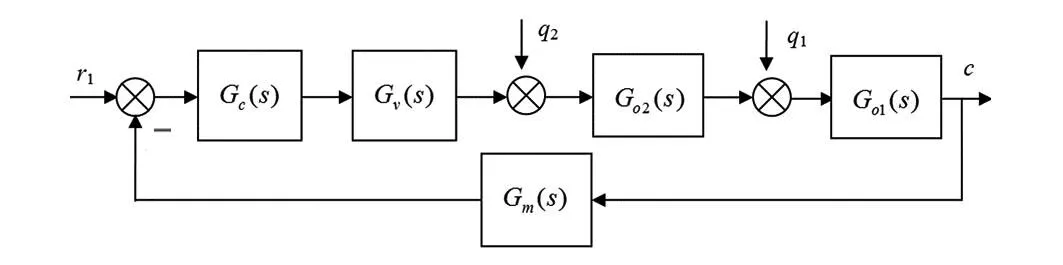
图2 单回路PID控制系统的结构

对单回路PID控制系统(图2所示)进行静态分析可得,c1对一次扰动q1和c1对二次扰动q2的闭环传递函数分别为:

(1)

(2)

将Gc(s)、Go1(s)、Go2(s)、Gm(s)和Gv(s)的传递函数分别代入式(1)和式(2)可得:

(3)

(4)

对PID-PID串级控制系统(图1所示)进行静态分析可得,c1对一次扰动q1和c1对二次扰动q2的闭环传递函数分别为:

(5)

(6)

将Gc1(s)、Gc2(s)、Go1(s)、Go2(s)、Gm1(s)、Gm2(s)和Gv(s)的传递函数表达式分别代入式(5)和(6)可得:

(7)

(8)

对比式(3)和式(7)的分母以及式(4)和式(8)的分母可知,PID-PID串级控制系统抗一次扰动和二次扰动的能力显著优于单回路PID控制系统.再对比式(8)和式(7)的值(式(8)的值小于式(7)的值)可知,PID-PID串级控制系统抗二次扰动的能力显著优于抗一次扰动的能力.

1.3 PID-PID串级控制系统的响应速度分析

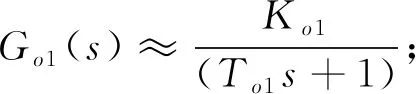
(9)

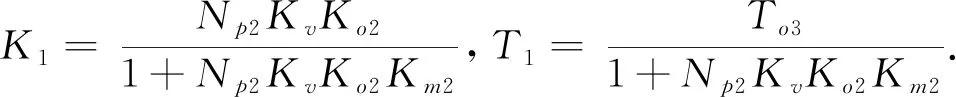
1.4 PID-PID串级控制系统的稳定性分析

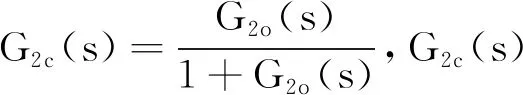
1.5 工作频率的分析

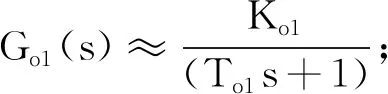
(10)

典型二阶系统的闭环传递函数[6]为:

(11)

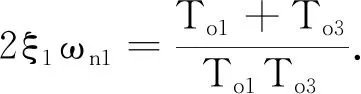
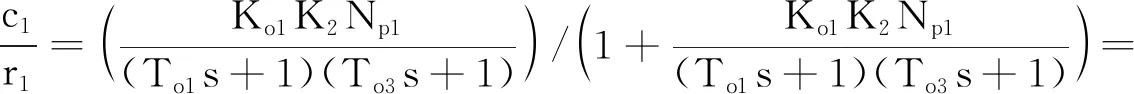
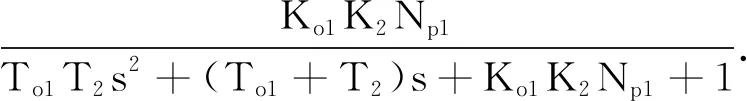
(12)

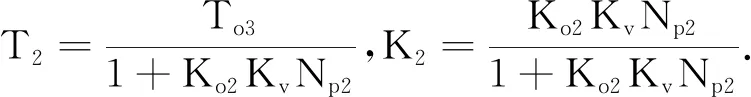
(13)

由于T2ω1.该结果说明PID-PID串级控制系统的工作频率高于单回路PID控制系统,且当PID-PID串级控制系统中的主、副对象的特性保持一定时,副控制器的增益越大系统的工作频率提高得越明显.

2 锅炉系统运行的温度数据采集和锅炉炉温控制系统的建模

2.1 温度数据采集

为了不干扰系统的正常运行,本文采用较大幅度的矩形脉冲作为输入信号以求得阶跃响应[7],如图3(a)所示.矩形脉冲信号由两个阶跃信号叠加而成[8],如图3(b)所示.当施加两个阶跃信号(在t=0处输入阶跃信号x1(t),在t=t0处输入与x1(t)大小相同、方向相反的信号x2(t)(x2(t)=-x1(t-t0))时,矩形脉冲信号可以表示为x(t)=x1(t)+x2(t).其中x1(t)和x2(t)的阶跃响应分别为y1(t)和y2(t).于是根据延迟定理可得,y2(t)=-y1(t-t0).再根据叠加原理可知,矩形脉冲响应y(t)可表示为y1(t)与y2(t)之和,即y(t)=y1(t)+y2(t)=y1(t)-y1(t-t0).对该式进行移项可得矩形脉冲的阶跃响应为y1(t)=y(t)+y1(t-t0).

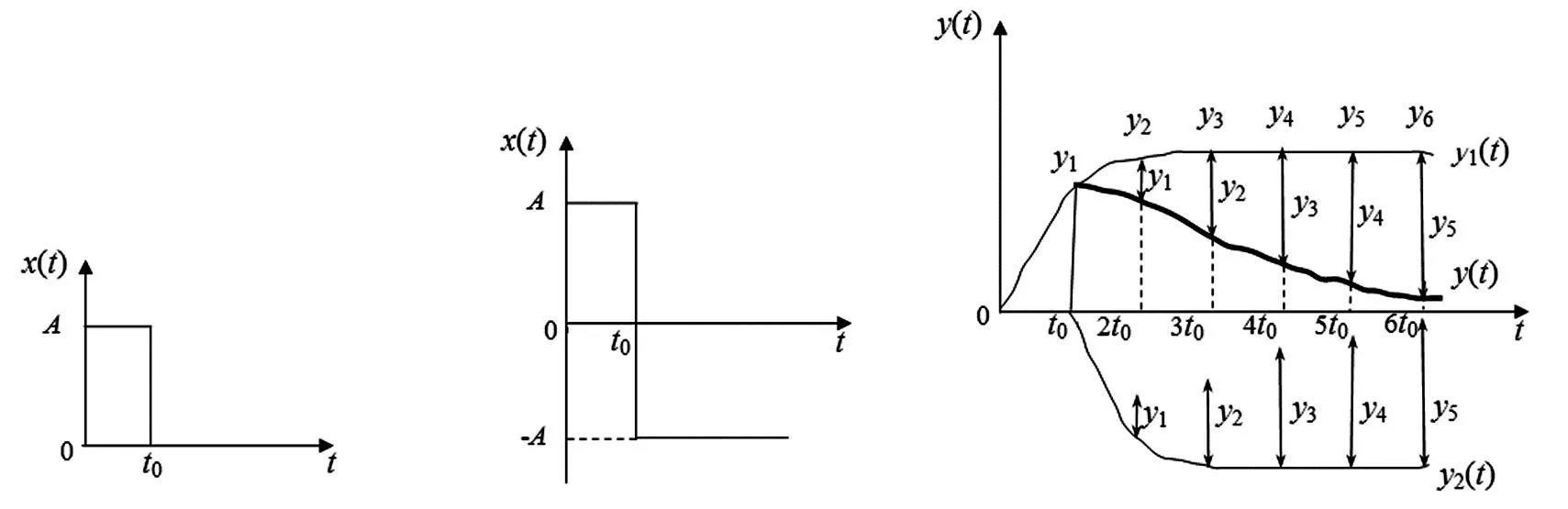
(a)单个阶跃信号的波形 (b)两个阶跃信号的叠加波形 (c)矩形脉冲的阶跃响应叠加过程

为求解阶跃响应y1(t),本文将响应曲线按时间间隔t0进行了等分.第1区间为t≤t0,即y1(t)=y(t),y1(t0)=y(t0);第2区间为y1(t)=y(t)+y1(t-t0),即y1(2t0)=y(2t0)+y1(t0);第3区间为y1(3t0)=y(3t0)+y1(2t0).按上述类推,即可得上述计算区间的阶跃响应曲线(由上述区间的脉冲响应曲线与前一区间的阶跃响应曲线叠加而成),如图3(c)所示.

2.2 锅炉炉温控制系统的建模

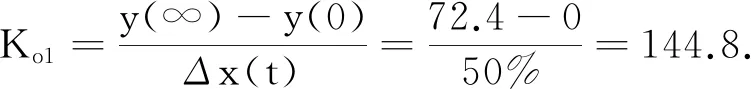
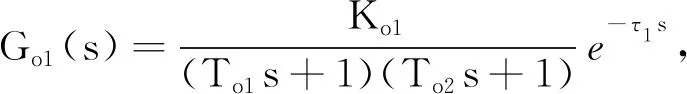
(14)

同理,可得锅炉炉温控制系统副对象的传递函数为:

(15)

3 实验结果与分析

某锅炉系统如图4所示.系统中主被控量是原料的出口温度,副被控量是炉膛温度.应用PID-PID串级控制系统时,主、副对象的传递函数分别采用如式(14)和式(15)所示的函数,主、副控制器的传递函数分别为:

(16)

图4 锅炉系统现场运行图

(17)

实验以CX-Programmer、Windows为平台.单回路控制系统的Simulink模型如图5所示.本文采用Ziegler-Nichols方法[12]整定单回路控制系统的PID参数.经整定,得单回路PID控制器的比例系数、积分系数、微分系数分别为0.000044、0.0000002、0.003.由所得参数得到的系统的阶跃响应输出如图6所示,系统在一次扰动作用下的误差输出如图7所示,系统在二次扰动作用下的误差输出如图8所示.

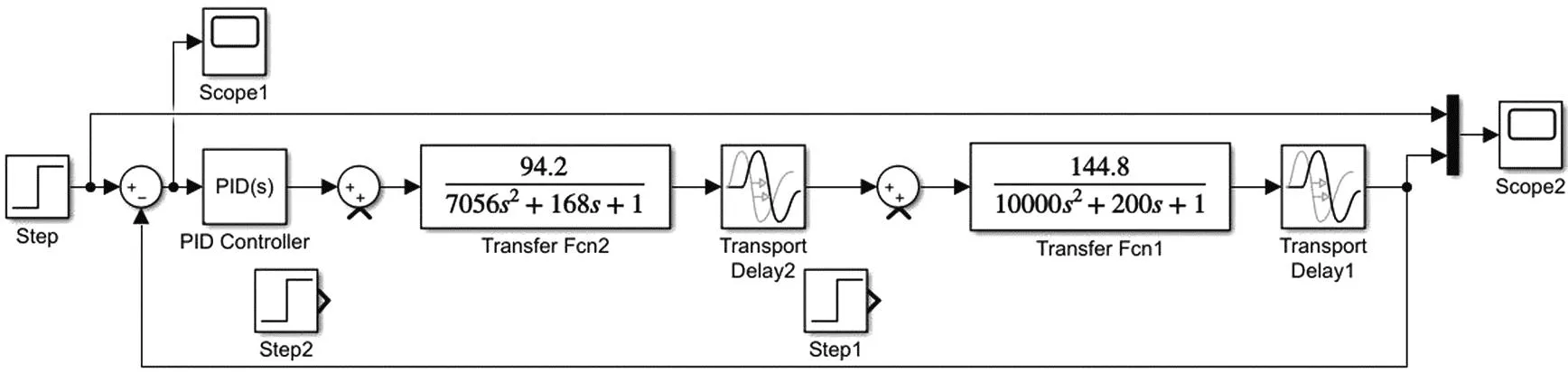
图5 单回路PID控制系统的Simulink模型

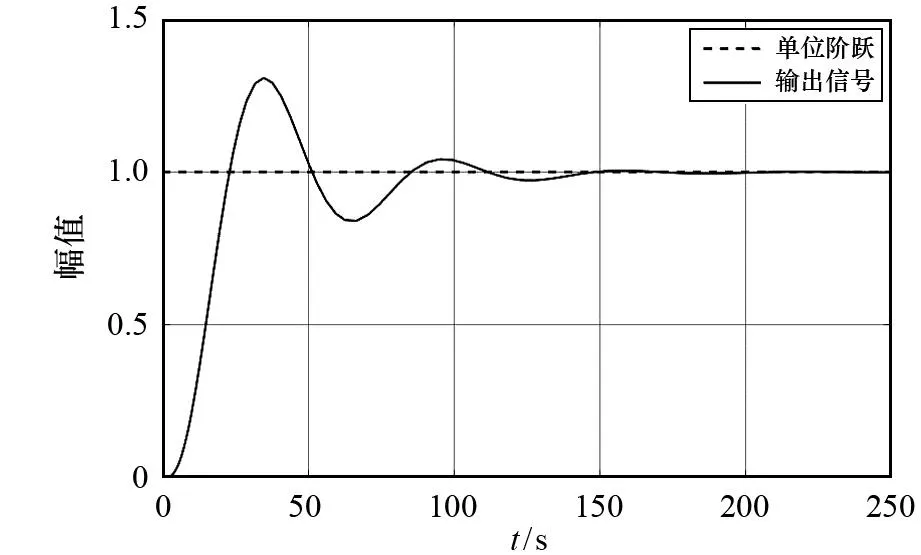
图6 单回路PID控制系统的阶跃响应输出

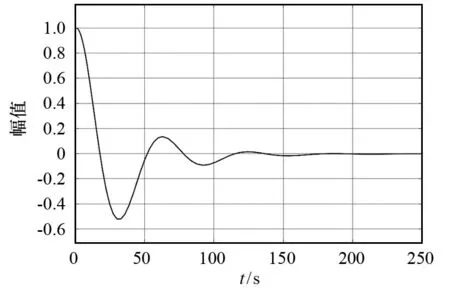
图7 单回路PID控制系统在一次扰动作用下的误差输出

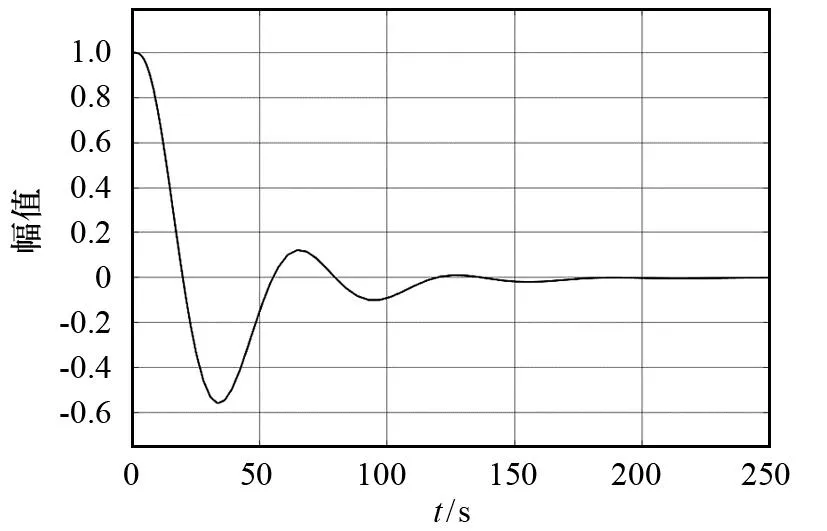
图8 单回路PID控制系统在二次扰动作用下的误差输出

PID-PID串级控制系统的Simulink模型如图9所示.本文采用一步法整定PID-PID串级控制器的PID参数.经整定,得主PID控制器的比例系数、积分系数、微分系数分别为0.0065、0.00004、0.22,副PID控制器的比例系数、积分系数、微分系数分别为0.05、0.0007、2.5.由所得参数得到的PID-PID串级控制系统的阶跃响应输出如图10所示,系统在一次扰动作用下的误差输出如图11所示,系统在二次扰动作用下的误差输出如图12所示.

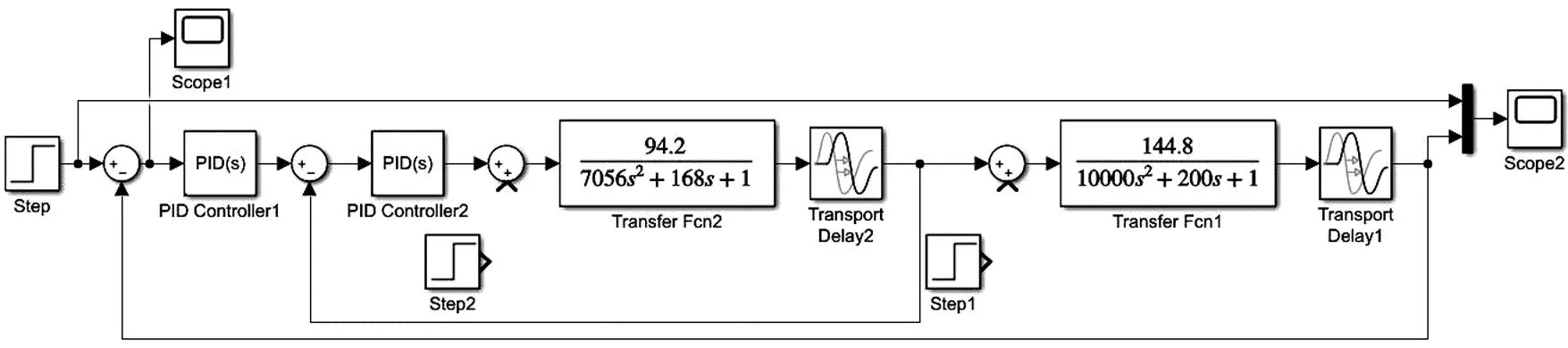
图9 PID-PID串级控制系统的Simulink模型

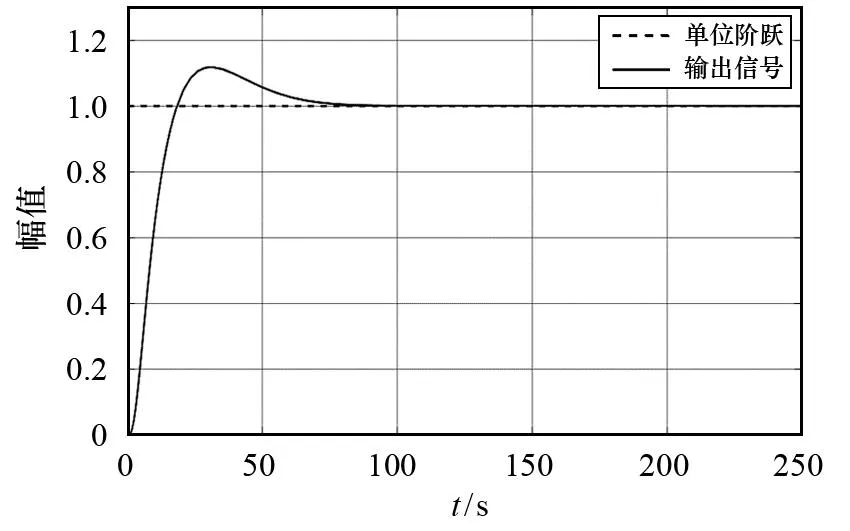
图10 PID-PID串级控制系统的阶跃响应输出

图11 PID-PID串级控制系统在一次扰动作用下的误差输出

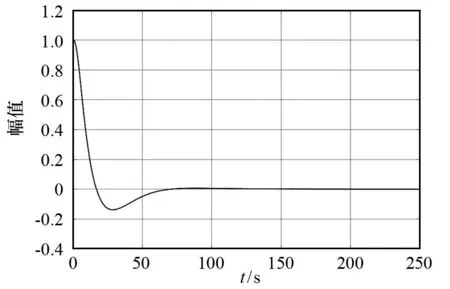
图12 PID-PID串级控制系统在二次扰动作用下的误差输出

单回路PID控制系统和PID-PID串级控制系统的衰减率、调节时间、残偏差、二次阶跃扰动下的系统短期最大偏差、一次阶跃扰动下的系统短期最大偏差如表1所示.

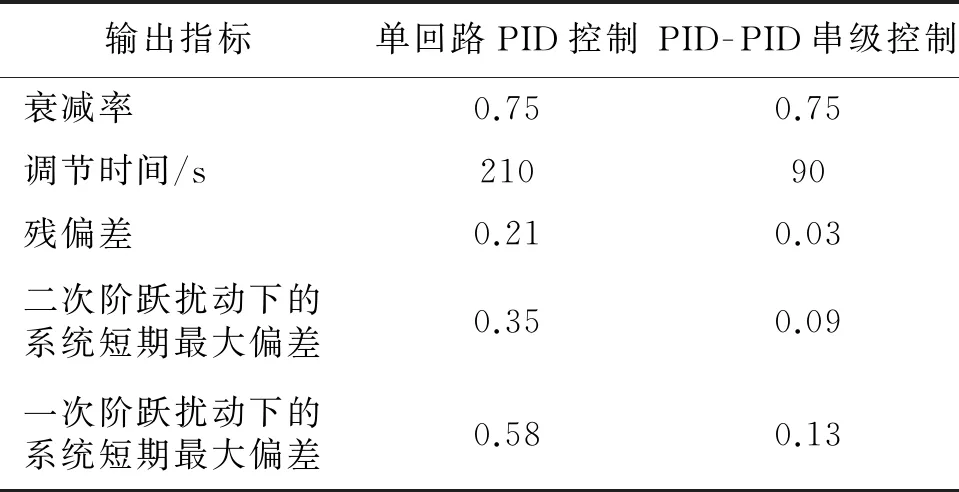
表1 单回路PID控制和PID-PID串级控制时系统的输出指标

对比图6和图10可知,PID-PID串级控制响应速度(调节时间为90 s,超调量为9%)显著优于单回路PID控制响应速度(调节时间为210 s,超调量为38%),由此表明PID-PID串级控制系统的动态性能显著优于单回路PID控制系统.

对比图7和图11可知,PID-PID串级控制系统在一次扰动作用下其误差输出达到0的时间(70 s)显著低于单回路PID控制系统(170 s),且达到0之前无振荡,而单回路PID控制系统则出现多次振荡.对比图6和图10可知,PID-PID串级控制系统在二次扰动作用下其误差输出达到0的时间(60 s)显著低于单回路PID控制系统(170 s),且达到0之前无振荡,而单回路PID控制系统则出现多次振荡.这表明,PID-PID串级控制系统具有更好的抗干扰性和稳定性.

由表1中的数据也可以看出,PID-PID串级控制系统的动态性能显著优于单回路PID控制系统,且其系统的抗二次扰动能力也显著优于其抗一次扰动能力.该结果进一步说明,PID-PID串级控制系统的性能显著优于单回路PID控制系统.

4 结论

实验表明,本文提出的PID-PID串级控制系统的抗干扰性能、响应速度、稳定性和工作频率比单回路PID控制系统分别提高了24%、32%、37%、41%,同时PID-PID串级控制系统的抗二次扰动能力也显著优于其抗一次扰动能力.此外,本文提出的控制方法还具有简单和易于实现的优点,因此本文的研究结果可为锅炉炉温控制系统的设计提供参考.在今后的研究中,我们将探讨智能优化算法在PID参数整定中的应用,以此进一步提高锅炉炉温的控制效果.