精密仪器承载板的多尺度轻量化设计

张永弟,眭君娜,王伟志,杨 光

(1.河北科技大学机械工程学院,河北石家庄 050018;2.河北省通用航空增材制造协同创新中心,河北石家庄 050018)

精密仪器承载板作为一种辅助承载结构,对设备具有辅助定位、保护等功能,在飞行器的舱体等处得到广泛应用。在满足强度要求、安装要求的前提下,仪器承载板尽可能质量最轻、刚度最好。传统的轻量化设计方法有轻质材料的应用、制造工艺优化和简单的结构优化[1]。增材制造结合有限元分析,促使出现了宏观层面的拓扑优化、微观层面的点阵优化以及结合宏微观2种尺度的优化设计等多种轻量化设计方法[2-4]。

拓扑优化是根据给定的载荷工况、性能指标和约束条件对材料进行合理分配、确定最优传力路径的结构优化设计方法[5]。王瑞显等[6]对钛合金卫星星敏支架进行拓扑优化设计,采用形貌优化对支架进行光顺处理,利用选区激光熔融成形工艺制造的星敏支架减重达80%。法国的空客公司对A350 XWB用金属打印的钛合金客舱支架连接器代替原来的铝合金铣削制造的支架,重量减轻30%以上,废料由95%降低至5%[7]。飞机制造巨头通用电气公司结合增材制造和拓扑优化技术生产的LEAP(light enabled additive production)钴合金发动机燃料喷嘴在降低重量的同时延长了使用寿命[8]。瑞士的RUAG公司采用拓扑优化技术生产的哨兵卫星天线支架由1.6 kg减轻到940 g,并将刚度提升了30%[9]。点阵结构因具有高比刚度、隔热、减震以及吸能等特性被广泛应用于轻量化设计[10-11]。点阵优化通俗来讲就是将点阵结构填充到待优化区域,在轻量化的同时维持或增强模型的特定力学性能[12]。张牧尧等[13]基于移动阈值切面法设计的非均匀点阵结构填充到小口径的金属反光镜上,质量减轻了20%的同时还有效抵消了部分安装应力。张龙等[14]为满足航天器载荷支撑的轻量化要求,提出一种封闭蒙皮包裹三维点阵层级结构的设备支撑结构形式并设计出相应模型,运用选区激光熔融技术制造出的实物减重46.4%,并通过了振动力学实验验证。俄罗斯的赫鲁尼切夫生产的航天重型发射器运用点阵结构,使得火箭的质量显著减少且有效载荷得到相应增加[15]。欧洲航天局联合澳大利亚的蒙纳士大学将点阵结构应用于小推力火箭发动机的外壁并成功发射[16]。

多尺度轻量化设计即结合拓扑优化和点阵优化2种技术,使得机械结构在宏观和微观层面上达到减重的目的。LIU等[17]利用拓扑优化和点阵优化技术,设计了一种高刚度重量比的轻质夹层飞机扰流板,重量减轻了80%。DUAN等[18]对纤维复合材料结构进行了拓扑优化和纤维铺设角度优化,体积分数降低了92.78%,刚度特性更加均匀。WANG等[19]针对承受轴向载荷的耐撞结构,利用多尺度协同设计方法以一体化的方式优化宏观材料密度分布和微观单元拓扑,获得结构的最佳刚度。谷小军等[20]对民用飞行器的摇臂结构和铰链臂结构在拓扑优化的基础上进行点阵结构填充,重量分别减轻了10%和30%。由此可知,采用多尺度轻量化设计方法比单独采用一种方法在减重和性能提升方面综合效果更好。因此,本文从拓扑优化和点阵优化2种尺度对精密仪器承载板进行减重和刚度提升的优化设计,以更好地满足实际工况需求。

1 边界条件和设计流程

仪器承载板与仪器舱体采用螺栓连接的形式,精密仪器通过螺钉安装在仪器承载板上。工作设备总长465 mm,宽242 mm,高200 mm,安装时距板后端10 mm,安装孔的长度方向间距200 mm,宽度方向间距204 mm,整个设备重20 kg。舱体情况如图1所示。采用Solidworks软件对仪器承载板和舱体进行建模,如图2所示,仪器承载板的模型重量为14.723 kg。

图1 舱体情况

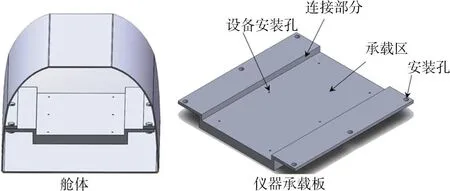
图2 舱体和仪器承载板

仪器承载板采用铝合金制造,材料的相关性能如表1所示。仪器承载板除了承受来自设备的重量之外,还要受到来自仪器舱体通过安装孔传递而来的载荷和高速机动下的大惯性载荷。舱体在工作时的气动载荷转换为舱体前端的等效工作载荷,具体等效工作载荷如表2所示。此外,考虑仪器整个结构在高速机动下产生的沿舱体轴向的-32倍的重力加速度和沿法向的20倍重力加速度的惯性载荷。对舱体的尾端施加固定约束。

表1 仪器承载板的材料性能

表2 舱体前端等效工作载荷

轻量化流程首先是利用ANSYS有限元软件获得模型的力学性能和固有频率,确定优化区域,并进行拓扑优化,检验重构模型的优化区域是否得到改善。定义需要点阵优化的区域,利用SolidThinking Inspire软件对点阵结构进行格栅填充比、格栅结构和体积约束的三水平三因素正交实验,直至结果符合要求。

2 仪器承载板的多尺度优化

2.1 仪器承载板拓扑优化

采用ANSYS软件对仪器承载板进行拓扑优化前的力学分析和模态分析。对仪器承载板进行网格划分后等一系列前处理后,进行有限元分析得到的力学性能如图3所示,可以看出仪器承载板在过载状态(即在加速度状态下)下的米塞斯应力为104.71 MPa,最大变形为2.099 5 mm。模态分析数据如表3所示。模态分析获得的频率是评价结构动力学性能的重要指标[21]。对于本仪器承载板来说,其结构的模态频率越高越好。

表3 仪器承载板模态分析结果

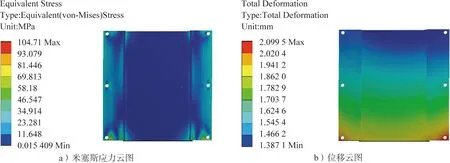
图3 过载下仪器承载板的力学分析云图

除与设备和舱体进行连接的孔外,其他部分全部被定义为优化区域,以最小柔顺度为约束条件、质量最小为优化目标对仪器承载板进行过载下的拓扑优化。经过多次迭代,得到的仪器承载板的概念云图如图4 a)所示。图4 a)中材料密度在0～0.4之间的红色部分表示材料去除区域(因材料去除故未显示);密度在0.4～0.6之间的橘色部分为材料过渡区域,保留与否可经过模型重构后的力学分析决定;密度在0.6～1.0之间的灰色部分为保留区域。

图4 仪器承载板拓扑重构图

根据优化结果对仪器承载板进行模型重构,应注意选区激光熔融的设计规则和约束问题;该结构安装在舱体上,所以要考虑与舱体的装配问题;根据模型的概念云图可以看出承载区结构厚度偏厚,应当进行适当的去除。所以改进优化方案如下。

1)改善部分结构

由于原结构的连接部分是直角过渡结构,结构的突变容易造成应力集中,增加断裂的风险,所以改善为更平滑的斜面过渡结构,降低零件应力集中的影响,延长零件的使用寿命。

2)改变结构厚度

根据模型的概念云图,将承载区的底板厚度由原来的30 mm变薄为15 mm。

重构后的仪器承载板如图4 b)所示。

进行过载下的力学分析和模态分析,优化后的力学性能分析如图5所示,拓扑后的模态分析的前6阶固有频率如表4所示。

表4 拓扑重构仪器承载板模态分析结果

图5 重构后仪器承载板力学分析云图

根据图5可以看出,拓扑重构后的仪器承载板过载下的最大米塞斯应力为142.91 MPa,最大变形为2.474 mm。与拓扑前的结构比较而言,重构后的仪器承载板质量减轻9.355 kg,米塞斯应力仅增加38.2 MPa,位移增加0.374 5 mm,其刚度和强度略有下降,经式(1)计算可知安全系数n=3.53,所以优化后的仪器承载板其安全性能符合要求。与重构前的结构的模态频率(见表3)对比,拓扑后的仪器承载板除1阶模态外,其他5阶模态频率都大于未拓扑优化前,说明拓扑后的结构其动力学性能得到提升。

(1)

式中:n为安全系数;σs为材料的屈服强度;σmax为仪器承载板的最大应力。

2.2 重构后仪器承载板的点阵优化

通过拓扑优化的结果分析,重构后的仪器承载板重量大幅度减轻,刚度和强度略微下降,其力学云图和安全系数说明重构后的仪器承载板还有轻量化的空间,故依靠点阵结构的优良性能对仪器承载板进行点阵优化的同时提升其刚度。

采用SolidThinking Inspire软件作为点阵优化的工具,对拓扑优化重构后的仪器承载板进行点阵优化。为了保护连接的部分,以螺栓孔为中心半径增加1.5 mm,螺钉孔为中心半径增加1 mm,对仪器承载板进行分隔,分割结果如图6所示。图6中深色部分为优化区域,浅色部分为未优化区域;同样以最小柔顺度为约束,以质量最小为目标对仪器承载板进行点阵优化。

图6 点阵优化前处理

对点阵结构的合理选用可以实现目标模型的最佳轻量化,同时提高模型的特定力学性能。格栅结构作为典型的轻质化结构,因具有承载能力强、结构稳定性好以及结构效率高等特点,被广泛应用于航天主承力结构中[22-23]。

为进一步提高分析的准确性,以格栅结构、格栅填充比和体积约束作为点阵优化的可变参数,利用仿真进行三水平三因素正交试验。格栅结构作为点阵结构的一种类型,包括目标长度、最小直径和最大直径。格栅填充比即在填充过程中格栅结构占整个模型的百分比。体积约束指在优化过程中,质量占整个设计空间的百分比。格栅结构如表5所示,正交因素试验安排如表6所示,整个正交试验如表7所示。

表5 格栅结构

表6 正交因素试验设置

表7 正交试验

2.3 正交试验结果分析

根据点阵优化正交试验,所得结果如表8所示。根据点阵正交结果实验表,绘制如图7所示的三因素三水平正交试验结果图并得到表9所示的三因素极差分析表。

表8 点阵优化正交试验结果

表9 三因素极差分析表

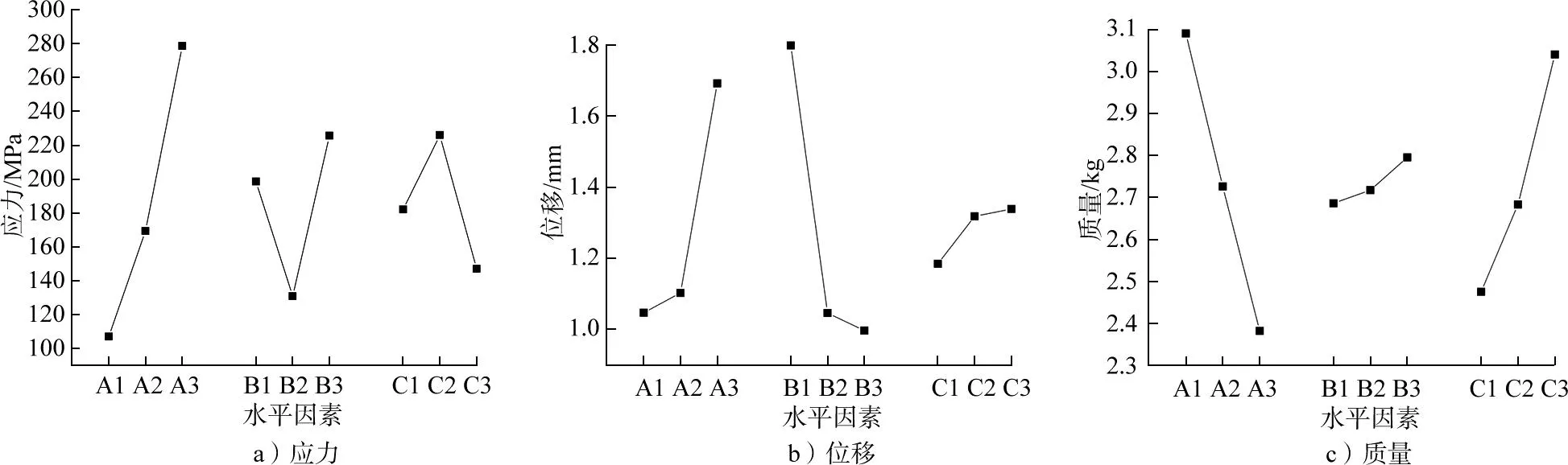
图7 点阵优化正交试验结果

依据点阵优化正交试验结果表,可以看出,无论从应力、位移还是质量方面,都符合优化要求。结合表9三因素极差分析表,由图7 a)可知,因素A对应力的影响最大;因素A对应力的影响为上升趋势,因素B对应力的影响为先下降后上升的V字型趋势,因素C为先上升后下降的V字型趋势,应力最小的因素组合为A1B2B3。由图7 b)可知,因素B对位移的影响最大;因素A对位移的影响为上升趋势,因素B对位移的影响为下降趋势,因素C对位移的影响为上升趋势,位移最小的因素组合为A1B3C1。由图7 c)可知,因素A对质量的影响最大;因素A对质量的影响为下降趋势,因素B对质量的影响为上升趋势,因素C对质量的影响也为上升趋势,质量最小的因素组合为A3B1C1。

由于优化的主要目的是为了减重,所以在保证应力和位移满足要求的前提下,追求更轻的质量,故选择A3B1C1三因素作为最终的点阵优化因素。优化的力学分析结果如图8所示。从图8可以看出,优化后的米塞斯应力为281.20 MPa,位移为1.489 mm。模态分析如表10所示,可以看出,仪器承载板的前6阶频率均高于拓扑优化后的前6阶频率。

表10 拓扑重构仪器承载板模态分析结果

图8 点阵优化过载下力学分析结果

2.4 精密仪器承载板优化前后对比

图9为精密仪器承载板原模型、拓扑优化以及拓扑点阵优化后的力学性能对比结果,从图9可以看出,经过多尺度优化后的精密仪器承载板质量减轻12.703 kg,减轻了85.2%;应力由原先的104.71 MPa增加到281.20 MPa,根据式(1)计算可知安全系数n为1.796,符合航天器结构的设计安全系数1.25的要求;位移由原先的2.10 mm降为1.49 mm,变形量降低29.07%,说明精密仪器承载板的刚度得到提升。

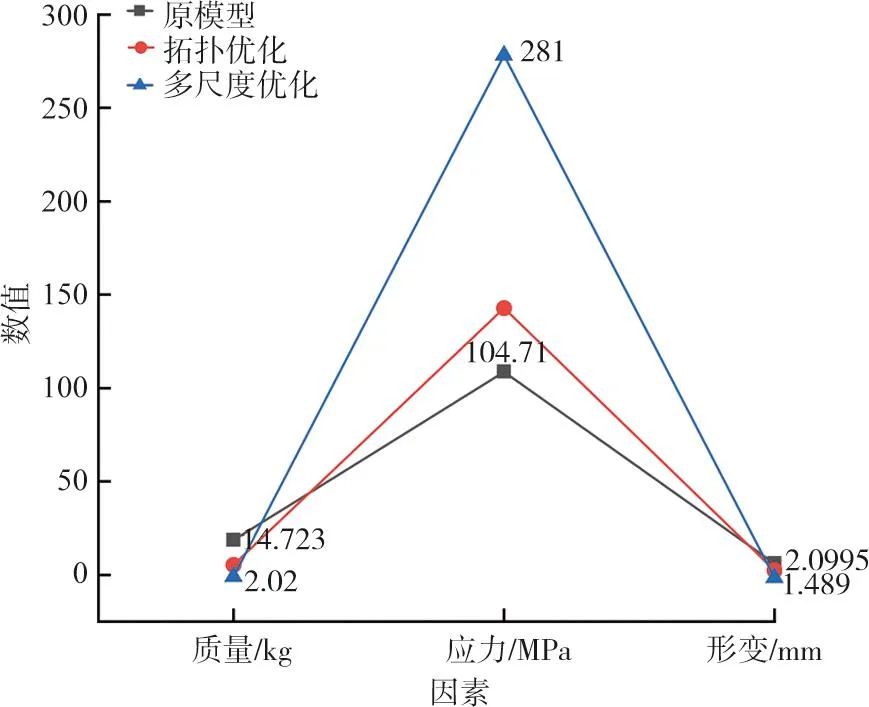
图9 多尺度优化前后力学性能对比

图10为精密仪器承载板原模型、拓扑优化以及多尺度优化后的模态频率数据,从图10可以看出,精密仪器承载板的模态频率由原先的79.91 Hz增加到99.97 Hz,提升了22.6%,说明结构的动力学性能得到提升,其稳定性得到进一步增强。

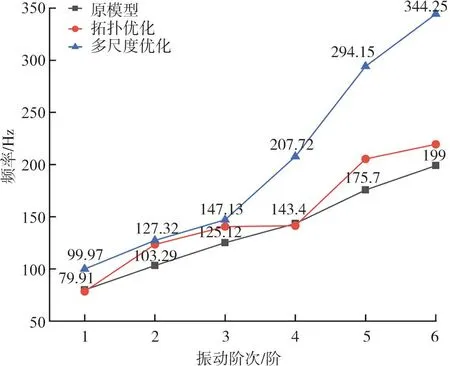
图10 多尺度优化前后固有频率对比

3 结 语

本文提出了一种宏观结构拓扑和微观结构点阵优化相结合的多尺度轻量化设计方法,实现了过载工况下仪器承载板的结构刚度最大化和质量最小化。其相关的数值分析表明:1)仪器承载板的最大变形量降低了29.07%,说明其结构的刚度得到大幅度增强;2)拓扑优化和多尺度优化后模型的固有频率均高于原模型,说明仪器承载板的动力学性能得到显著提升,并具备一定的减震功能。研究结果为航空航天结构的轻量化设计提供了参考。

本文只针对精密仪器承载板单个零件进行了多尺度优化研究,后续可对具有配合关系的零件进行设计分析,发挥增材制造先进制造技术的优势,将不同零件、不同功能整合到一个零件上,并进行多尺度优化设计。

参考文献/References：

[1] 魏晓荣.工程机械轻量化方法与设计探究[J].机械工业标准化与质量,2022(9):32-35.

WEI Xiaorong.Research on lightweight method and design of construction machinery[J].Machinery Industry Standardization &Quality,2022(9):32-35.

[2] 余海伟,袁军堂,汪振华.面向增材制造的轻量化炮口制退器创新构型设计与性能改进[J].机械设计,2021,38(sup2):40-45.

YU Haiwei,YUAN Juntang,WANG Zhenhua.Novel design of lightweight muzzle brake with enhanced performance for additive manufacturing[J].Journal of Machine Design,2021,38(sup2):40-45.

[3] 王伟,袁雷,王晓巍.飞机增材制造制件的宏观结构轻量化分析[J].飞机设计,2015,35(3):24-28.

WANG Wei,YUAN Lei,WANG Xiaowei.Macro-structural lightweight analysis for aircraft parts made by additive manufacturing techno-logy[J].Aircraft Design,2015,35(3):24-28.

[4] 许琦,阎军,蒋存存,等.航天器点阵夹层圆柱壳构型多学科优化设计[J].载人航天,2020,26(2):152-158.

XU Qi,YAN Jun,JIANG Cuncun,et al.Multi-disciplinary optimization design of multi-layer lattice sandwich cylindrical shell in spacecraft[J].Manned Spaceflight,2020,26(2):152-158.

[5] 孟亮,仲明哲,李文彪,等.面向增材制造的航空发动机外部系统支架拓扑优化设计[J].中国机械工程,2022,33(23):2822-2832.

MENG Liang,ZHONG Mingzhe,LI Wenbiao,et al.Topology optimization design of aero-engine external system brackets for additive manufacturing[J].China Mechanical Engineering,2022,33(23):2822-2832.

[6] 王瑞显,冯振伟,马灵犀,等.小卫星一体化星敏支架拓扑优化[J].南京航空航天大学学报,2021,53(sup1):67-70.

WANG Ruixian,FENG Zhenwei,MA Lingxi,et al.Topology optimization of sensor brackets for small satellites[J].Journal of Nanjing University of Aeronauticsand Astronautics,2021,53(sup1):67-70.

[7] KUMAR L J,KRISHNADAS NAIR C G.Current Trends of Additive Manufacturing in the Aerospace Industry[C]//Advances in 3D Printing &Additive Manufacturing Technologies.Singapore:Springer,2017:39-54.

[8] BLAKEY-MILNER B,GRADL P,SNEDDEN G,et al.Metal additive manufacturing in aerospace:A review[J].Materials &Design,2021,209.DOI:10.1016/j.matdes.2021.110008.

[9] MOURIAUX F,BERKAU A.Certified foruniversal success:Additive manufacturing of satellite components[Z].Krailling/Munich:EOS,2018.

[10] 方泽辉,李鑫宇,蒋钰婷,等.基于拓扑优化的泡沫填充点阵结构力学行为研究[J].机械制造,2021,59(10):1-5.

FANG Zehui,LI Xinyu,JIANG Yuting,et al.Research on mechanical behavior of foam filled lattice structure based on topology optimization[J].Machinery,2021,59(10):1-5.

[11] 董伟,李扬,辛克浩,等.基于拓扑优化的点阵-加筋板式结构设计方法[J].西北工业大学学报,2021,39(6):1233-1239.

DONG Wei,LI Yang,XIN Kehao,et al.A method of designing plate structure consisting of lattices and stiffeners based on topology optimization[J].Journal of Northwestern Polytechnical University,2021,39(6):1233-1239.

[12] 朱健峰,戴宁,刘乐乐.功能性点阵结构设计优化技术研究[J].机械设计与制造工程,2020,49(7):1-6.

ZHU Jianfeng,DAI Ning,LIU Lele.Research on the design and optimization technology of functional lattice structure[J].Machine Design and Manufacturing Engineering,2020,49(7):1-6.

[13] 张牧尧,苏云,王超.基于空间反射镜的点阵结构非均匀尺寸优化设计[J].航天返回与遥感,2021,42(2):123-129.

ZHANG Muyao,SU Yun,WANG Chao.Anon-uniform lattice structure size optimization design based on space mirror[J].Spacecraft Recovery &Remote Sensing,2021,42(2):123-129.

[14] 张龙,李昂,赵云鹏,等.一种全封闭蒙皮点阵支撑结构的优化设计与试验验证[J].机械工程学报,2021,57(22):35-42.

ZHANG Long,LI Ang,ZHAO Yunpeng,et al.Optimal design and experimental verification of an enclosed skin lattice support structure[J].Journal of Mechanical Engineering,2021,57(22):35-42.

[15] VASILIEV V V,BARYNIN V A,RAZIN A F.Anisogrid composite lattice structures:Development and aerospace applications[J].Composite Structures,2012,94(3):1117-1127.

[16] 吉芬,廖宝华,柏林,等.激光选区熔化成形点阵结构应用研究[J].航空科学技术,2022,33(9):17-25.

JI Fen,LIAO Baohua,BAI Lin,et al.The SLM technology application research on lattice structure[J].Aeronautical Science and Technology,2022,33(9):17-25.

[17] LIU Jie,OU Haifeng,HE Junfeng,et al.Topological design of a lightweight sandwich aircraft spoiler[J].Materials,2019,12(19).DOI:10.3390/ma12193225.

[18] DUAN Zunyi,LIU Yuqi,FAN Junling,et al.Concurrent multi-material and multi-scale design optimization of fiber-reinforced composite material and structures for minimum structural compliance[J].Composite Structures,2023,311.DOI:10.1016/j.compstruct.2023.116796.

[19] WANG Xi,QIN Ruixian,CHEN Bingzhi,et al.Multi-scale collaborative optimization of lattice structures using laser additive manufacturing[J].International Journal of Mechanical Sciences,2022,222.DOI:10.1016/j.ijmecsci.2022.107257.

[20] 谷小军,李城彬,王文龙,等.拓扑优化与增材制造技术的融合及其在民用飞行器设计中的应用[J].航空制造技术,2022,65(14):14-20.

GU Xiaojun,LI Chengbin,WANG Wenlong,et al.Integration of topology optimization and additive manufacturing technology and its application in civil aircraft structural design[J].Aeronautical Manufacturing Technology,2022,65(14):14-20.

[21] 李龙飞,李树彦,侯得锋,等.半导体设备承载板的模态分析及拓扑优化[J].电子工业专用设备,2022,51(5):56-59.

LI Longfei,LI Shuyan,HOU Defeng,et al.Modal analysis and topology optimization of the bearing plate for semiconductor equipment[J].Equipment for Electronic Products Manufacturing,2022,51(5):56-59.

[22] 蒋诗才,石峰晖.碳纤维复合材料格栅结构的吸波/承载性能研究[J].舰船电子工程,2019,39(3):82-86.

JIANG Shicai,SHI Fenghui.Study on microwave-absorbing and mechanical properties of advanced stiffened grid structure for carbon fiber[J].Ship Electronic Engineering,2019,39(3):82-86.

[23] 于雅琳,李健芳,黄智彬,等.复合材料负泊松比格栅结构设计及力学性能评价[J].复合材料学报,2021,38(4):1107-1114.

YU Yalin,LI Jianfang,HUANG Zhibin,et al.Structural design and mechanical characterization of an auxetic advanced grid structure composite[J].Acta Materiae Compositae Sinica,2021,38(4):1107-1114.