基于MVMD-MOMEDA的齿轮箱故障诊断方法

崔素晓,崔彦平,武 哲,吕志元,张琳琳

(河北科技大学机械工程学院,河北石家庄 050018)

齿轮箱作为传统机械部件,运行稳定、传动效率高,被广泛应用于风力发电机组中[1]。研究表明,齿轮及轴承故障频率多发,是影响齿轮箱正常工作运转的关键原因[2]。由于齿轮箱结构复杂,发生故障时,所提取到的信号特征是多种故障共同混叠、耦合的结果,再加上早期微弱故障信号受复杂传递路径和强背景噪音的影响,增加了故障特征提取识别的难度[3-4]。因此,找到一种最优滤波器对齿轮箱进行故障诊断,实现早期故障的精准定位,对降低重大事故发生概率具有重要意义。

许多学者在有效识别故障信号并对其分类方面做了大量研究[5-9],目前已有多种算法来处理旋转机械非平稳、非线性的故障冲击信号。针对非平稳信号,经验模态分解(empirical mode decomposition,EMD)可以实现非平稳信号分量与噪音分量自动分离,选择需要的分量重构,进而实现去噪的目的,但存在过分解、欠分解、端效应、模态混叠等缺陷[10-12];DRAGOMIRETSKIY[13]提出了变分模态分解(variational mode decomposition,VMD)来克服EMD算法的不足。VMD是一种完全非递归的分解方法,对噪声具有鲁棒性,但需要预先定义模态数K,且不能将原始信号中的直流分量进行很好的分离[14-16];在VMD基础上扩展出了多元变分模态分解(multielementvariational mode decomposition,MVMD)[17],该方法通过构建变分优化问题,提取多元信号固有的多元调制振荡,用于处理包含任意数量通道的多元数据,有效抑制端点效应,避免模态混叠,但仍存在初始参数选择问题。反卷积方法是另一种广泛的信号处理方法,MCDONALD[18]提出了多点最优最小熵反褶积调整(multipoint optimal minimum entropy deconvolution with convolution adjustment,MOMEDA),该算法主要通过非迭代的方法求解最优滤波器,借此提取连续的周期性脉冲信号,克服了迭代过程中获取的滤波器可能不是全局最优滤波器的缺点,但MOMEDA需要提前设置其滤波器尺寸和周期范围,每次只能提取单一的周期性冲击,且在强噪音背景下,此方法对故障信号的提取并不理想[19-20]。

基于上述旋转机械故障诊断现状,本文提出一种基于多元变分模态分解和多点最优最小熵反褶积(MVMD-MOMEDA)的信号处理方法,以解决在单一通道问题上无法处理多源信号以及早期微弱故障特征难以提取等问题。该方法通过多源振动信号的融合分析,得到一系列IMF分量并引入无量纲峭度参数进行信号的重构,在解决IMF分量选取问题的基础上达到降噪的目的,并结合改进多元最优最小熵反褶积的故障特征提取方法,有效识别信号中故障冲击成分。

1 MVMD-MOMEDA方法

1.1 多元变分模态分解(MVMD)

多元变分模态分解是在VMD的基础上进行多源数据的广义扩展研究,其主要目标是从包含C个数据通道的多元输入信号x(t)中提取预定义的K个多元调制振荡信号:

(1)

式中uk(t)=[u1(t),u2(t),…,uC(t)]。

(2)

式中:{uk,c(t)}为信道C中的调制振荡信号的集合;{ωk}为中心频率的集合。

上述模型中多个线性等式约束对应于通道的总数。相应的增广拉格朗日函数变成:

(3)

式中:α为惩罚因子;λc(t)为拉格朗日乘子;〈〉表示内积。

针对式(3)的复杂变分优化问题,利用乘子交替方向法(alternate direction method of multipliers,ADMM)来求解,借此迭代更新uk(t)、ωk和λc,求解变分优化问题的最优解。

其中,模态更新关系为

(4)

中心频率更新关系为

(5)

1.2 多点最优最小熵反褶积

MOMEDA是改进的最小熵反褶积(minimum entropy deconvolution,MED),提供多个脉冲反褶积目标而非单个脉冲目标,克服了MED算法错误的卷积杂散的脉冲和求解迭代的缺陷,主要应用于周期脉冲的故障特征提取。其通过寻求一个最优解卷积滤波器f(f=(f1,f2,…,fL),其中L为滤波器长度),来求解多点D范数MDN的最大值,从而获得MOMEDA。

(6)

(7)

式中t表示一个恒定矢量,用于描述目标脉冲的位置和权重。

t1M1+t2M2+…+tN-LMN-L=X0y。

(8)

(9)

(10)

为了准确提取故障特征,引入多点峭度(Mkurt)作为特征提取的度量标准。

(11)

式中:y为输出信号;t为目标向量;N是输入信号的长度;L是滤波器的长度。

该定义是基于峭度提出的,但目标向量扩展到受控位置处的多个脉冲。实际上,每个故障周期信号中,不一定只存在1个冲击成分,多点峰值所对应的故障周期并不是只有1个。当多点峭度达到峰值时,该峰值对应的采样总数可能是故障的整数倍或半整数倍,至此来完成故障周期的确定。

1.3 基于MVMD-MOMEDA的诊断步骤

MVMD-MOMEDA算法在齿轮箱故障诊断中的具体实现步骤如下:

1)采用多个加速度传感器获取齿轮箱故障振动信号;

2)将采集到的多通道振动信号进行融合,利用MVMD算法对其进行分解;

3)以无量纲参数峭度(Ku)为指标,选择其阈值附近包含故障信息较多的IMF进行重构,从而剔除噪声分量的干扰,使原始信号中的有效成分大幅度的保留出来;

4)对重构信号进行多点峭度谱分析,确定故障周期成分;

5)根据不同的故障特征频率设置采样区间,进行MOMEDA解卷积处理,寻求最优滤波器,对冲击信号进行恢复;

6)根据求解后的故障特征图,将主导故障特征频率及其倍频和理论计算值进行分析对比,判别故障发生的类型。

故障诊断流程图如图1所示。

图1 基于MVMD-MOMEDA的故障诊断流程图

2 仿真信号分析

2.1 MVMD仿真验证

MVMD的优点在于可同时分解多通道信号,且不会出现模态混叠的情况。现设置含高斯白噪声的仿真信号验证其分解的优越性,仿真信号如下:

(12)

式中:x1为频率25 Hz、幅值5的正弦信号;x2为频率50 Hz、幅值10的余弦信号;x3为频率100 Hz、幅值20的正弦信号;ζ为模拟信号的高斯白噪声。各个信号和合成信号的时域波形图如图2所示。

图2 仿真信号时域波形图

将合成不加白噪声的仿真信号x进行MVMD分解,得到预设的K=3个本征模态函数(IMF)分量,每个IMF分量的时域图和频域图如图3 a)所示。由图3 a)可知,被分解出来的IMF1—IMF3很清晰地还原了输入信号,包含了每个正余弦函数的频率成分,频谱上每条仿真信号的频率分别为25,50和100 Hz,与预设的频率相吻合且并没有丢失原始信号的频率特征,说明MVMD信号分解的有效性与准确性。

图3 仿真信号分解图

现将含有“10 dB”高斯白噪声的合成信号“x-ζ”进行MVMD分解,得到预设的K=3个IMF分量,每个IMF的时域图和频域图如图3 b)所示。由图3 b)可知,噪声的存在直接影响了信号在时域上的规律分布性,在IMF1中25 Hz和50 Hz被反映了出来,且具有很强的能量幅值,在IMF2中含有微弱的50 Hz和100 Hz的频率,IMF3则直接淹没了全部的频率成分,说明分解过后的模态函数中,IMF1和IMF2可以有效地表示输入仿真信号,而IMF3则包含太多噪声,不能清晰地表示输入信号,在IMF的选择中可以直接剔除掉,留下IMF1和IMF2表示输入信号,MVMD的信号处理方法就达到了目的,即信号分解重构后完成降噪。为进一步验证MVMD的有效性,将含有“10 dB”噪声的合成信号“x-ζ”进行EMD分解,如图3 c)所示,分解出的3个IMF分量中,并不能有效提取出包含原始信号频率特征的信息。

2.2 MOMEDA仿真验证

MOMEDA对脉冲信号的敏感性使得其从故障信号中可以有效地提取到故障脉冲冲击。应用故障冲击信号来验证该算法的有效性,信号x1(t)是一个幅值为1的正弦波;信号x2(t)为幅值2、故障周期70的强冲击信号;信号x3(t)为幅值4、故障周期100的弱冲击信号;信号x(t)为无噪声的仿真合成信号。仿真信号如图4所示。

图4 MOMEDA仿真信号时域波形图

虽然在信号x(t)中可以看到传递信号中包含了部分冲击成分,但无法判断冲击的具体频率,求解合成信号的多点峭度图以判断冲击成分。信号x(t)的多点峭度图如图5 a)所示。

图5 MOMEDA验证图

在合成信号多点峭度图中可以明显观察到在周期35,70,140等处存在多点峭度峰值,对应强冲击信号的半数倍和整数倍;在周期50,100,200,250等处同样存在明显的峰值,对应弱冲击信号的半数倍和整数倍。对比无冲击信号成分的仿真信号(“2.1”中的无噪声仿真信号)多点峭度图如图5 b)所示。图5 b)中并没有任何的峰值波动,由此可以判断多点峭度图可以很好地识别信号中的冲击成分,并以多点峭度峰值的方式展现在波形图中,进而应用MOMEDA算法进行故障频率的增强。为了更好地展示MOMEDA的有效性,设置周期区间[90,110],对弱冲击信号的故障周期进行增强,增强结果如图5 c)所示,表明故障周期的增强有利于故障频率更好的识别。

3 实验验证与分析

本文使用的数据来源于QPZZ-Ⅱ试验台,如图6所示。该试验台可以快速模拟旋转机械多种状态,并进行状态分析和诊断。该试验台由变速驱动电机、轴承、齿轮箱、调速器等组成,通过调节配重、部件的安装位置以及组件的有机组合快速模拟各种故障,为验证本文所提算法的有效性提供了真实的齿轮箱实验数据。

该实验台齿轮箱齿轮为直齿轮,输入轴小齿轮齿数Z1=55,输出轴大齿轮齿数Z2=75,采样频率FS=5 200 Hz,该实验包含4个通道的采集信号,分别是输入轴的电机侧和负载侧及输出轴的电机侧和负载侧。将传感器分别置于齿轮箱箱体外侧,由于距离振源较远,且采集过程中不可避免的存在外界噪声的干扰,借此来模拟复杂传递路径、强背景噪声影响下齿轮箱振动信号的采集。齿轮工况分别为健康状态、输出轴大齿轮断齿和输入轴小齿轮磨损3种,如图7所示。驱动电机转速为n=880 r/min,故障频率如表1所示。

表1 故障特征频率计算结果

图7 齿轮工况

现选取QPZZ-Ⅱ试验台测得的0负载下880 r/min的3种工况的齿轮实测信号进行分析验证,每种工况包含4个通道的采集信号,每个样本信号采样5 120点,时长1.0 s。每种工况的不同通道的时域波形图如图8所示。

图8 3种齿轮工况多通道时域波形图

将采集到的每种工况不同通道的振动信号进行融合后,对信号进行MVMD分解,此时需要预设分解层数K,K值直接影响MVMD分解信号的效果,通过读取分解出的每个IMF的中心频率和带宽是否发生混叠可以判断分解层数的合理性。表2和表3给出K=3—7层的中心频率和频率带宽。

表2 不同K值的中心频率

表3 不同K值的中心频率对应的带宽

由表2可知,当K=3和4时,IMF分量的中心频率并没有完全表现出来,对应表3可知,中心频率对应的带宽出现空挡,说明信号还欠分解,每个分量并没有完全表示出原始信号的频率特征成分,且随着K值的增大、IMF增多,每个分量都包含原始信号的频率特征,直至K=6和7时,IMF5和IMF6的分量中心频率相差开始变得并不均匀,且对应表3可知,IMF中心频率对应的频带带宽开始出现重叠,说明信号出现了过分解现象,对比分析可知,当K=5时,信号达到完全分解,且频带分布合理。现将不同工况的信号进行MVMD分解,采用中心频率判别法预设分解层数K=5,惩罚系数α=2 000,各个工况的时域图和频谱图如图9所示。

图9 不同工况MVMD分解的时域图和频谱图

现统计各个IMF分量的峭度值(Ku)来选择IMF进行信号重构,降低信号中的噪声成分,使得信号中的冲击成分更加清晰,各IMF分量峭度值如表4所示。Ku值越大,说明齿轮的故障越严重,根据峭度值可以判断IMF3—IMF5的数值远超峭度阈值,继而进行信号的重构,得到降噪后原始信号的时域图和频谱图如图10所示。

表4 各个IMF分量峭度值

图10 重构信号的时域图和频谱图

重构信号相比原始采集信号在时域图上有明显的降噪效果且频率成分更加清晰。将重构后的降噪信号进行多点峭度图求解,识别信号中的冲击频率,然后进行MOMEDA求解,得到增强的故障信号以读取信号中的故障特征。

如图11 a)所示,冲击频率及其倍频在多点峭度图中被提取出来。将故障信号进行MOMEDA求解,设置采样区间为[470,490],滤波长度L=800,得到求解过后的故障特征图,在结果图中可以清晰地观察到周期频率的存在,与大齿轮的故障特征频率476.3 Hz相对应,因此判断该信号为大齿轮的故障信号。同理,设置图11 b)中采样区间为[340,360],滤波长度L=800,得到求解过后的故障特征图周期频率与小齿轮的故障特征频率348.3 Hz相对应,因此该信号为小齿轮的故障信号。验证了使用MVMD-MOMEDA能够准确地提取齿轮箱故障特征频率。

图11 多点峭度图和MOMEDA求解结果

为进一步证明本文所提方法的有效性,将直接采集到的大齿轮断齿故障信号进行MOMEDA解卷积计算,求解结果如图12所示。从图12可以看出,由于没有对采集到的振动信号进行降噪预处理及多点峭度图分析,所提取到的故障特征周期频率并不能有效地对应大齿轮故障周期。因此,针对齿轮箱故障信号处理,本文所提方法具有一定的可靠性和有效性。

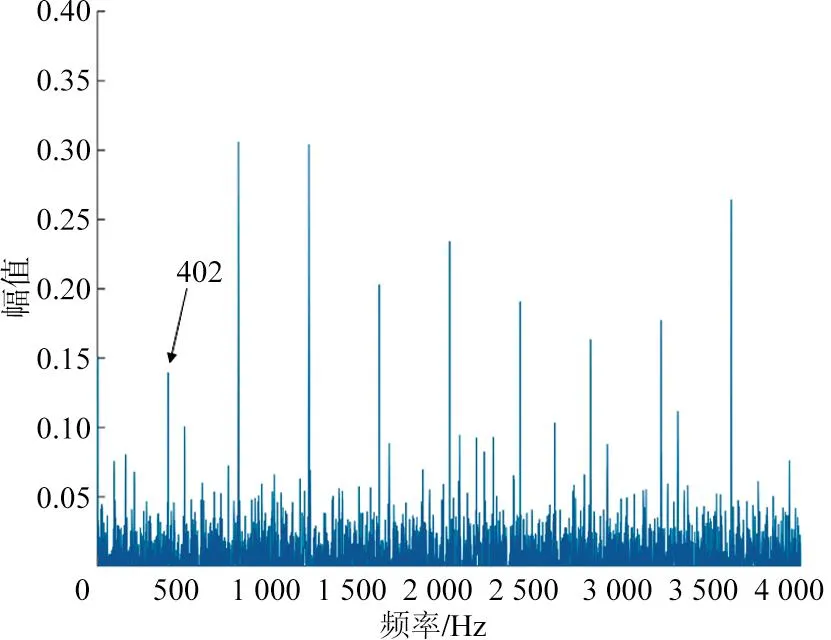
图12 MOMEDA解卷积结果

4 结 论

本文提出了一种基于MVMD-MOMEDA的齿轮箱故障诊断方法,对仿真信号和实验数据进行了分析验证,得出以下结论。

1)MVMD算法包含了VMD算法的所有优点,解决了EMD算法中模态混叠和虚假分量的缺陷,在多元信号方面优化了VMD算法的单通道信号处理的单一性。

2)对多通道融合后的振动信号进行MVMD分解,应用中心频率判别法选择IMF分量的分解层数,并引入无量纲参数峭度选择IMF分量进行信号重构,得到降噪后的实验信号,为后续MOMEDA算法特征提取做信号预处理。

3)对重构信号进行MOMEDA分析以提取特征,在特征识别结果中有效识别到故障信号和故障类型信号,证明MOMEDA算法的有效性。通过仿真信号和实验信号验证了基于MVMD-MOMEDA的齿轮箱故障诊断方法的优越性。

本文不足之处在于仅针对多传感器采集到的振动信号进行了融合分析,下一步将针对振动、油温、转速等异类信息融合下的齿轮箱健康状态与故障诊断进行研究,充分利用信号间的互补来丰富故障特征信息。

参考文献/References：

[1] 王朝阁,李宏坤,曹顺心,等.改进VMD和非凸重叠组收缩降噪的行星齿轮箱早期故障特征提取[J].振动工程学报,2021,34(6):1293-1304.

WANG Chaoge,LI Hongkun,CAO Shunxin,et al.Incipient fault feature extraction of planetary gearbox based on modified VMD and non-convex overlap group shrinkage denoising[J].Journal of Vibration Engineering,2021,34(6):1293-1304.

[2] 胡爱军,严家祥,白泽瑞.基于MOMEDA和增强倒频谱的风电机组齿轮箱多故障诊断方法[J].振动与冲击,2021,40(7):268-273.

HU Aijun,YAN Jiaxiang,BAI Zerui.Multi-fault diagnosis method for wind turbine gearbox based on MOMEDA and enhanced cepstrum[J].Journal of Vibration and Shock,2021,40(7):268-273.

[3] LI Zhuorui,MA Jun,WANG Xiaodong,et al.MVMD-MOMEDA-TEO model and its application in feature extraction for rolling bearings[J].Entropy,2019,21(4).DOI:10.3390/e21040331.

[4] 王志坚,韩振南,宁少慧,等.基于CMF-EEMD的风电齿轮箱多故障特征提取[J].电机与控制学报,2016,20(2):104-111.

WANG Zhijian,HAN Zhennan,NING Shaohui,et al.Wind turbine gearbox multi-fault diagnosis based on CMF-EEMD[J].Electric Machines and Control,2016,20(2):104-111.

[5] 梁子寅,刘向东,卢宗慧,等.滚动轴承故障诊断分析方法研究综述[J].制造业自动化,2023,45(5):172-175.

LIANG Ziyin,LIU Xiangdong,LU Zonghui,et al.A review of research on rolling bearing fault diagnosis and analysis methods[J].Manufacturing Automation,2023,45(5):172-175.

[6] 赵磊,张永祥,朱丹宸.复杂装备滚动轴承的故障诊断与预测方法研究综述[J].中国测试,2020,46(3):17-25.

ZHAO Lei,ZHANG Yongxiang,ZHU Danchen.Review on rolling bearing fault diagnosis and prognostic for complex equipment[J].China Measurement&Testing Technology,2020,46(3):17-25.

[7] 史红梅,郑畅畅,司瑾,等.基于动态加权的多尺度残差网络旋转机械故障诊断算法[J].振动与冲击,2022,41(23):67-74.

SHI Hongmei,ZHENG Changchang,SI Jin,et al.Fault diagnosis algorithm of rotating machinery based on dynamic weighted multiscale residual network[J].Journal of Vibration and Shock,2022,41(23):67-74.

[8] 唐振宇,黄凯,杨期江,等.基于相关系数稀疏表征的转子振动信号周期特征提取[J].机床与液压,2022,50(17):200-205.

TANG Zhenyu,HUANG Kai,YANG Qijiang,et al.Periodic feature extraction of rotor vibration signal based on sparse representation of correlation coefficient[J].Machine Tool&Hydraulics,2022,50(17):200-205.

[9] 杜煜坤,徐乐,魏语辰,等.滚动轴承故障诊断发展现状及发展趋势[J].设备管理与维修,2022(11):128-129.

[10] 梁春辉,刘晓波.VNCMD结合Birge-Massart阈值降噪的航空发动机转子故障诊断[J].机械设计与制造,2023(4):201-205.

LIANG Chunhui,LIU Xiaobo.Fault diagnosis of aeroengine rotor based on VNCMD and Birge-Massart threshold denoising[J].Machinery Design &Manufacture,2023(4):201-205.

[11] FLANDRIN P,RILLING G,GONCALVES P.Empirical mode decomposition as a filter bank[J].IEEE Signal Processing Letters,2004,11(2):112-114.

[12] 赵进平.异常事件对EMD方法的影响及其解决方法研究[J].青岛海洋大学学报,2001,31(6):805-814.

ZHAO Jinping.Study on the effects of abnormal events to empirical mode de-composition method and the removal method for abnormal signal[J].Journal of Ocean University of Qingdao,2001,31(6):805-814.

[13] DRAGOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing,2014,62(3):531-544.

[14] 刘迎松,魏志刚,束海星,等.基于参数自适应VMD和MCKD的滚动轴承微弱故障特征提取[J].噪声与振动控制,2023,43(3):102-109.

LIU Yingsong,WEI Zhigang,SHU Haixing,et al.Weak fault feature extraction of rolling bearings based on parameter adaptive VMD and MCKD[J].Noise and Vibration Control,2023,43(3):102-109.

[15] 毕浩程,蒋章雷,吴国新,等.基于SSA-VMD和2.5维谱的齿轮箱磨损故障诊断[J].机床与液压,2023,51(6):181-187.

BI Haocheng,JIANG Zhanglei,WU Guoxin,et al.Gearbox wear fault diagnosis based on SSA-VMD and 2.5-dimensional spectrum[J].Machine Tool&Hydraulics,2023,51(6):181-187.

[16] 杨铮鑫,王明罡,党鹏飞,等.基于VMD-HT的滚动轴承故障诊断[J].机械设计与制造,2023(3):15-18.

YANG Zhengxin,WANG Minggang,DANG Pengfei,et al.Fault diagnosis of rolling bearing based on feature extraction of VMD-HT[J].Machinery Design &Manufacture,2023(3):15-18.

[17] UR REHMAN N,AFTAB H.Multivariate variational mode decomposition[J].IEEE Transactions on Signal Processing,2019,67(23):6039-6052.

[18] MCDONALD G L,ZHAO Qing.Multipoint optimal minimum entropy deconvolution and convolution fix:Applicationto vibration fault detection[J].Mechanical Systems and Signal Processing,2017,82:461-477.

[19] 王志坚,张纪平,王俊元,等.基于MED-MOMEDA的风电齿轮箱复合故障特征提取研究[J].电机与控制学报,2018,22(9):111-118.

WANG Zhijian,ZHANG Jiping,WANG Junyuan,et al.Wind turbine gearbox multi-fault diagnosis based on MED-MOMEDA[J].Electric Machines and Control,2018,22(9):111-118.

[20] 陈丙炎,宋冬利,张卫华,等.改进MOMEDA方法及其在滚动轴承故障特征增强中的应用[J].机械强度,2021,43(1):1-8.

CHEN Bingyan,SONG Dongli,ZHANG Weihua,et al.Improved MOMEDA method and its application to fault feature enhancement of rolling element bearings[J].Journal of Mechanical Strength,2021,43(1):1-8.