具有Holling IV功能性反应和非线性收获的随机捕食-食饵模型

叶 葱，魏春金，张树文

(集美大学理学院，福建 厦门 361021)

0 引言

长期以来，在种群动力系统中，捕食与食饵模型是许多学者一个重要的研究方向，在此方面也取得了大量丰富的成果[1-5]。文献[6]提出了模型

(1)

其中：x(t)、y(t)分别表示食饵和捕食者在t时刻的种群密度；a1>0、a2>0分别表示食饵和捕食者的内禀增长率；b>0表示食饵种群的密度制约系数；f1y(t)/(c1+nx(t)+x2(t))为Holling IV功能反应函数；f2y(t)/(c2+x(t))表示具有Leslies形式的捕食者数量反应。近年来，学者们开始关注收获对捕食-食饵系统动力学的影响，并完成了大量的工作。在捕食-食饵系统的动力学中，收获函数起到了非常关键的作用。文献[7]提出了常数收获、比例收获、非线性收获3种类型的收获功能，其中非线性收获比常数收获和比例收获更具有现实性。然而，在现实世界中，随机干扰是处处存在的，种群在环境中会受到各种随机干扰的影响[8-10]。因此，与确定性模型相比，随机模型更具有真实性。受文献[11]的启发，本文在模型(1)的基础上获得随机模型

(2)

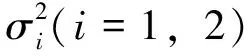
另一方面，周期现象在实际的生态系统中是普遍存在的，因为种群中的个体受生命周期、季节变化以及昼夜更替等影响，该物种的出生率、死亡率和其他参数都呈现出周期变化[12]。因此，考虑周期因素对相应的动力学系统行为的影响显得尤为重要。所以，相应系统(2)的非自治系统为

(3)

其中：a1(t)、b(t)、f1(t)、c1(t)、n(t)、p1(t)、m1(t)、σ1(t)、a2(t)、f2(t)、c2(t)、p2(t)、m2(t)、σ2(t)均为正的、有界的、连续的正w周期函数。

1 预备知识

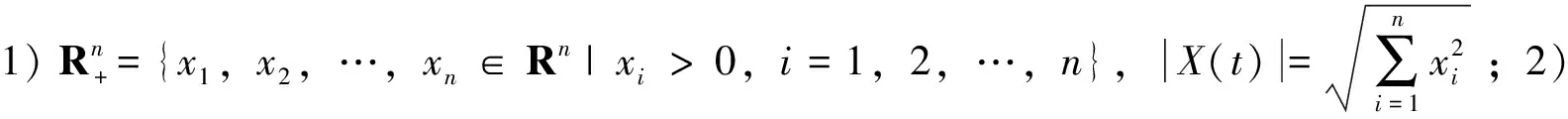
随机微积分方程

dx(t)=f(x(t)，t)dt+g(x(t)，t)dB(t)

(4)

的解记作x(t)=(x1(t)，x2(t)，…，xn(t))(t≥0)，其中f∈L1(Rn×R+，Rn)，g∈L2(Rn×R+，Rn×m)，B(t)是n维布朗运动。

定理1[13](存在唯一性定理) 假设f(x(t)，t)和g(x(t)，t)关于x(t)满足下列条件：1)局部Lipschitz条件，存在ck>0(k=1，2，…)，使得∀x，y∈Rn且|x|∨|y|≤k，有不等式|f(x，t)-f(y，t)|∨|g(x，t)-g(y，t)|≤ck|x-y|成立；2)线性增长条件，存在c>0，使得|f(x，t)|∨|g(x，t)|≤c|1+|x||，∀(x，t)∈Rn×R+，则初始条件为x(0)=x0∈Rn的系统(4)存在唯一连续的局部解x(t)(t∈[0，τe))，τe是爆破时间。

定理2[13](It公式) 设x(t)(t≥0)是It过程，其随机微分为dx(t)=f(t)dt+g(t)dB(t)，其中，f∈L1(R+，Rn)，g∈L2(R+，Rn×m)。若V(x(t)，t)∈C2，1(Rn×R+；R)，则V(x(t)，t)仍然是It过程，具有随机微分dV(x(t)，t)=Vt(x(t)，t)dt+Vx(x(t)，t)dx(t)+dxT(t)Vxx(x(t)，t)dx(t)/2。

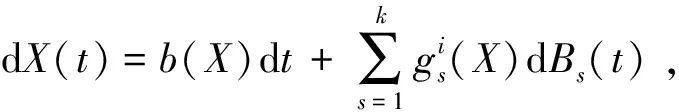
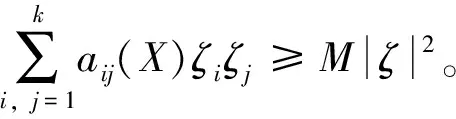
为了验证性质2成立，只要证明存在非负的C2-函数及邻域U，使得对于任意的X∈ElU，LV(X)是负的。

下面考虑方程

(5)

假设方程(5)的系数b(s，X(s))、σr(s，X(s))(r=1，2，…，k)满足条件

(6)

(7)

其中：B是一个常数。

2 主要结果及其证明

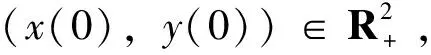
证明首先考虑方程

(8)

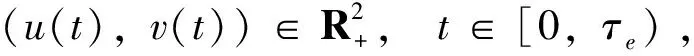
令k0>0足够大，使得(x(t)，y(t))∈[1/k0，k0]×[1/k0，k0]，对于任意的正数k≥k0，定义一个停时序列τk=inf{t∈[0，τe)：x(t)(1/k，k)或y(t)(1/k，k)}。

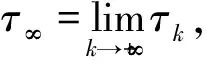
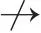
通过不等式y≤2(y-1-lny)+ln 4≤2V(x，y)+ln 4，可得LV(x，y)≤N1+(a2+f2/c2+f1/c1)ln 4+2(a2+f2/c2+f1/c1)V(x，y)≤N2(1+V(x，y))，其中，N2=max{N1+(a2+f2/c2+f1/c1)ln 4，2(a2+f2/c2+f1/c1)}，所以有

dV(x，y)≤N2(1+V(x，y))dt+(x-1)σ1x/(1+m1x)dB1+(y-1)σ2x/(1+m2x)dB2。

(9)

对式(9)从0到τk∧T1进行积分可得

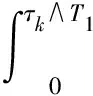
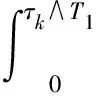
通过Gronwall不等式，得EV[x(τk∧T1)，y(τk∧T1)]≤(V[x(0)，y(0)]+N2T)eN2T。

后续证明与文献[19]类似，在此省略。

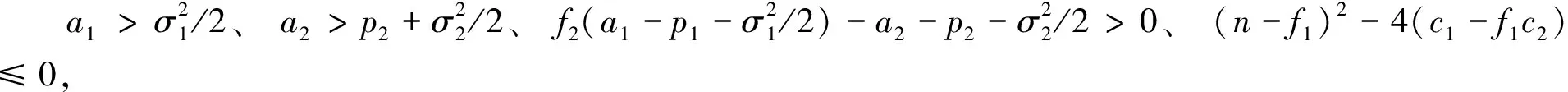
证明首先考虑方程

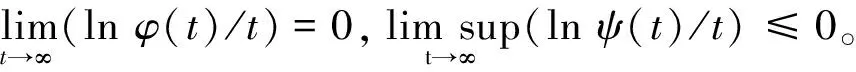
接下来，考虑食饵种群x(t)。应用It公式可得

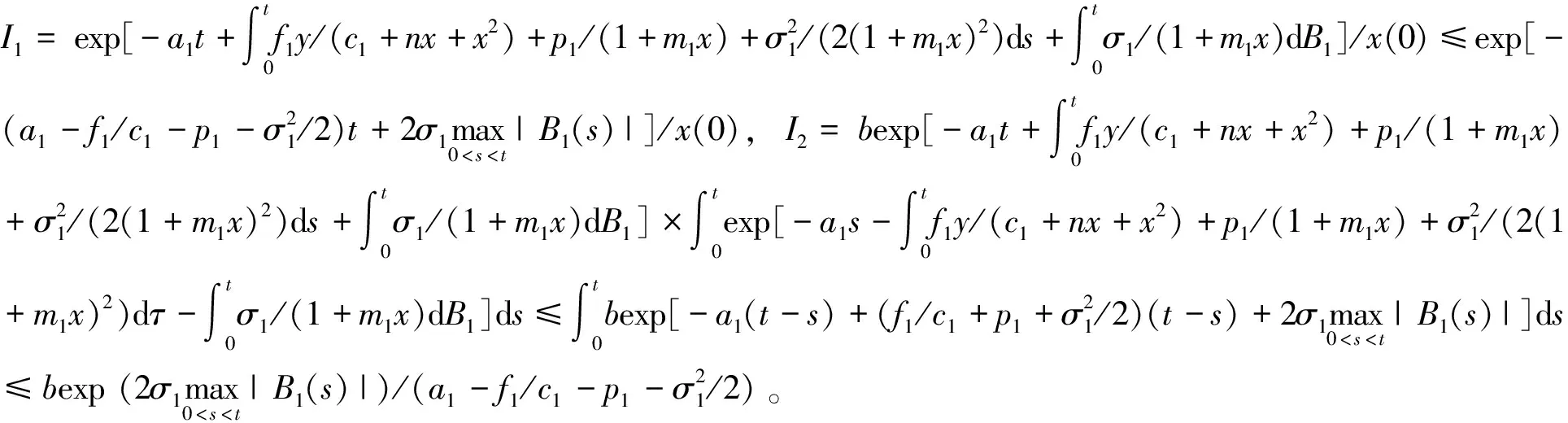
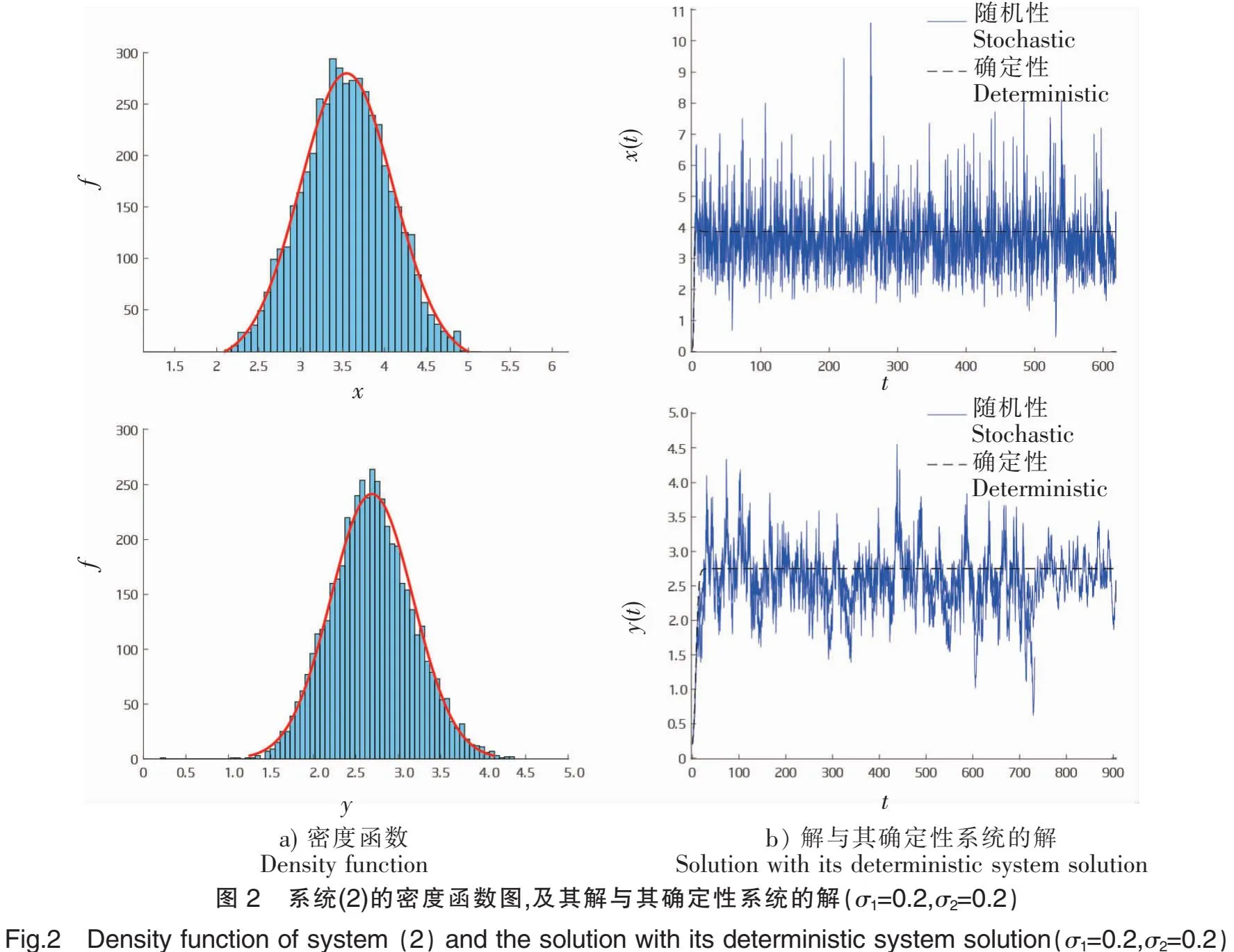
定义一个Lyapunov函数lnx，通过It公式得，又因为f1y/(c1+nx+x2)=y/(c1/f1+n/f1+x2/f1)。比较c1/f1+n/f1+x2/f1与c2+x的大小，c1/f1+n/f1+x2/f1-(c2+x)=(x2+(n-f1)x+c1-f1c2)/f1，所以Δ=(n-f1)2-4(c1-f1c2)。

(10)

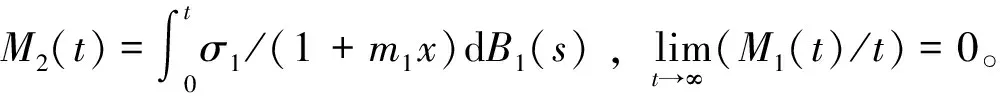
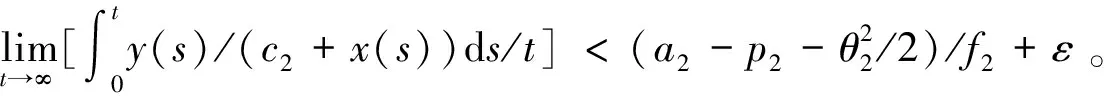
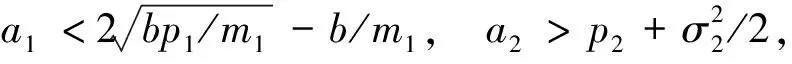
证明i)定义Lyapunov函数lnx，由It公式得，对上述不等式两边从0到t进行积分，并同时除以t，得即因此，对于任意小的ε>0，存在t0和一个集合Ωε，使得对t>t0和ω∈Ωε，都有P(Ωε)≥1-ε和x(t)/(c2+x(t))≤ε成立。由等式dy=y[a2-f2y/(c2+x)-p2/(1+m2y)]dt-σ2y/(1+m2y)dB2(t)=y[a2-f2y/c2+f2yx/((c2+x)c2)-p2/(1+m2y)]dt-σ2/(1+m2y)dB2(t)，可得y[a2-f2y/(c2+x)-p2/(1+m2y)]dt-σ2y/(1+m2y)dB2(t)≤dy≤y[a2-f2y/c2+εf2y/c2-p2/(1+m2y)]dt-σ2y/(1+m2y)dB2(t)。

对任意的ε>0，有

dy=y[a2-f2y/(c2+x)-p2/(1+m2y)]dt-σ2y/(1+m2y)dB2(t)。

(11)

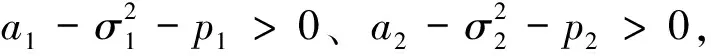
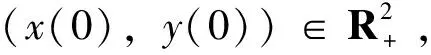
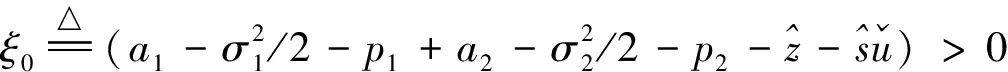
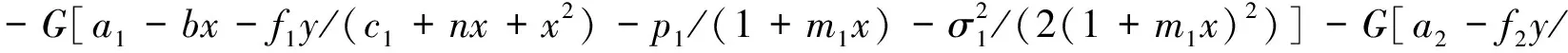
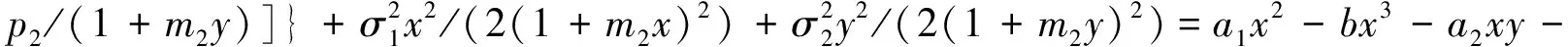
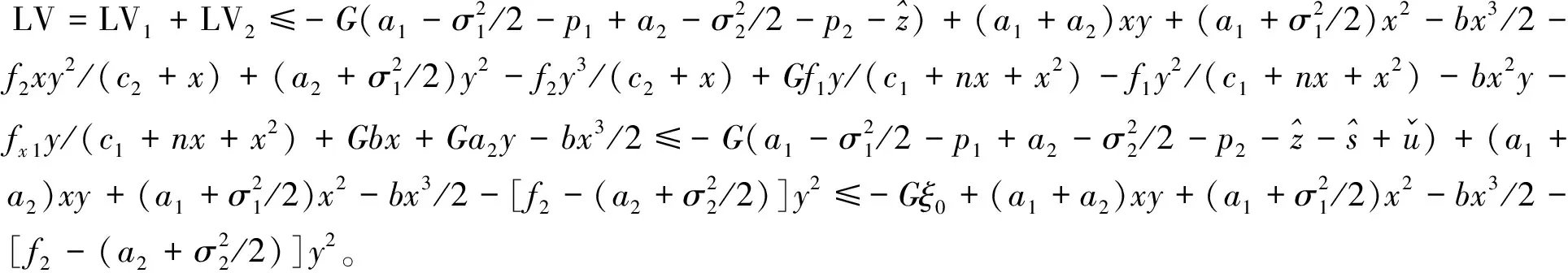
(12)

(13)

(14)

(15)

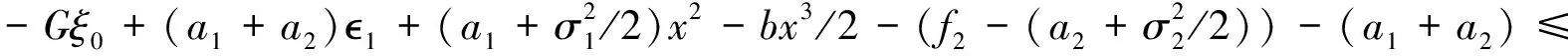
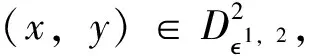
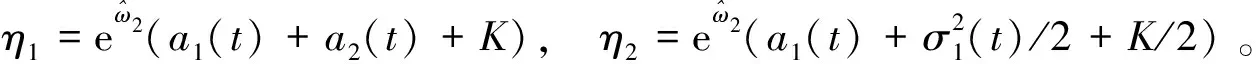
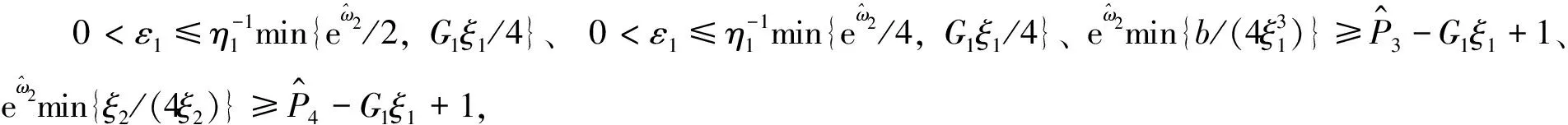
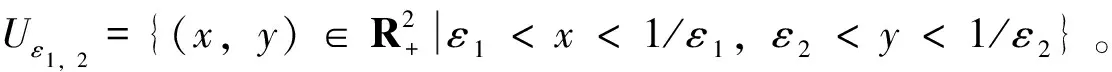
3 数值模拟结果

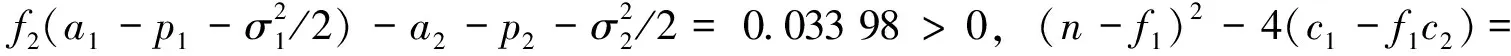
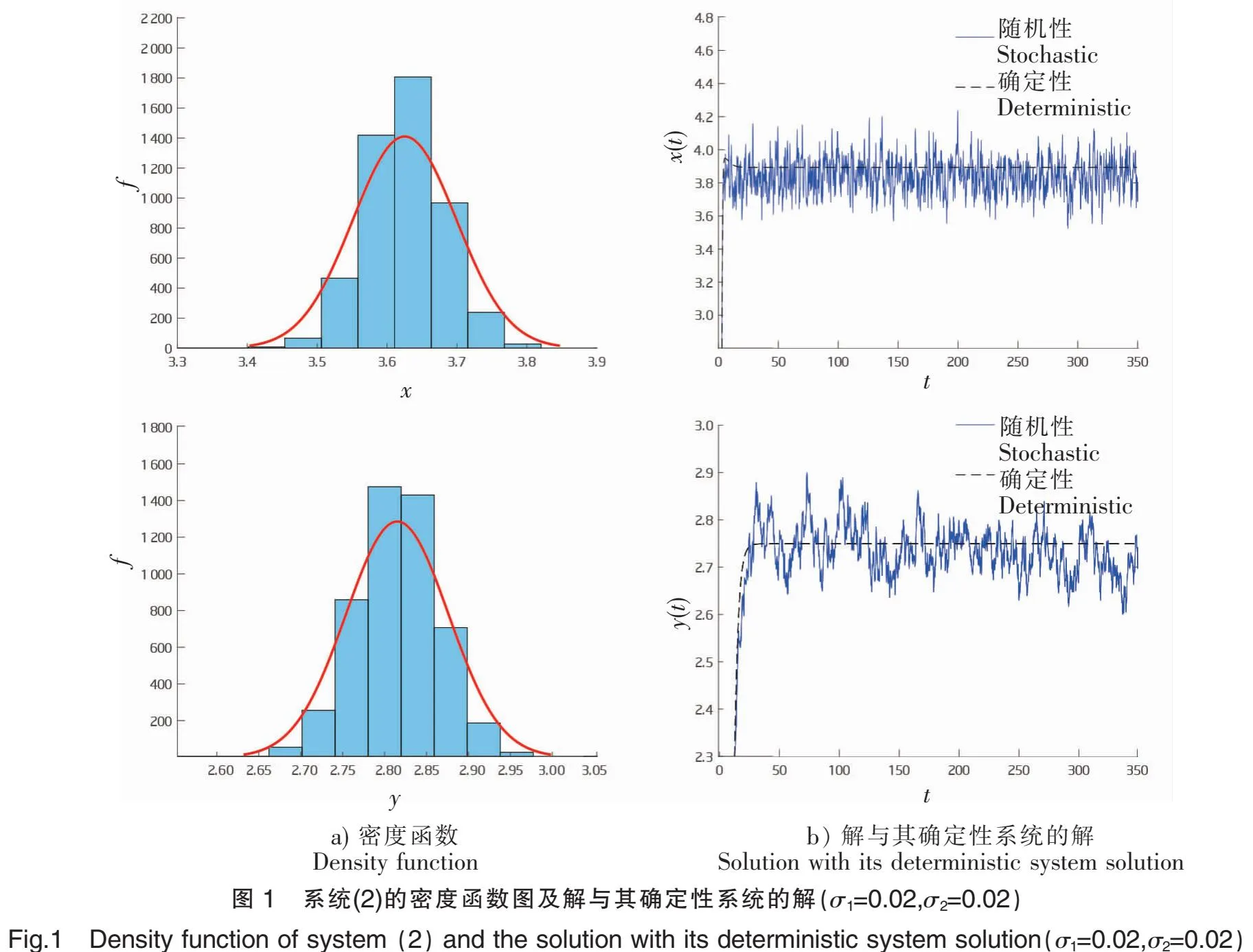
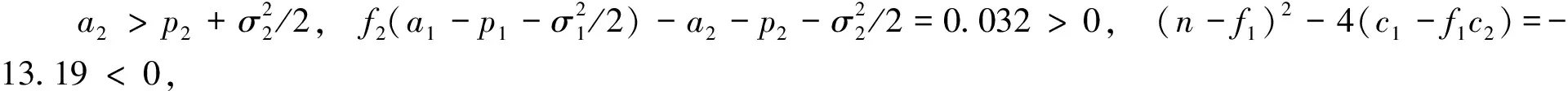
对于随机模型(2)，首先取初值x=0.1，y=0.2。选择适当参数：a1=0.4，b=0.1，m1=1/6，m2=1/6，f1=0.1，a2=0.4，f2=1.1，c2=5，c1=4，n=1，p1=0.6，p2=0.6，σ1=0.2，σ2=0.2。通过计算，显然满足定理5的条件ii)。由图3可以看出，食饵x与捕食者y均灭绝，说明过度捕获将导致种群减少。

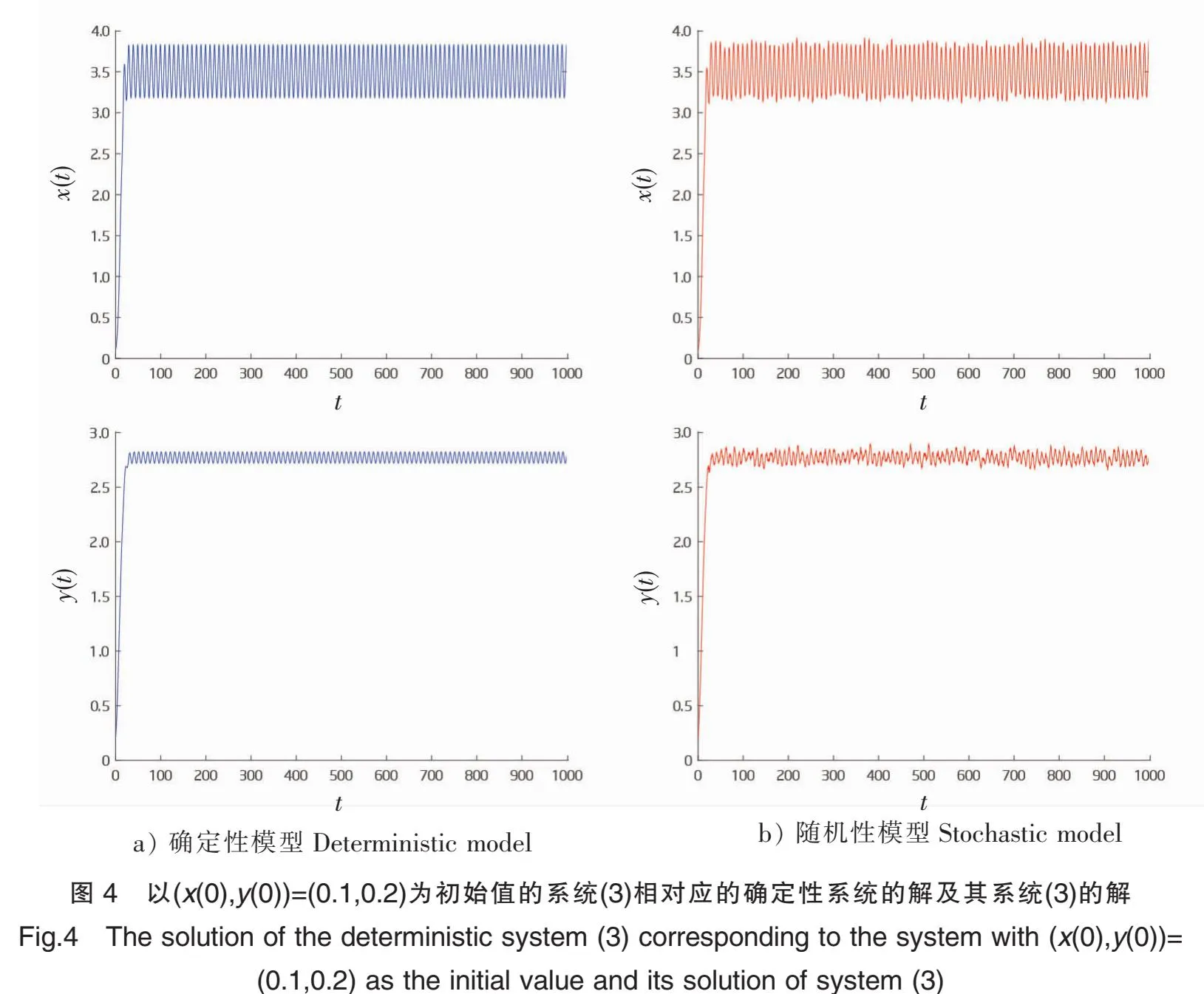
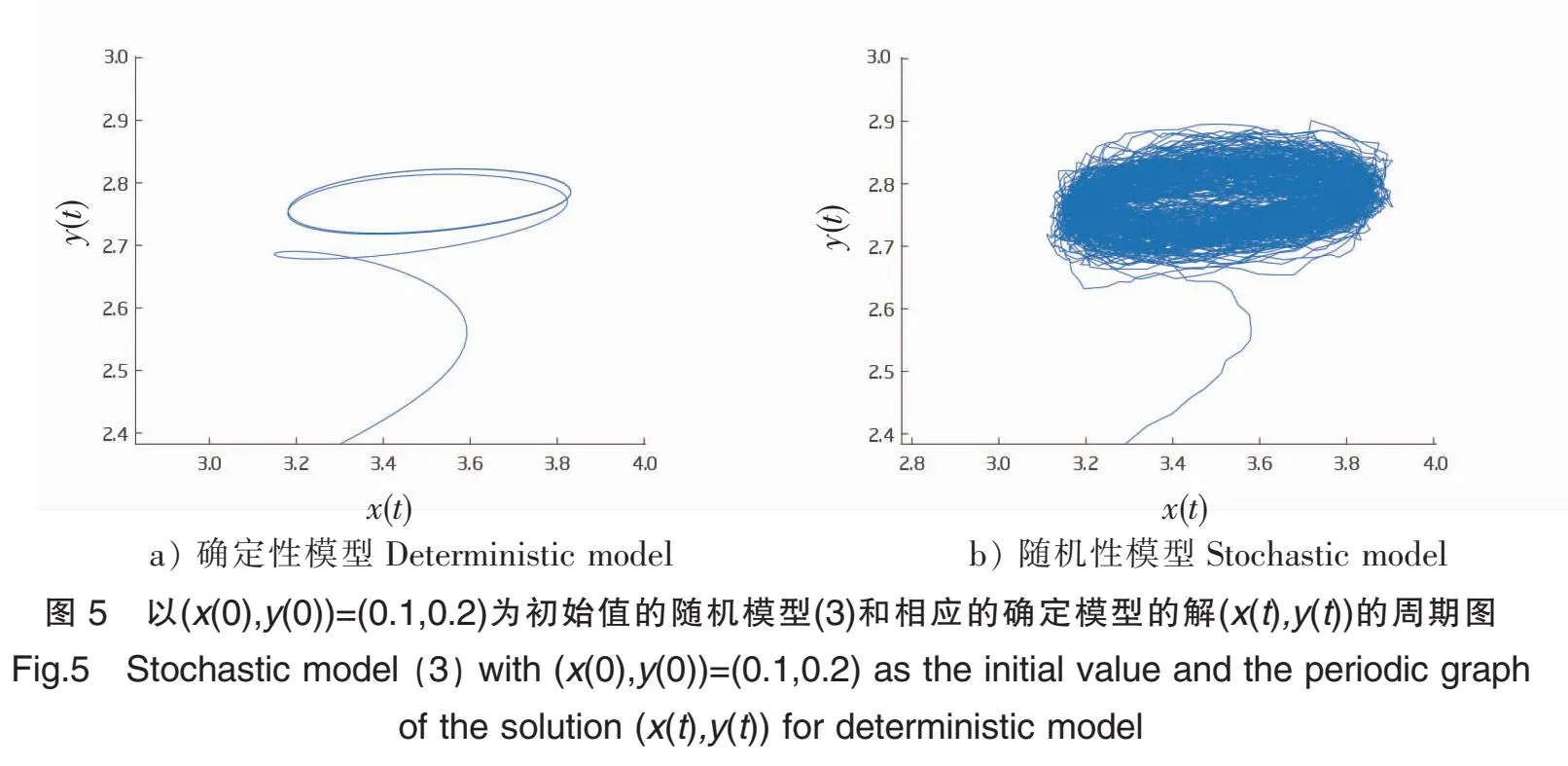
对于随机模型(3)，首先取初值x=0.1，y=0.2。选择适当参数：a1=0.4+0.02sin(πt/5)，b=0.1+0.02sin(πt/5)，m1=1+0.02sin(πt/5)，m2=1+0.02sin(πt/5)，f1=0.1+0.02sin(πt/5)，a2=0.4+0.02sin(πt/5)，f2=1.1+0.02sin(πt/5)，c2=5+0.02sin(πt/5)，c1=4+0.02sin(πt/5)，n=1+0.02sin(πt/5)，p1=0.06+0.02sin(πt/5)，p2=0.06+0.02sin(πt/5)，σ1=0.01+0.001sin(πt/5)，σ2=0.01+0.001sin(πt/5)，显然符合定理7的ξ1>0、ξ2>0条件。由定理7可以看出，系统(3)至少存在一个周期解，这意味着捕食者和食饵种群将长期共存并表现出周期性。由图4和图5可以看出，对于任何正的初始值，确定性模型的解将在一段时间后进入周期轨道，而当噪声强度较小时，随机模型(3)的解会在周期轨道的小范围内振动。

模拟结果说明，环境噪声强度和可捕获性对随机捕食-食饵模型有重要的影响。

4 结论

本文研究了具有Holling IV功能性反应和非线性收获的随机捕食-食饵系统。证明了对于任意给定的初始值，系统(2)都存在唯一的全局正解；得到了系统(2)的平均持续生存与灭绝的充分条件。此外，在满足一定条件下，使用Has’minskii的平稳分布理论及周期性理论，得到了系统(2)存在唯一的平稳分布且具有遍历性，并获得了系统(3)存在非平凡的正周期解。