具有恐惧效应的随机捕食-食饵模型动力学

李 江，魏春金

(集美大学理学院，福建 厦门 361021)

0 引言

长期以来，在种群动力系统中，捕食与食饵模型是许多学者的一个重要研究方向，这方面的研究也取得了大量丰富的成果[1-7]。生态学研究主要关注的是捕食者与食饵之间的相互作用，这种相互作用主要是由捕食者对食饵的直接消耗控制的。文献[8]提出了模型

(1)

其中：x(t)、y(t)分别表示食饵和捕食者在t时刻的种群密度；c为转化率；f1(x(t))、f2(y(t))分别表示食饵和捕食者的增长率；p(x(t)、y(t))为功能反应函数。然而，最新的理论研究和实验结果表明，除了直接捕食之外，捕食者的间接效应也会显著改变整个生态系统的动力学[9-11]。仅仅是捕食威胁就足以迫使食饵改变自身的生活习惯并表现出各种反捕食的行为，如选择新的栖息地、改变觅食时间和寻找更安全的觅食地点等，这也会使得食饵生长、生存和繁殖的能力下降[12-15]。基于此，文献[16]考虑捕食者引起的恐惧并建立了模型

(2)

其中：f(k,y)为恐惧函数；k为迫使食饵做出反捕食行为的恐惧程度；r0为食饵的内禀增长率；a为食饵种内竞争；c为转化率；g(x)为功能反应函数；di(i=1，2)为自然死亡率。

事实上，除了出生率，食饵的反捕食行为还会影响捕食者的捕获率。此外，现实世界中的随机干扰是处处存在的，种群在环境中不可避免会受到各种随机干扰的影响[17-19]。因此，与确定性模型相比，随机模型更具有真实性。受到文献[20-21]的启发，本文在模型(2)的基础上对随机模型

(3)

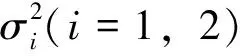
1 预备知识

随机微分方程

dx(t)=f(x(t)，t)dt+g(x(t)，t)dB(t)

(4)

的解记作x(t)=(x1(t)，x2(t)，…，xn(t))(t≥0)。其中：f∈L1(Rn×R+，Rn)；g∈L2(Rn×R+，Rn×m)；B(t)是n维布朗运动。

定理1[22](存在唯一性定理) 假设f(x(t)，t)和g(x(t)，t)关于x(t)满足下列条件：1)局部Lipschitz条件，存在ck>0(k=1，2，…)，使得∀x，y∈Rn且|x|∨|y|≤k，有|f(x，t)-f(y，t)|∨|g(x，t)-g(y，t)|≤ck|x-y|；2)线性增长条件，存在c>0，使得|f(x，t)|∨|g(x，t)|≤c|1+|x||，∀(x，t)∈Rn×R+，则初始条件为x(0)=x0∈Rn的系统(4)存在唯一连续的局部解x(t)(t∈[0，τe))，τe是爆破时间。

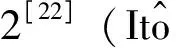
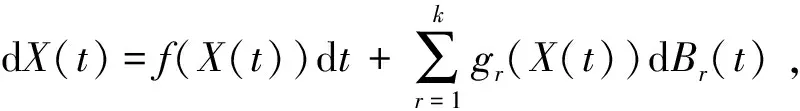
引理1[23-24]对Markov过程X(t)，若具有正则边界的有界区域U∈Rd有如下性质：1)对任意的x∈U，扩散矩阵A(X)的最小特征值是非零的；2)存在非负C2-函数V，使得LV在RdU上为负数，则Markov过程X(t)存在唯一的遍历平稳分布μ(·)。

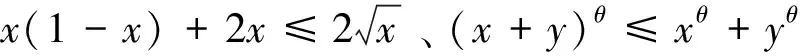
2 全局正解的存在性

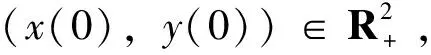
证明首先考虑方程

(5)

令k0>0足够大，使得(x(t)，y(t))∈[1/k0，k0]×[1/k0，k0]，对于任意的正数k≥k0，定义一个停时序列：τk=inf{t∈[0，τe)：x(t)(1/k，k)或y(t)(1/k，k)}。

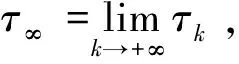
假设τ∞→/∞，则存在常数T1≥0、∈(0，1)和一个正整数k1≥k0，使得P{τk≤T1}≥ε，∀k≥k1。

dV(x，y)=LV(x，y)dt+(x-1)σ1dB1+(y-1)σ2dB2，

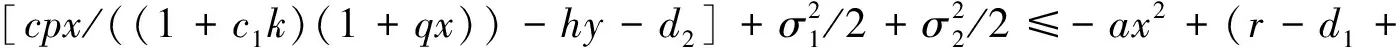
后续证明与文献[26]类似，在此省略。

3 随机持久与灭绝

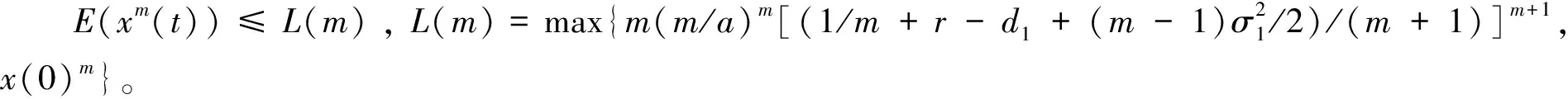
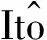
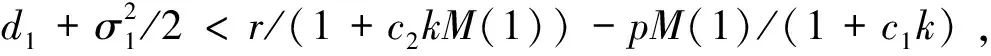
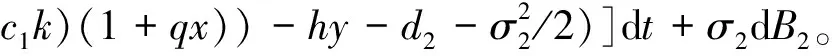
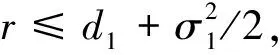
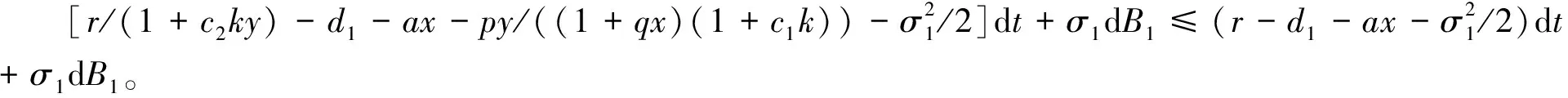
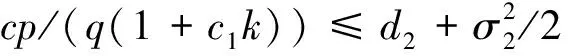
4 遍历平稳分布的存在性

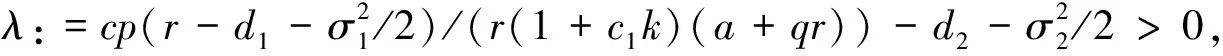
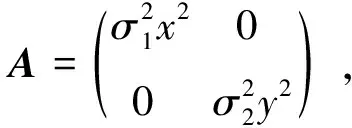
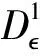
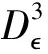
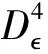
5 数值模拟结果

为了验证上述理论，本文采用Milstein高阶方法[27]对给定初始值和参数的随机模型(3)进行数值模拟。

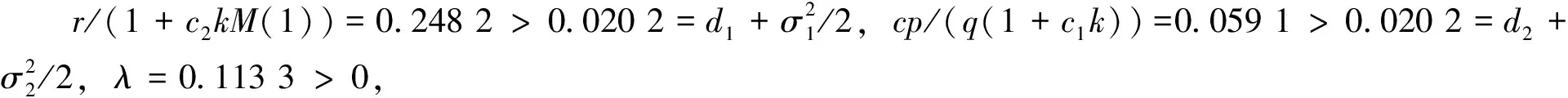
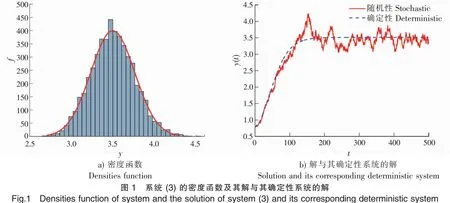
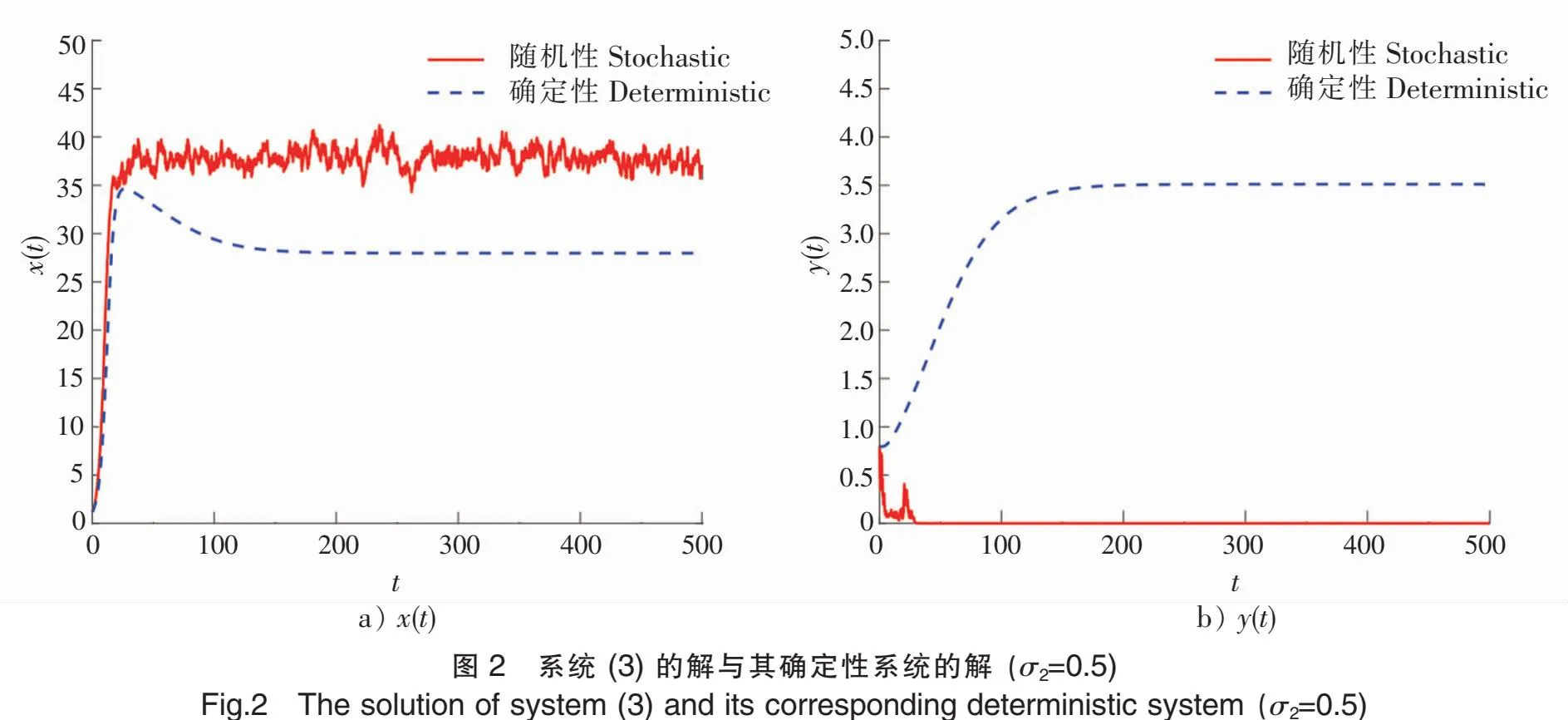
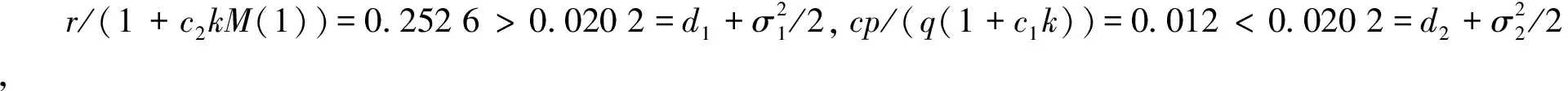
下面讨论白噪声强度σ1和恐惧导致的出生率变化强度c2对系统的影响。

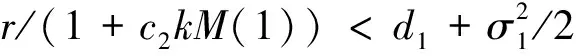
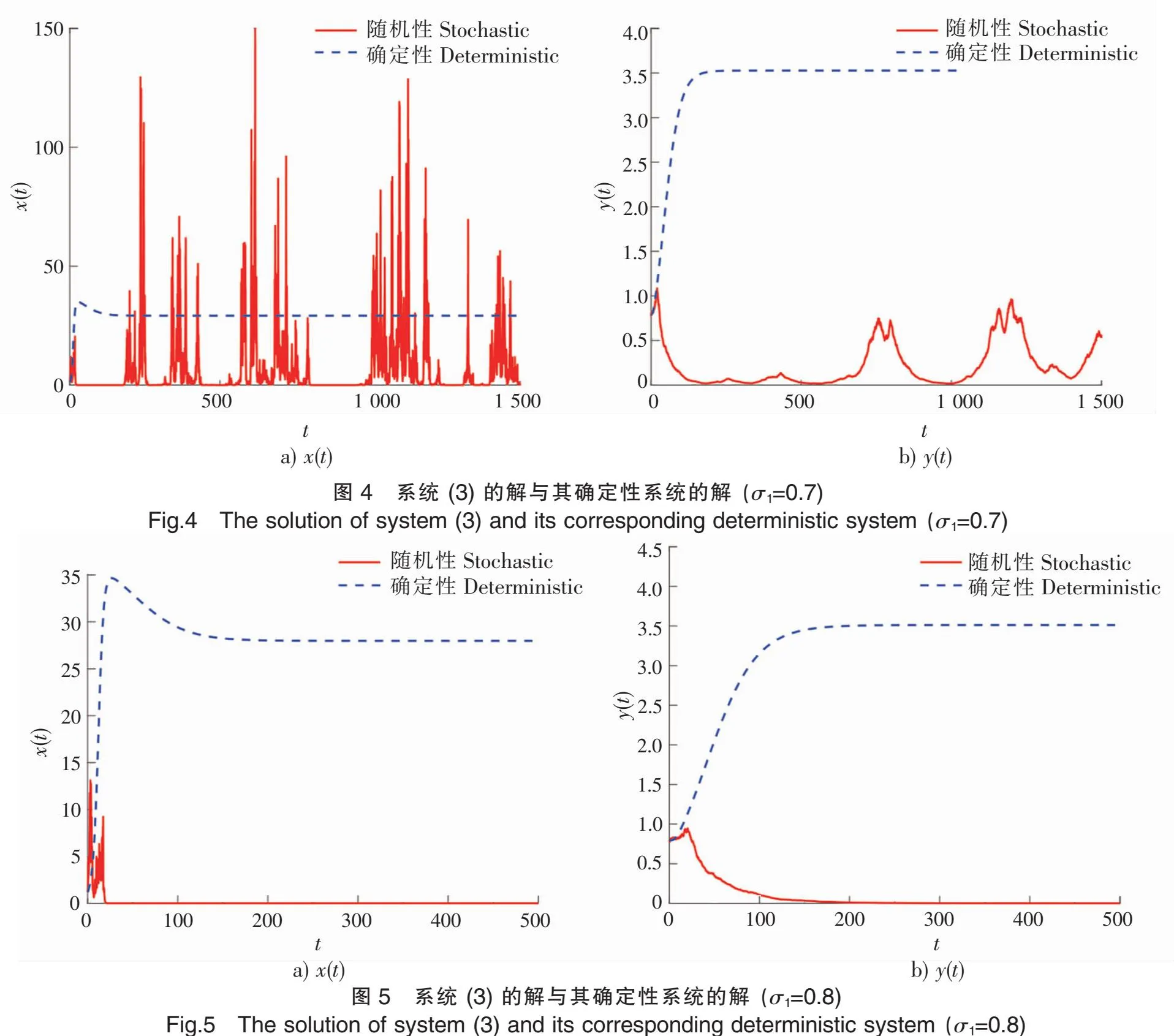
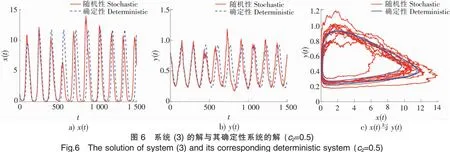
6 结论

本文研究了具有恐惧效应的随机捕食-食饵模型，证明了对于任意给定的正初始值，系统(3)存在唯一的全局正解；得到了系统(3)的平均持续生存与灭绝的充分条件；应用Has’minskii的平稳分布理论，得到了系统(3)存在唯一遍历平稳分布的充分条件。此外，数值模拟结果表明，恐惧效应的存在极大地丰富了捕食食饵模型的动力学。出于对被捕食的恐惧，食饵会表现出一系列反捕食行为，这有利于食饵的生存，并有可能导致捕食者最终灭绝。然而，反捕食行为尤其是更换栖息地对食饵出生率有较大的影响，这不利于食饵新生代的繁殖，并将最终影响整个种群的生存，因此，在捕食食饵模型中考虑恐惧效应是有实际意义的。