运算律的本质、内容进阶与教学建议

刘加霞

【摘   要】五大运算律是代数学的基石，也是小学数学的基本内容。基于加法与乘法的归纳定义可以证明运算律。小学阶段运算律有四个不同的学习阶段，其中第二阶段即四则运算的“用而不述”阶段最为复杂。教师要从更高站位了解运算律的价值，引导学生从代数结构或建构模型的角度“正式”学习运算律，而不必非从“解决实际问题”入手。

【关键词】加法与乘法的本质；运算律；学习进阶

运算的意义、定律和法则是小学数学运算教学的基本内容。在算术中，运算的意义是基础。基于意义可进一步得到运算律，根据意义与定律即可归纳出各种运算法则。在代数中，运算律更为重要。项武义教授指出：简朴得几乎是笨拙的运算律就是整个代数学的基础。［1］3

运算律中具有根基性的就是加法、乘法的规律（数系扩充后，减法就是加法，除法就是乘法），即加法和乘法的交换律、加法和乘法的结合律、乘法对加法的分配律。这五大运算律在小学数学中无处不在。现行多个版本教材都将运算律内容编排在四年级，即运算律在之前所学内容中“隐而不明”，直到四年级才“正式”学习。但基本运算律是与加法和乘法运算同在的［2］，不是到四年级才学习的，即运算律在小学数学中有不同的学习进阶。那么，运算律在小学数学中的学习进阶是什么？不同进阶的内容要求学生理解到什么程度？教师该如何整体把握运算律内容的本质？经历探究、归纳和概括运算律的过程能培育学生哪些核心素养？看似“不证自明”又很容易的运算律真的易于学生理解并掌握吗？这些问题都有待于深入思考，并需要在教学实践中不断探究。

一、运算律的本质与证明

小学阶段所涉及的这五大运算律在数系从自然数系扩充到复数系后仍然成立，根源是其在自然数系中成立。因此，要探究运算律普遍成立的缘由，就得仔细考察自然数系的运算律为什么普遍成立。小学阶段通过举例的方式验证（采用不完全归纳法）并明确性质，但在数学上，举例无法说明定律普遍成立，因为极有可能在无数个例子之外还存在不成立的例子。追根究底地问自然数系的运算律为什么普遍成立，此事绝非庸人自扰，而是学习代数不可缺的奠基与起步［1］4，其中蕴含证明的基本方法——数学归纳法。

数学上的证明，就是以某些事物的正确性去说明其他事物的正确性。任何证明都必须要有依据，不可能“无中生有”。自然数系是一个按顺序排列的体系，起始者为1（皮亚诺修订后的公理规定起始者为0，所以0既是自然数，也是起始者），往后始终按照“后者”比“前者”多1的顺序逐个加1，以至无穷。因此，加法是“+1”的复合。例如，“+n”就是连续n次“+1”的缩写，“+（n+1）”就是“+n”之后再一次“+1”，用算式表示就是a+（n+1）=（a+n）+1。这就是自然数系加法运算的归纳定义，即加法是“+1”的复合。而乘法是自相加的缩写，即1·a=a，2·a=a+a，3·a=2·a+a=a+a+a，也就是（n+1）·a=n·a+a。

在自然数系及加法、乘法定义的基础上，运用数学归纳法就能严格地证明自然数系下的五大运算律。以分配律为例，它的证明过程如下。

要证明m·a+n·a=（m+n）·a成立，须对n作归纳论证。

当n=1时，要证明的等式就是前述乘法的定义。

假设n=k时，m·a +k·a=（m+k）·a成立。

当n=k+1时，

m·a +（k+1）·a=m·a+（k·a+a）      （乘法定义）

=（m·a+ k·a）+a     （加法结合律）

=（m+k）·a+a               （归纳假设）

=［（m+k）+1］·a                （乘法定义）

=［m+（k+1）］·a                    （加法结合律）

虽然在小学阶段不可能要求如上所述的严格的归纳证明，但通过归纳证明的过程可以看出，分配律成立的起点与逻辑基础是乘法的意义及加法结合律。

同样，减法与除法的性质可以通过前述运算律推导出来，所以减法与除法叫“性质”而不叫“运算律”。例如，减法的性质可以这样推导。

a-b-c =a+（-b）+（-c）

=a+（-1）·b+（-1）·c

=a+［（-1）·b+（-1）·c］     （加法结合律）

=a+（-1）·（b+c）         （乘法分配律）

=a-（b+c）

由此可以看出，减法与除法的性质是“流”，加法与乘法的五大运算律是“源”。更进一步说，自然数的加法是根本，是“+1”的复合，乘法是“自身相加”，而减法、除法则分别是加法、乘法的逆运算。当然，在小学阶段，“源”与“流”都承载着各自的育人价值，但“源”更重要。

二、小学阶段运算律的内容进阶以及学生理解的难点

如前所述，运算律虽然简单、朴素，但意义重大。尤其是在代数学中，只要学习四则运算，或利用运算知识解决实际问题，就要涉及运算律，运算律贯穿教学始终，只不过一开始运算律是内隐的，没有外显地、形式化地表述出来。那么，运算律在小学数学中的进阶表现如何？学生如何从模型角度理解运算律、感悟运算律的价值呢？哪些情况下学生易出错？出错的根本原因是什么？为此需要整体分析运算律在小學阶段的内容进阶和“升阶点”。

下面通过对运算律本质和不同版本教材的分析，从运算律的内容、表达方式以及运用情境等方面，按照情境中感知、说理中感悟、字母符号表达及解释运用这几个水平层次，整体划分运算律在小学数学中的学习阶段。

【阶段1】直观感知：具体情境中感知交换律

加法、乘法交换律在学生一、二年级学习加法、乘法意义时就可以揭示，让学生结合具体情境，通过列式知道3+5=5+3、3×5=5×3这样的基本事实，但不需要用抽象的字母符号来表示。加法交换律、结合律的情境基于生活经验，学生容易感知。甚至从并集的角度看，加法交换律自然成立。如俄罗斯一年级教材在加法定义之后，就立刻根据并集的意义写出了“T+K=K+T”，加法交换律出现得很早。［3］

对于选择哪个合适的情境认识乘法交换律，目前学界观点不同，仍有争议。例如，在“初步认识乘法”中，如果采用“每个盘子装3个苹果，5个盘子一共装多少苹果”这一情境，所列算式“3+3+3+3+3”只能改写为“3×5”，而不能直接写“5×3”。只有在借助“点阵模型”求一共有多少个点时，学生才能更好地理解乘法交换律，因为这时可以从两个角度研究点的个数：每行有3个，有这样的5行（5个3相加）；每列有5个，有这样的3列（3个5相加）。观察与计算的角度不同，所列算式也不同，但结果都一样，所以3×5=5×3，即交换乘数的位置，乘积不变。虽然现行教材不再区分被乘数、乘数，但在某些情境下二者含义不同，只有在点阵模型中二者的地位才对等。二年级学生应该能够理解“两个数相乘，交换它们的次序乘积不变”的结论，不过仅限于具体数相乘。至于出现a×b=b×a那样的字母表达式，以及采用乘法交换律这样的专有名词，仍旧可到四年级再提出。［4］

【阶段2】计算中“用而不述”：说理中感悟结合律与分配律

四则运算能够“算下去”，都是在运用基本运算律。运算律是计算算理的主要依据之一，在本阶段中还可以再细分为以下几个“小阶段”。

（1）自然数和小数都是十进制数，其加减法的算理完全相同，计算过程中多次运用加法的交换律、结合律。

（2）分数加减法的算理，本质仍然是“相同计数单位的个数相加减”。由于需要借助通分找到更小的相同分数单位，其难度要比自然数、小数更大，但比自然数乘法的难度小一些。

（3）多位数乘一位数与除数是一位数的除法都需要较简单地运用乘法分配律，处于同一层级，学生理解起来不难。其中除法也不难，如用竖式计算26÷2，就是将26拆分为（20+6），然后再分别除以2，其本质还是乘法分配律。除数是两位数时，算理仍然运用乘法分配律。虽然由于除数较大，具体计算时要调商、试商，计算难度增加，但算理一样。

（4）多位数乘两位数则需要两次运用分配律，且涉及多个数相加的分配律，而不只是两个数相加，所以该内容比前面三个阶段的算理更难。

例如：234×35=234×（5+30）

=234×5+234×30

=（200+30+4）×5+（200+30+4）×30

（5）分数、小数的乘除法处于同一层级。其中，分数乘除法的本质是“计数单位的个数乘个数、计数单位乘计数单位”，在此过程中多次运用交换律与结合律。一般来说，应该先学习分数乘除法，后学习小数乘除法，将小数转化为分数来计算并说理。这样设计课程内容将降低小数乘除法的难度，但现行各版本教材都不是这样编排的。

运算律在上述各层级中都是“隐身”的，因此，在教学中应该让学生通过列横式感悟运算律。正如史宁中教授所说的：横式比竖式重要。计算教学中，多让学生用横式表达计算过程非常重要，这能为他们正式地学习运算律、构建各运算律的模型积累基本的活动经验。

【阶段3】理性符号化：整体把握用字母符号表示的五大运算律

本阶段内容各个版本教材都会编排，但不同教材的编写方式不同。现行多数版本教材都以“运算”为主线，先学习加法的交换律、结合律，再学习乘法的交换律、结合律，最后学习乘法对加法的分配律。但北师大版教材以“运算律”为主线，先学习加法、乘法的交换律，再学习加法、乘法的结合律，最后学习分配律。不同版本教材的编排方式各有优点和不足，教学的关键是探究发现运算律的方式是什么。北师大版教材的编写在这方面有很好的体现，后文将具体介绍。

【阶段4】解释迁移：应用运算律灵活解决简单问题

小学阶段要求学生简单地运用运算律进行简便计算。然而，有意识地、自主地进行简便计算对小学生而言很难。其原因较为复杂，既有学习态度方面的问题，也有知识掌握不牢固、错误运用运算律等因素，但最主要的因素还是学生的算术思维在“作祟”，因而不能从“结构”的角度整体研究算式的特征。

真正理解运算律需要学生具备一定的代数思维，或者说学习运算律是培养学生代数思维的重要载体。五大运算律中，加法与乘法的交换律只涉及两个运算对象，学生容易掌握，但需要让学生认识到“交换位置”进行运算不是在所有情况下都适用的，如在减法和除法中就不成立。而学生最易混淆的是加法、乘法的结合律及乘法对加法的分配律。它们都涉及三个运算对象、两次运算，尤其是分配律中还要进行两次不同的运算。虽然五大运算律是显而易见的事实，单独认识某一个都较为容易，但运用运算律解决实际问题时却极易出错。表面上看是学生容易混淆不同运算律，实际上却是学生的算术思维在“作祟”：总想算出某个算式的具体数值，而不能有效运用运算律，从整体结构的角度观察算式，因为这需要学生具有一定的代数思维水平。

例如，计算87+38+23时，大多数学生习惯性地按照运算顺序逐步计算，而不会“主动地”先观察算式中每个数的特点，然后正确运用定律进行简便计算。在算术运算中，按照运算法则“先算小括号里面的，再算中括号里面的；先算乘除法，再算加减法”总能计算出结果，这样程序性的计算并不能体现运算律的价值。而代数运算不同，没有运算律可以说“寸步难行”。如计算代数式9+2（x-3）时，因为括号里算不出具体的数，所以必须运用分配律“去掉括号”得到2x+3，这是算术运算与代数运算的真正分野。由算术运算进步到代数运算的关键在于数系运算律（特别是分配律）的系统运用，即以通性求通解。在算术运算中基本不用分配律，乃是数学的石器时代；及至代数运算，则系统地运用分配律去简化各种各样的代数式和代数关系，这就进步到数学的铜器时代了。［1］12五大运算律中最有力量的是分配律，它也是学生最难理解和运用的，在后文教学建议部分将进一步分析如何引導学生从模式建构角度学习分配律。

三、运算律单元教学的几点建议

关于运算律单元的教学，笔者从学习进阶、模型建构及对教师专业知识的期望角度提出以下建议。

（一）“正式”学习运算律时不要从“解决现实问题”导入

如前所述，如果教师在学生处于阶段1、阶段2时就“捅破”加法、乘法具有交换律、结合律，在学生正式认识运算律时就不需要再从解决现实问题入手。如果教师从解决问题入手，学生必然列一个算式就能计算出得数，至此已能解决问题。此时教师再引导学生通过观察两个结果相等的不同算式，得到两个算式相等的活动，学生已不再有学习的需求与愿望。北师大版教材关于如何学习运算律的编排方式值得借鉴，主要包括以下几步。

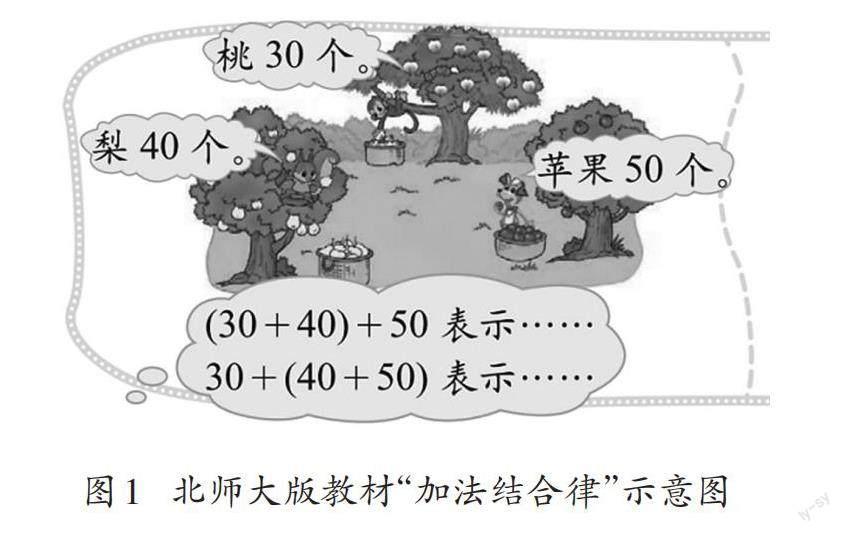
第一步，直接从观察一组纯数学算式入手，寻找算式之间的等量关系，建立等式，并用语言描述其特点，初步感悟运算律（如图1）。第二步，举生活事例解释等式左右两边算式的意义，紧扣运算的意义而不强调计算的结果。如果是解决实际问题，必然要强调计算结果。但从计算结果相等的角度认识等式，没有必要写出等式，且培养的只是学生的算术思维。而紧扣算式的意义也就是加法、乘法的意义，从而判断两个算式之间能不能写“=”却是典型的代数思维。第三、第四步，用字母表达式表示运算律，并运用运算律进行简便计算。

让学生经历归纳算式感悟特征、用生活事例（现实模型）解释等式意义及理解运算律的本质、符号表示达到形式化理解等过程，既不脱离运算律的数学本质，又有助于学生的学习进阶。这样的学习不仅符合学生的学习兴趣，而且能潜移默化地培养学生的模型意识与代数思维，使知识目标与能力、素养目标有机融为一体。

（二）几何直观模型贯穿运算律单元教学的始终

几何直观模型是理解代数知识的重要抓手，它能将抽象的代数内容可视化。对小学生而言，借助几何直观模型理解运算律更为重要。几何直观模型要贯穿运算律单元的始终，具体内容如下。

加法交换律、结合律：线段图。

乘法交换律：矩形模型，可以是点阵图、方格图，还可以抽象为长方形面积图。

乘法结合律：长方体模型，由“小正方体”堆积而成的长方体。

乘法分配律：组合的矩形模型。

下面简要说明如何用组合的矩形模型来学习乘法分配律（图省略）。

首先，用若干个有相同“长”或“宽”的长方形，拼摆成更大的长方形，并用算式表示拼前、拼后各长方形的面积，感悟能够“拼成”的秘密——共用的边（算式中就是“公因子”）。

其次，以4×9的长方形为“基础图形”，再补一个长方形使之成为更大的长方形，仍用算式表示面积关系。学生有的按照“长”不变、有的按照“宽”不变来补新的长方形。汇报时，先交流“长”不变的情况，引导学生感悟面积之间的关系式为9×（4+c）=9×4+9×c。

最后，在前面“补图形”的基础上，通过课件演示，让学生明白“4”“9”都可以变，所以面积之间的关系式为a×（b+c）=a×b+a×c，这就是乘法分配律。

（三）教师应该从更高站位认识运算律的价值

运算律不仅能帮助人们进行简便计算，它在数集扩充中也扮演了非常重要的角色。例如：为了满足减法运算的封闭性（即两个相同集合中的对象作运算，其结果仍属于该集合），产生负数，即在自然数集基础上扩充为整数集；为了满足除法运算的封闭性，产生分数，自然数集扩充为有理数集。在扩充后的新的数集（有理数集、实数集、复数集）中，自然数的运算律必须依然保持有效。运算律的重要性同样体现在代数学中，整个代数学所发展的就是如何有系统、有效力地运用这一系列简朴的、普遍成立的数系运算律去解决各种各样的代数问题。基本运算律以及初中阶段要学习的指数运算法则，被统称为“数与代数”领域的“通性通法”，而被称为通性通法的数学内容都是最根本、最重要的。

对于这些内容，只要求小学教师有较高站位的了解，感兴趣的教师可以查阅相关资料进一步学习，适当时机可以跟对此感兴趣的学生一起来研究，因为关注这样的“基本问题”是培養拔尖创新人才的根本。因此，即使在小学也要让学生感悟到学数学不只是为了解决身边“买东西、旅游、运货”等现实问题，更是为了发展自身的思维能力。

参考文献：

［1］项武义.基础代数学［M］.北京：人民教育出版社，2004.

［2］王永.漫谈运算与基本运算律［J］.福建论坛（社科教育版），2005（11）：36-37.

［3］巩子坤，张奠宙，任敏龙，等.教学运算律，须先厘清运算的本质［J］.小学数学教师，2017（7/8）：15-18.

［4］张奠宙，戎松魁.正本清源，通过“数数”活动理解运算律：关于加法和乘法交换律的讨论［J］.教学月刊·小学版（数学），2015（6）：4-6.

（北京教育学院数学与科学教育学院）