“算法”的双刃性与“算理”的局限性
【摘 要】《义务教育数学课程标准(2022年版)》重视算法和算理的关系,将计算过程的不同表征方式之间的关系视为算法和算理的关系,表现为“用符号解释符号”,容易导致教学中对计算程序及其逻辑基础的强化,使计算过程成为无理解的机械操作。这样的算法和算理在数学课程内容与实际教学中分别具有利弊并举的双刃性和意义缺失的局限性,教学效果表现为“虽然会算但不知为什么算,虽然算对但不知算的是什么”。因此需要进一步拓展算理的含义,进而走向“寓理于算”的数学教学。
【关键词】算法;算理;计算;计算之理
《义务教育数学课程标准(2022年版)》(以下简称“2022年版课标”)中,“算法”和“算理”两个词相伴出现12次,反复强调“经历算理和算法的探索过程”及“理解算理与算法之间的关系”,可见2022年版课标制订者对算理与算法之间关系的重视。对于依据2022年版课标进行的教科书编修以及实际教学,应当注意到2022年版课标中所说的“算法”和“算理”分别具有利弊并举的双刃性和意义缺失的局限性。
一、2022年版课标中的算法与算理
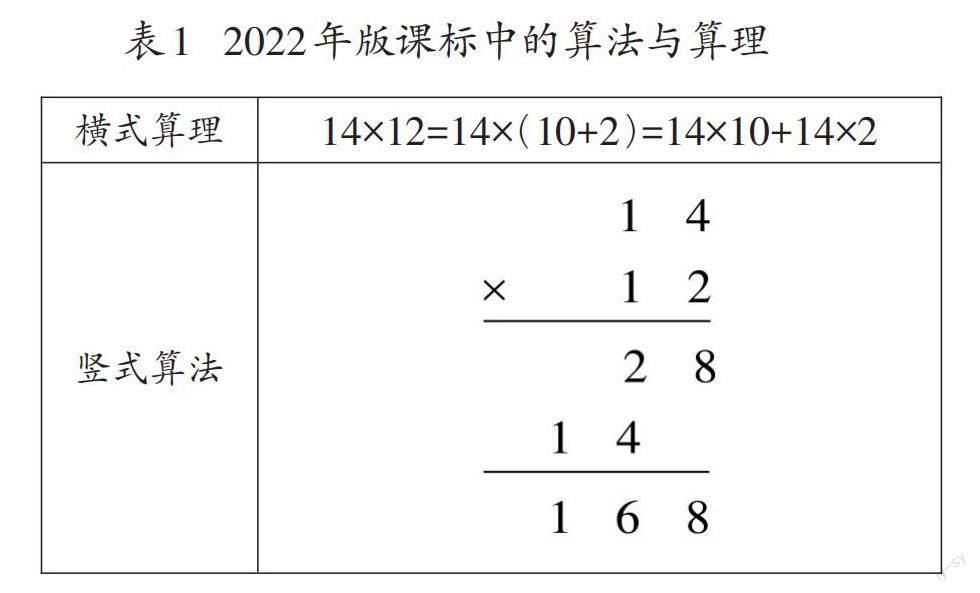
通览2022年版课标,并未发现对“算法”与“算理”含义的明确解释,因此只能在语境中进行猜测或推断。2022年版课标在第103页例8对两位数乘法14×12的说明中同时出现了算法和算理:“可以引导学生将12分解成(10+2),然后利用横式体现算理,14×12=14×(10+2)=14×10+14×2,就可以把未知转化为已知;在分析的基础上建立乘法运算竖式,从算理过渡到算法。”从这段文字表述看,对于两位数乘两位数14×12的计算,2022年版课标修订者把计算过程写为竖式叫作算法,同时写为横式视为体现竖式的算理(如表1)。
这样区分算法与算理令人费解。无论是写为横式还是竖式,都是依据十进制记数的位值原理以及乘法分配律对计算过程进行的符号表征。虽然从形式上看,横向与纵向的书写方式不同,相对于竖式,横式是将“12”分为“10+2”,从视觉上将十进制记数法的位值可视化,但从思维的角度看,横式与竖式并无明显差异。因此,横式和竖式至多可以认为是同一计算过程的两种符号记法或写法。
这种似是而非的解释容易误导教科书的编修及一线教师的教学。根据对北京一些小学课堂教学的观察,教师强制学生必须同时写出横式与竖式的现象普遍存在,理由是用竖式表达计算过程时,写出横式就体现了算法与算理的关系,是遵照2022年版课标要求的做法。这样的教学强化了演绎推理过程中前提条件和推理过程逻辑意义的确定性[1],弱化了计算过程中的合情推理,会对发展学生“差异的眼光、灵活的思维、丰富的语言”产生消极、负面的影响。因此,2022年版课标中所说的算法和算理对于素养导向的数学课程与教学而言具有利弊并举的双刃性和意义缺失的局限性。
二、算法的利与弊
“算法”的词义有广义与狭义之分。我国历史上作为学科的数学也叫“算学”,解决数学问题的方法都可以叫作“算法”[2]。比如,《孙子算经》中的“鸡兔同笼”问题:“今有雉兔同笼,上有三十五頭,下有九十四足。问雉兔各几何?”用现在的语言叙述即:“笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。问鸡和兔各有多少只?”《孙子算经》中所表述的半足术就表现为解决问题的算法:“半其足,以头除足,以足除头即得。”[3]这一算法的解题过程分为如下三个步骤。
第一步(半其足):取总足数94的一半,得到47。
第二步(以头除足):这里的“除”是“减”的意思,用47减去总头数35,得到兔的只数为12。
第三步(以足除头):用35减去12,得到鸡的只数为23。
诸如此类的算法,凸显的是解题过程的程序执行与步骤操作,其中的“算”,既可以是数值计算,也可以是解决问题过程中的执行与操作,因此是广义的算法。2022年版课标中所说的算法窄化了算法的本义,特指笔算(数值计算)过程的标准记法或写法。小学数学课程中,用数字符号记录计算过程的竖式就是典型的标准写法,不妨称为狭义的算法。无论是广义还是狭义的算法,都具有共同的属性,具体可以概括为:
l过程的程序性
l结果的可靠性
l应用的广泛性
l思维的简约性[4]
任何算法都表现为过程的程序性,都是由依据想法或规则而设置的步骤构成,且步骤之间的关系具有先后顺序的确定性。程序的执行与操作需要遵循的准则可以概括为:
l按部就班
l依次执行
l操作无误
以14×12的计算为例,为了获得准确无误的计算结果,依据十进制记数法及乘法分配律,将计算过程设置为如下步骤。
第一步:将12分为10+2。
第二步:用14与10和2分别相乘。
第三步:将14与10及14与2相乘的结果相加。
第四步:得到计算结果168。
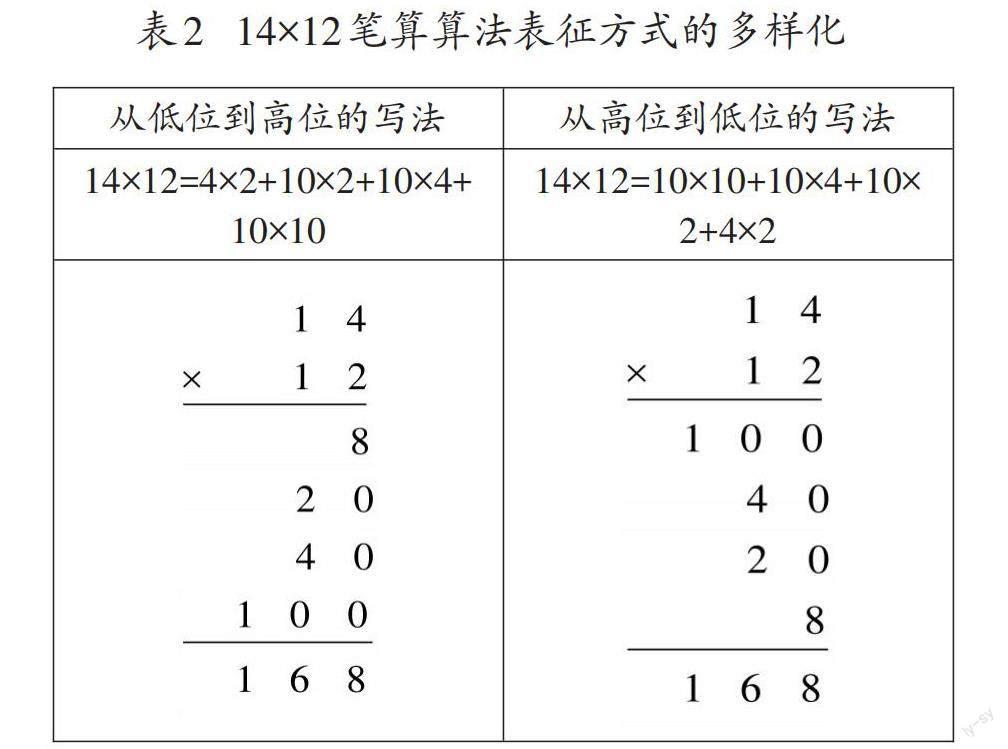
前文中,表1内的横式与竖式都是记录这一程序的写法。这样的写法还可以进一步细化,比如把14也改写为10+4,由此可以产生更多的写法,既可以从低位写到高位,也可以从高位写到低位(如表2)。
针对14×12的计算,表1和表2的不同写法并无本质差异,都是依据十进制记数法和乘法分配律所设计的程序进行的符号表征,因此应当视为笔算算法表征方式的多样化[5],是数学语言丰富性的体现,并非算理与算法的关系。
算法的程序性使得依据算法计算的结果具有唯一确定的“可靠性(Reliability)”,只要遵循算法的程序按部就班、依次执行、操作无误,就可以确保计算结果的准确。作为计算方法的算法同时还具有应用的“广泛性(Generality)”,即在某范围内普遍适用,比如两位数乘两位数的竖式算法同样适用于其他整数与小数的乘法计算。
算法的程序性、可靠性与广泛性使得算法的执行与操作具有了“可信”和“易行”的特征。“可信”指的是只要执行过程中操作无误,则结果必定准确;“易行”则表现为执行与操作过程中思维活动的简约,亦步亦趋地“模仿、记忆、练习”就可以实现“又对又快”。“可信”与“易行”的特征使得算法成为能够用简约的思维活动达成目标的工具,契合了奥地利-捷克物理学家、心理学家、哲学家恩斯特·马赫(Ernst Mach,1838—1916)所说的“思维经济原则(Economic Principle)”[6]。
如果把计算教学的目标定位于“又对又快”,即计算结果的准确与计算过程的快捷,那么将计算教学“算法化(Algorithmization)”就成为自然的选择。由此形成算法化的教学套路“讲解—示范—留作业”,相应的学习过程就变成“倾听—模仿—做练习”的模式。“亦步亦趋地模仿”可以确保准确无误,“大量重复的练习”可以实现操作熟练,因此算法化的教学对于实现“又对又快”的教学目标自然是有效的。
长期以来,数学课程与教学中的算法化倾向饱受争议,原因在于算法本身具有利弊并举的双刃性。一方面是可信与易行,另一方面也呈现出常规性“套路(Routine)”的特征[7],对执行与操作者或学习者有“排斥思维(Driving out Thought)”的效应[8]。从教育的视角看计算教学,过度强化算法自然会弱化对算法发生与设计的原创以及对算法意义的理解,使得计算过程成为“无理解的机械操作”[9]。
因此,对算法的教学需要兴利除弊,既要求熟练掌握算法,也要求对算法的原创、设计与理解,这或许是2022年版课标修订者重视算理与算法关系的初心,意在表达用算理理解算法的重要性。那么算理又是什么意思呢?
三、广义的“算理”
“算理”一词是汉语的原创,含义相当广泛,很难找到确定、恰当的英文单词与之对应,其含义的广泛性使之具有极强的语境依赖性[10]。其中的“算”既可以是广义的算学(数学),也可以是相对狭义的运算(计算);“理”表达的含义则更为抽象、广泛,在中国历史文化中与形而上的“道”同义[11]。因此需要在不同语境中提取并提炼算理的含义。
19~20世纪英国哲学家、数学家、逻辑学家、历史学家、文学家伯特兰·阿瑟·威廉·罗素(Bertrand Arthur William Russell,1872—1970),将数学学科的发展分为两个相对的方向。第一个方向是“建构的(Constructive)”拓展,如数的系统从自然数的范围逐步扩大到整数、有理数、实数、复数,在此基础上进一步抽象出集合与函数等数学对象,自然数中的运算也随之应用到诸如此类新的对象中。这样的建构使得数学的学科内容逐步拓展,应用的领域逐渐扩大。
第二个方向与建构的拓展相反,是为数学的发展寻找起点,为数学理论体系建立“逻辑基础(Logical Foundation)”。罗素分别用“望远镜”和“显微镜”隐喻这两个方向的研究,望远镜让人看得更高、更远、更广阔,而显微镜能够看得更细、更准、更精确[12]。
为了开展数学逻辑基础显微镜式的研究,罗素于1919年出版了题为An Introduction to Mathematical Philosophy的著作。我国20世纪数学家傅种孙等人在翻译此书时,将书名译为《罗素算理哲学》[13]。其中“mathematical”在英汉词典中的意思通常为“数学的”,傅种孙等人将其译为“算理”,原因应当是认为本书主题与通常所说的数学不同,指向的是数学学科的逻辑基础,由此推断傅种孙等人认为的“算理”实质是数学之理[14]。我国20世纪著名逻辑学家晏成书译著的另一个中译本,将书名译为《数理哲学导论》[15],其中的“数理”与傅种孙等人翻译的“算理”同义,进一步证实了算理具有“数学之理”的含义。
《罗素算理哲学》中的“哲学(Philosophy)”一词,可以理解为如何看待数学的思想观念,这样的思想观念具有主观差异性,不同数学家对数学之理的看法也是千差万别的。如19~20世纪著名物理学家、数学家胡明复称“算理即事理”[16],数学作为抽象的学科,其发生、发展的动因、规律等思想观念都可以归属于算理的范畴,凡此算理虽然源于人的心智,但与“事理”是相通的,即数学与现实世界中的事物、事件及其发展规律密切相关。
综上所述,广义的算理一方面可以视为如何看待数学的思想观念,另一方面也是数学学科理论的逻辑基础。这样的算理远比2022年版课标中所说的算理的含义更广泛。从前文的分析看,2022年版课标中的算理应当归属于算术中的计算,可以叫作“计算之理”。
四、“计算之理”的不足
“计算”一词的本义是以算筹(小棒)为工具的计数活动[17],与源于古拉丁语“calculus”的英文单词“calculation”(本义是人用石子计数的过程[18])基本同义。如今所说的“计算”是把作为实物的小棒或石子改变为数字或字母符号,由此,数学课程中的“计算”就成为针对符号所构成的算式,应用相应的算法,通过执行与操作,从而获得结果的过程。比如前文中的14×12就是数字符号所构成的算式,针对这一算式,应用相应的算法,獲得结果为168的过程,就是“计算14×12”的过程。
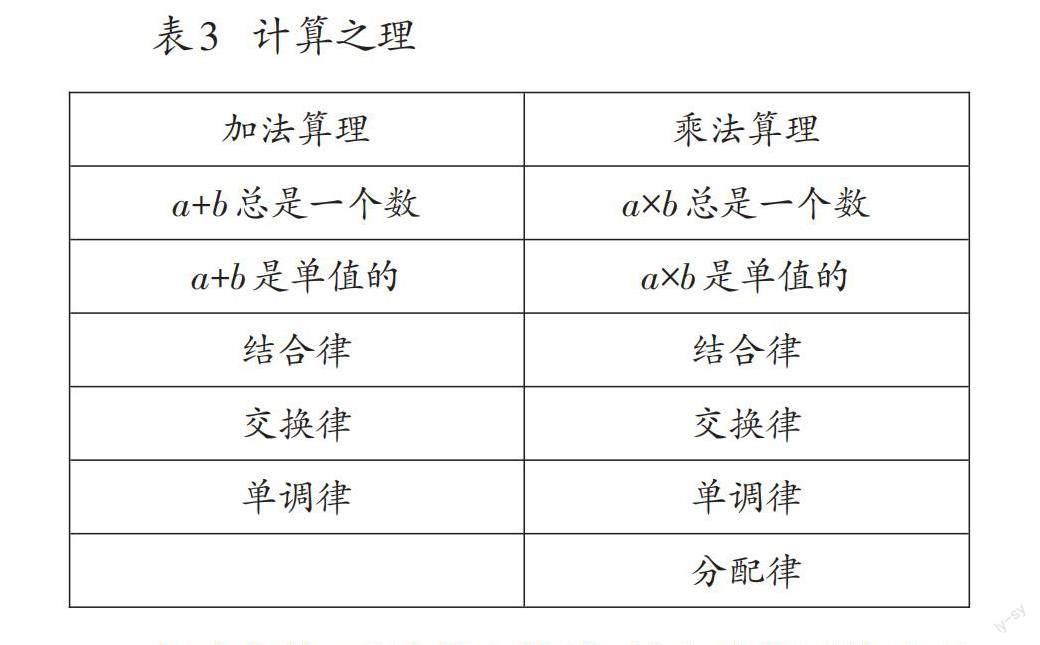
任何计算过程都表现为对算法的设计、执行与操作。算法的设计具有因人而异的主观性,不同的人可能设计出不同的算法,由此就会带来可靠性的风险。按照德国数学家、数学教育家菲利克斯·克莱因(Felix Klein,1849—1925)在《高观点下的初等数学》一书中所说:需要规定性的“规则(Laws)管控(Governing)”计算的算法[19]。只要遵守规则,则确保计算结果的准确无误。这样的规则就成为计算的逻辑基础,即“计算之理”。克莱因在众家之说的基础上,将算术基本运算中加法和乘法的计算之理归纳为11条(如表3)。
其中加法、乘法的交换律、结合律和乘法分配律是我国小学数学课程中为人熟知的运算律,人们相对陌生的前两条“总是一个数”和“单值的”,分别指的是运算结果的存在性和唯一性,第五条的“单调律”指的是“如果b>c,那么a+b>a+c或a×b>a×c(a>0)”。
如果把表1和表2中的计算过程视为表达算法的符号语言,那么表3中的计算之理就相当于管控语言时使用的“语法”,是确认计算算法执行与操作过程中“为什么可以这样”的规则。如果问“为什么可以把14×(10+2)写为14×10+14×2”,那么表3中的分配律就成为支配与管控这一写法的规则。因此,计算之理实质是确保计算算法可靠性的逻辑基础,是支配与管控算法执行与操作的规则。
无论是广义的算学之理,还是狭义的计算之理,其中的“理”都指向“为什么可以这样”,进而确保算法的可靠性。用我国宋代著名思想家朱熹的理学观点来说,计算之理是计算过程的“所当然之则”,即“当然如此”的依据[20]。
应当注意的是,“当然”不等于“必然”。如果意图将两位数与两位数的乘法14×12转化为两位数与整十数及一位数的乘法,2022年版课标中的横式写法“14×10+14×2”是一种“当然”,但不是“必然”,并不意味着必须如此。比如依据乘法意义的“比例说”[21],14×12还可以写为:
l14×12=(14×2)×(12÷2)=28×6
l14×12=(14×3)×(12÷3)=42×4
2001年颁布的《全日制义务教育数学课程标准(实验稿)》所倡导的“算法多样化”应当就是这样的意义。遗憾的是,在最新颁布的2022年版课标中,“算法多样化”的说法消失了。教学中,切忌将2022年版课标或教科书中的写法视为唯一正确,而应当树立“目标是确定的,方法是多样的”的观念。
综上所述,2022年版课标中所说的算理实质应当是计算算法的逻辑基础,即通常所说的运算律,是算法执行与操作的依据,是支配、管控算法的规则。其局限性在于算理的表征形式与算法的表征形式同属符号世界,使得算理与算法的关系成为“用符号解释符号”,即符号世界内部的自圆其说,缺失了符号所指代的实际意义。
五、结语:突破算理的局限性
2022年版课标中所说的算法具有利弊并举的双刃性,而算理具有“用符号解释符号”的局限性。因此需要拓展对算理的认识,突破其局限性,使算理不仅指向逻辑上的计算之理,同时指向运算的意义。
我国20世纪著名教育家、数学教学法大师俞子夷先生早在1935年出版的《小学算术教学之研究》一书中就专门论述过“意义的学习”:“文字、数目都是一种符号,要是没有和事物发生关系,就没有什么意义。”[22]将算理与算法的关系局限于“用符号解释符号”,或许可以做到计算的“又对又快”,但难以实现对运算意义的理解,极易导致“虽然会算但不知为什么算,虽然算对但不知算的是什么”的反效教学。
计算之理并非算理含义的全部,算理的课程价值不仅是支配、管控算法的逻辑规则,同时也应当包括运算“何时出现”的思维生成,以及运算过程中“发生了什么”的原因解释。这样的“寓理于算”已经超越了符号世界内部的自圆其说,让符号世界与事物世界建立联系,进而实现有意义的学习,更加全面地彰显出算理的课程与教育价值。
“算理”一词含义的广泛性为重新认识数学课程中的算理提供了可能。因此,为了突破计算之理的局限,就需要进一步探究算理的其他含义,重新界定数学课程与教学中的算理。(篇幅所限,另文续谈)
参考文献:
[1]巩子坤,张希,金晶,等. 程序性知识课程设计的新视角:算理贯通,算法统整[J].课程·教材·教法,2021,41(6):89-95.
[2]李继闵. 算法的源流:东方古典数学的特征[M].北京:科学出版社,2007.
[3]郜舒竹. 鸡兔同笼问题中的辩证思维[J].课程·教材·教法,2019,39(9):88-93.
[4]BASS H. Computational fluency,algorithms,and mathematical proficiency:One mathematicians perspective[J]. Teaching Children Mathematics,2003,9(6):322-327.
[5]郜舒竹. 笔算方法多样性的历史考察[J].课程·教材·教法, 2016,36(1):88-94.
[6]孙小礼. 马赫和他的思维经济原则[J].哲学研究,1986(10):29-36.
[7]STEIBRING H. Routine and meaning in the mathematics classroom[J]. For the Learning of Mathematics,1989,9(2):24-33.
[8]STEIN S K. Greshams law:Algorithm drives out thought[J]. For the Learning of Mathematics,1987,7(2):2-4.
[9]SCANDVRA J M. Algorithm learning and problem solving[J].The Journal of Experimental Education,1966,34(4):1-6.
[10]张帆,刘华文. 理學核心概念“理”的现当代英译述评[J].中国翻译,2022,43(4):120-128,192.
[11]吾淳. “理”概念发展的知识线索[J].上海师范大学学报(哲学社会科学版),2013,42(6):14-23.
[12]RUSSELL B. Introduction to mathematical philosophy[M]. London:George Allen & Unwin Ltd,1919:2.
[13]苏日娜,代钦. 傅种孙译著《罗素算理哲学》及其引起的学术争论[J].数学通报,2014,53(4):41-45,48.
[14]苏日娜,代钦,敖特根.《罗素算理哲学》与数理逻辑在中国的早期传播[J].自然辩证法通讯,2019,41(11):62-66.
[15]罗素.数理哲学导论[M].晏成书,译.北京:商务印书馆,2010.
[16]宋晋凯,张培富. 民国算学哲学反思之先声:胡明复算学思想探析[J].山西大学学报(哲学社会科学版), 2019,42(2):129-133.
[17]杜石然. 数学·历史·社会[M].沈阳:辽宁教育出版社,2003:8.
[18]LEVEY M. Abraham Savasorda and his algorism:A study in early European logistic[J]. Osiris,1954(11):50-64.
[19]克莱因. 高观点下的初等数学(第一卷)[M]. 舒湘芹,陈义章,杨钦樑,译.上海:复旦大学出版社,2008:5-6.
[20]张岱年. 论当然[J].北京大学学报(哲学社会科学版), 1996(5):73-78,127.
[21]郜舒竹. 乘法,真的是加法吗?[J].教学月刊·小学版(数学),2023(9):4-10.
[22]俞子夷. 小学算术教学之研究[M].上海:中华书局,1935:47.
(首都师范大学初等教育学院)

