高阻隔非金属柔性复合管承压性能模拟

张学敏，王庆岗，张雪茹，李厚补，齐国权，丁 晗，高 雄，杨文辉

（1. 长安大学材料科学与工程学院，西安 710064；2. 中国石油集团工程材料研究院有限公司，西安 710077；3. 陕西延长石油西北橡胶有限责任公司，陕西 咸阳 712023）

0 前言

非金属柔性复合管具有耐腐蚀、质量轻、运输和施工方便等优点，是油田地面集输管网的优选管材［1-3］。非金属柔性复合管结构分为内衬层、纤维增强层以及外保护层。纤维增强层使用芳纶纤维丝带、聚乙烯纤维丝带、聚酰胺纤维丝带等编织物采用一定的角度进行多层铺设缠绕而成［4-6］。内衬层和外保护层均为聚合物材料，如交联聚乙烯（PEX）、聚偏氟乙烯（PVDF）、高密度聚乙烯（PE-HD）等热塑性塑料［7-8］。在油气集输过程中，因聚合物的本质特性，直接与介质接触的内衬层易发生气体渗透现象。气体渗透不仅会浪费输送气体，还会使内衬层发生起泡、坍塌等失效，甚至造成复合管承压能力下降及使用寿命缩短［9］。因此，提高管道的抗阻隔能力［10-12］成为非金属管道研发的热点。

齐国权等［13］针对非金属管道的气体渗透行为，研究了气体在增强热塑性塑料管道中渗透行为控制方法，并从自身材料改性、高阻隔性材料引进、化学反应消耗以及集中气体排放等方面进行逐级控制。Hui等［14］采用机械共混法和热压法制备了具有不同界面黏附性能的GO/超高分子量聚乙烯（PE-UHMW）复合材料，其气体阻隔能力相较于PE-UHMW 提升近50 %。Karolina 等［15］利用熔融挤压工艺和预涂覆复合方法获得各向异性低密度聚乙烯（PE-LD）复合材料，通过填充均匀分散的石墨烯纳米片（GnP）来降低PE-LD 复合材料气体渗透能力。Baker Hughes 推出以聚酰胺（PA）和聚苯硫醚（PPS）为内衬层的柔性复合管，PA和PPS 气体阻隔性明显优于PE-HD，适合于高温输气（H2S、CO2等）工况。张红梅［16］研究了带有乙烯/乙烯醇共聚物阻隔层的PE-HD 管道阻隔性能，并进行长达60天的测试，结果表明管道可有效阻隔气液介质发生渗透。宁波欧佩亚海洋工程装备有限公司在内衬管添加了一层具有优良气体阻隔性能的EVOH 材料，其耐氢气和甲烷的渗透性能比PE-HD 和PA6要优越很多，但价格昂贵，故未大量使用。除选用或添加阻隔性好的材料外，还可通过在管体结构中引入阻隔层来提高管体的阻隔性，如法国IFP 新能源公司［17］研发了一种“抗硫管道”，其基体采用PE 材料，内压密封层和环空之间增设了一层H2S 吸收层，用以吸收硫化氢气体，防止管道发生渗透；SoluForce 公司生产的SoluForce Gas Tight（GT）管道［18］引入了铝箔阻隔层，这种管道结构不但可降低气体渗透引起的屈曲失效风险，而且在传统输送领域应用之余，还可用于运输氢气等密度较低的气体。此外，这种结构不需要特殊处理，降低了安装和维护成本。

为了明确增加了铝箔阻隔层的高阻隔非金属柔性复合管的承压状态，分析阻隔层宽度、厚度以及缠绕角度等参数对复合管承压性能的影响，本文采用有限元模拟管道在内压作用下的应力变化，探究阻隔层参数与管道承压性能之间的关系，从而获得铝箔阻隔层的最佳几何及工艺参数，为保障管道的安全性及稳定性提供指导。

1 有限元模型的建立

1.1 高阻隔非金属柔性复合管结构及相关参数

高阻隔非金属柔性复合管的结构共分4 层，如图1所示，由内到外分别为内衬层、铝箔缠绕层、纤维增强层、外保护层，其具体几何参数见表1。内衬层和外保护层材料为高密度聚乙烯，纤维增强层是芳纶纤维合成股，阻隔层采用的是H18态铝箔。内衬层和外保护层保护中间纤维增强层面不受内部运输的气液介质和外部环境的腐蚀破坏；纤维层是管道的主要承载层；阻隔层起到阻隔管道气体渗透的作用。各层性能参数分别见表2和表3。

表1 高阻隔非金属柔性复合管几何参数Tab.1 Geometric parameters of non-metallic composite coiled tubes for hydrogen transport

表2 铝箔及管道内外层材料参数Tab.2 Aluminum foil and pipe inner and outer layer material parameters

表3 芳纶纤维力学参数Tab.3 Mechanical parameters of aramid fibers

图1 高阻隔非金属柔性复合管的结构简图Fig.1 Structure diagram of non-metallic composite coiled tube for hydrogen transport

1.2 建模方式

1.2.1 数学模型准则

复合材料层是由方向角不同的单层叠加而成的层合壳体结构，校核时必须依据单层的失效准则，用以判断单层在偏轴向应力作用或平面应力状态下是否失效的准则。 准则模型如下：

（1）最大应力准则

式中Xt——纵向拉伸强度

Yt——横向拉伸强度

Xc——纵向压缩强度

Yc——横向压缩强度

S——面向剪切强度

（2）最大应变准则

最大应变准则认为复合材料在复杂应力状态下进入破坏状态的原因是：方向的应变值达到了各基本强度值所对的应变值。

式中εxt——纤维方向允许的最大拉伸应变

εxc——纤维方向允许的最大压缩应变

εyt——垂直与纤维方向允许的最大拉伸应变

εyc——垂直于纤维方向允许的最大压缩应变

γs——平面最大剪切应变

（3）蔡-希尔（Tasi-Hill）准则

X、Y是正交各向异性材料1、2 主方向的基本强度；S是对材料1主方向施加的载荷。

1.2.2 结构模型建立

依据高阻隔非金属柔性复合管实际尺寸及结构特征，按某工厂传统的生产工艺，建立复合管的有限元模型如图2 所示。首先利用软件Part 模块构建管道各层结构，其次在Property 模块中为各结构层赋予对应的材料属性。采用复合材料均质化Halpin-Tsai模型法［19］模拟管道的纤维增强层，即将管道整个增强层视为一种正交各向异性的均质材料交错缠绕而成，6条芳纶纤维以±55 °由内向外缠绕堆叠，如图3 所示。其次在Assembly 模块中将各个结构层进行装配组合，得到整体管道模型结构。

图2 高阻隔非金属柔性复合管有限元模型Fig.2 Finite element model of non-metallic composite coiled tube for hydrogen transportation

高阻隔非金属柔性复合管各层之间存在非线性接触，因此对较厚的内、外PE 管采用C3D8R 实体单元。由于铝箔阻隔层的厚度很薄，为了提高计算效率，阻隔层的属性设置为壳（Shell）单元但定义其实体的厚度为0.05 mm。在Mesh 模块中，阻隔层中四边形区域通过S4R 单元类型划分网格，端部则以三角形单元S3 划分网格，这是为了使阻隔层中间主体区域划分的网格为规则四边形，从而提高模型收敛性。阻隔层网格划分如图4所示。

图4 阻隔层网格模型Fig.4 Barrier layer mesh model

1.3 接触关系与边界条件

为考虑层与层之间的滑移现象，有限元模型中阻隔层与内衬层和增强层之间的接触定义为“surface to surface”，摩擦因数取0.3。将接触中自身刚度较大的阻隔层定义为主面，自身刚度较小的内衬层和增强层定义为从面，各层之间的法向相互作用则定义为“hard contact”（硬接触），以避免在加载过程中模型相邻两层之间出现“穿刺”现象。

研究管道在内压载荷下的力学性能，需对管道模型进行边界约束。在管道一端部截面圆心处建立参考点RP1，将参考点与管道端部截面耦合并设置其边界条件为全向约束；管道另一端部截面与另一参考点RP2 耦合并设置其边界条件为仅开放轴向自由度，允许复合管在内压作用下沿管道轴向发生收缩。

1.4 载荷施加

在定义好模型的属性、网格以及约束等条件后，对管道内壁施加内压载荷，根据圣维南原理，一般认为管道的长度在10~20 倍外径范围内，便可忽略管道端部因连接或者固定约束导致的应力集中即端部效应，且可以认为管道受到的载荷是均匀的。本文取管道的1.5 倍公称压力（4.5 MPa）进行模拟计算，采用静态分析步计算，内压载荷大小从0 开始匀速增加，得出对应内压下各结构层的应力状况。

1.5 数据处理

根据所得到的各结构层应力云图，输出各参数变化条件下阻隔层的应力数据，并将所得到的数据在Origin 中绘制成折线图，观察数据变化情况，观察阻隔层各参数的影响规律。

2 复合管承压性能的模拟结果及分析

2.1 复合管各层受力情况

基于上述管道模型进行内压载荷作用下的有限元模拟，获得4.5 MPa（1.5 倍公称压力）内压下高阻隔非金属柔性复合管各结构层的应力云图，如图5所示。

图5 内压4.5 MPa下各结构层的应力分布Fig.5 The stress distribution of each structural layer under internal pressure of 4.5 MPa

由图5 各层应力云图可以看出，在内压载荷作用下，随着芳纶增强层铺层顺序的增加，其对应的应力依次有所降低，如第一层与第六层的应力分别为115.26 MPa 和112.24 MPa。而内外聚乙烯层的应力分别为6.87 MPa 和3.06 MPa，远远小于增强层的应力，这与张尹［20］研究RTP 管在内压载荷下的应力状态一致。铝箔阻隔层的应力为77.41 MPa，小于芳纶增强层的应力，但比内外层的应力大。说明高阻隔非金属柔性复合管在承受内压载荷时，芳纶增强层是管道的主要承载部分，且芳纶增强层的承载能力由内向外逐步降低，这与未添加阻隔层的非金属柔性复合管的应力规律一致。

不同内压载荷下高阻隔非金属柔性复合管各结构层的应力变化情况如图6所示。可以看出，随着内压载荷的不断增加，复合管各结构层的应力值呈线性增长趋势，但增大的幅度不同。且随着内压载荷的增大，芳纶增强层首末层的应力差［图6（e）］也不断增大，与相关研究［6，20-21］结果一致，因此可将增强层第一层的应力值作为增强层是否失效的判断依据。铝箔阻隔层的应力值小于增强层，且增强层所承受应力远小于其极限值，故可将铝箔阻隔层的最大Mises应力值作为判断管道是否会发生渗透的依据。

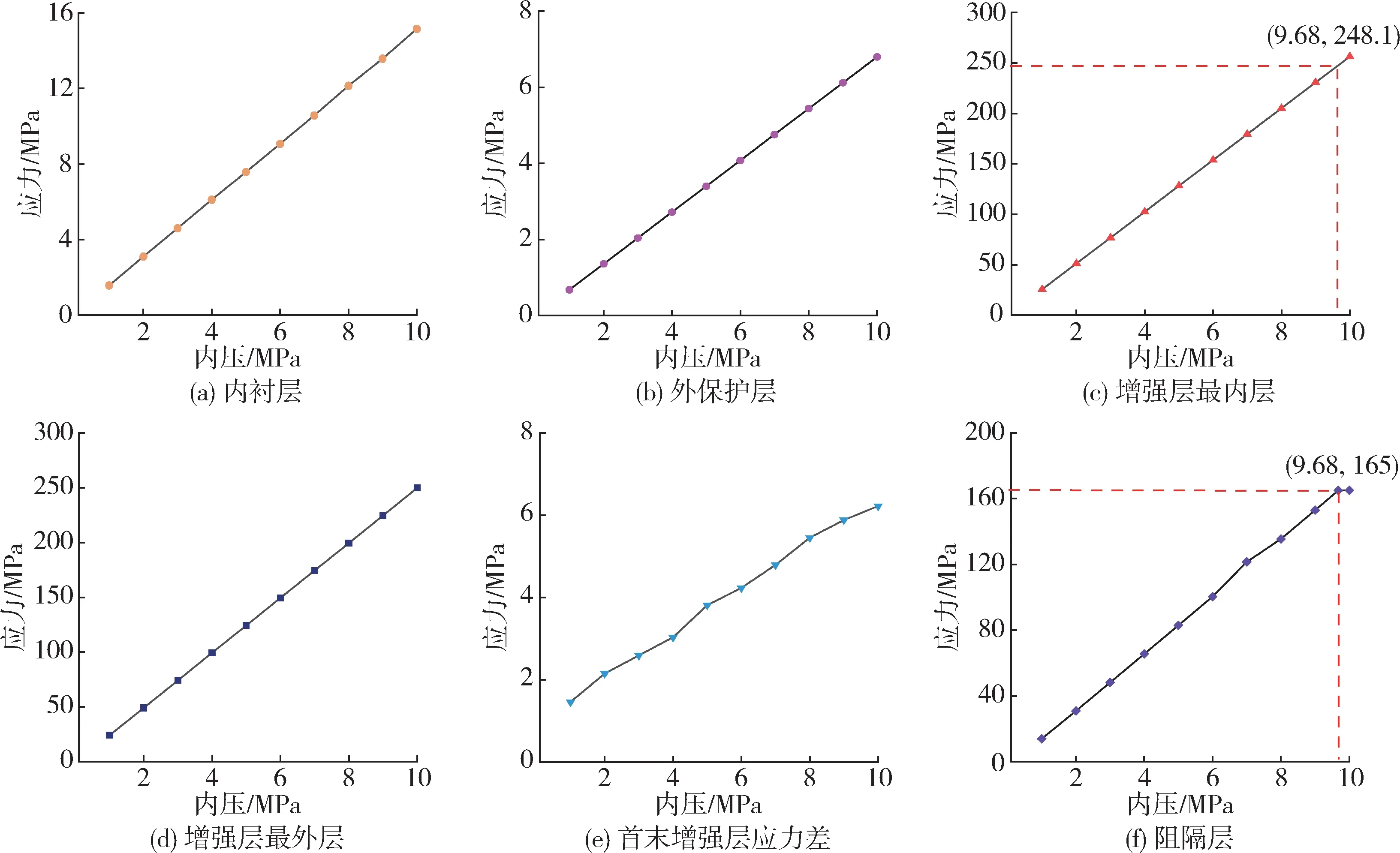
图6 不同结构层应力随内压载荷的变化曲线Fig.6 The stress curves of different structural layers with internal pressure load

为了确定高阻隔非金属柔性复合管在保证不发生渗透的情况下的最大应力，依据阻隔层在内压载荷下的极限应力值作为其判断依据。如图6（f）所示，当阻隔层达到其拉伸强度165 MPa 时，计算得出此时复合管所承受的内压载荷为9.68 MPa，即保证复合管不发生渗透的极限内压为9.68 MPa。同时，在9.68 MPa内压下，芳纶增强层的应力为248.1 MPa，远小于芳纶极限值，此时管道不会发生破坏失效。

2.2 铝箔的不同工艺参数对复合管承压性能的影响

如上所述，芳纶纤维增强层是复合管的主要承压层，在9.68 MPa 内压载荷作用下，芳纶纤维层应力远小于其极限值，故不考虑管道爆破失效的情况，但铝箔此时已达到其拉伸强度极限，可能会使管道发生渗透现象。因此，为了探究满足复合管渗透条件下的应力状态，只需考虑铝箔阻隔层的应力变化，即探究铝箔阻隔层的工艺参数对复合管承压性能的影响，从而获得最佳铝箔工艺参数。

2.2.1 铝箔厚度对复合管承压性能的影响

保持管道内径不变，同时固定铝箔阻隔层的宽度、各层之间摩擦因数以及缠绕角度等参数（铝箔宽度100 mm，摩擦因数0.3，缠绕角度49.63°），4.5 MPa 内压下，阻隔层应力状况随铝箔厚度变化的规律如图7所示。随着铝箔厚度的增加，芳纶增强层的应力略有增加，内衬层和外保护层所承受的应力均有所降低，但整体变化都不大。而铝箔阻隔层的应力先迅速降低后趋于平缓，降低幅度为13.2 %。图8 为阻隔层极限承压值随铝箔厚度变化曲线，可知随着阻隔层厚度增加，其极限应力先迅速增加后趋于平缓，表示其极限承压能力不断增强，故增加铝箔厚度，有助于防止管道发生渗透。综合考虑成本及管道性能的影响，选择管道各结构层应力最小所对应的阻隔层参数值，故选择0.15 mm作为阻隔层最佳厚度。

图7 不同复合管结构层应力随铝箔厚度的变化曲线Fig.7 Stress of different composite pipe structures against thickness of aluminumfoil

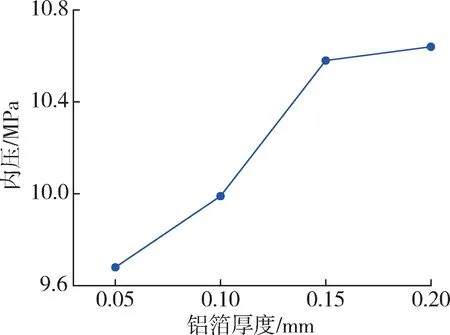
图8 阻隔层极限承压值随铝箔厚度变化曲线Fig.8 The limiting pressure value of barrier layer against the thickness of aluminum foil

2.2.2 摩擦因数对复合管承压性能的影响

根据管道实际使用以及建模情况，铝箔阻隔层为各向同性，故在建立模型时考虑了铝箔阻隔层与各层间的滑移情况，在各层接触间定义摩擦属性，设置摩擦因数。图9分别为不同摩擦因数，4.5 MPa内压载荷下的铝箔层以及芳纶层的应力变化情况。由图所知，铝箔阻隔层所承受的应力随摩擦因数增大而降低；而芳纶增强层所承受的应力逐渐增加，且增加幅度逐渐变小。但两层的整体变化都相对较小，故摩擦因数对复合管的承压性能影响相对较小。

图9 不同复合管结构层应力随摩擦因数的变化曲线Fig.9 Stress of different composite pipe structures against friction coefficient

2.2.3 铝箔宽度对复合管承压性能的影响

保持复合管内衬层、芳纶增强层和外保护层的各个参数不变，研究阻隔层铝箔宽度对复合管承压性能的影响。图10 为4.5 MPa 下，不同铝箔宽度（50~250 mm）复合管的铝箔阻隔层和芳纶增强层的应力状态。由图可知，随着铝箔宽度的增加，铝箔层所承受的应力有所降低，在200 mm 宽时降至最低，随即略微升高；而芳纶增强层的应力变化无明显规律，且变化幅度很小，不超过1 MPa。故铝箔层宽度的增加，可略微降低阻隔层应力，对增强层无太大影响。因此综合考虑管道应力变化，选择管道各结构层应力最小所对应的阻隔层参数值，最佳铝箔宽度定为200 mm。

图10 不同复合管结构层应力随铝箔宽度的变化曲线Fig.10 Stress of different composite pipe structures against width of aluminum foil

2.2.4 铝箔缠绕角度对复合管承压性能的影响

纤维增强塑料复合管设计中有一项指标是增强层纤维的缠绕角度，故高阻隔非金属柔性复合管需考虑铝箔阻隔层的缠绕角度，即铝箔缠绕方向与复合管轴向的夹角。图11 为4.5 MPa 内压载荷下，不同铝箔缠绕角度时，复合管的铝箔阻隔层和芳纶增强层所承受的应力变化曲线。随着缠绕角度的增加，铝箔阻隔层的应力不断降低：缠绕角度在10 °~50 °之间应力缓慢降低；在50 °~70 °之间迅速降低；70 °之后应力略微增加。芳纶增强层应力在114~115 MPa 之间波动变化，变化幅度不大。故可认为随着铝箔阻隔层缠绕角度的增加，铝箔阻隔层的应力略微下降，芳纶增强层应力无明显变化。因此综合考虑管道应力变化情况，选择管道铝箔阻隔层应力最小所对应的阻隔层参数值，故选择70 °作为阻隔层最佳缠绕角度。

3 结论

（1）采用Halpin-Tsai 模型法，利用ABAQUS 软件建立了DN150-PN3 MPa 高阻隔非金属柔性复合管模型，利用该模型计算得出复合管各结构层应力状况，芳纶增强层应力最大，其次为铝箔阻隔层，内衬层和外保护层应力最低，与实际应力情况一致。

（2）基于复合管有限元模型分析了铝箔阻隔层工艺参数对复合管承压性能的影响，发现铝箔层厚度对复合管承压性能影响最大，其次为摩擦因数的影响，铝箔层宽度和缠绕角度的影响最低。

（3）根据模拟结果，得到铝箔的各参数变化的对管道应力的影响规律。为了使复合管承压能力最强，应选择管道各结构层应力最小所对应的阻隔层参数值，可确定铝箔阻隔层的最佳参数为：铝箔厚度为0.15 mm，铝箔宽度为200 mm，缠绕角度为70（°）。