相图中自由度的理解*

陈香李，王伟涛

(陕西科技大学化学与化工学院，陕西 西安 710021)

相平衡(phase equilibrium)在生活中随处可见，相平衡相关知识广泛应用在实验室和工业生产中，如蒸馏、沉淀、结晶、萃取、气体在固体催化剂表面的吸附等；因此，物理化学中相平衡部分的知识与材料、冶金、化工等学科交叉融合较多，是极具实际应用性的一章。相平衡系统中，在不改变平衡态相的数目前提下，系统中可以独立改变的强度量个数称为自由度(degree of freedom)[1]。自由度可以理解为在保持系统相数不变的条件下，可以任意改变的独立变量数目，这些强度量的改变不会引起旧相的消失和新相的生成。平衡系统中，自由度=描述平衡系统的总变量数-平衡时变量之间必需满足的关系式的数目[2]。自由度的计算则依据相律公式f=C-P+n，式中的f代表自由度，C代表独立组分数(number of independent components)，P代表相的个数(number of phases)，n代表系统受到温度、压力、磁场、电场等影响系统平衡状态的外界因素个数。在一般的相平衡研究中，n值取2，即代表温度和压力。

为了表达多相系统的状态，人们常常用图形来表示系统存在的状态与组成、温度、压力等因素的关系，这种图形称为相图。一般的相图中，自由度通常代表的独立变量为组分浓度、温度和压力等。在相图的学习中，要求学生掌握自由度的概念、利用相律计算各个相区的自由度。学生在利用相律公式计算相图中的自由度过程中普遍存在一些疑惑，如自由度怎么计算、自由度的数值具体代表的是什么独立变量等问题。针对这些问题，本文重点介绍常见的单组分和二组分相图中相区、相线及特殊相点处自由度的计算方法及自由度所代表的意义。

1 单相区的自由度

图1是常见的气-液二组分相图。在该相图中，由于压力是常数，所以相律公式为f=C-P+1。单相区①(气相)和③(液相区)的自由度f=C-P+1=2-1+1=2，得到的自由度为2，意味着在单向区①和③中有两个可以独立变化的物理量，这两个可以独立变化的物理量为温度T和组成x，即在一定的范围内，这两物理量单独改变均不会改变其单相相态。

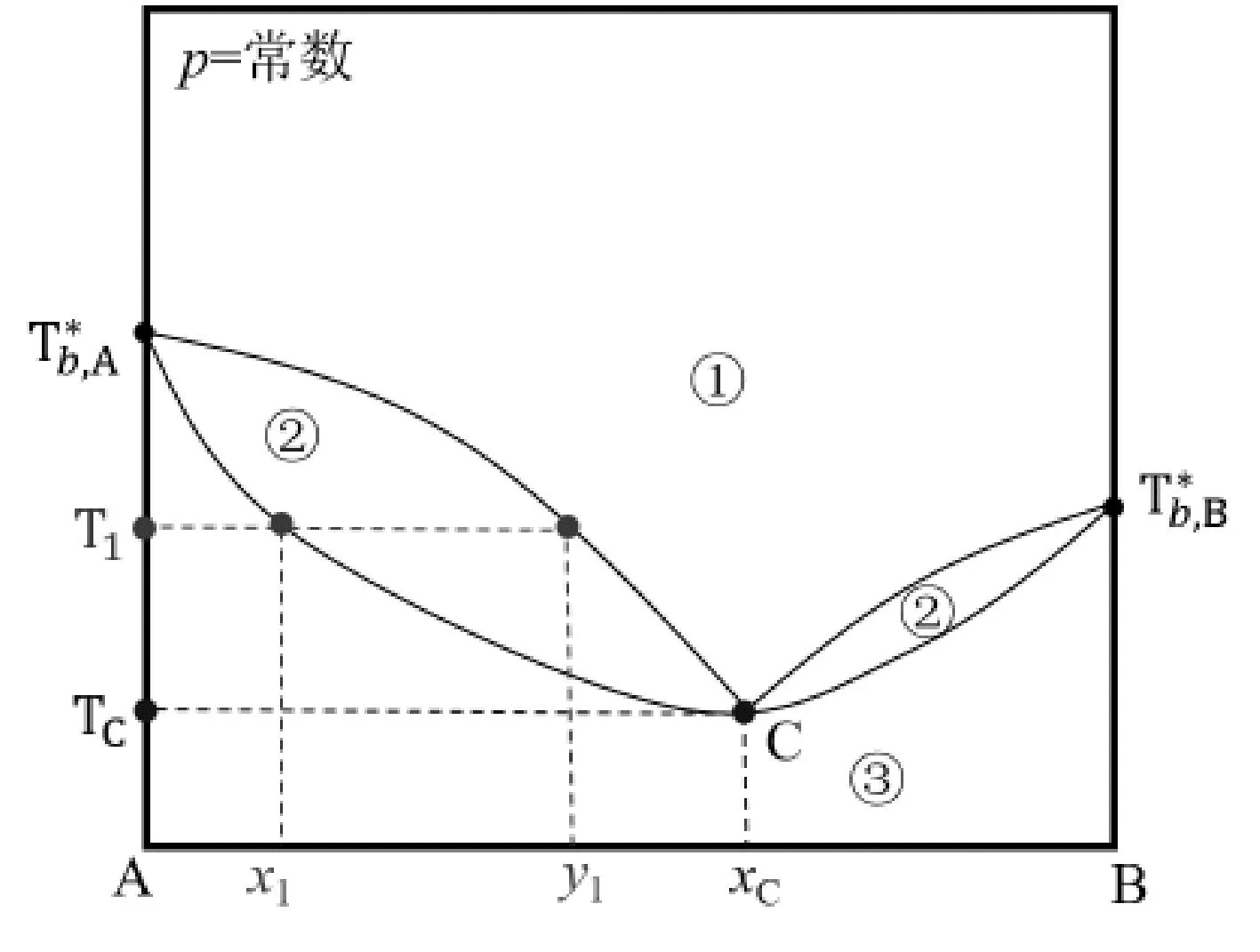
图1 气-液二组分温度-组成相图Fig.1 The temperature-composition liquid-vapor phase diagram for two-component

2 两相区的自由度

在图1中的气-液两相区②内，其自由度f=C-P+1=2-2+1=1。在两相区内，在保持气-液两相相数不变的情况下，可以独立改变的物理量是1个。对于这一个独立变量，很多同学会提出疑问：在相区②内，纵坐标温度T和横坐标组成x分别改变时，物系点仍然落在相区②内；所以温度T和组成x可以独立改变，自由度应该是2。这与根据相律计算得到自由度1相矛盾。实际上，在气-液两相平衡区域②内，当温度给定时，如图1中的T1，此时对应的气相组成和液相组成均为定值，分别y1和x1；虽然描述气-液两相区有3个参数：温度T1、气相组成y1、液相组成x1，但这3个参数中独立的变量只有1个，其余两个量只是因变量。在这个问题中，学生对“组成”的概念理解有误。在相区②内，自由度计算时我们所说的组成是“气相组成”和“液相组成”，而非“总组成”。图1中温度为T1时，对应的气相组成y1和液相组成x1是定值，总组成可以在x1和y1之间自由取值；只不过总组成改变时气相的总量和液相的总量会随之而改变，但是气相组成和液相组成不变。所以，可以这么说，在温度一定时，总组成在一定范围内改变，不会改变气相组成和液相组成。

3 相线上的自由度

图1中液相线和气相线上存在气-液两相。由于压力恒定，所以相律公式为f=C-P+1=2-2+1=1。在气相线(或者液相线)上，温度和气相组成(或液相组成)是一一对应的，其能够独立改变的量只有一个温度或者气相(或液相)组成，所以其自由度代表的是温度或者气相(或液相)组成。

图2是部分互溶系统的二组分气-液相图。在T1温度时存在的水平线L1GL2是三相线，在该三相线上共存l1、l2、g三相，其自由度f=C-P+1=2-3+1=0。自由度为0意味着在三相线上可以独立改变的物理量是0个。在三相线上(三相共存时)，加热时液相l1和l2按照两个线段的长度GL1和GL2的比例蒸发为组成为G点的气相，因此，液相l1和l2的组成始终分别为x1和x2，气相组成始终为xg；只不过液相l1和l2的量按比例在减少，气相的量在增大；但相数还是3相，没有发生变化，为l1、l2和气相。有同学就提出，三相线是一条水平的直线，在T1温度时，当改变横坐标即组成时，坐标点其仍然在线上，仍然保持三相不变，所以独立变量是1。在这个问题中，学生同样对“组成”的概念理解有误。我们所说的组成是各相中的组成，而非“总组成”。只要在三相线上，不论总组成如何，其三相的组成均是一定的：l1液相对应的组成为x1、l2液相对应的组成为x2，气相对应的组成为xg。

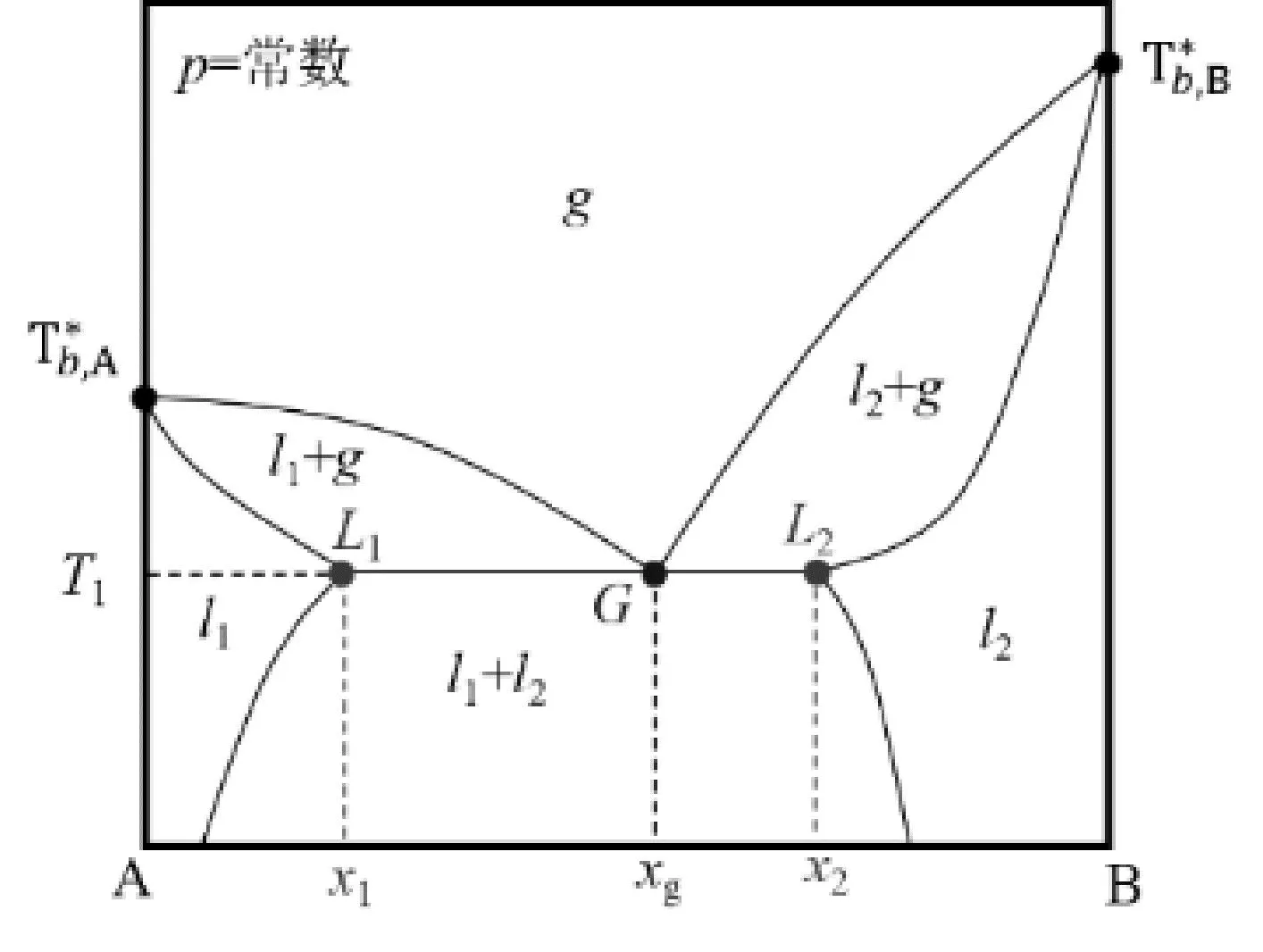
图2 部分互溶系统的二组分气-液温度-组成相图Fig.2 The temperature-composition liquid-vapor phase diagram for two partially miscibleliquids

4 相图上某些特殊点的自由度

(1)二组分气-液相图中共沸点的自由度

二组分气-液在共沸点时，其对应的压力、温度、组成均是一个定值，其自由度是0。但是，学生根据相律计算f=C-P+1=2-2+1=1。这显然和实际情况不相符。对此，有人提出[3]在相律推导时，没有考虑到平衡气相组成和液相组成相等这一条件，所以需要将相律修正为f’=C-P。笔者并不赞成这种处理方式。首先，相律公式中的n代表的是能够影响系统平衡的外界因素，如温度、压力、电场等。很显然，在图1共沸点时只存在一个影响平衡的外界因素温度。第二，共沸点时气相组成和液相组成相等这一条件属于强度变量之间的一个关系式。独立组成数计算式C=S-R-R’，其中S为物种数，R为独立反应数，R’为除化学反应外的其他限制条件数[4]或强度变量之间的关系式[5]或独立浓度限制条件[6]。共沸点处的气相和液相组成相等条件属于平衡限制条件。共沸点独立组分数C=S-R-R’=2-0-1=1，所以f=C-P+1=1-2+1=0。

(2)单组分的三相点和临界点

图3a为单组分纯物质的p-T相图。对纯物质，在三相点C时，其对应的相数是3，此时对应的相律计算公式为f=C-P+2=1-3+2=0。自由度为0。

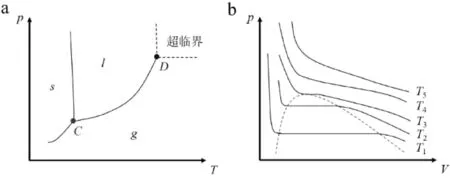
图3 单组分系统的p-T图(a)和实际气体的p-V图(b)Fig.3 The pressure-temperature for one-component (a)and pressure-volume phase diagram for real gas(b)

对纯物质，在临界点时气相和液相的一切差别均消失掉了，气液相界面消失，没有明显相界面。此时气液两相的摩尔体积及其他性质完全相同。在临界点时，对应的有临界温度T和压力P，其均为一个定值，故自由度应该为0；但是根据相律公式f=C-P+2=1-P+2=3-P，不论临界点处是一相还是两相，其自由度都不可能为0；此时存在矛盾。因此，在根据相律计算时，必然有一些限制条件没有考虑到。

气液相界面消失，没有明显相界面，符合一相的定义，此时应该按照一相计算。要找出其中还存在的限制条件，需要从单组分系统的p-V相图来看。如图3b所示，实际气体的p-V图。在临界点时，从数学上看应该满足压力对体积的一阶导数和二阶导数等于0[7]，即

如果气体符合范德华方程，那么就可以根据上面两式求解，得到

Vm，c=3b

因此，在临界点使用相律时存在两个独立限制条件，应该减掉这两个独立限制条件温度和压力，或者在临界点时，相律公式应该是f=C-P。此时，对应的自由度则为f=C-P=1-1=0，与实际情况相一致。

(3)二组分系统的三相线的两个端点

在图2中的三线端点L1(或者L2)处，其对应的相态应该是l1、l2、g，但是此点处的l2(或者l1)和g的量是无限小[8]，此时，根据相律计算f=C-P+1=2 -3+1=0。

图3中的三相线的端点C(或者D点)，对应的是纯物质冰(或者纯硝酸铵)，所以其对应的相态应该是纯物质冰和液体，所以其相数是2，对应的相律公式计算为f=C-P+1=1-2+1=0，其自由度为0。图3中的F点，其对应的相态为3相，为等轴晶相的硝酸铵、立方晶相的硝酸铵及液相，所以其自由度为f=C-P+1=2-3+1=0。但是在F’点处，其组成是纯硝酸铵，此时存在的相态是等轴晶相和立方晶相硝酸铵两相平衡，所以其自由度为f=C-P+1=1-2+1=0。

(4)二组分部分互溶液体的会溶点

图4a为二组分部分互溶液体的相图。在加热过程中共轭溶液的组成逐渐接近，在一定温度时，两相的组成完全相同，因此两个共轭溶液之间的相界面消失，成为均匀的单一液相，即图中T1对应的C点，该点则称为会溶点。从相图上看，在压力一定时，会溶点对应的温度和组成都是定值，所以其自由度显然为0；但是根据相律该点处的自由度为f=C-P+1=3-P，计算的自由度无论如何都不能为0。该结果与实际相矛盾。对此，有人提出在会溶点时可以看成两相，两个共轭溶液之间的浓度相等，即存在着特殊的浓度限值条件[9]，所以相律的计算公式应该是f=C-P+1-R’=2-2+1-1=0。但是，实际上在会溶点两个共轭溶液的浓度一样，所以必然是一相；如果是一相，就不存在浓度相等的限值条件了。因此，在会溶点时，必然存在其他的独立限制条件。图4b表示的是恒温恒压下组分A的化学势μA随组成xB的变化曲线[10]。图4b中有3条等温线，会溶点对应的是Tc曲线的c点。该点处满足

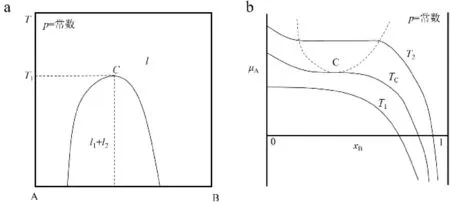
图4 二组分部分互溶液体的温度-组成相图(a)和化学势-组成(b)的变化Fig.4 The temperature-composition liquid-liquid phasediagram (a)and chemical potential-composition diagram (b)for two-partially miscible liquids

这两个等式求解可以得到会溶温度和组成[10]，即为会溶点处两个独立性的特殊限制条件。因此，相律计算式应该为f=C-P+1-R’=2-1+1-2=0。

(5)生成不稳定化合物系统的不相合熔点

图5为具有不相合熔点的二组分固-液相图。由于A和B生成的化合物C不稳定，因此在图中T1温度时D点处化合物C开始分解为A和B。在该温度下，B在A中的溶解度为L’点处对应的组成xb’，而C物质中所包含的B的量大于组成大于xb’，此时C物质分解时产生的B的量大于其溶解度，故有B物质固体析出，即，C(s)→A(s)+l；因此D点处对应的相态为纯B固体和溶液(A和B组成的溶液，溶液组成为xb’)。C物质是A和B组成的化合物AmBn，那么溶液中的B物质的量加固体B的量与A的量的比值应该符合n/m，因此，在该点处存在一个特殊的限制条件。因此，相律计算式为f=C-P+1-R’=2-2+1-1=0。

图5 生成不稳定化合物系统的固-液相图Fig.5 Phase diagram compound formation with incongruent melting point for solid-liquid

5 结 语

相图中的自由度概念的理解和计算是物理化学课程中相平衡部分的知识重难点，让学生充分理解单组分和二组分相图中相区、相线及特殊相点处的自由度的计算方法及自由度所代表的意义对于学生掌握自由度的概念、利用相律公式计算相图中的自由度具有重要的指导意义。相图中自由度对应的独立变量一般为温度、压力、组成；在运用相律公式进行自由度计算时，需要仔细分析其中存在的特殊限制条件，得到的自由度数应符合实验事实。