开槽形孔的波纹钢腹板弹性剪切屈曲性能研究*

姚永红 徐二满

(安徽理工大学 安徽淮南 232001)

波纹腹板钢结构是指将普通钢构件中的平钢腹板或其他材料的腹板替换成波纹状钢腹板的结构。波纹腹板钢结构应用比较广泛，具有较好的抗剪性能，在工程中可以通过替代传统钢构件的应用来降低材料的使用量，从而节省成本。目前应用较为广泛的波纹腹板形式主要是梯形波纹腹板和正弦曲线波纹腹板。对于波纹钢腹板的剪切屈曲性能研究，各国学者已经有了较为深入的探索，所总结的理论也较为成熟。Timoshenko最早利用平板理论，结合能量法推导出波纹腹板弹性局部屈曲应力计算公式[1]，Skan和Southwelll两位学者则在此理论基础上进一步研究，得出目前应用较为广泛的弹性局部剪切屈曲应力公式[2]。美国学者V. Hlavacek通过研究平钢板的剪切屈曲理论，认为平钢板的弹性整体屈曲计算方法同样能够用于计算波纹钢腹板的弹性整体剪切屈曲计算，由此提出了波纹钢腹板弹性整体剪切屈曲的计算公式[3]，Galambos等则在此基础上提出了针对不同约束方式的整体屈曲边界条件系数[4]。但是目前对于波纹钢腹板开孔后的剪切屈曲性能研究相对较少，且开孔多以圆孔为主，对于其他形式孔洞的研究也相对较少。李国强、邱介尧等讨论了波纹腹板开圆孔H型钢的抗剪性能，主要分析了开孔尺寸和开孔位置对弹性剪切屈曲性能和弹塑性剪切屈曲性能的影响[5-6]；张旭乔等则研究了波浪形波纹腹板开圆孔后对构件应力分布情况和抗剪承载力的影响[7]。在实际工程应用中，尤其是钢结构领域，为铺设管道和使用螺栓，槽形孔的应用十分广泛。因此，对开槽形孔的波纹钢腹板的剪切屈曲性能研究具有很强的实用意义。文章创新性地对梯形和正弦曲线两种波纹形式的波纹钢腹板开槽形孔，研究开孔尺寸对波纹钢腹板弹性剪切屈曲临界应力的影响，以满足实际工程中特定场景下的需求。

1 有限元模型验证

为验证有限元软件的有效性，选取尺寸参数不同的四组波纹腹板数据样本，并进行有限元建模。四组模型均选用Q355钢，均采用四边简支的约束方式，只改变波纹钢腹板的高度和波纹截面形状等尺寸参数。采用有限元数值模拟计算值与建议公式所得数值对比的方法进行验证。因不同学者对正弦曲线波纹腹板的剪切屈曲破坏形式和剪切屈曲临界应力表达式存在不同的理解，且梯形波纹腹板剪切屈曲临界应力公式较为成熟，由此，文章选用梯形波纹腹板剪切屈曲临界应力公式进行有效性验证。公式选用应用较为广泛的Skan-Southwell的弹性局部剪切屈曲临界应力表达式[2]和Galambos的弹性整体剪切屈曲临界应力表达式[4]。由于目前对于相关屈曲的研究不太统一，众多公式差异较大，且破坏模式相对复杂。因此，需合理选取四组样本模型的尺寸参数，减少因相关屈曲的产生对计算弹性局部剪切屈曲临界应力和弹性整体剪切屈曲临界应力的影响。

弹性局部剪切屈曲临界应力表达式[2]：

(1)

式(1)中，ks为反映局部屈曲的边界条件屈曲系数，当四边简支时，ks=5.34+4.0(w/hw)2；hw为波纹腹板高度；w=max{b，d/cosθ}；b为波纹腹板中平板段宽度；d为波纹腹板中斜板段宽度；θ为波纹腹板中斜板倾角；tw为波纹腹板厚度。

弹性整体剪切屈曲临界应力表达式[4]：

(2)

式(2)中，ks为反映整体屈曲的边界条件屈曲系数，Galambos定义简支边界条件下ks=31.6[4]；Dx为绕弱轴的面外弯曲刚度；Dy为绕强轴的面外弯曲刚度；hw为波纹腹板高度；tw为波纹腹板厚度。

将四组模型的有限元模拟计算数值与表达式计算数值汇总，汇总数据见表1。如表1所示，经计算后对比可发现，有限元软件模拟所得结果与表达式计算所得结果相比，误差均在10%以内。因此，有限元软件模拟计算波纹钢腹板构件的弹性剪切屈曲临界应力较为准确。

表1 有限元模拟与表达式所得剪切屈曲临界应力数值对比

2开孔波纹钢腹板有限元分析

2.1构件尺寸和材料的选取

为研究腹板开槽形孔对波纹钢腹板剪切屈曲性能的影响，需要先选取比较合适的腹板波形尺寸，文章选用《波纹腹板钢结构技术规程》CECS291：2011中已有的梯形波纹尺寸进行建模计算[8]，其波形截面及尺寸见图1。正弦曲线波纹腹板的波纹周期和波纹幅度选择与梯形波纹腹板的一致，正弦曲线波纹函数为y=25sin(πⅹ/120)，其波形截面及尺寸见图2。

图1 梯形波纹腹板截面尺寸图

图2 正弦曲线波纹腹板截面尺寸图

构件材料均选用Q355钢，弹性模量E=206GPa，泊松比υ=0.3。为使有限元模型尺寸能够符合实际工程应用场景中使用和防腐的需求，腹板高度与厚度的比值应满足hw/tw≤600，且tw=2～6mm。因此，文中有限元模拟选取的梯形波纹腹板和正弦曲线波纹腹板的高度均选为600mm，厚度均选为2mm。

2.2槽形孔尺寸的选取

为能够较为精确地收集数据，对槽形孔直径变量的步长选为10mm，对槽形孔长度变量的步长选为20mm。由此选取槽形孔直径为50mm、60mm、70mm、80mm、90mm、100mm；选取槽形孔长度为140mm、160mm、180mm、200mm、220mm、240mm。槽形孔形状及参数标注见图3。

图3 槽形孔参数标注图

2.3有限元模型的建立

在有限元软件中建立波纹腹板模型，选定波纹腹板的中心点作为槽形孔的形心。开孔后的波纹腹板见图4，正弦曲线波纹腹板开孔位置与梯形波纹腹板开孔位置相同。模型的网格划分尺寸选为10mm×10mm，该尺寸的网格经过试算发现具有较高的精度，且计算耗时相对较少。为使开孔处的网格单元计算更加精确，在开孔处单独进行网格划分，使开孔处网格更加均匀规则。

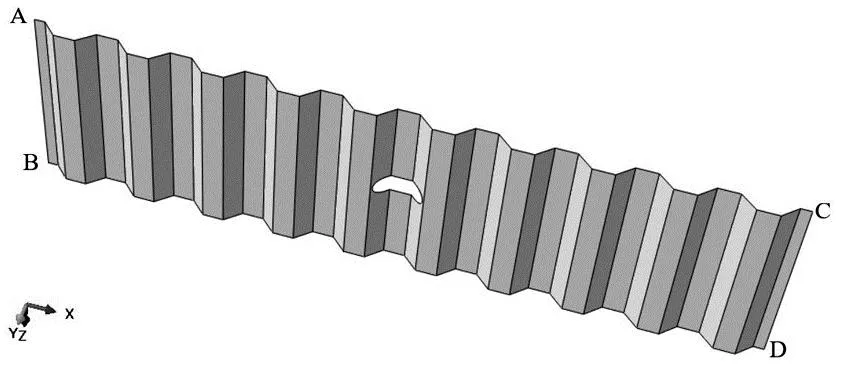
图4 波纹腹板开孔图

2.4 约束和加载方式

对有限元模型中的波纹钢腹板采用四边简支的约束方式。对AB边约束X、Y、Z方向的位移和Y方向的转角，对CD边约束Y方向的位移，AC、BD边作为腹板的折线边，约束其X、Y方向的位移。为使腹板承受剪力，选择在CD 边沿着Z方向进行加载。

3参数分析

改变开孔参数，进行多次建模分析。通过有限元软件计算出不同开孔参数下两种波纹形式钢腹板的弹性剪切屈曲临界应力。将两种波纹钢腹板的弹性剪切屈曲临界应力数据分别汇总到表格，汇总数据见表2和表3。为便于分析开孔的长度和直径对波纹钢腹板的弹性剪切屈曲临界应力的影响，将表2和表3数据分别绘制成点线图，见图5和图6。分别选取两种波纹钢腹板开孔直径为80mm，开孔长度为160mm、200mm、240mm的部分有限元模型的弹性屈曲效果图用以分析规律，屈曲效果见图7。

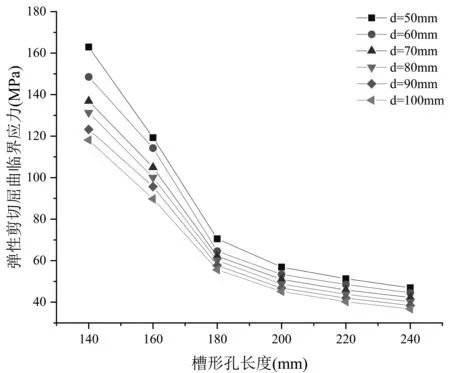
图5 开孔尺寸与梯形波纹钢腹板弹性剪切屈曲临界应力关系

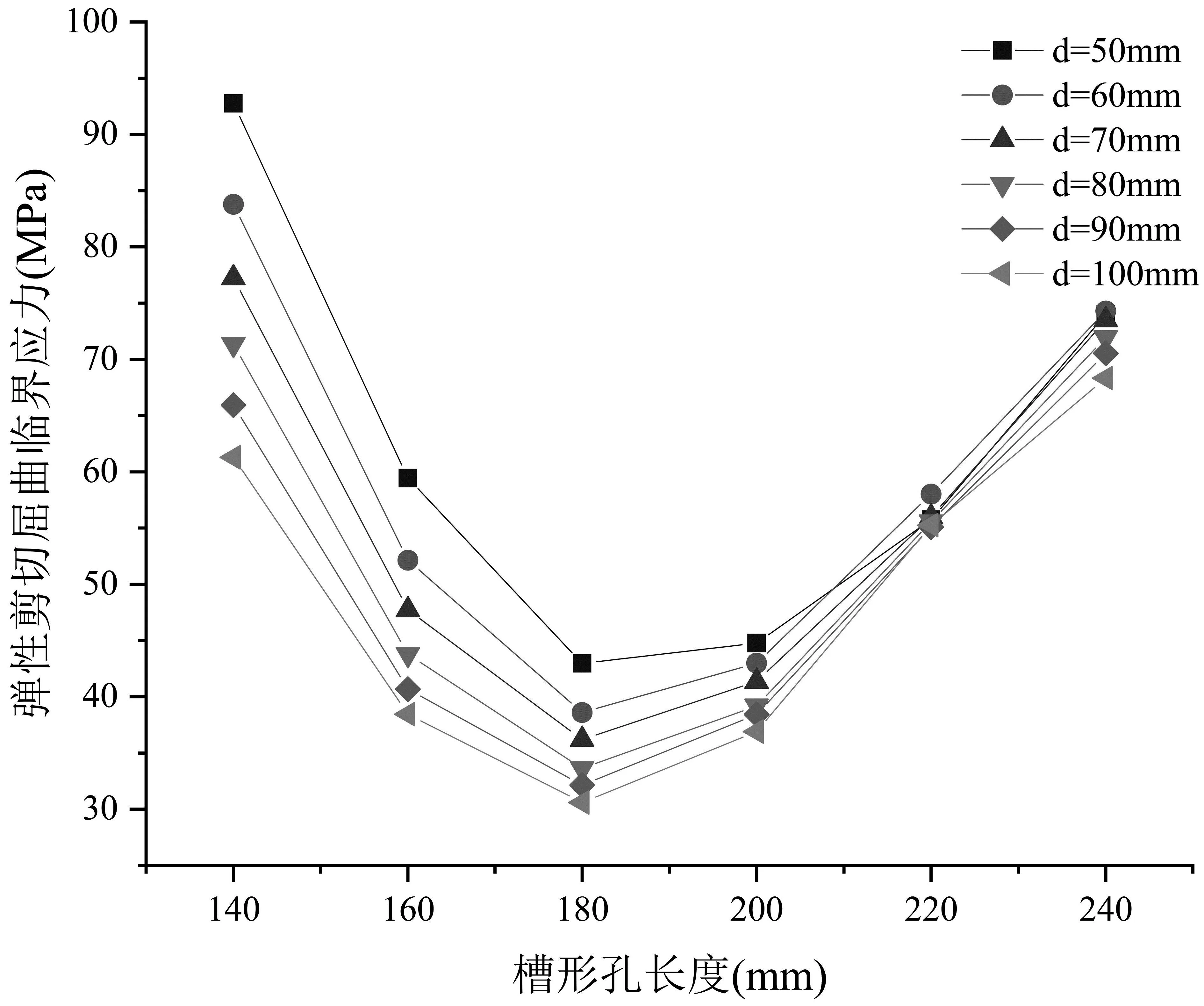
图6 开孔尺寸与正弦曲线波纹钢腹板弹性剪切屈曲临界应力关系

a1

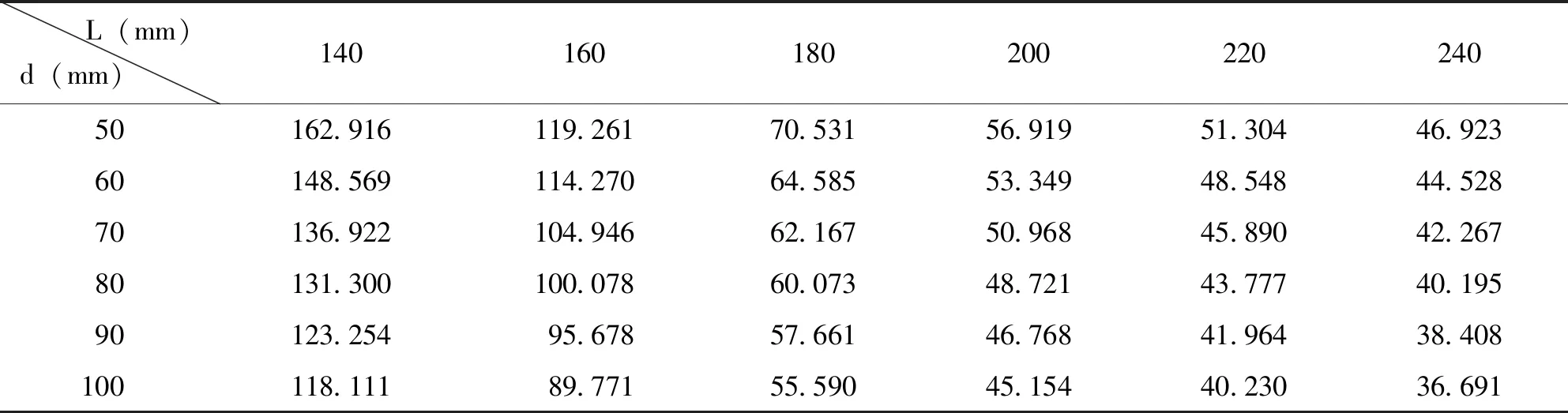
表2 有限元模拟梯形波纹钢腹板开孔弹性剪切屈曲临界应力(单位：MPa)

表3 有限元模拟正弦曲线波纹钢腹板开孔弹性剪切屈曲临界应力(单位：MPa)

3.1开孔前后对比分析

选取材料属性、尺寸以及波形截面与文章模型完全相同的梯形波纹钢腹板模型和正弦曲线波纹钢腹板模型，采用同样的约束方式和加载方式，在未开孔的情况下，经过建模分析计算，梯形波纹钢腹板模型的弹性剪切屈曲临界应力为767.823MPa，正弦曲线波纹钢腹板模型的弹性剪切屈曲临界应力为468.025MPa。与表3中开槽形孔后的波纹钢腹板模型应力数据对比可发现，其应力显著高于开孔后两种波形的波纹钢腹板的弹性剪切屈曲临界应力。由此可见，腹板开槽形孔对梯形波纹钢腹板和正弦曲线波纹钢腹板的弹性剪切屈曲临界应力均有着较大的影响。通过有限元模拟可发现，腹板开槽形孔后，梯形波纹钢腹板和正弦曲线波纹钢腹板发生弹性剪切屈曲破坏的位置均聚集于孔洞周围，这表明开槽形孔后，两种波形的波纹钢腹板更容易在开孔处发生弹性剪切屈曲破坏。

3.2开孔参数分析

从图5的曲线趋势分析表明，对于文章所给出的梯形波纹钢腹板，在槽形孔长度相同的情况下，槽形孔直径越大，构件的弹性剪切屈曲临界应力越低；槽形孔直径相同的情况下，槽形孔越长，构件的弹性剪切屈曲临界应力越低，但当槽形孔长度较大时，应力降低幅度会有所减缓。通过对图7a的屈曲效果图进行分析，发现最先发生屈曲的应力数值较大区域始终处于与中间平板相邻的两侧斜板上，斜板为承担应力作用的关键部分，因此，两侧的斜板对相邻的平板起到了加劲的作用。当开孔长度较小时，两侧斜板上孔洞面积随开孔长度的增大而增大，因此临界应力随开孔长度变化较为明显；当开孔长度较大时，两侧斜板上开孔面积趋于饱和，因此构件的临界应力随开孔长度变化较为平缓。从图6的曲线趋势分析表明，对于文章给出的正弦曲线波纹钢腹板，槽形孔直径相同的情况下，槽形孔越长，构件的弹性剪切屈曲临界应力越低，但当槽形孔较长时，弹性剪切屈曲临界应力会有一定程度的回升。通过分析图7b的屈曲效果图可发现，最先发生屈曲的应力数值较大区域始终处于波峰和波谷之间的斜波上，斜波为承担应力作用的关键部分。当开孔长度较小时，斜波上的开孔面积随开孔长度的增大而增大，因此，当开孔长度较小时，临界应力随着开孔长度的增大而减小；当开孔长度较大时，孔洞跨越到相邻的斜波中，多个斜波共同承担应力作用，因此，当开孔长度较大时，临界应力随着开孔长度的增大而有一定程度的回升。在槽形孔长度相同的情况下，槽形孔直径越大，构件的弹性剪切屈曲临界应力越低，但当槽形孔较长时，会有少量开孔直径大的模型的临界应力大于开孔直径小的模型的临界应力。分析图7b可知，开孔长度较大时，开孔直径增大会使孔洞在多个斜波中占据的面积变大，增大了多个斜波承担应力的范围。因此，开孔长度较大时，会有少量开孔直径大的模型的临界应力大于开孔直径小的模型的临界应力。

4结论

通过对波纹钢腹板进行有限元建模并分析，对比已有公式，验证了有限元软件数值模拟的有效性。通过改变槽形孔的尺寸参数，在有限元软件中进行模拟分析，研究孔洞尺寸参数对文章给出的两种不同波纹形式的波纹钢腹板弹性剪切屈曲强度的影响，其结论如下：

(1)梯形波纹钢腹板和正弦曲线波纹钢腹板开槽形孔后，其弹性剪切屈曲临界应力会有明显的下降，且发生屈曲的位置集中于开孔附近；

(2)梯形波纹钢腹板开槽形孔的长度较小时，斜板处开孔面积随开孔长度增大而增大，其弹性剪切屈曲强度随开孔长度增大而降低，且幅度较为明显，当槽形孔长度较大时，斜板处开孔面积趋于饱和，则弹性剪切屈曲强度的降低幅度会有所减缓；

(3)梯形波纹钢腹板开槽形孔的直径越大，其弹性剪切屈曲强度越低；

(4)正弦曲线波纹钢腹板开槽形孔的长度较小时，斜波处开孔面积随开孔长度增大而增大，其弹性剪切屈曲强度越低，当槽形孔长度较大时，多个斜波共同承担应力，则弹性剪切屈曲强度有所回升；

(5)正弦曲线波纹钢腹板开槽形孔的直径越大，其弹性剪切屈曲强度越低，但当槽形孔较长时，少量开孔直径大的模型由于在多个斜波上具有较大的开孔面积，增大了斜波承担应力的范围，其弹性剪切屈曲强度会大于部分开孔直径小的模型的弹性剪切屈曲强度。