博弈论：社会科学的物理学*

罗 君 刘轶群 刘敬伟

(1茅台学院工商管理系 贵州仁怀 564507；2维多利亚大学古斯塔夫森商学院加拿大维多利亚 V8W2Y2)

1研究背景

博弈论，是研究个体间策略性互动行为的理论，又称互动决策理论.由于社会是由个体(个人或组织)组成的，因此，博弈论已经深入到了社会科学的几乎所有领域，又因其数理分析的严密性，被认为是社会科学的物理学[1].

1944年，由冯·诺依曼和摩根斯坦合著的《博弈论与经济行为》(Theory of Game and Economic Behavioer，by John von Neumann and Oskar Morgenstern，1944)一书的出版，标志着博弈理论的初步形成.博弈论诞生的初期，主要以普林斯顿大学为研究中心，并逐渐扩散开来.博弈论的研究被分为两大分支：非合作博弈(Non-cooperative Game)与合作博弈(Cooperative Game)，1980年代为其成长爆发期，1994年诺贝尔经济学奖首次颁发给博弈论研究的奠基人约翰·纳什(John F. Nash)、海萨尼(John C. Harsanyi)和泽尔腾(Jr. Reinhard Selten)，以表彰他们对非合作博弈均衡所做的开拓性贡献.其中，纳什的贡献在于纳什均衡(Nash Equilibrium)，海萨尼的贡献在于不完全信息下的均衡性，泽尔腾则是对完美均衡(Perfect Equilibrium)作出了贡献[2].截至2022年度，诺贝尔经济学奖先后9次颁发给博弈论领域的学者，足见博弈论的魅力.

博弈论的主要研究领域有：①演化博弈论，主要源自梅纳德·史密斯和普瑞斯发表在Nature上的“动物冲突的逻辑”(The Logic of Animal Conflict，J.Maynard Smith and G.R.Price，1973)一文；②行为博弈论(behaviroal game theory)，通过考察人类非理性因素，研究参与人的策略选择问题，有实验博弈(在实验室进行的博弈)和实证博弈(在实际情景中进行的博弈；③算法博弈论，算法博弈论融合了计算科学与博弈理论，主要研究领域包括各种均衡的计算及复杂性问题、机制设计(包括在线拍卖、在线广告)、计算社会选择等；④组合博弈论(combinatorial game theory)主要研究具有完全信息的序贯博弈；⑤非贝叶斯博弈(non-bayesian games)，在放松传统博弈理论的贝叶斯假设下，探讨不确定性下的决策.

2 n人非合作博弈模型、解概念与范例

2.1模型

参与人i∈{1，2，…，n}有mi个行动策略，令si∈{1，2，…，mi}表示参与人i的选项，参与人i的支付(tradeoff)为ai(s1，s2，…，sn)，再令xi=(xi(1)，xi(2)，…，xi(mi))表示参与人i的策略分布(xi(·)非负且和为1)，亦即xi表示参与人i在其mi个行动策略中的概率分配.模型要解决的问题是，如何决定博弈中各个参与人的策略选择.

2.2解概念(solutions concepts)

纳什均衡解(nash equilibrium)与完美均衡解(perfect equilibrium)是非合作博弈的两个基本解概念.纳什均衡解(Nash，1950)是指：任一参与人在知道其他参与人的策略选择后，并不改变自己的策略选择；完美均衡解(Selten，1975)是指：在纳什均衡解中，那些明显不会被比下去而有可能被采用的策略，换句话说，有弱劣策略的纳什均衡不是完美均衡[3].

2.3范例

2.3.1情侣博弈 又称性别战(battle of sexes)，Ann和Bob是一对情侣，周末到了，Ann想去听一场难得的音乐会，而Bob想去看一场同样难得的足球赛，当然，两人不想分开，希望能在一起共度美好时光，怎么办呢？Ann(参与人1)和Bob(参与人2)各有两个选项：听音乐会(选项1)和看足球赛(选项2)，该博弈的支付矩阵如表1所示.

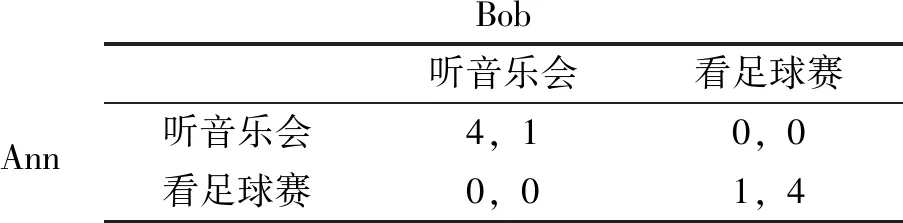
表1 情侣博弈支付矩阵

从以上博弈支付矩阵来看，如果两个人一起去听音乐会，Ann与Bob的效用分别为4，1；如果两个人一起去看足球赛，其效用分别为1，4；其他不在一起的组合，效用皆为0.

Ann和Bob各自的效用还可以用一个2×2矩阵A和B来分别表示：

该博弈有三个纳什均衡解，包括两个纯策略均衡和一个混合策略均衡：(1)x1=(1，0)，x2=(1，0).即两人都去听音乐会，Ann的效用为4而Bob为1；(2)x1=(0，1)，x2=(0，1).即两人都去看足球赛，Ann的效用为1而Bob为4；(3)x1=(4/5，1/5)，x2=(1/5，4/5).即Ann以4/5的概率去听音乐会，以1/5的概率去看足球赛，而Bob则以1/5的概率去听音乐会，以4/5的概率去看足球赛，Ann和Bob的效用皆为4/5(=4/5×1/5×4+1/5×4/5×1).这三个纳什均衡解同时也是完美均衡解，但完美均衡解并没有明确告诉Ann和Bob该采用三个解中的哪一个：Ann可以说服Bob一起去听音乐会，Bob也可以说服Ann一起去看足球赛，或者两人选择其实并无效率的混合策略，这需要参与人进一步协调和沟通.纳什均衡解的“唯一性”问题，至今尚未解决.

2.3.2非完美均衡解博弈 考虑如下两个参与人之间的博弈(各有两个选项)：

该博弈有两个纯策略纳什均衡解：(1)x1=(1，0)，x2=(1，0)；(2)x1=(0，1)，x2=(0，1).亦即，两人都采用选项1，或者两人都采用选项2，但前者明显劣于后者，也就是说前者明显能被后者比下去，因此前者虽然是纳什均衡解但不是完美均衡解.

2.3.3斗鸡博弈(chicken game) 又称胆小鬼博弈。两个参与人，各自驾车在一条道路上沿着路中间高速相向迎面而来，此时双方各有两个选项：选项1：避让(闪到路边)；选项2：不避让(沿着路中间继续高速前行)，各自的支付矩阵如下：

矩阵A和B互为对称矩阵，其中，相互避让的效用或支付为0(表示互不吃亏)，双方都不避让的效用或支付为-109(表示两败俱伤)，己方避让对方不避让为-10(表示不满对方的霸道)，己方不避让对方避让为1(表示占便宜).该博弈有三个纳什均衡解：①己方让对方不让；②己方不让对方让；③各自以99/100的概率避让，以1/100的概率不避让.在面对冲突(比如遭受侵略)时，要让对方强烈地相信己方会采取“不让”的策略，对方就越有可能采取“让”的策略.

2.3.4囚徒困境(prisoner's dilemma)[4]两个嫌犯(两个参与人)被警察隔离审讯，他们各自都有两个选项：选项1：认罪；选项2：不认罪.博弈的支付(表示判刑的时间)矩阵如下：

矩阵A和B互为转置矩阵，该博弈只有一个纳什均衡解：双方都认罪，各自被判处5年徒刑.虽然双方都不认罪(各自被判1年)对他们是最好的结果，但如果一方认罪另一方不认罪，不认罪的一方会被加重处罚，而认罪的一方则被免于处罚，因而存在被对方出卖的风险，从理性人的角度出发，都不认罪的选项无法形成纳什均衡解，两嫌犯只有在警察设计的诱因机制下认罪.

3 n人合作博弈的模型、解概念与范例

3.1模型

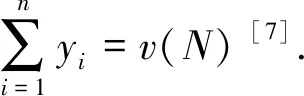
3.2解概念

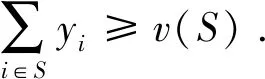
核中有多个解时，该如何选择呢？核仁便是核中的一个公平解.核仁(Schmeidler，1969)所依据的分配思想，是让一个群体中最不幸成员的幸福最大化，若有多重选择时，再使次不幸成员的幸福最大化，以此类推，直到找到一个解[9].这里所指的成员是任一个次级联盟(不含大联盟及空集)，共有2n-2个成员.

夏普利值是指(Shapley，1953)参与人的贡献以边际贡献来衡量，n个参与人共有n！个排列，某个参与人的分配值为其在n！个排列中的平均边际贡献[10].在一个排列中，令S(可为空集)表示排在参与人i前面的所有参与人，则参与人i在该排序中的边际贡献为v(S∪{i})-v(S).

3.3范例

三家公司拟成立合作研发中心，其中各个公司(1，2，3)单独研发，其成本分别为11、8、7；公司1、2合作研发的成本为14；公司1、3合作研发的成为为15；公司2、3合作研发的成本为13；公司1、2、3合作研发的成本为为20.那么，三家公司应如何公平分担合作研发的成本呢？

首先，将该问题表示为3人合作博弈模型：(1)v(φ)=0；(2)v({1})=v({2})=v({3})=0(因为单独研发没有节省成本)；(3)v({1，2})=5(公司1，2合作研发，可节省成本5(=11+8-14))；同理：(4)({1，3})=3；(5)v({2，3})=2；(6)v({1，2，3})=6.

其次，求该博弈的核：该博弈的核为以下不等式组的解集(由六个不等式和一个等式所围成的区域，如图1阴影部分所示)：

图1 合作博弈的核 (不等式组的解集)

再次，求该博弈的核仁：各成员(不包含大联盟和空集)的幸福值可以定义为其分配总值减去其联盟价值(见表2)，因为y1+y2+y3=6，因此由表2可知，成员{1}和成员{2，3}的幸福值之和为4，成员{2}和成员{1，3}的幸福值之和为3，成员{3}和成员{1，2}的幸福值之和为1.最不幸成员为{3}和{1，2}(他们的幸福值之和最小)，他们平分其幸福值，各得0.5，故成员{3}新的联盟价值为0.5(=0+0.5)，而成员{1，2}新的联盟价值为5.5(=5+0.5).接下来，将5.5分配给{1，2}中的{1}和{2}，此时，{1，3}和{2，3}的幸福值之和为1.5(=6+0.5-5)为最小，因此平分其幸福值，各得0.75，各自新的联盟价值分别为3.75(=3+0.75)和2.75(=2+0.75)，在已知{3}的联盟价值为0.5的条件下，可得{1}和{2}新的联盟价值(分配值)分别为3.25(=3.75-0.5)和2.25(=2.75-0.5).由此，可求得该博弈的核仁为(y1，y2，y3)=(3.25，2.25，0.5)，进而可以求得三家公司各自的成本分摊分别为7.75(=11-3.25)，5.75(=8-2.25)和6.5(=7-0.5).

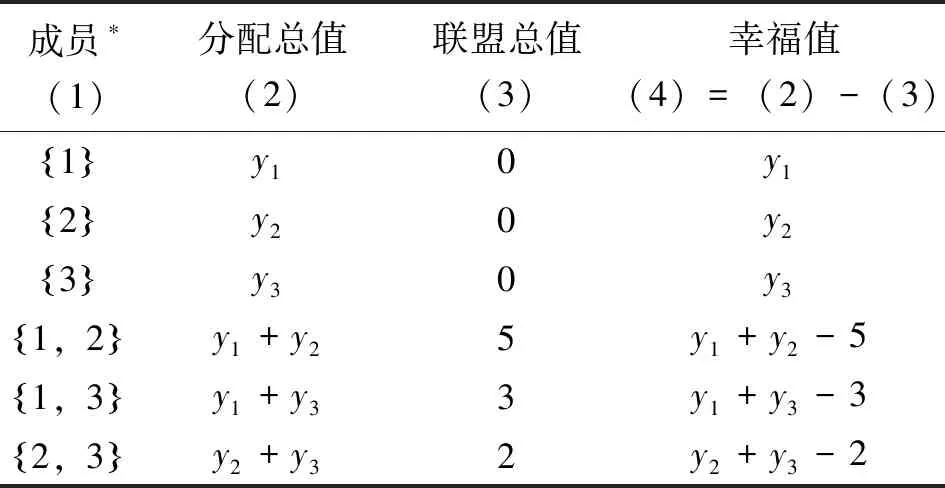
表2 各成员的幸福值

最后，求该博弈的夏普利值：参与人1、2、3共有六个排列，分别为：123，132，213，231，312，321.他们在这六个排列中的边际贡献分别为(0，5，1)，(0，3，3)，(5，0，1)，(4，0，2)，(3，3，0)，(4，2，0).因此参与人1、2、3的平均边际贡献(即夏普利值)分别为：8/3，13/6，7/6.如表3所示.进而，根据夏普利值的分配逻辑，三家公司各自分摊的成本分别为：25/3(=11-8/3)，35/6(=8-13/6)和35/6(=7-7/6).

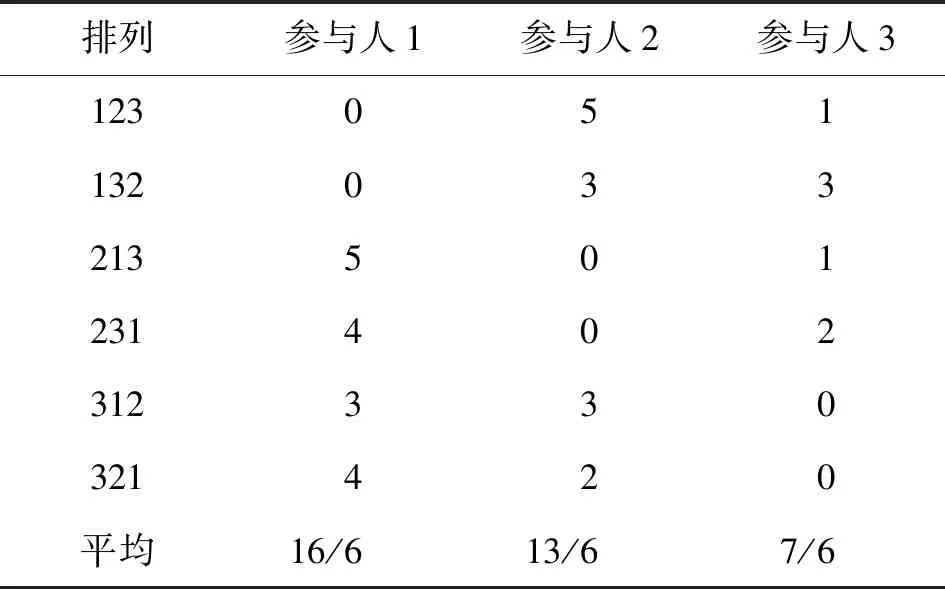
表3 博弈的夏普利值

4结语

目前，博弈论已形成一个相对完备的方法论体系，成为一种强有力的数理分析工具，并广泛应用于经济学、管理学、社会学、政治学等社会学科领域[11].由于其多使用复杂的数学方法构建博弈模型，又被称为社会科学的物理学.

博弈论有两个分支：非合作博弈与合作博弈.冯·诺伊曼和摩根斯坦首次提出合作博弈的概念，并对合作博弈进行了大量的讨论和研究，而他们对非合作博弈的研究仅介绍了简单的零和博弈，也就是说，博弈论最先发端于对合作博弈[12].继纳什之后，学者们对非合作博弈展开了深入细致的研究，取得了丰富的成果，使其成为体系相对完备的一个分支，而合作博弈的研究进展则相对滞后，始终落后于非合作博弈.

当前，在企业、社会、国家面临新的竞争与合作关系的背景下，合作博弈由于其侧重于合作效率以及公平分配的研究，更加符合新型竞合关系的内在要求[13]，因此，需要加强对合作博弈理论与应用的探索和研究，为促进企业、社会、国家之间的协调与合作作出应有的贡献.