基于符号回归的受弯破坏矩形RC剪力墙变形能力预测

马 高, 王 瑶

(1. 湖南大学 土木工程学院,湖南 长沙 410082; 2. 工程结构损伤诊断湖南省重点实验室(湖南大学), 湖南 长沙 410082)

0 引言

RC剪力墙作为一种常用的抗侧力构件,在现代高层结构中得到了广泛应用,现行规范大多基于承载力对剪力墙进行抗震设计。而WALLACE等[1]指出对于大多数剪力墙结构而言,这种设计方法并不经济。MEDHEKAR等[2]指出在基于承载力的设计方法中,仅在设计结束后对位移予以检查,缺乏对非弹性位移的关注。这可能导致剪力墙构件在较强的地震荷载下发生过大的变形,引起结构倒塌或导致结构的震后修复价值降低。针对基于承载力设计方法存在的缺陷,MEDHEKAR等[2]提出了基于位移的抗震设计理论。在基于位移的设计方法中,由于位移取代承载力成为设计过程中的控制目标,使得结构损伤得到控制,这一点在实际应用中得到了验证[3]。

对于基于位移的设计方法,构件变形能力的计算尤为重要。我国抗震规范[4]虽然对剪力墙变形限值做出了规定,但并未给出剪力墙变形能力的计算公式。国内外不少学者基于试验数据的回归拟合得到了剪力墙变形的经验或半经验公式:钱稼茹等[5]基于集中塑性铰模型与回归分析得出受弯破坏剪力墙的极限位移角经验公式;鲁懿虬等[6]在考虑剪切位移对受弯破坏剪力墙总位移贡献的基础上,利用119个受弯破坏剪力墙试验数据拟合了剪力墙极限位移计算公式;GRAMMATIKOU等[7]根据866个剪力墙试验数据验证并修正了BISKINIS等[8]基于回归分析提出的RC构件极限位移角经验公式。上述研究成果均是基于相关性分析和回归分析,且大多是根据一定理论分析将设计参数多项式组合后再进行线性回归。然而,由于线性回归的局限性与剪力墙变形机理的复杂性,即便根据一定理论基础将设计参数进行多项式组合,也很难完全分析出剪力墙极限位移与设计参数间的复杂关系。

这种机理复杂的非线性回归问题适合采用机器学习方法进行分析。NGUYEN等[9]利用神经网络建立了矮墙抗剪承载力预测模型,其精度高于现有的经验公式。MANGALATHU等[10]利用机器学习技术对梁柱节点的抗剪承载力进行了预测。虽然机器学习模型具有较高的精度,而模型本身可解释性较差是不能忽视的问题,造成设计人员难以从模型本身解释设计参数对结构性能的影响。在此背景下,特征重要性与SHAP(SHapley Additive exPlanations, SHAP)法作为解释工具开始获得关注,如MANGALATHU等[11]利用特征重要性对剪力墙破坏模式分类模型进行了解释;FENG等[12]根据SHAP量化评价了各个设计参数对剪力墙抗剪强度的影响。

虽然基于特征重要性和SHAP等解释工具,机器学习模型可解释性较差的问题得到了一定解决。但具有符号模型的经验公式格式紧凑、可解释性强,在制定设计规范与实际工程使用时具有很强的指导意义。KOZA[13]提出了基于符号回归(symbolic regression,SR)的机器学习技术用于建立符号模型,该方法能够在具备可解释性、高泛化性的前提下建立具有较高精度的非线性符号模型。DAVIDSON等[14]在符号回归的基础上引入最小二乘法,增强了算法在搜寻符号模型中常数项最优解的能力。由于现有的符号回归分析一般基于遗传算法,该算法在处理高维数据时无法进行针对性的特征数量放缩,导致符号回归在处理高维数据时效果不佳,往往会陷入局部最优。因此,本文运用SHAP进行特征选择,剔除不重要的特征参数以降低数据维度。

基于上述研究背景,本文基于符号回归方法建立了矩形RC剪力墙的极限位移计算公式。首先收集了119个弯曲破坏矩形RC剪力墙实验数据用以进行模型的训练与测试。然后,训练机器学习模型以计算各个特征参数的SHAP值,根据SHAP值进行特征选择。将筛选后的特征参数进行符号回归,建立了矩形RC剪力墙的极限位移计算公式,并与现有文献模型进行对比分析。

1 剪力墙数据库介绍

本文从文献[7,15-26]筛选了119个发生弯曲破坏的矩形RC剪力墙试验数据,所筛选的剪力墙均为矩形RC剪力墙,带暗柱构造,不包含腹板配置钢板、抗剪件、交叉斜筋等改进措施的RC剪力墙。

用于极限位移预测的特征参数为:墙高H、剪跨比λ、高厚比H/tw、轴压比n、墙体竖向分布筋配筋特征值ρwvfy,wv/fc、墙体水平分布筋配筋特征值ρwhfy,wh/fc、暗柱纵筋配筋特征值ρcvfy,cv/fc、暗柱箍筋配筋特征值ρchfy,ch/fc,各参数具体分布如图1所示。其中,n=P/(bhwfc),P为轴压力,b为墙体截面宽度,hw为墙体截面高度,fc为混凝土圆柱体抗压强度;ρwv为腹板竖向分布筋配筋率;ρwh为腹板水平分布筋配筋率;ρcv为暗柱纵筋配筋率;ρch为暗柱箍筋体积配筋率;fy,wv为腹板竖向分布筋屈服强度;fy,wh为腹板水平分布筋屈服强度;fy,cv为暗柱纵筋屈服强度;fy,ch为暗柱箍筋屈服强度;Δu为剪力墙承载力下降到峰值80%时的位移。

图1 参数分布直方图Fig. 1 Distribution histogram of parameters

2 机器学习预测结果与分析

2.1 模型的训练与结果

本文选用了支持向量机(surpport vector machine,SVM)[27]、决策树(decision tree,DT)[28]、神经网络(artificial neural network,ANN)[29]、随机森林(random forest,RF)[30]、XGBoost[31]等多种机器学习模型对矩形RC剪力墙的极限位移进行了回归预测。受篇幅所限,对所使用模型的算法原理不做赘述。

数据库中数据按7∶3的比例随机划分为训练集和测试集,训练集用于建立预测模型,测试集用于检验模型的预测性能。本文采用决定系数(R2)、均方根误差(root mean square error,RMSE)、平均绝对差(mean absolute error,MAE)、平均百分比误差(mean absolute percentage error,MAPE)衡量模型预测的准确性,各指标定义如下:

(1)

(2)

(3)

(4)

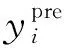
此外,在进行初步训练时,模型出现了不同程度的过拟合现象。对于过拟合,一般解决方法有:交叉验证[32]、正则化和增加训练数据[33]。由于目前公开的试验数据有限,本文首先主要考虑使用10折交叉验证来确定模型的超参数并限制模型的过拟合的现象,模型训练流程示意图如图2所示。经交叉验证之后,多数模型的过拟合现象得到了有效控制,但XGBoost的过拟合现象仍然存在,故对其进行了正则化处理并限制其采样率,有效降低了过拟合程度。

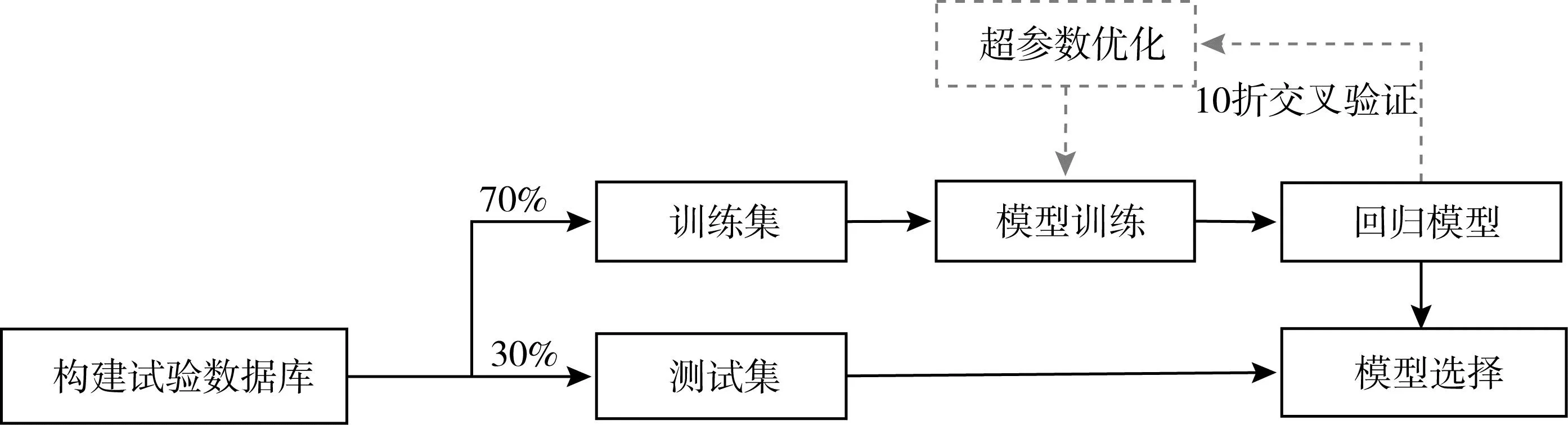
图2 模型训练流程示意图Fig. 2 Schematic diagram of model training

预测模型在训练集与测试集中的表现如图3与表1所示。从各模型的预测结果来看,XGBoost的预测效果最好,模型在训练集、测试集中均有较高的R2,RMSE、MAE和MAPE也处于较低的水平,预测值与试验值基本吻合,离散性较低;SVM、ANN、DT这几种基础模型的预测效果要弱于RF、XGBoost这种集成学习模型的预测效果。

表1 模型性能指标Table 1 Performance indexes of models

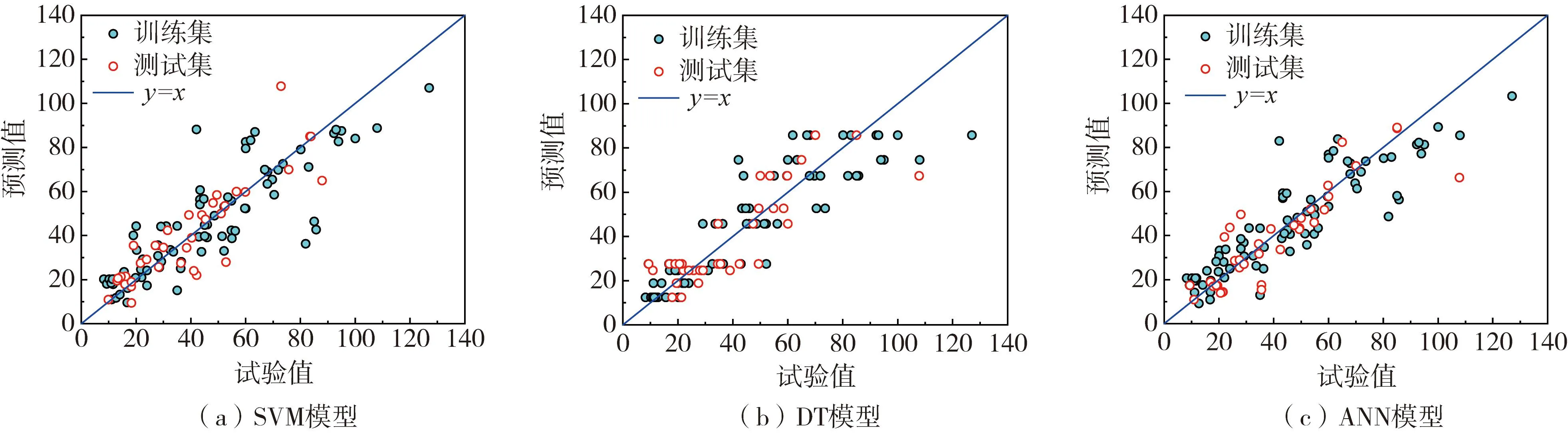
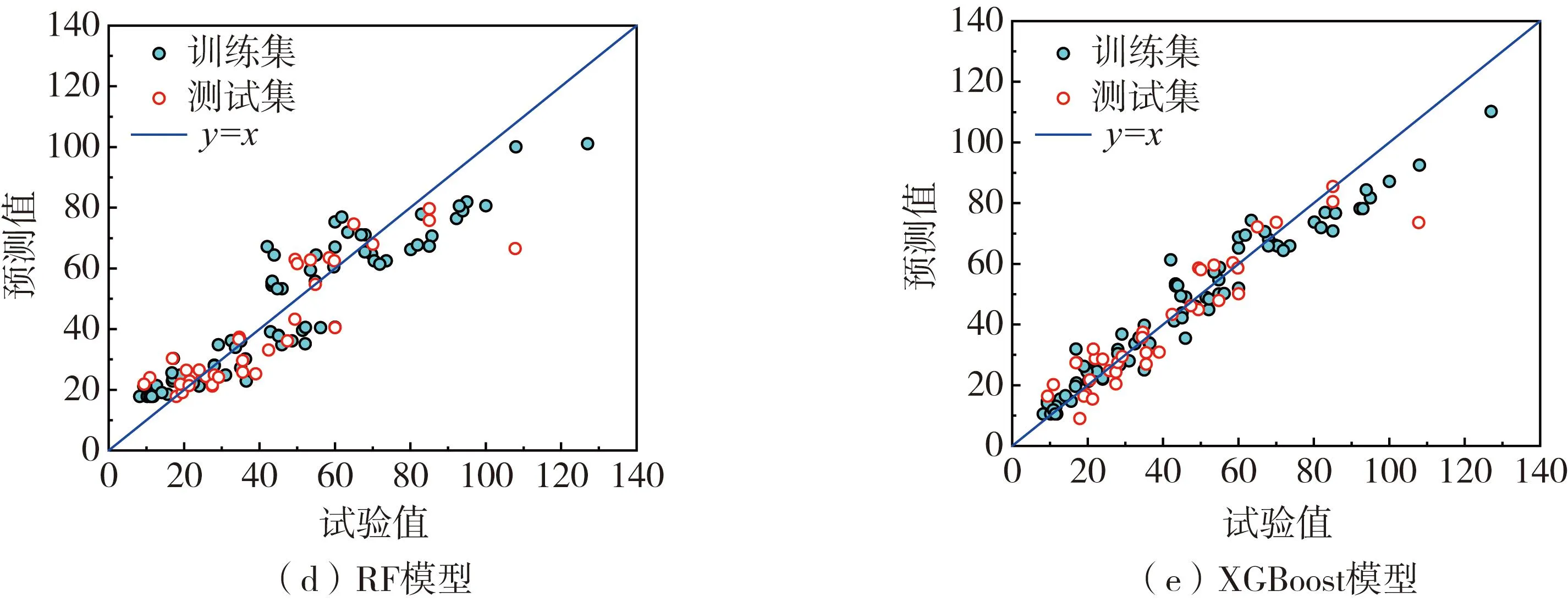
图3 模型预测结果Fig. 3 Prediction results of models

2.2 基于SHAP的模型解释与特征选择

本文采用LUNDBERG等[34]提出的SHAP方法进行模型解释。SHAP基于博弈论建立了一套计算各个特征参数Shapley值的方法,以量化各个特征参数在模型中的重要性。此外,SHAP还可以分析各个特征参数对单个样本的影响。本文应用SHAP对2.1节中预测效果最好的XGBoost模型进行了相应分析,其结果如图4所示。

图4 XGBoost模型SHAP分析结果Fig. 4 Analysis results of XGBoost model with SHAP analysis results

根据SHAP分析结果可得出如下结论:

1)由图4(a)可知,弯曲破坏矩形RC剪力墙极限位移的主要影响参数为:墙高H(mm)、剪跨比λ、轴压比n、暗柱纵筋配筋特征值ρcvfy,cv/fc、暗柱箍筋配筋特征值ρchhfy,ch/fc。而高厚比H/tw、墙体竖向分布筋配筋特征值ρwvfy,wv/fc、墙体水平分布筋配筋特征值ρwhfy,wh/fc影响较小。

2)暗柱纵筋配筋特征值ρcvfy,cv/fc与暗柱箍筋配筋特征值ρchfy,ch/fc越高,其SHAP值越高,对剪力墙极限位移有积极影响。考虑到弯曲破坏剪力墙破坏特征一般表现为受压区混凝土压溃或纵筋拉断,这是由于暗柱配箍的增加能加强对暗柱混凝土的约束,暗柱纵筋配筋的增加能延缓暗柱纵筋的拉断。

3)墙体竖向分布筋配筋特征值ρwvfy,wv/fc、墙体水平分布筋配筋特征值ρwhfy,wh/fc的SHAP值较低,腹板分布筋对于弯曲破坏剪力墙的变形能力影响较小。结合弯曲破坏剪力墙的破坏形态,破坏区域一般集中在暗柱区与塑性铰区。这说明对于弯曲破坏剪力墙,加强腹板分布筋配筋率并不能有效提高其变形能力。

4)轴压比n越高,其SHAP值越低,其对剪力墙极限位移有不利影响。这是因为随着轴压比n的增加,截面受压区高度也随之增加,导致剪力墙变形能力下降。剪跨比λ越高,其SHAP值越高,其对剪力墙极限位移有积极影响。

根据SHAP分析结果,用于符号回归的特征参数为:墙高H(mm)、剪跨比λ、轴压比n、暗柱纵筋配筋特征值ρcvfy,cv/fc、暗柱箍筋配筋特征值ρchfy,ch/fc。

3 符号回归分析

3.1 方法简介

符号回归是由KOZA[13]提出的一种基于遗传算法的回归方法,用于建立参数间的符号模型,同时尽可能减小误差指标。DAVIDSON等[35]在KOZA[13]的基础上引入了最小二乘法,以增强算法搜索符号模型中常数项的能力。其中,符号模型是指字母与运算符表示的函数表达式。符号回归不同于常见的回归方法,其并不需要预先设定回归公式的形式,而是通过遗传算法的选择、交叉、变异等步骤,以建立回归模型。本文选取RMSE作为适应度函数的评价标准,适应度函数表现最佳的公式树将进行交叉、变异组成新的子代,其过程包括:①随机生成初始表达式,建立初始种群;②基于适应度函数表现选择部分表达式进行交叉、变异,创造新的子代种群;③当迭代至设定代数时,终止程序,输出适应度函数最优的表达式。程序中的交叉、变异过程示意图如图5所示。

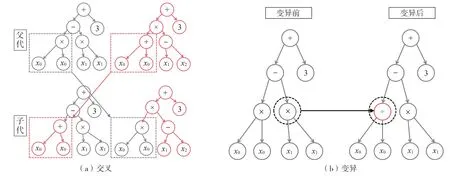
图5 程序内部交叉、变异操作示意图Fig. 5 Schematic diagram of internal crossover and mutation operation of the program

3.2 训练过程与结果分析

将2.2节中筛选过后的特征参数用于符号回归。与2.1节类似,将数据集按7∶3的比例划分为训练集与测试集,将训练集与测试集上的模型性能表现进行对比以验证其泛化能力与可靠性。在选择最终的最优表达式时,主要考量如下因素:①性能指标,即R2、RMSE、MAE、MAPE;②公式复杂程度,一般以公式树的长度衡量;③量纲平衡。基于上述原则,本文得到的剪力墙极限位移计算公式为:

(5)

其在训练集与测试集上的表现如图6与表2所示。从符号回归模型的形式来看,其满足量纲平衡原则,公式形式也较为简洁。模型在训练集、测试集、整体数据集上均有较高的R2,且其R2与RMSE评价指标均比较接近,证明其泛化性能较好。

图6 符号回归模型预测结果Fig. 6 Prediction results of symbolic regression model表2 符号回归模型性能指标Table 2 Performance indexes of symbolic regression model数据集R2RMSEMAEMAPE训练集0.7114.2210.8437.88测试集0.7213.149.7828.46整体数据集0.7213.810.5135.02

3.3 参数分析

为直观分析各特征参数在符号回归模型中对剪力墙极限位移的影响,本文对其进行参数分析。对某个参数进行参数分析时,其余特征参数取其在数据集中的平均值。同时,为对比符号模型与一般机器学习模型间的差异,将本文3.1节的XGBoost模型参数分析结果与符号回归模型进行对比。

由图7可知,在符号回归模型与XGBoost模型中,各个参数对剪力墙极限位移的影响趋势比较接近。墙高H、剪跨比λ、暗柱纵筋配筋特征值ρcvfy,cv/fc、暗柱箍筋配筋特征值ρchfy,ch/fc对剪力墙极限位移有积极影响,轴压比n对对剪力墙极限位移有负面影响,分析结论与2.2节SHAP分析结果基本一致。然而符号回归模型与XGBoost模型在部分参数的部分区间上存在较大差异,例如对于墙高H两者在[0,900]区间差异较大。从评价指标上看,XGBoost模型精度高于符号回归模型,但从实际物理意义角度考量,XGBoost模型结果没有符号回归模型合乎实际。因为在其他参数不变的情况下,Δu应随着H的减小而减小,且当H趋近于0时Δu也应趋近于0。结合数据库中参数分布分析,这可能是因为数据集中H的范围为[900,4572],导致XGBoost模型在[0,900]区间上的精度不足。这也验证了符号回归模型的泛化性能要比XGBoost模型高,可解释性更强。

3.4 与现有模型的性能对比

为验证符号回归模型的预测能力,本文选用已有文献中较为典型的计算模型进行对比分析。

1)钱稼茹等[5]模型

(6)

式中:θu为极限位移角;ξ为截面相对受压区高度;λ剪跨比。

2)鲁懿虬等[6]模型

(7)

εcu=260ρε1+ε0.85

(8)

ε1=εc0[1+5(fcc/fc0-1)]

(9)

lp=0.2hw+0.044Hw

(10)

(11)

式中:η为轴压比系数,当0≤n≤0.1时,η=1;当n>0.1时,η=5n2+0.95;ξ为截面相对受压区高度;λ为剪跨比;εcu为约束混凝土极限压应变;ρ=∑Asc/[s(bcx+bcy)],Asc为约束区箍筋2个方向的总面积;s为箍筋间距;bcx、bcy分别为箍筋约束区2个方向的长度;ε1为约束混凝土峰值应变,εc0取0.002;fcc为约束混凝土峰值应力;fc0为普通混凝土峰值应力;lp为塑性铰长度;hw为截面高度即剪力墙宽度;Hw为墙高;Δs为剪力墙剪切位移;Δf为剪力墙弯曲位移;εm为截面中部应变;φ为剪力墙底部曲率可由平截面假定计算。

3)GRAMMATIKOU等[7]模型

(12)

(13)

(14)

式中:ast取0.0158,aw,r取5/8,aw,nr取1;w为受拉钢筋配筋特征值与腹板纵筋配筋特征值之和;w′为受压钢筋配筋特征值;ρd为斜筋配筋率;a为约束区有效因子;sh为箍筋间距;bo、ho为约束区2个方向的长度;bi为约束区纵筋间距。

4)WALLACE等[36]模型

(15)

5)ACI 318-19[37]规范

(16)

式中:c为受压区高度;l为剪力墙宽度。

6)ALLOUZI等[38]模型

(17)

(18)

式中:λ为剪跨比;Vmax为抗剪承载力;Kw为剪力墙初始刚度;Kfl为抗弯刚度;Ksh为抗剪刚度。

7)DEGER等[39]模型

(19)

式中:ρcv为暗柱纵筋配筋率,单位为%;bo为暗柱厚度;tw为腹板厚度。

表3与图8为式(5)与各经验公式在本文测试集上的对比结果。其中Δu_exp为剪力墙极限位移的试验值;Δu_pre为剪力墙极限位移的预测值;Cv为Δu_exp/Δu_pre的变异系数。从对比结果来看,本文提出的模型具有更高的精度,(Δu_exp/Δu_pre)mean接近1,且离散性较低,变异系数为0.32。用于比较的经验模型R2均小于本文模型,预测效果较差。

表3 符号回归模型与各经验公式间的预测性能对比Table 3 Comparison of prediction performance between symbolic regression model and empirical formulas

图8 各模型计算值与试验值对比Fig. 8 Comparison between calculated values and test values of each model

在文献模型中,ALLOUZI等[38]模型具有最高的R2,(Δu_exp/Δu_pre)mean为1.23,计算结果较为保守,变异系数较大(Cv=0.42)。DEGER等[39]模型预测效果最差,(Δu_exp/Δu_pre)mean为0.51,计算结果显著偏大。被欧洲规范采用的GRAMMATIKOU等[7]模型预测效果较美国规范ACI 318-19规范[37]更好,ACI 318-19规范[37]计算结果偏于保守。

4 结论

基于已有的试验数据,建立了一个含有119个弯曲破坏矩形RC剪力墙的试验数据库,提出了基于符号回归预测弯曲破坏矩形RC剪力墙变形能力的方法。该方法首先基于数据库训练多个机器学习模型,通过SHAP法对机器学习模型进行解释与分析,并基于SHAP值对特征参数进行筛选。基于筛选后的特征参数进行符号回归分析,提出了弯曲破坏矩形RC剪力墙极限位移计算公式。主要结论如下:

1)弯曲破坏矩形RC剪力墙的极限位移主要由以下参数控制:墙高H、剪跨比λ、轴压比n、暗柱纵筋配筋特征值ρcvfy,cv/fc、暗柱箍筋配筋特征值ρchfy,ch/fc。高厚比H/tw、墙体竖向分布筋配筋特征值ρwvfy,wv/fc、墙体水平分布筋配筋特征值ρwhfy,wh/fc对极限位移的影响较小。

2)符号回归模型与XGBoost模型中,各个参数对剪力墙极限位移的影响趋势比较接近。但由于所使用数据集区间限制,XGBoost在[0,900]区间内的预测结果与实际情况不符,而符号回归模型在此区间的预测结果更合乎实际,符号回归模型较XGBoost模型具有更好的泛化性能。

3)与已有的经验模型对比,本文提出的符号回归模型具有最佳的预测精度与最低的离散程度。这是因为已有的经验模型大多利用线性回归结合一定力学模型的方法建立模型,对非线性关系预测效果较差,而符号回归模型对非线性关系具有更强的预测效果。