一类计算机病毒传播模型的动力学性态研究
党耀宇,谭宏武,曹 慧
(陕西科技大学 数学与数据科学学院,陕西 西安 710021)
0 引言
随着信息网络的快速发展,计算机病毒在网络中的传播已成为一种常见现象,而计算机感染病毒后,会不同程度地影响人们的工作和生活,甚至会造成巨大的经济损失.因此,了解计算机病毒的传播动力学性态也许能为抵御病毒的攻击提供一些防御技术的设计思路.
由于计算机病毒感染的过程与流行病学感染过程类似[1],因此已有不少学者基于经典的传染病仓室模型建立了动力学模型来研究计算机病毒的传播[2-7],包括SIS模型[2-3]、SIR模型[4-5]、SIRS模型[6]、SVEIR模型[7].由于计算机病毒的隐秘性,导致计算机感染病毒后需要经历一段时间后才能被防御系统识别并清除.
本文基于经典的SIRS传染病仓室模型,将网络中的计算机分为未感染类、感染类和恢复类,并分别用S(t)和R(t)表示t时刻未感染类计算机和恢复类计算机的数量,I(t,a)表示t时刻感染年龄为a的感染类计算机的密度.该模型中感染年龄a指的是病毒在感染仓室中所停留的时间长度,并不是实际的年龄,而是一种类年龄结构.计算机病毒传播过程如图1所示.
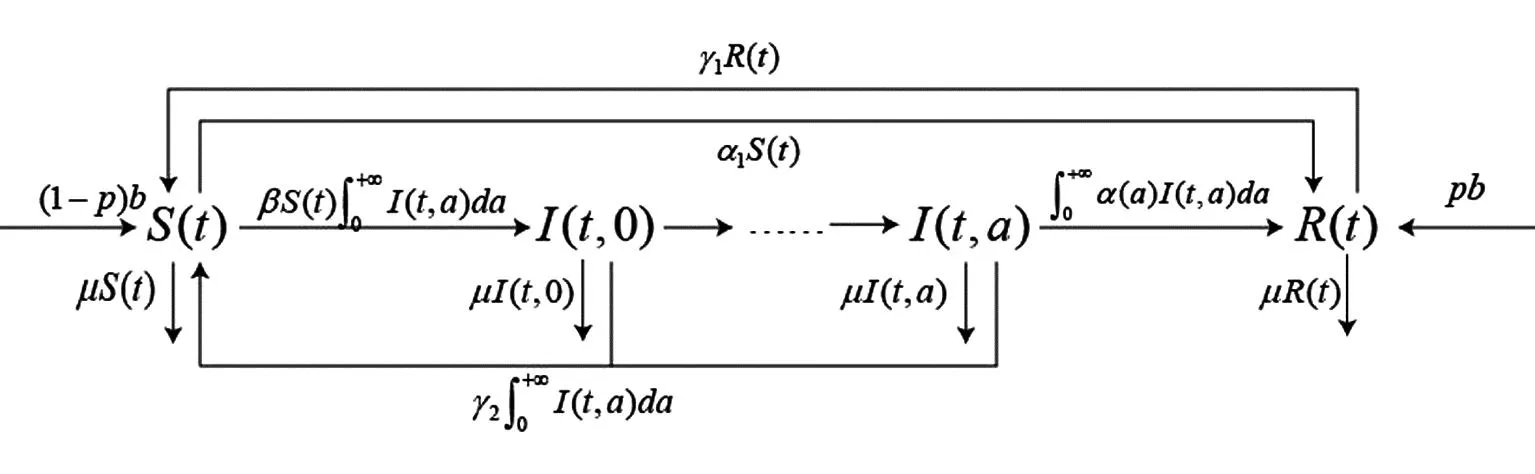
图1 基于SIRS模型的计算机病毒感染进展流程图
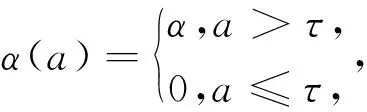

(2)
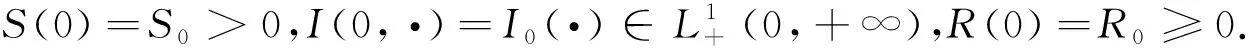
(3)
1 适定性
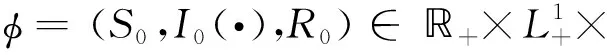

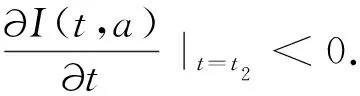
(4)


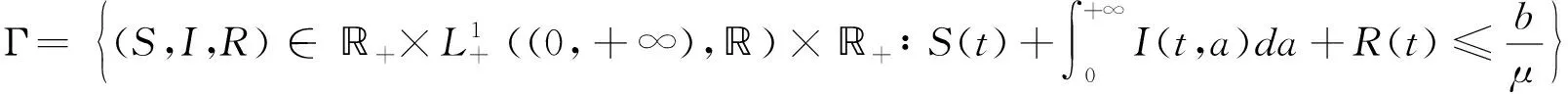
2 平衡态的存在性
为了得到系统(1)的平衡态,需要求解以下方程组(5).
下面先讨论系统(1)的无病毒平衡态.
当I(a)=0时,直接求解可得系统(1)始终存在无病毒平衡态E0=(S0,0,R0),其中,
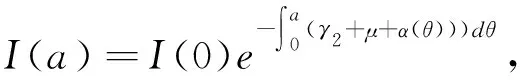
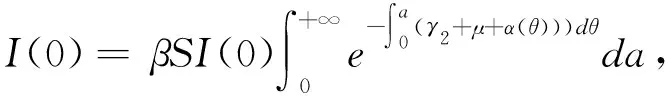

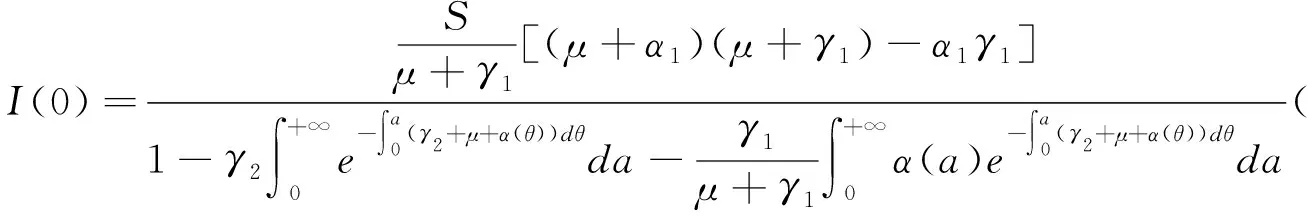
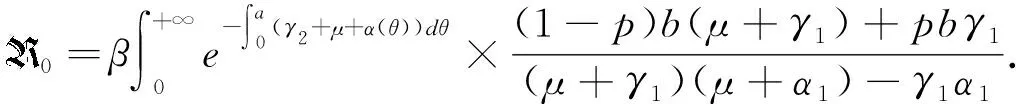
(6)

(7)

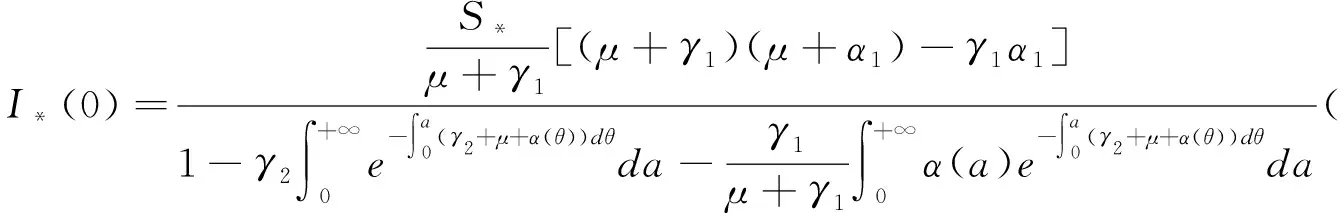

3 平衡态的稳定性
3.1 无病毒平衡态的稳定性

证明将系统(1)在E0处线性化,得到的特征方程为:
(8)
其中,2μ+α1+γ1>0,μ(μ+γ1+α1)>0,由劳斯-赫尔维茨判据可知Δ(λ)=0的两个根的实部都小于0.当λ∈时,是关于λ的连续严格单调递减的实值函数,且满足0-1.因此,当0>1时,Δ2(λ)=0至少有一个正实根,即无病毒平衡态E0是不稳定的.

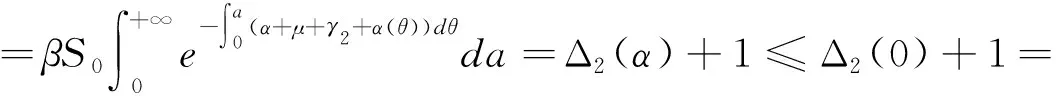


引理3.2[9]设g∶+→是一个有界函数,
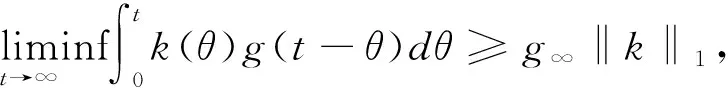

证明为了建立无病毒平衡态E0的全局渐近稳定性,设(S(t),I(t,a),R(t))是系统(1)的解,由系统(1)的第二个方程与边界条件(2)得到
(9)
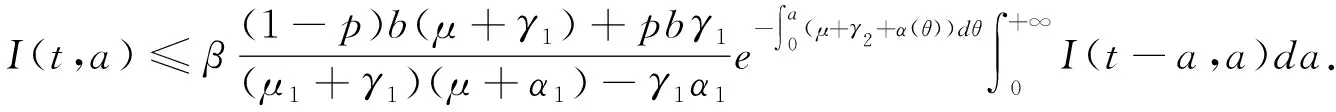
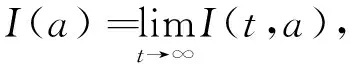
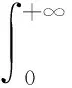
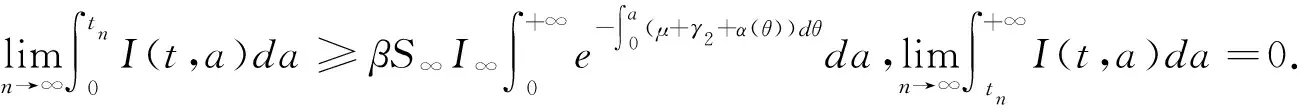
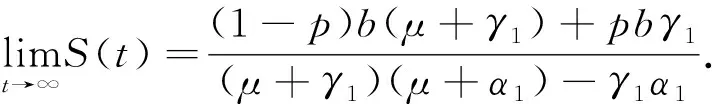
3.2 病毒平衡态的稳定性
f(λ,τ)=λ3+A2(τ)λ2+A1(τ)λ+A0(τ)+B0(τ)e-λτ=0,
(11)
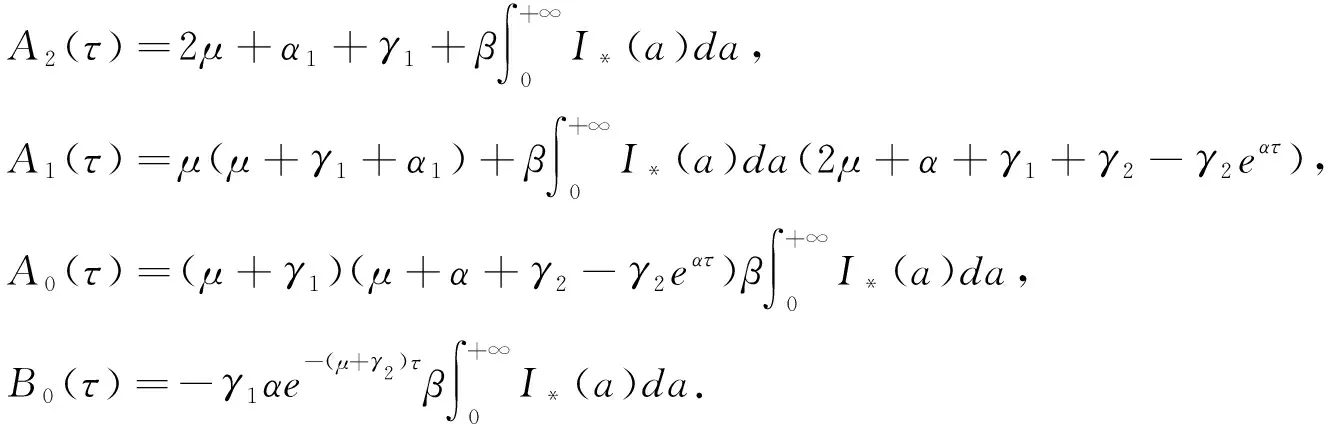
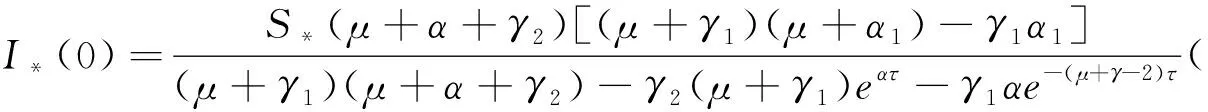

证明通过直接计算,可得

A1(0)A2(0)-(A0(0)+B0(0))
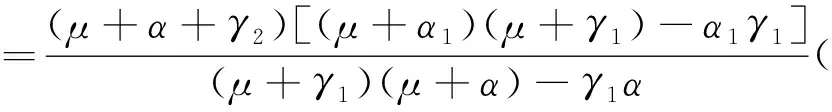
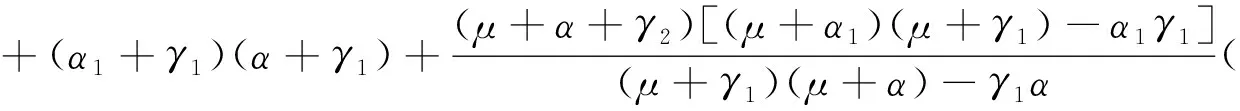
+μ(2μ+γ1+α1)(μ+γ1+α1)>0.

4 Hopf分支
当τ>0时,将特征方程f(λ,τ)=0改写为超越方程
P(λ,τ)+Q(λ,τ)e-λτ=0
(12)
其中:P(λ,τ)=λ3+A2(τ)λ2+A1(τ)λ+A0(τ),Q(λ,τ)=B0(τ).
根据参考文献[10]的第二节,需要证明如下假设:
(Ⅰ)P(0,τ)+Q(0,τ)≠0;
(Ⅱ)P(iω,τ)+Q(iω,τ)≠0;
(Ⅳ)F(iω,τ)=|P(iω,τ)|2-|Q(iω,τ)|2;
(Ⅴ)当F(iω,τ)=0存在正根ω(τ)时,其在τ中是连续且可微的.
通过计算,可得:


则满足上述条件(Ⅰ)、(Ⅱ)、(Ⅲ).
注意到,因为
所以
(13)
则条件(Ⅳ)成立.由于F(ω,τ)是关于ω2的三次多项,且Ai(τ)(τ=1,2,3)和B0(τ)都是关于τ的连续可微函数,因此条件(Ⅴ)也成立.
令λ=iω(ω>0)是f(λ,τ)=0的一个纯虚根,则
-iω3-A2(τ)ω2+A1(τ)iω+A0(τ)+B0(τ)(cosωτ-isinωτ)=0.
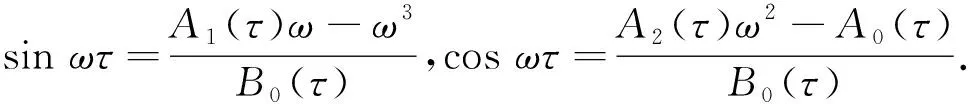
Q(Θ)∶=Θ3+q2(τ)Θ2+q1(τ)Θ+q0(τ)
(14)
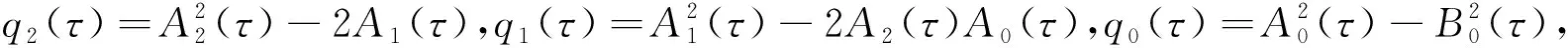
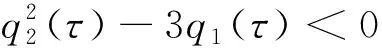
引理4.1
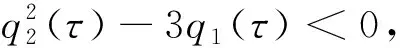
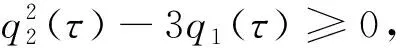
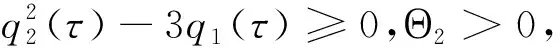
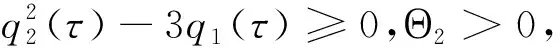
若式(14)没有正根,则随着τ的增加,病毒平衡态E*的稳定性并没有发生变化.反之,若式(14)存在正根,当τ达到某个临界值τ*时,病毒平衡态E*的稳定性可能会发生变化.综上所述,可以得到如下结论:

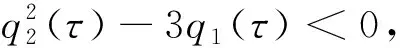
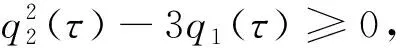
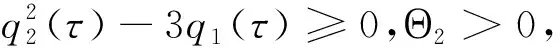
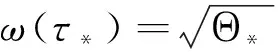
对τ∈Σ,则存在ω=ω(τ)>0,使得F(ω,τ)=0.
令θ(τ)∈(0,2π](τ∈Σ)是以下方程的解:
有ω(τ)τ=θ(τ)+2nπ,因此ω*=ω(τ*)是(11)的纯虚根,当且仅当对于n∈有τ*是Cn的零点,.
从参考文献[10]中定理2.2可得到以下引理:
引理4.2假设ω(τ)是τ∈Σ定义的F(ω,τ)=0的正实根,在τ*∈Σ时,
Cn(τ*)=0,n∈.
则在特征方程(11)中τ=τ*存在一对共轭纯虚根,λ+(τ*)=iω(τ*),λ-(τ*)=-iω(τ*),并且
当δ(τ*)>0时,虚根从左到右穿过虚轴.反之,当δ(τ*)<0时,虚根从右到左穿过虚轴.
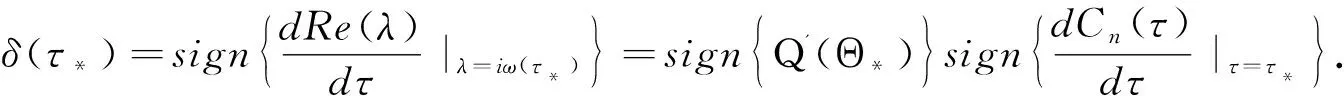
当Q'(Θ*)≠0且τ=τ*时发生了Hopf分支,根据Hopf分支定理得到如下结论:

5 数值模拟和结论
本文提出了一个具有年龄结构和时滞的获得性免疫的计算机病毒模型,并将年龄结构和时滞结合起来描述,当感染的计算机停留在感染类一段时间后,由于获得性免疫而成为恢复类计算机的病毒传播现象.与传统的计算机病毒模型相比,不仅考虑了病毒的感染时长,还考虑了不同感染情况下的治愈能力,因此本文考虑的模型更为现实.同时,本文也对病毒在计算机系统中出现的Hopf分支情况进行了理论分析和数值模拟.另一方面,本文的目的是分析讨论感染年龄和病毒感染的时滞对病毒传播的影响.

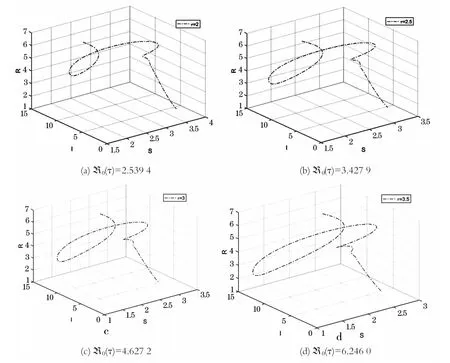
图2 病毒平衡态E*在τ不同取值情况下的稳定性
讨论时滞在τ>0的情况下,感染年龄a对于模型的影响.图3(a)表明,在图2病毒平衡态渐近稳定的情况下,此时病毒平衡态处的感染个体I*(a)会随着感染年龄的不断增大而逐渐减少,直至为0.这说明此时计算机病毒的传播是可以得到有效控制的.图3(b)表明,对于整个模型而言,感染年龄a和感染时间t同时增大时,感染个体I(t,a)会不断减少.然而,在数值模拟中发现,当时滞超过某个临界值τ*时,系统会出现Hopf分支,这意味着计算机病毒流行的状态从感染平衡状态变为极限环.也就是说,计算机病毒的传播已经失去了控制.图4说明系统经历了Hopf分支,此时Hopf分支范围内时滞τ的取值很小.然而,当时滞超过临界值后,系统的稳定性会再次发生变化成为渐近稳定的.
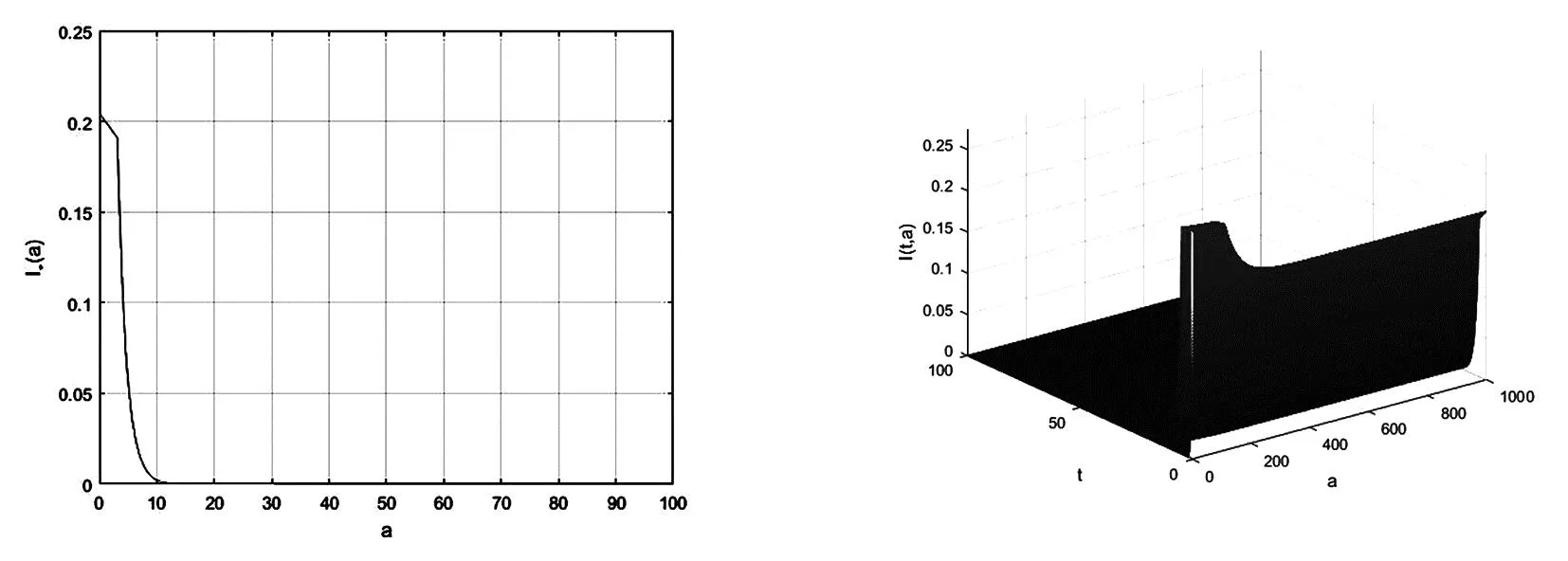
(a) I*(a)在E*处的分布 (b) I(t,a)的分布
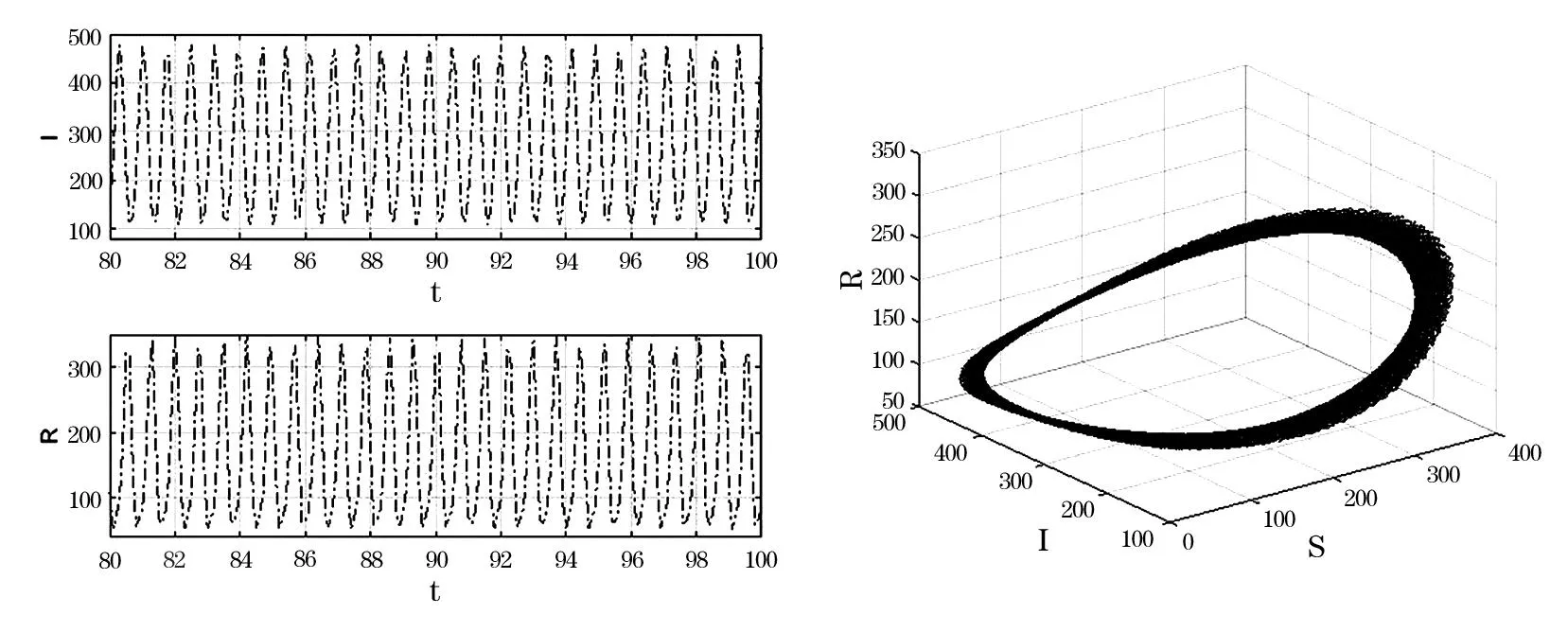
(a) 周期解 (b) 相图


