基于表面肌电信号的手势识别方法

崔冰艳, 邓嘉, 张祥

(华北理工大学机械工程学院, 唐山 063210)

脑卒中通称中风,是一种脑部缺血或出血性损伤导致的疾病。80%～90%的脑卒中患者会存在不同程度的手部运动功能障碍症,脑卒中患者腕部功能障碍主要表现为腕部僵硬,腕自由度的缺失[1]。根据临床调研发现,患者的主动康复训练更有助于康复[2],因此基于上肢康复训练系统的自主康复训练研究具有广阔前景。

康复训练是通过恢复激活肌肉的机能来达到康复目的,表面肌电信号(surface electromyography,sEMG)的成功运用在很大程度上取决于特征提取和选择。到目前为止的研究中,没有确定哪些类型的特征可以充分表达sEMG数学特性。目前,sEMG特征提取方法主要包括时域、频域、时频域和非线性动力学分析[3-4]。sEMG的分类方法主要有支持向量机(support vector machine,SVM )、反向传播神经网络(back propagation neural net-work,BPNN)、随机森林(random fores,RF),K最近邻算法(K-nearest neighbor,KNN)、线性判别分析(linear discriminant analysis,LDA)和深度学习 (deep learning,DL)[5]。

实现上肢运动动作的识别是机电控制的关键。张龙娇等[6]提出一种融合卷积神经网络(convolutional neural network, CNN)和长短时记忆网络(long short term memory, LSTM),将手势控制臂环采集到的8通道sEMG数据进行分类,实验的结果表明手势识别准确率为91.6%。刘光达等[7]提出改进的果蝇优化算法基础上把遗传算法的交叉变异和果蝇优化算法混合,并与神经网络结合对肌肉疲劳进行识别,准确率为94.3%,优于其他方法。来全宝等[8]以提高手势识别的准确率,提出一种人工鱼群算法优化的极限学习机(artificial fish swarm algorithm-extreme learning machine, AFSA-ELM)分类模型,实验结果表明,结合最优特征组合与最优滑动窗口设计的AFSA-ELM分类模型对多种手势的平均识别准确率高达97.4%,比BPNN分类模型和未优化的ELM分类模型分别高3.5%和1.6%。吴田等[9]提出基于sEMG和混合算法优化支持向量机(particle swarm optimization-genetic algorithm-support vector machines,PSO-GA-SVM) 的舒适度评估方法,引入基于希尔伯特黄变换(Hilbert-Huang transform,HHT) 的平均瞬时功率(averaged instantaneous frequency,AIF) 作为特征参数,构建了基于混合算法优化支持向量机的评估模型,模型的准确率为 93.5%,可有效量化评估绝缘杆类工器具的舒适度。Qureshi等[10]针对手势识别,提出了CNN和预训练转移学习(transfer learning,TL)模型之间的比较,该模型实现了更高的精度和更低的计算成本。结果表明,CNN可以显著提高模式识别sEMG控制方案的有效性。Qin等[11]提出了一种基于通道卷积神经网络模型(channel wise-convolutional neural network, CW-CNN)的sEMG信号虚拟手控实时控制系统,并在两天内对8名健康实验人员进行了三次实验。实验结果表明,该系统在3自由度运动回归中具有较高的精度,系统稳定,计算延迟低。Xing等[12]使用具有卷集成层的五个并行架构的 CNN 模型对 Ninapro DB2 数据库进行分类和测试。实验结果表明,CNN方法的分类准确率为83.23%,高于SVM和RF方法。Hu等[13]提出了一种基于注意力的混合CNN和RNN(CNN-RNN)架构,NinaProDB1、NinaProDB2、BioPatRec子数据库、CapgMyo子数据库和csl-hdemg数据库的识别准确率分别为87.0%、82.2%、94.1%、99.7%和94.5%,比现有技术性能分别提高了9.2%、3.5%、1.2%、0.2%和5.2%。Vijayvargiya等[14]提出了一种混合小波与集合经验模态分解预处理技术的方法,称为WD-EEMD(wavelet decomposition-ensemble empirical mode decomposition),用于下肢活动进行分类。Pradhan等[15]在sEMG信号研究中,提出三个特征提取方法,时域特征、时频域特征和自回归特征,并在通道数1～8不等的情况下研究它们的组合。其中,对于识别系统,四通道配置的平均误差对于时域特征为3%,对于时频域特征为12.4%,对于自回归特征为36.3%。

综上所述,很明显,深度学习方法可以在sEMG手势识别中实现更好的分类性能,使用CNN对sEMG信号进行分类的准确性普遍高于传统分类方法。许多研究表明,时域和时频域特征提取对sEMG信号分类具有识别性,并且多特征融合的sEMG信号更具识别度。在国内外研究中上肢运动识别的研究中准确率还有待提高。因此,为了提高上肢手势动作的识别准确率,基于sEMG信号对上肢手势动作识别进行了研究。首先进行sEMG信号的预处理,包括了信号去噪和数据分割。其次进行sEMG信号的特征提取,将时域和时频域特征相融合,采用积分肌电值、均方根值和小波包变换系数构造为特征空间IEME和RMSME。最后使用SVM、AFSA-SVM 和CNN对特征空间进行了分类结果对比。

1 sEMG信号采集与处理

1.1 实验设计

在表面肌电信号采集实验过程中使用的设备为Delysis TrignoTM无线肌电仪,如图1所示,它具有16路无线传感器,可同时采集16块肌肉的肌电信号和3轴加速度。

根据局部解剖学原理,手臂的屈伸运动主要由上臂肌肉区控制,握拳和伸肌主要由前臂肌肉群控制[16]。根据本文实验的动作,选择指浅屈肌与指伸肌作为表面肌电信号的来源,如图2所示。

图1 Delysis TrignoTMFig.1 Delysis TrignoTM

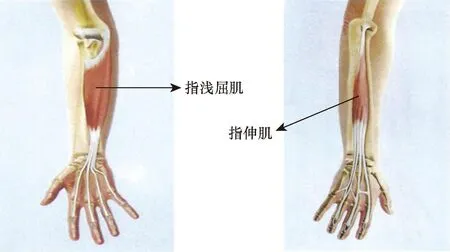
图2 指浅屈肌与指伸肌位置示意图Fig.2 Location of flexor digitorum superficialis and extensor digi-torum

实验共采集了10位年龄为25+2岁的受试者,其中包括了8位男性和2位女性。在整个实验过程中,受试者被要求以足够稳定的方式进行,以消除姿势差异引起的干扰。受试者使用右手进行见表1的手势动作完成sEMG信号采集。为了排除肌肉疲劳对表面肌电信号的影响,受试者在任何两个动作之间休息2～5 s。实验期间,受试者以2～5 s的运动周期完成了至少6次同一上肢运动,一共完成三组实验。

1.2 sEMG去噪

sEMG是幅值仅为μV级的微电信号,它具有非线性与非平稳特点。sEMG分布在500 Hz以下的频带范围内,其中主要频率集中在10～300 Hz,核心能量集中在20～150 Hz[17]。基于sEMG信号的特点,可知它极易受到噪声的干扰,因此在使用sEMG信号之前必须滤除其中的噪声。考虑巴特沃斯滤波器比切比雪夫滤波器具有更平滑的滤波特性,所以选用巴特沃斯滤波器去噪。使用巴特沃斯滤波器对sEMG信号进行截止频率为10 Hz的高通滤波去除低频噪声,截止频率为300 Hz的低通滤波去除高频噪声。使用巴特沃斯滤波器从一阶到五阶对原始的sEMG信号进行去噪,通过信噪比(signal-noise ratio, SNR)大小进行选择,结果见表2。

SNR值越大,说明去噪效果越好,所以由表2可知,在三阶时对sEMG信号的去噪效果最好,因此本文选择三阶巴特沃斯滤波器进行信号去噪,对1号受试者的1号动作去噪处理如图3所示。

表1 八种手势运动Table 1 8 gesture movements

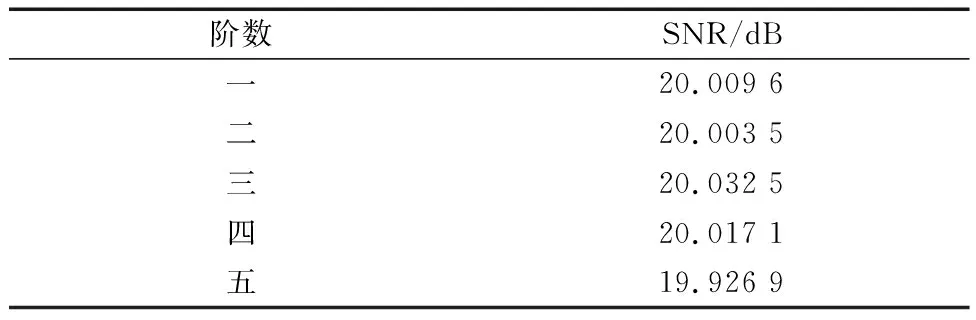
表2 不同阶数的信噪比值Table 2 Signal to noise ratio of different orders

图3 三阶巴特沃斯滤波器去噪Fig.3 Third order Butterworth filter denoising

1.3 时间滑动窗口数据分割

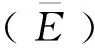
(1)分段样本数:分段样本数是指使用时间滑动窗口后生成的数据段数,表达式为

(1)

式(1)中:L表示数据量。

按照正常完成一个动作流程时间一般为2～6 s,采用2 000 Hz的采样频率,所以单个动作数据量。因此计算可得N=12～1 495。实验的采样频率为2 000 Hz,采样周期为0.5 ms,当Wd=8,该段数据的处理时间为4 ms,且数据量较大,使特征提取和分类器处理的时间加大,并对计算机性能的要求很高,还会限制算法的复杂性,数据量过少会导致分类模型过拟合。因此选择Wd为16、32和64。 对数据量的影响较小,但过大的W,会使信号的细节特征被吞没,所以选择W为32、64和128。因此W与Wd不同组合的数据量大小如表3所示。

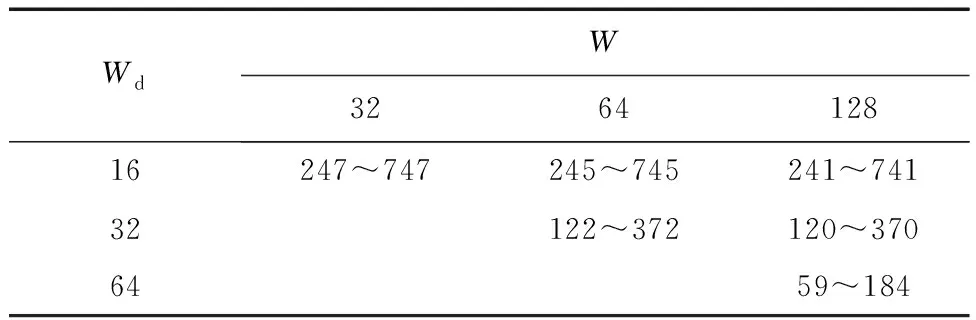
表3 W与Wd不同组合分段样本数Table 3 Number of segmented samples in different combinations of W and Wd

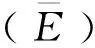
(2)

则滑动能量均值计算公式为

(3)

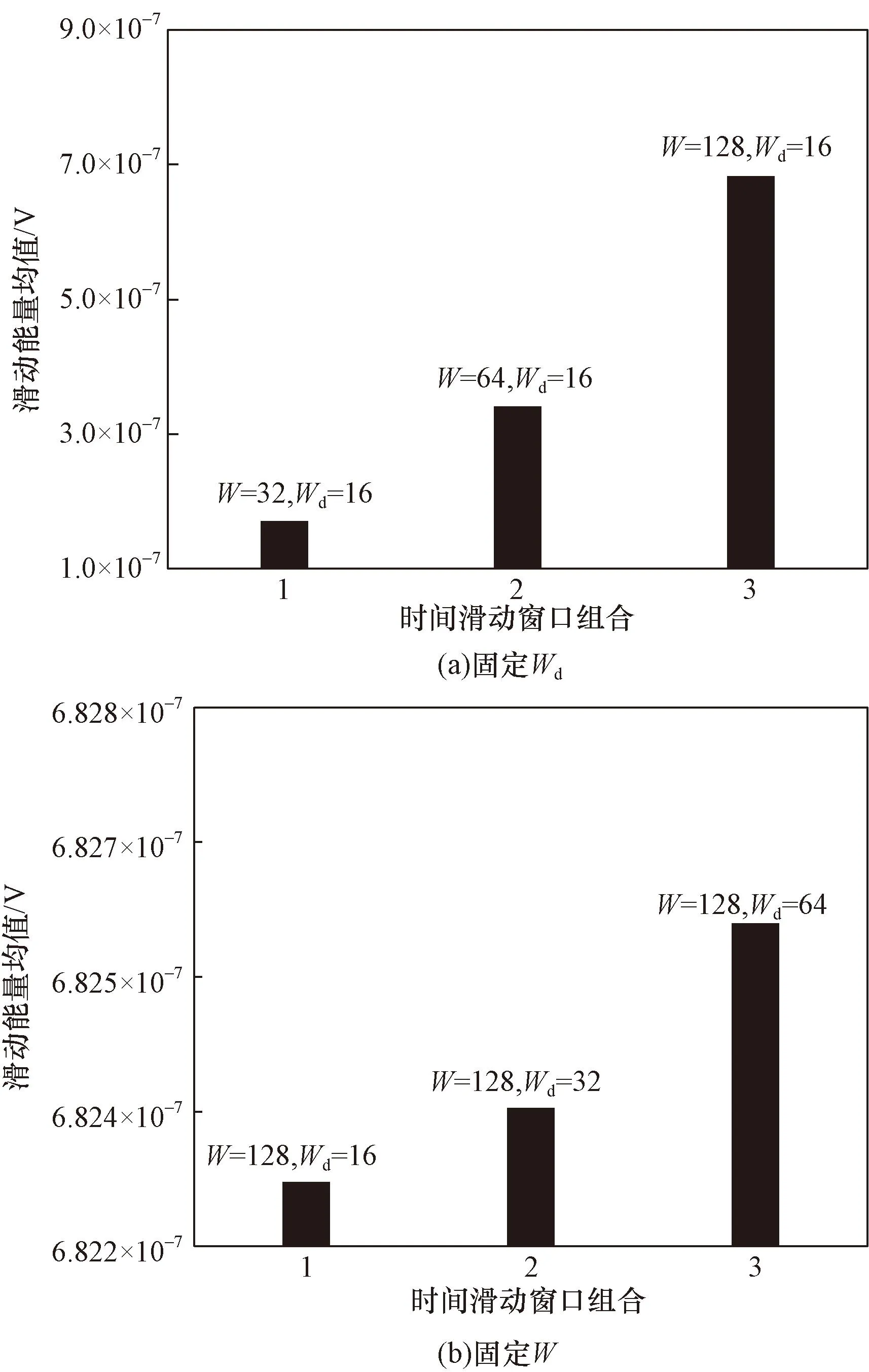
图4 滑动能量均值Fig.4 Mean sliding energy

1.4 特征提取

目前,表面肌电信号特征计算方法主要包括时域、频域、时频域和非线性动力学分析。为增强数据特征的可靠性,选用时域信号中的积分肌电值(integrated electromyography, iEMG)和均方根值(root mean square, RMS),时频域信号中的小波包变换(wavelet packet transform, WPT)作为特征提取。

1.4.1 积分肌电值

积分肌电值表示肌纤维的电荷活动程度[21],所有整流曲线下面积,能够体现肌电值的波动和能量熵。积分肌电值计算公式为

(4)

式(4)中:Z为信号数;Δt为信号点之间的时间差;xi为信号值。

以手掌伸展的肌电信号为例,其积分肌电值处理结果如图5所示。

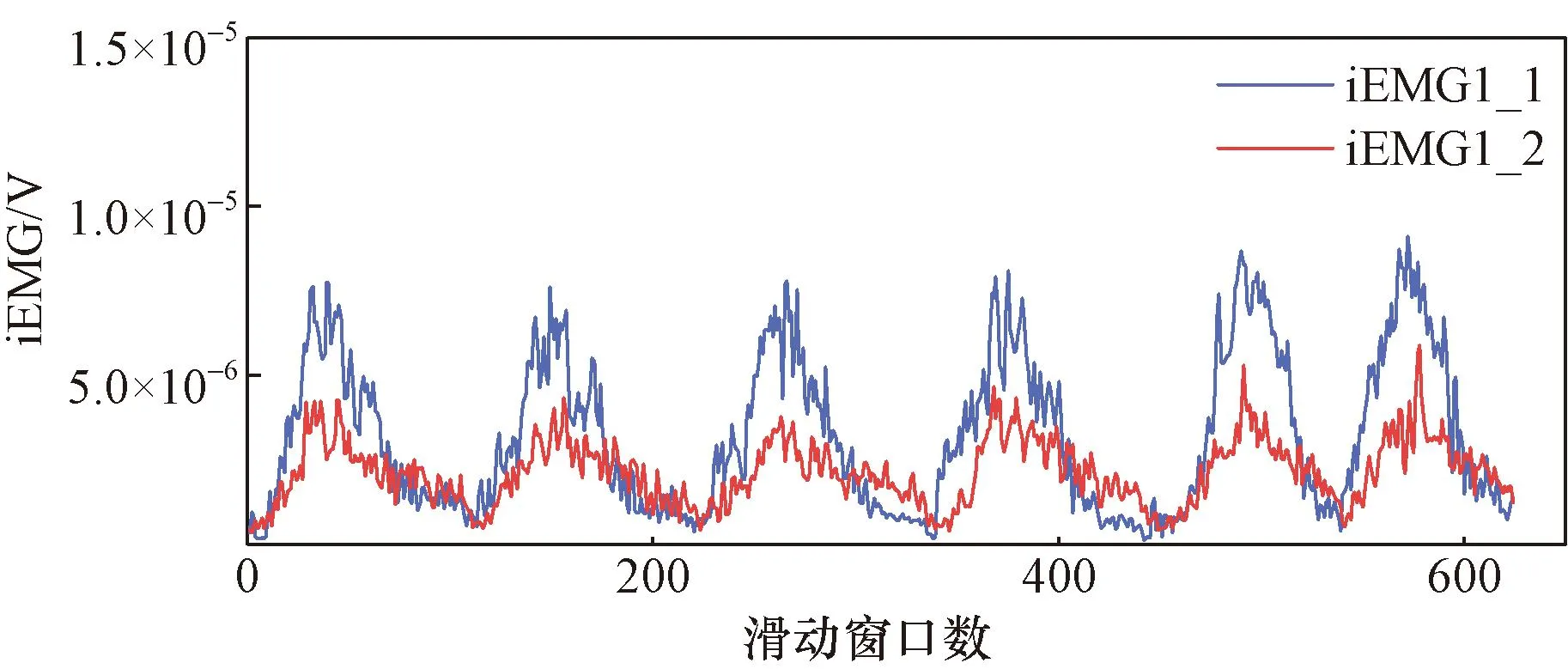
iEMG1_1表示1号动作手掌伸展的1号肌电传感器肌电积分值, iEMG1_2表示1号动作手掌伸展的2号肌电传感器肌电积分值图5 积分肌电值Fig.5 Integrated electromyography

1.4.2 均方根值

均方根值与肌电信号的能量直接联系[22],它表示表面肌电信号在单位时间内的变化,可以反映肌肉的活跃程度。均方根值计算公式为

(5)

式(5)中:M表示信号总数;xi为信号值。

采用与肌电积分值相同的动作与肌肉采集位置进行均方根值信号处理,结果如图6所示。

RMS1_1表示1号动作手掌伸展的1号肌电传感器均方根值; RMS1_2表示1号动作手掌伸展的2号肌电传感器均方根值图6 均方根值Fig.6 Root mean square

1.4.3 小波包变换

小波分析和小波包变换适合对非平稳信号的瞬态和时变特性分析,具有多尺度分析能力和良好的时频局部化特性[23]。

小波包变换满足双尺度方程,即

(6)

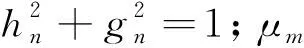
小波包变换包括小波包分解和小波包重构。

(1)小波包分解:对肌电信号进行j层小波包分解,得到2j个不同信号的子频带,并按低频到高频的顺序重新排列,采用正交小波包变换对信号x(t)进行分解,则l层k点的小波包分解系数,其公式为

(7)

(8)

式中:l为小波分解层数;r=0,1,2,…,2l-1为相应层数下节点的个数;k=1,2,3,…,2l为第j层的第k个节点。

(2)小波包重构:对小波包分解系数进行单支重构公式为

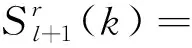
(9)

则总重构信号计算公式为

(10)

采用小波包变换中小波包系数最大值(max wavelet packet coefficient,MWPC)和小波包系数能量(energy wavelet packet coefficient,EWPC)作为特征提取。

小波包系数最大值计算公式为

MWPCi=lg(max|Si|)

(11)

式(11)中:Si表示对应频段的小波包系数。

小波包系数能量计算公式为

EWPCi=lg(ewpci)

(12)

式(12)中:Si表示对应频段的小波包系数;Mi表示不同频段。

将小波包系数最大值和小波包系数能量值进行融合,构建特征向量ME公式为

ME=[MWPCi,EWPCi]

(13)

式(13)中:i为对应的最后一层小波包分解个数。

以1号受试者的8种手势,每种6组数据为例,其处理结果如图7所示。

由图7可知,各动作的小波包系数具有明显区分度。

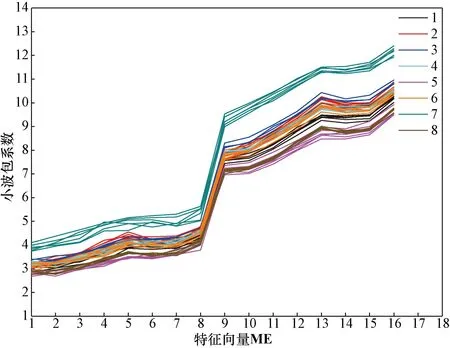
图7 特征向量MEFig.7 Feature vector ME

1.5 sEMG特征空间构造

将特征提取的多种信号联合构造为特征空间,更有利于表现信号的信息,增强动作间信号的区分性[24-25]。适量增加传感器通道数可增强数据的差异性,提高识别率。因此,分别构造积分肌电值和均方根值与小波包变换系数的特征空间。特征空间构造表达式为

IEME=[iEMG1ME1iEMG2ME2]

(14)

RMSME=[RMS1ME1RMS2ME2]

(15)

式中:iEMG1、ME1和RMS1为采集设备通道1的数值;iEMG2、ME2和RMS2为采集设备通道2的数值。

2 sEMG信号手势识别算法

2.1 人工鱼群算法

人工鱼群算法原理是模拟鱼的觅食、聚群和追尾行为,通过鱼群中每个个体的局部寻优,循序渐进从而得到全局最优值[26],该算法流程图如图8所示。

2.2 卷积神经网络

CNN主要包含输入层、卷积层、池化层、全连接层和输出层5个模块,其工作结构如图9所示。为了提高信息的深度和识别的准确率,通常多次使用卷积层、池化层和全连接层。

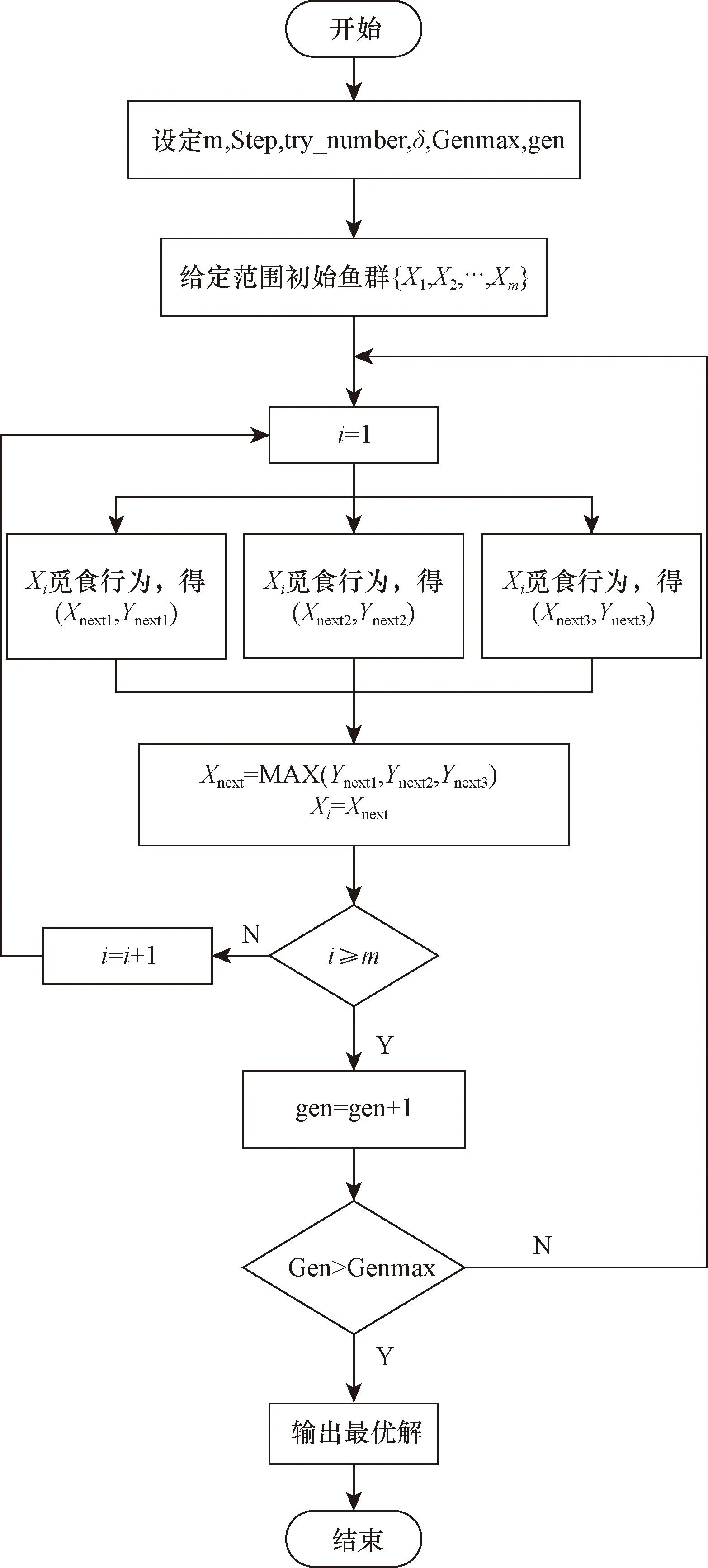
图8 人工鱼群算法流程图Fig.8 Flow chart of artificial fish swarm algorithm

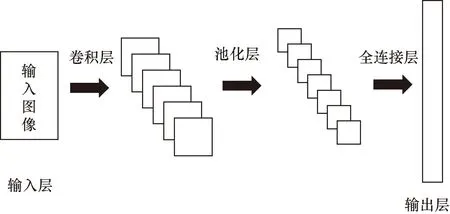
图9 CNN工作流程图Fig.9 CNN workflow diagram

在CNN中,输入层输入通过处理后的sEMG信号,将sEMG信号构建为图像信息,卷积层再进行局部特征提取后,池化层再进行下采样操作,通过特征选择和信息过滤将最有用的特征信息保存,全连接层对提取的特征进行非线性组合后得到输出,输出层为分类结果。

2.3 支持向量机

SVM的多分类是在二分类的基础上发展来,通过核函数和松弛变量将样本映射到高维空间,超平面间将空间划分为多个区域进行分类[27]。

本研究选择高斯核作为核函数,其公式为

(16)

式(16)中:σ核函数参数影响着样本映射到高维空间后的分布。

3 实验环境与结果分析

3.1 实验环境

实验的硬件环境:CPU为Intel i5-11260H频率2.6 GHz;GPU为NVIDIA GeForce GTX3050 Ti显存6GB。实验的软件环境:EMG works Analysis;MatlabR2020b;PyCharm2021;tesorflow2.0.0;keras2.3.1。

3.2 实验评估

采用交叉验证方法来证明所识别分类模型的实际识别率,随机选取70%的样本作为训练集,30%的样本作为测试集,将每一受试者的10次识别模型结果的平均值作为评估结果。

本文除了实验采集的数据,还采用了非侵入自适应假肢肌电2号数据集(non-invasive adaptive pros-thetics database 2,Nina Pro DB2),该数据集为可用于科学研究的公开数据集。Nina Pro DB2使用了与本文实验相同的肌电采集设备Delysis TrignoTM,采样频率皆为2 000 Hz。本文中选取了其中对应的动作运动类型和sEMG信号采集位置进行实验对比。

3.3 实验结果分析

利用AFSA对SVM径向基核函数(radial basis function, RBF)参数(c,σ)寻优,设人工鱼的数量m=100,最大迭代数Genmax=10次,最多试探次数try_number=10,感知距离gen=1;拥挤度因子delta=0.618; 移动步长step=0.1;当寻优次数达到所设的最大迭代数时,寻优终止并输出最优的(c,σ),其寻优迭代过程如图10所示。

对NinaPro DB2数据集中10位受试者的8种手势识别准确率如图11所示。

对实验采集10位受试者的8种手势平均识别准确率如图12所示。

由图11和图12可知,AF-IEME在整体的识别中具有明显优势,但在Nina Pro DB2数据集中手势4与手势6的识别率较低,在实验数据中手势5与手势8的识别率较低。

使用一维卷积神经网络(1D-CNN)和二维卷积神经网络(2D-CNN)对实验采集的10位受试者进行手势识别, CNN模型参数Batch_Size=16,epoch=50,其迭代过程如图13所示。

图10 AFSA-SVM迭代过程Fig.10 AFSA-SVM iterative process

使用精确率(precision)、召回率(recall)、F-measure值(F1)和平均训练时间对1D-CNN和2D-CNN测试集进行性能评价,其结果见表4。

由表4可知,1D-CNN相对于2D-CNN在精确率、召回率和F1上分别提升了3.9%、4.7%和4.29%。因此,1D-CNN作为识别模型具有优越性。

不同识别方法对实验采集的10位受试者的平均准确率(accuracy)如图14所示。

由图14可知,1D-CNN在实验采集的数据中具有良好的性能,准确率高达到了98.61%,相对于SVM和AFSA-SVM识别准确率提高了6.77%和10.61%,并且1D-CNN正负误差率较小,更加稳定。

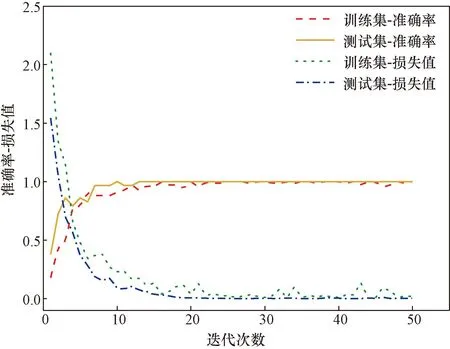
图13 CNN迭代过程Fig.13 CNN iterative process

表4 1D-CNN与2D-CNN评价结果Table 4 1D-CNN and 2D-CNN evaluation results

图14 手势识别平均准确率Fig.14 Average accuracy of gesture recognition

不同识别方法对实验采集的10位受试者平均训练时间见表5。

由表5可知,1D-CNN平均训练用时最少,相对于SVM和AFSA-SVM训练速度提高68.32 s和221.53 s,用时最高的AFSA-SVM虽然提高了准确度,但是其寻优耗时较长。因此,1D-CNN在三种识别方法中不论是分类准确度和训练时间均具有明显优越性。

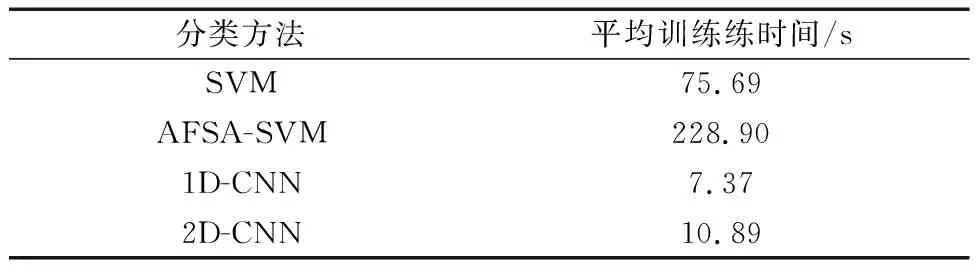
表5 平均训练时间Table 5 Average training time

4 结论

本文提出了结合时域与时频域特征的sEMG信号特征空间构造方法,提出了基于sEMG信号的SVM分类器、AFSA优化的SVM分类器和深度学习CNN分类模型,对上肢手势动作进行了识别分类对比。首先对实验采集的sEMG信号进行了去噪以及时间滑动窗口预处理,然后进行了积分肌电、均方根值和小波包变换特征提取,在特征提取基础上构造了特征空间IEME和RMSME。实验结果表明,不论在实验采集的数据中和Nina Pro DB2公开数据集中,特征空间IEME的识别准确率总体高于特征空间RMSME的识别准确率。在IEME中运用1D-CNN模型具有最高识别准确率98.61%,相对于SVM和AFSA-SVM识别准确率提高了6.77%和10.61%,并且1D-CNN模型平均训练时间相对于SVM和AFSA-SVM减少了68.32 s和221.53 s。因此,将1D-CNN运用在特征空间IEME的手势识别中具有一定优越性。深度学习模型在基于表面肌电的动作识别分类上相对传统分类方法具有一定优势,并且多特征的信号融合使动作更具区分度。在未来的工作中致力于将该模型运用在动态检测中,为上肢康复机器人控制提供新的交互方式。