考虑群井效应下的预降水引发地表沉降计算与分析

陈卫兵, 李彦, 魏焕卫, 王基文, 尚文涛*

(1.山东电力工程咨询院有限公司, 济南 250013; 2. 山东建筑大学土木工程学院, 济南 250101; 3. 山东建筑大学建筑结构加固改造与地下空间工程教育部重点实验室, 济南 250101; 4. 山东建筑大学地铁保护研究所, 济南 250101)

随着中国社会经济迅速发展,地下空间开发需求越来越大,深基坑向着更深、更大方向发展。深基坑往往建立在潜水层,在地下水位较高的地方,为确保基坑开挖干作业,通常先用降水井进行预降水处理再进行基坑开挖。降水会形成降落漏斗,在降落漏斗范围内会发生如地面沉降、塌陷等环境效应[1-2],对于周边距离较近的建筑,过大的地表沉降将造成地面建筑物的倾斜,甚至开裂破坏[3-5]。所以,对于距基坑较近的建筑,需要提前考虑降水对周围地表沉降值的影响。

基于稳定流的理论方法计算降水引起地表沉降值已有较多的研究。施成华等[6]和姚文龙等[7]考虑水的渗流作用,采用随机介质理论推导了基坑降水引起地表沉降计算公式,并用实际工程验证所提方法的可行性。吴意谦等[8]引入非饱和土体有效应力原理,在忽略群井效应的前提下推导了考虑渗流力作用的疏干土和饱和土的竖向沉降量计算公式,通过数值模拟和工程实例进行了对比分析。江杰等[9]、原华等[10]和张志红等[11]研究了止水帷幕对地表沉降的约束作用,探讨了降水过程中止水帷幕对地表沉降的影响范围。李琳等[12]和王晓华等[13]对比了不同水位降深的地表沉降,揭示了降水引起地表沉降的空间分布规律。胡长明等[14]针对黄土地区降水引起地表不均匀沉降问题,引入修正系数,推导出降水引起地面沉降的简化计算公式。杨清源等[15]通过模型试验,揭示了不完整井有效影响深度和基坑外土层孔隙水压变化规律。上述研究降水引起地表沉降的方法主要基于单井的稳定流理论,考虑群井效应方面的研究较少,存在一定的局限性。数值模拟方法有精度高、应用广的优点,在工程实例中,为更快得到计算结果,降低计算成本,往往采用直接划定干区域的计算方法[16-20],对于考虑群井效应下渗流过程的研究较少。

现考虑群井效应,基于理论计算和数值模拟两种方法,研究分析群井降水对地表沉降的影响。理论计算方面,基于裘布衣假设和稳定流的理论,推导出预测水位降深曲线,提出用该曲线和原地下水线为分界,将沉降范围内土层划分为干土区、疏干区和饱和区,疏干区采用规范法计算附加应力,饱和区考虑渗流力作用下的附加应力,用分层总和法分别计算三个区域的沉降值,叠加得最终沉降值;数值模拟方面,采用PLAXIS 3D中井单元模拟群井,用流固耦合对预降水期间周围地表沉降求解,通过井单元流量计算和降水前后孔压分析,揭示群井效应下抽水流量规律,展示预降水孔压变化过程。最后结合规范法和工程实测数据进行对比分析,结果表明理论计算方法和数值模拟结果合理可行,可以较好地应用于实际工程。

1 群井降水引起地表沉降计算

1.1 降水引起地表沉降机理

降水引发地表沉降机理可以用有效应力原理[21]解释。对于受降水影响的区域,原地下水位下的饱和土的总应力值为土的有效应力和孔隙水压力之和,表达式为

σ=σ′+γwh′

(1)

式(1)中:σ′为有效应力,kPa;σ为总应力,kPa;γw为水的重度,kN/m3;h′为原地下水位至计算点的垂直高度,m。

在降水后的疏干区,假设降水前后总应力不变,降水后土体中孔隙水压力减小,土的有效应力逐渐增大,土体的有效应力增量即为降水引起的附加应力。降水后的饱和区处于稳定流状态,在总应力不变的假设下,存在水头差引起的渗流力作用的附加应力,附加应力的产生会对土骨架有压缩作用,宏观上表现为土体产生竖向位移,即产生竖向沉降[8]。

1.2 群井降落漏斗浸润线方程

如图1所示,为便于计算,用裘布衣假设条件[22],忽略降水过程中竖向渗流速度,将降水过程中的等水头面近似为铅垂面,再根据渗流连续性条件,各铅垂面的流量相等,就可以用分离变量法和叠加法求解群井降水作用下的浸润线方程[23],即

(2)

式(2)中:y为在计算点处以隔水底板为边界浸润线高度,m;h0为井中水位,m;q1,q2,…,qn为单井抽水流量,m3/d;x1,x2,…,xn为计算点距离井轴的水平位置,m;r1,r2,…,rn为各井井半径;k为土层渗透系数。

为进一步简化计算,可假设各抽水井完全相同且抽水能力也相同,则可得

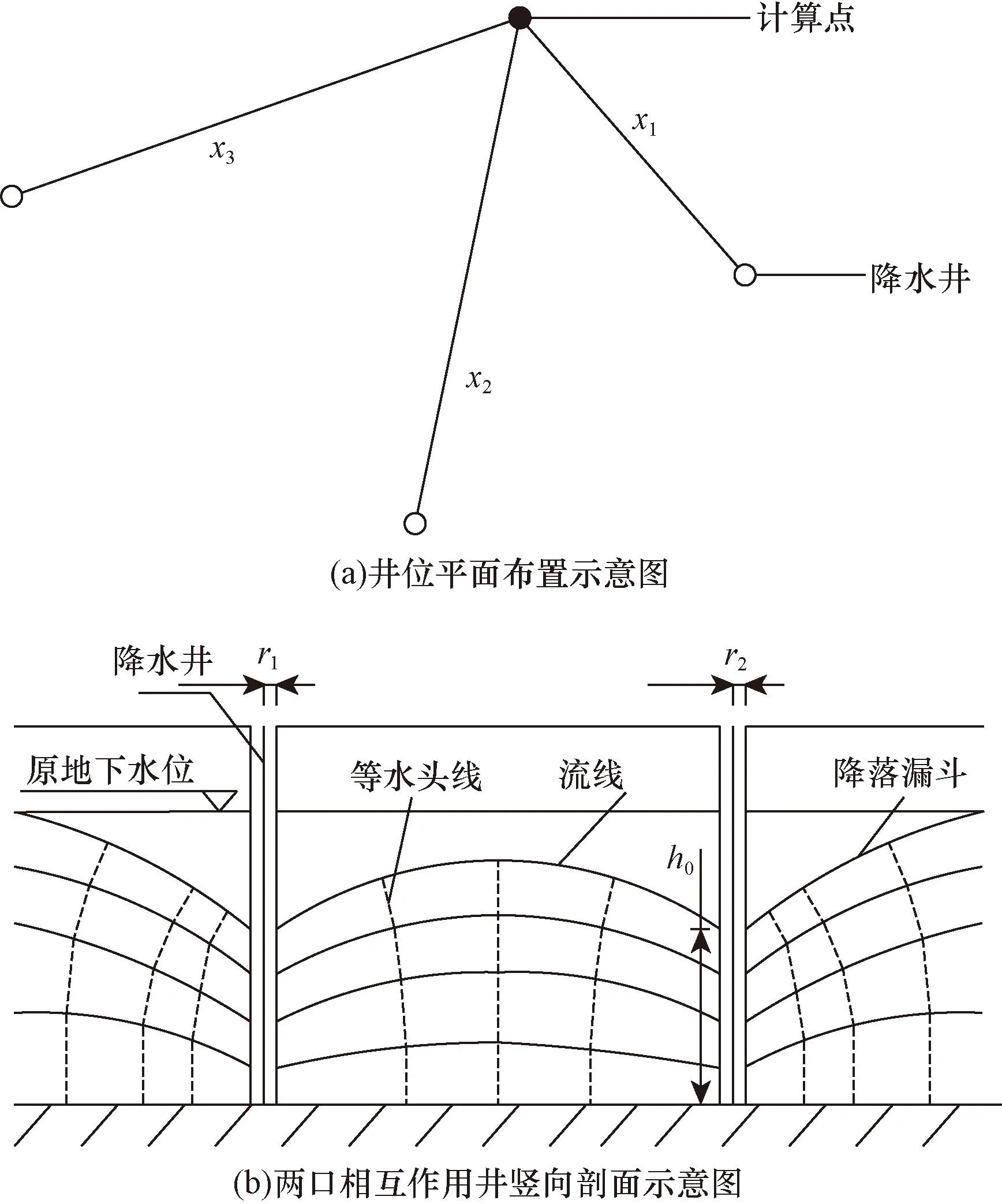
图1 群井作用示意图Fig.1 Schematic diagram of group well action

(3)

式(3)中:q为假设所有井完全相同的抽水流量,m3/d;n为抽水井个数。

1.3 预测水位降深曲线

规范法在计算各点水位降深时,在渗透系数k确定的情况下,采用流量设计值q来求解群井浸润线方程。但在实际工程中抽水量q往往达不到该设计值,此时,计算点处水位降深值大于实际降深值,用分层总和法计算的沉降值也是保守的。考虑群井效应,在群井降落漏斗浸润线方程上做出改进。如图2所示,以不透水层顶面为x轴,过计算点做铅垂线为y轴建立直角坐标系。

由基坑预降水设计水位和计算点水位可得群井浸润线公式为

(4)

式中:y1为以隔水底板为边界预降水设计水位高度,m;a1,a2,…,an为基坑预降水设计水位点距各井井轴水平距离,m。

联立式(3)和式(4)解y值,得预测水位降深曲线表达式为

(5)

式(5)中:a1,a2,…,an为基坑预降水设计水位点距各井井轴距离,m;x1,x2,…,x3为计算点距各井井轴距离,m。

图2 两口互相作用井降水示意图Fig.2 Schematic diagram of dewatering in two interaction wells

1.4 考虑渗流力作用的沉降计算

在降水引起的沉降范围内以原地下水位线和预测水位降深曲线为分界划分为干土区S1、疏干区S2和饱和区S3,如图3所示。对于干土区S1,其基本不受降水影响,表现为该区域的附加应力为0,所以沉降值s1也为0;对于疏干区,降水对该区域有疏干作用,其沉降值可用规范法[24]进行计算;对于饱和区,在形成稳定流的状态下,形成水头差H-y(H为潜水层厚度),饱和区内一直存在着渗流力γw(H-y),其方向与水平方向夹角为α,渗流力的竖向分量Δσy即为产生竖向沉降的附加应力。

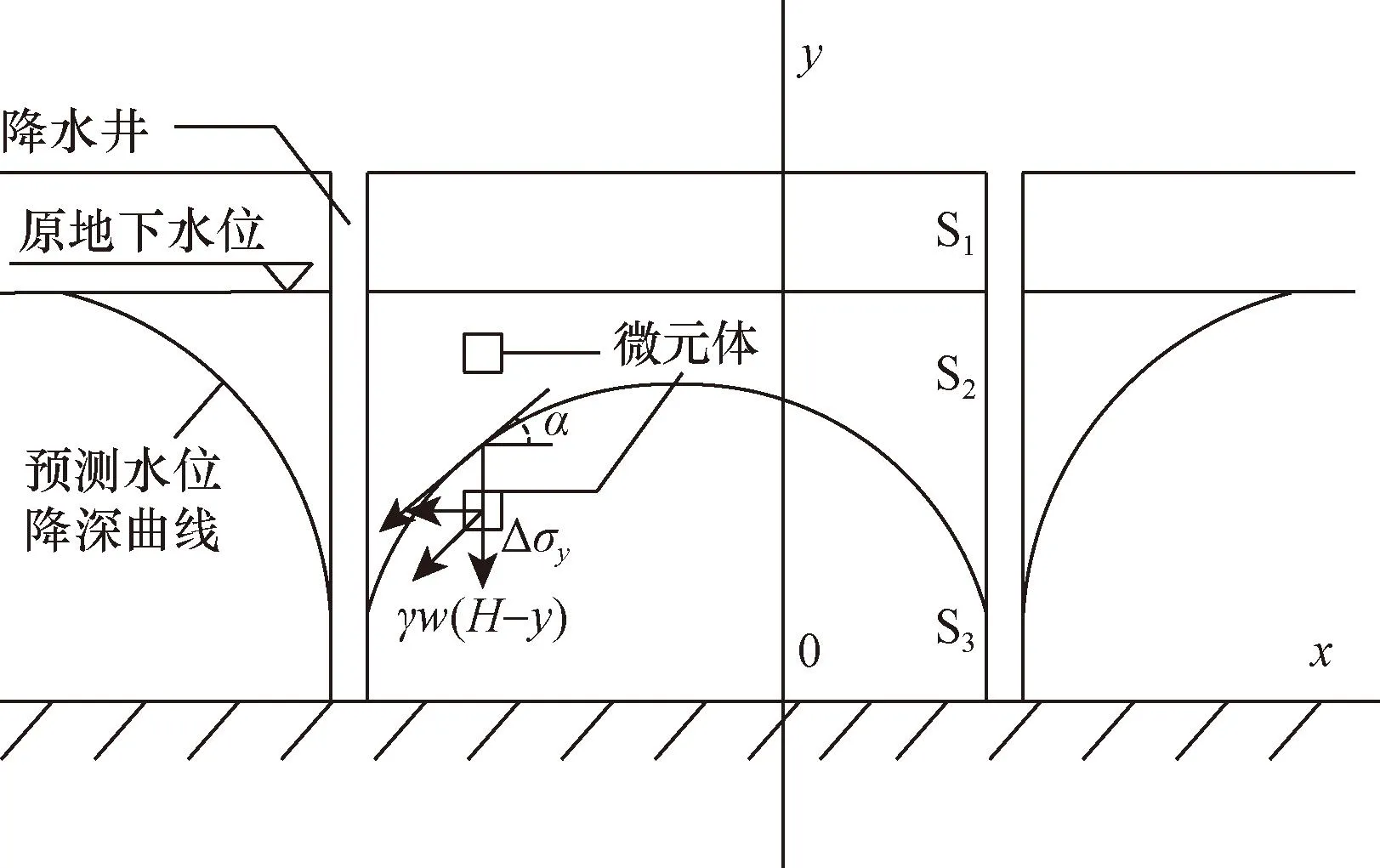
图3 降水后饱和区附加应力示意图Fig.3 Schematic diagram of additional stress in saturated area after precipitation wells

S2区可根据规范法计算附加应力和沉降值,即

Δσ′zi=γwzi

(6)

式中:Δσ′zi为疏干区S2内降水引起的地面下第i土层的平均附加有效应力,kPa;zi为第i层土中点至初始地下水位的垂直距离,m。

则疏干区S2的沉降值为

(7)

式中:s2为降水引起疏干区S2的沉降量,mm;Ψw为沉降计算经验系数,应根据地区工程经验取值,这里取1;Δhi为第i层土层厚度,m;Esi为第i层土的压缩模量, kPa。

如图4所示,S3区由于水力梯度作用下始终有渗流力作用,其渗流力方向这里取过计算点和最近降水井连线的垂直面内在该计算点处预测水位降深曲线切线方向,附加应力大小取值为渗流力的竖向分量。这里,使y沿着计算点和距离计算点最近的井方向求导,即y对x1求导,得计算点处渗流力方向。

图4 群井降水后最大渗流力方向示意图Fig.4 Schematic diagram of maximum seepage force direction of group wells after precipitation after precipitation wells

设距离计算点最近的井轴距离该计算点水平距离为x0,降水后水位值为y,则计算点处有

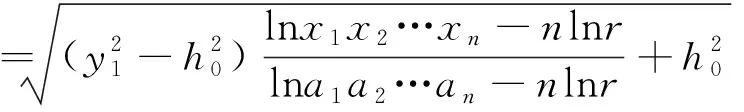
(8)

(9)

式中:α为最大渗流力方向与水平方向夹角。

考虑渗流力的竖向附加应力为

Δσy=γw(H-y)sinα

(10)

式(10)中:Δσy为计算点处竖向附加应力, kPa;H为潜水层厚度, m。

则饱和区S3的沉降值为

(11)

式(11)中:i∈(0,n],n为饱和区中土层数量。

综上,计算点处产生的土体总沉降s为

s=s1+s2+s3

(12)

2 工程实例

2.1 工程概况

北海魏桥翻车机房基坑项目工程位于滨州市,基坑为异形基坑,大体呈凹字形,东西长约130 m,南北长约50 m。拟建项目西侧为滨州北铁路线,铁路在基坑项目施工时未完成施工且仍在建设。拟建项目基础边线距离铁路线最近距离约为32 m。

为方便基坑开挖及基础施工,在基坑开挖前,先对基坑待开挖区域进行预降水处理。开挖前将水位降至待开挖面之下1 m处。为了保证基坑西侧铁路周边的安全,沿着铁路设置7 个监测断面对铁路沉降进行监测。铁路采用改良土对地基进行换填处理,为使土层参数更贴合于拟建项目场地《岩土工程勘察报告》中土层参数,排除改良土对降水沉降计算的影响,这里选取监测断面里铁路路基底部附近的DL监测点进行统计,铁路路基底部附近部分监测点及位置见图5。

2.2 水文条件及工程地质条件

根据拟建项目场地《岩土工程勘察报告》,该场区范围位于华北地台济阳拗陷区,地表被第四纪河流冲积及海陆交互相沉积物所覆盖,以黏性土、粉土、粉细砂为主,局部分布有软土地层。地貌特征表现为河流冲积平原,且微地貌发育。该场区地貌单元属于第四纪黄河三角洲冲积平原。根据野外钻探、静探揭露及室内土工试验结果,其土层物理力学指标如表1所示。

图5 基坑平面位置及铁路监测点布置图Fig.5 Plane position of foundation pit and layout of railway monitoring points

表1 场地土层物理力学性质指标Table 1 Physical and mechanical properties index of site soil layer

该场地地下水类型属于第四季潜水,铁路西侧有潮河河流,水的补给条件较好。2019年7月18日测得该场地地下水稳定水位埋深为0.3～0.7 m。地下水位随季节的变化而变化其年地下水位变化幅度为0.5～2.0 m,近3～5 年最高地下水位标高为2.5 m,历年地下水位标高为3 m。

2.3 基坑预降水方案

拟建项目开挖前进行预降水处理,以便基坑开挖干作业,在基坑待开挖区周围设置降水井。降水井井管采用无砂混凝土滤水管,过滤器半径200 mm,反滤层采用粗砾砂且不均匀系数小于2,采取设置滤网等措施保证从井中抽出的水不含泥土或砂。

预降水降至待开挖面以下后,基坑进行开挖、放坡等其他工序。考虑到尽可能减少对西侧铁路影响,并结合工程实例要求,降水井布置位置图见图6。

2.4 基坑周边铁路沉降监测结果

由于拟建场地的土层土质较为疏松,基坑开挖前预降水导致周围土体发生固结沉降是不可忽视的。如图7所示,在本项目中基坑开挖前预降水阶段,约第13天左右,地表沉降值基本稳定,降水对铁路影响最大的监测点是DL-4,其最大沉降值为9.2 mm。取降水井排布的几何中心为降水中心,各监测点沉降值大体上与距降水中心的距离呈反比。

如图7所示,预降水阶段可分为快速沉降阶段(第1～11天)、沉降减缓阶段(第11～13天)和沉降稳定阶段(第13～15天)。降水产生的降落漏斗主要在快速沉降阶段形成,因此该阶段发生的固结沉降速度快,沉降量大。在沉降减缓阶段,降水引起降落漏斗已基本形成,降落漏斗范围内土的重力排水已基本完成,土的固结压缩速度开始减缓。在沉降稳定阶段,土的固结压缩基本完成,土体固结压缩速度进一步减慢。

图7 铁路监测点时间-沉降实测曲线图Fig.7 Railway monitoring point time-settlement measured curve

在沉降监测中,监测点DL-5与上述各监测点沉降值大体上与距降水中心的距离呈反比的结论相悖,分析其原因为:铁路未完成施工,铁路坡脚处施工的车辆以及其他器具带来的地表荷载导致监测点附近土体被压实,监测点处相对周围土体略微隆起,使监测沉降数值变小。

3 数值模拟

3.1 模型建立

群井用井单元进行模拟,井单元排布与工程实例相同,其排布见图6所示,井单元长度16.8 m。井单元与多个土层相交时,其周围土层通过的水流量符合饱和渗透率和井单元相交深度的函数,实际抽水量取决于周围土体渗透系数以及井单元参数设置。设定井单元最大抽水流量为200 m3/d,井内最低水位设置为井底标高。计算模式采用流固耦合,可以较好地模拟土体变形和孔压随时间变化。计算时间为15 d,与实例工况相同。

对于基坑西侧铁路因前期有铁路路基对地表的压缩固结作用,模型用表面荷载模拟铁路路基自重对地表沉降影响。在井单元抽水前,通过对表面荷载产生位移进行清零的方式,避免表面荷载影响井单元抽水引起的地表沉降。模型建模见图8。

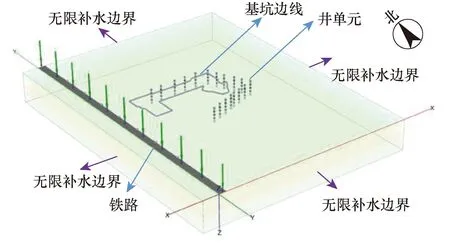
图8 基坑预降水有限元模型图Fig.8 Finite element model diagram of foundation pit pre-excavation dewatering

3.2 群井效应下井流量和孔压数值分析

将井单元按照如图6所示进行编号,统计各井单元在计算步结束时的抽水量大小,如图9所示。井单元的实际抽水量与土层渗透系数、井深、降水井排布方式等相关因素有关,在群井效应的影响下,井1和井18因位于群井最外侧,受到其他井的影响最小,其补给条件优于其他井,井周围土体提供井流量最大,井流量分别为166.1 m3/d和128.2 m3/d。其余井受周围井影响较大,井流量在41.8～79.9 m3/d。

图10和图11为过图6中1-1剖面的降水前后孔隙水压力云图,孔隙水压为0的位置代表地下水位。如图10所示,原地下水位是水平的,土层中水在井单元作用下逐渐疏干,原地下水位逐渐下降,计算步结束时形成群井作用下的降落漏斗。模型建模考虑群井效应,井单元相互之间存在关系,任意井单元的补水边界受其周围井单元影响,原地下水位经过抽水后形成的降落漏斗不再是单井降落漏斗曲线[18],而是受群井共同作用下的曲线,如图11所示。在井单元疏干作用下,越靠近井单元疏干效果越明显,疏干区越大,同时抽水作用形成的水力梯度也越大。

图9 预降水井流量柱状图Fig.9 Bar chart of pre-excavation dewatering well flow

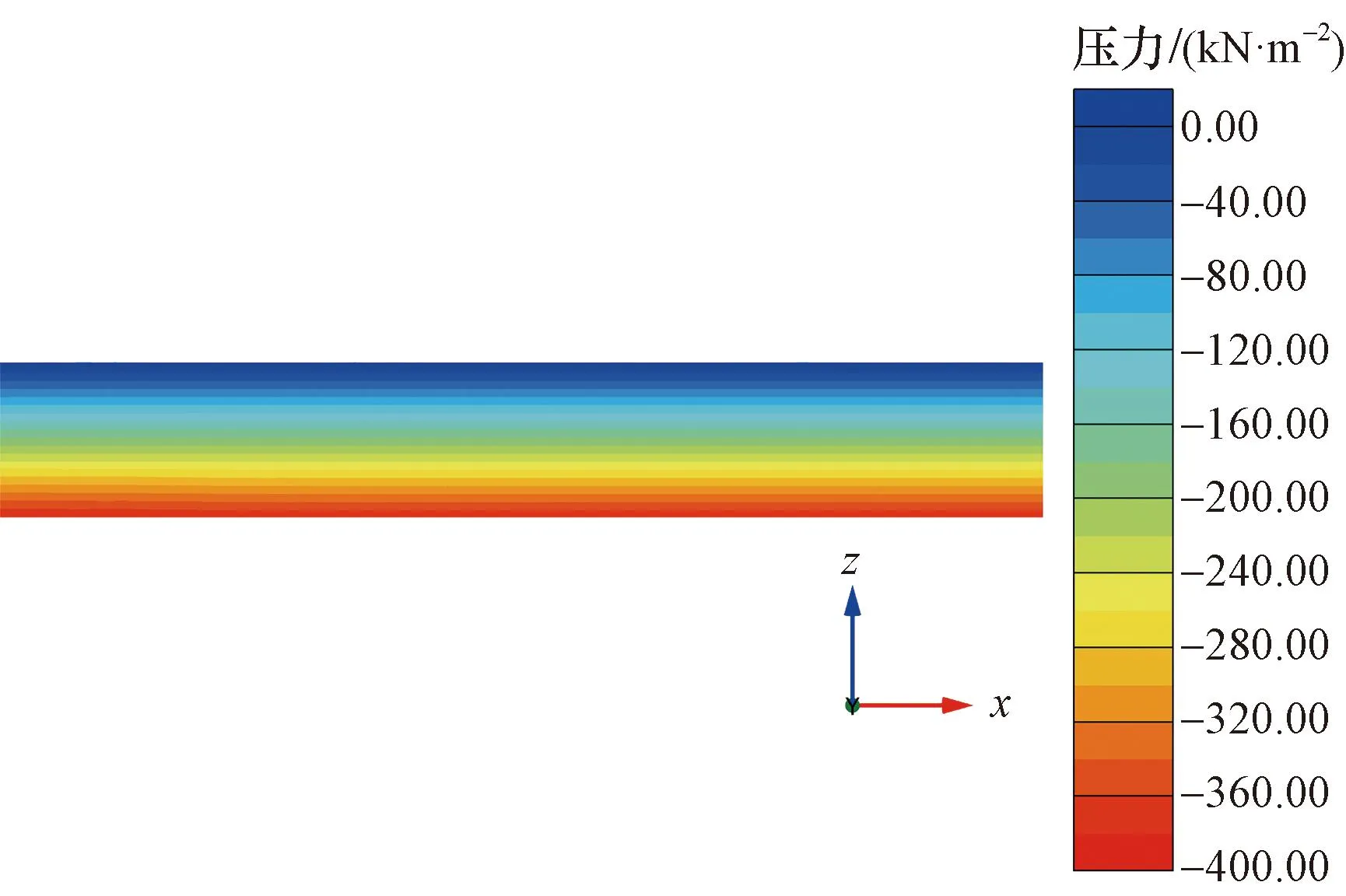
图10 预降水前孔隙水压力云图Fig.10 Cloud map of pore water pressure before pre-excavation dewatering

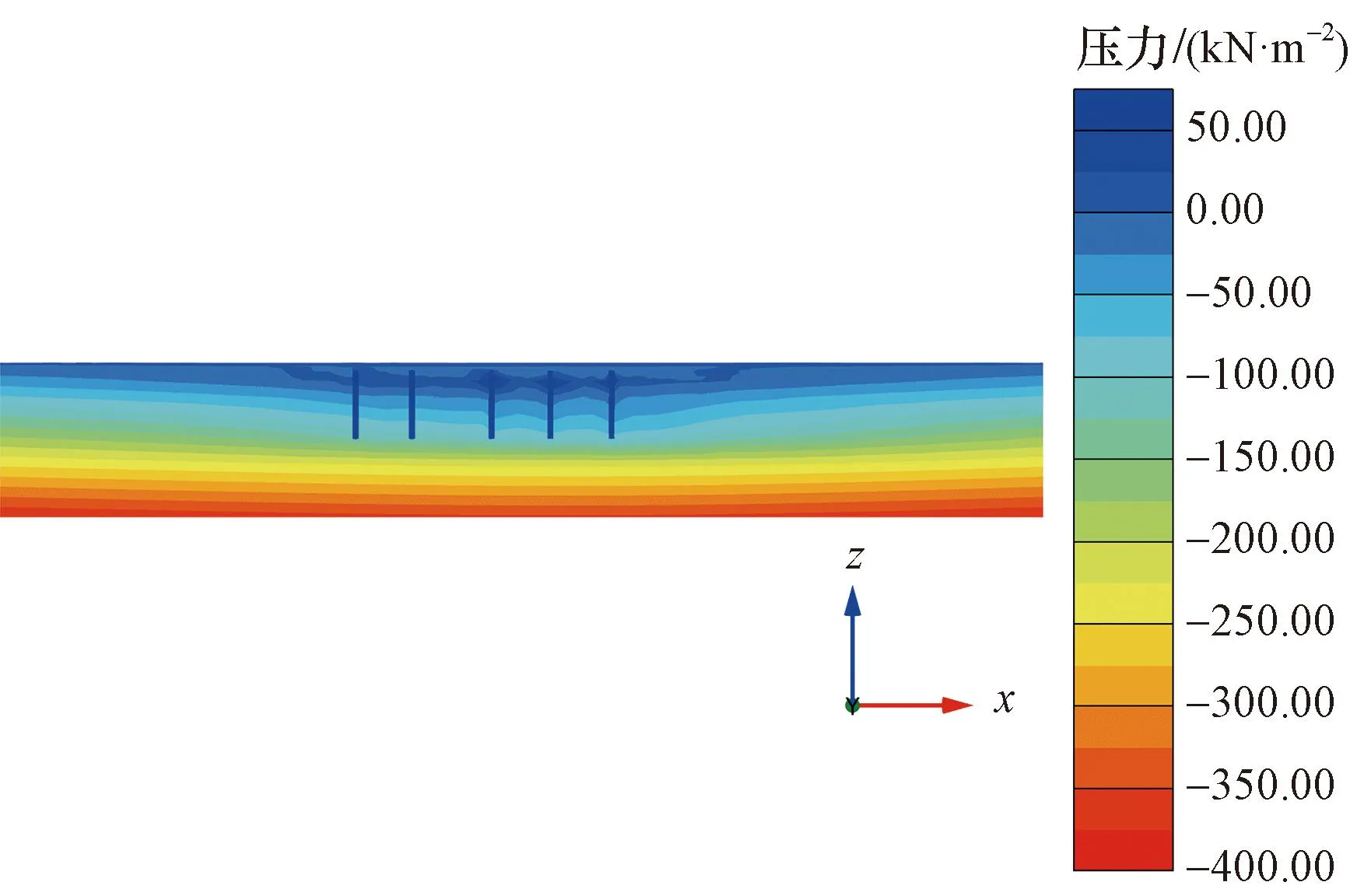
图11 预降水后孔隙水压力云图Fig.11 Cloud map of pore water pressure after pre-excavation dewatering

3.3 预降水后沉降量

模型主要研究降水对地表沉降影响,用时间来控制水位的降深和降水固结速度,模拟降水时间与工程实例降水时间相同。图12为土体在井单元抽水作用下的竖向位移云图。在抽水后,地表发生沉降,在降水中心附近发生最大沉降,距降水中心的距离越大其沉降值越小,西侧铁路在沉降影响范围内。边界附近沉降数值约为0,表明了模型所取边界大小的合理性。

西侧铁路监测点沉降量随时间变化曲线见图13。在降水过程中,沉降值随时间的延长逐渐增大,最终趋于稳定,沉降值与时间的关系呈现明显的非线性关系,与图7的实测数据相比,有大致相同的沉降趋势。数值模拟结果表明:DL-3、DL-4和DL-5经预降水后的沉降值最大,其距离降水中心距离最近,井单元的疏干作用最显著,故受降水影响最大;DL-2和DL-6监测点位置不同,但是其沉降数值大体相同,表明预降水引起沉降是多井互相作用的结果,在不同地理位置可能会引起相似的疏干效果,产生基本一致的沉降;根据监测点沉降数据与其位置关系可以得出降水引起的沉降值大体与距降水中心的距离呈反比的结论。

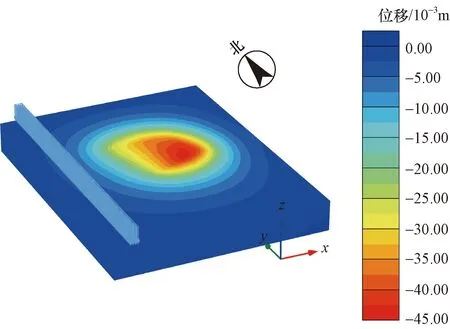
图12 预降水后竖向位移云图Fig.12 Vertical displacement cloud image after pre-excavation dewatering

数值模拟预降水阶段与工程实例相似,同样可分为快速沉降阶段(第1～2天)、沉降减缓阶段(第3～6天)和沉降稳定阶段(第7～15天),其与工程实例预降水阶段对比如图14所示。数值模拟快速沉降阶段相对工程实例时间短,沉降减缓阶段相对更长,其原因是:模拟的土层渗透系数水平向各向同性,井单元抽水时形成的降落漏斗速度更快,固结压缩沉降速度也更快,也就更先进入沉降减缓阶段。而在工程实例中,土体受自重等影响,水平向渗透系数一般大于竖向渗透系数,土体渗透系数各向异性,降水井疏干效果受水平和竖向渗透系数共同决定,所形成的降落漏斗的速度受较小的竖向渗透系数的限制,会更加缓慢,其快速沉降阶段占比也就更大;数值模拟的最大井单元抽水量是井1的166.1 m3/d,未达到所设计的最大抽水量200 m3/d,井单元的抽水能力始终大于周围土体的供水能力,在井单元周围形成较大的水力梯度,降落漏斗的形成速度更快。在工程实例中,地下水位较高,降水井周围土体供水量大,降水井容易出现抽水量不及周围土体补水量的情况,此时水力梯度相对数值模拟更小。在这种水力梯度差异的情况下,数值模拟降落漏斗的形成速度比工程实例快,土体固结压缩更快,快速沉降阶段持续时间短且先进入沉降减缓阶段;数值模拟的井单元始终在工作,工程实例降水井存在井堵塞、污染的问题,需要对问题井进行清洗,清洗时停止抽水。所以,数值模拟井单元整体上工作时长相对工程实例更长,土体固结速度更快,快速沉降阶段更快结束,先一步进入沉降减缓阶段。

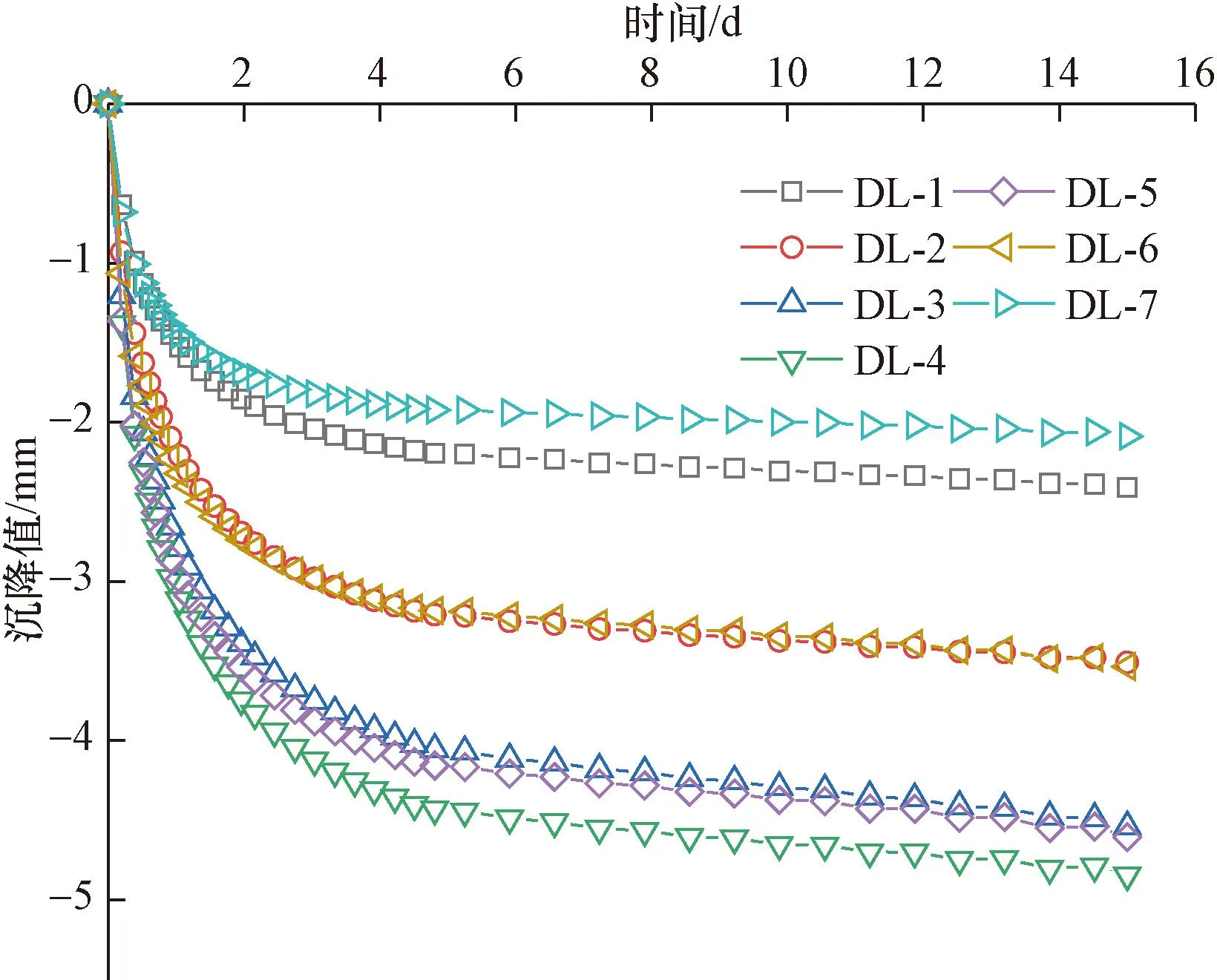
图13 铁路监测点时间-沉降值模拟曲线图Fig.13 Time-settlement simulation curve of railway monitoring point

图14 预降水沉降阶段分析图Fig.14 Analysis diagram of pre-excavation dewatering settlement stage

4 分析对比

选用所提出理论计算方法和数值模拟进行预降水引起地表沉降值求解,用规范法和工程实测进行对比并验证分析所用方法的合理性,进一步揭示沉降数值与距降水中心距离的关系,不同计算方法距离-沉降对比曲线图如图15所示。对比结果具有以下几条特点。

(1)整体上,规范法计算沉降值最大,其计算值较为保守,数值模拟值与理论计算方法值更加接近于实测值,表明理论计算和数值模拟方法更贴近于实际工程。所用理论计算和数值模拟方法值与实测沉降值有相似的沉降规律,即大体呈现沉降值与距降水中心的距离呈反比,说明所用方法能够相对准确地反映预降水引起地表沉降变化趋势。

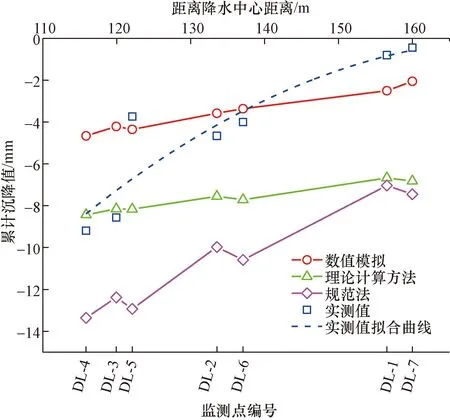
图15 不同计算方法距离-沉降对比曲线图Fig.15 Distance-settlement contrast curve of different calculation methods

(2)理论计算方法值在与距降水中心的距离较近时更为接近实测值,距离较远时大于实测值,其原因是:理论计算方法的计算点距降水中心的距离较近时,有较大的水力梯,考虑渗流力作为附加应力符合疏干土体受力状态,计算沉降值更接近实测值;计算点与距降水中心的距离较远时,基于裘布衣假设的理论计算方法的潜水层是水平的,忽略了河流补给的影响,而工程实例中受西侧河流补给的影响,降水井疏干效果减弱,理论计算值也就比实测值更大。

(3)计算点距降水中心的距离较远时,数值模拟值与实测值更为接近,距离较近时小于实测值,其原因是:数值模拟的四周边界条件是无限补水边界,工程实例基坑西侧河流补给边界可近似看作无限补给边界。数值模拟求解中,计算点距降水中心距离较远时,模型南北两侧无限补水边界会限制井单元疏干作用,使得求解沉降数值比实测值偏小;计算点距降水中心距离较近时,模型西侧无限补水边界起补水的主导作用,更加接近西侧有河流补给的工程实例,求解的沉降值更接近实测值。

5 结论

通过考虑群井效应的理论计算和数值模拟两种方法,对预降水引发地表沉降求解,并揭示群井效应下抽水流量规律,展示预降水孔压变化过程,得到以下结论。

(1)在考虑群井效应前提下,提出预测水位降深曲线,用该曲线和原地下水位进行分区,疏干区采用规范法计算附加应力,饱和区考虑群井效应下渗流力为附加应力,最后用分层总和法分别计算各区沉降量,叠加后得最终沉降量。该求解沉降量的方法与规范法相比有更高的精确度,在计算点与距降水中心的距离较近时与实测值吻合较好。

(2)基于PLAXIS 3D,用井单元模拟降水井,流固耦合对预降水期间周围地表沉降求解,展示了预降水前后孔压变化,揭示了群井效应下群井抽水流量规律:土层参数相同,井单元设置相同情况下,补给条件越好,抽水量越大。

(3)PLAXIS 3D模拟沉降结果受无限补水边界的影响,在计算与距降水中心的距离较远的监测点时与实测值吻合较好,其计算结果与实测数据有相似的沉降规律,均分为快速沉降阶段、沉降减缓阶段和沉降稳定阶段,但各阶段在总阶段占比不同。

(4)结合工程实例项目监测数据和规范法验证理论计算方法和数值模拟的合理性。理论计算、数值模拟方法值和实测沉降值都有沉降值大体与距降水中心的距离呈反比的沉降规律,能够相对准确地反映预降水引起地表沉降变化趋势,相比规范法有更高的精度,可以较为有效地为相似潜水层基坑预降水工程提供借鉴。