改性1-3型压电复合材料理论模型与仿真

王嘉程,张金英,仲 超,秦 雷

(1.北京理工大学 精密光电测试仪器及技术北京市重点实验室, 北京100081; 2. 北京理工大学 长三角研究院, 浙江 嘉兴314001; 3.北京信息科技大学 传感器北京市重点实验室, 北京100101)

0 引言

超声换能器是实现电声信号相互转化的一类电子器件,目前广泛应用于海洋探测、医学成像、水声定位等技术领域[1-2]。1-3型压电复合材料作为换能器常用的敏感材料,因其具备良好的机电特性和简易的制备工艺而备受研究者青睐。

1-3型压电复合材料是由一维线性排列压电小柱和三维连通聚合物构成的两相复合材料,聚合物可有效地将压电小柱进行分离,且能抑制纯陶瓷材料的平面耦合[3]。近年来,相关研究者对1-3型结构进行了优化,制成了系列1-3衍生型结构,以提升材料的机电耦合系数、声学匹配能力、力学稳定性等性能。Li等[4]在保留1-3型压电材料连通方式的基础上,加入陶瓷基底作为复合支撑,制成具有高稳定性和高机电耦合系数的1-3-2型压电复合材料。Qin等[5]采用环氧树脂与硅橡胶的两相包裹结构作为聚合物相,制备出1-1-3型压电复合材料,使材料的机电转换能力和声学匹配能力均得到有效提升。He等[6]采用3D打印技术制备了陶瓷占比40%的空气基1-3型压电复合材料,并通过实验验证了用该材料制备出的空气耦合换能器具备较低的信噪比。Rouffaud等[7]改变了压电相的空间排布,制成超晶胞型1-3型压电复合材料,不但减少了传统切割-灌注法制备时出现的杂散现象,而且在机电性能方面有显著提高。由此可见,填充聚合物可有效改善材料的厚度振动模,此方式不仅提升了压电陶瓷原有的压电常数与机械振动等物理性能,同时有效地降低了材料的特性阻抗,这使其在振动过程中可同时实现高机电转换效率和良好的声学匹配能力。

目前1-3型压电复合材料及其衍生类设计[5]多以压电陶瓷和刚性环氧树脂两种材料制备而成,制成的压电振子刚性较强且不易弯曲,故对水下无人航行器和高频声呐等曲面壳体设备的共形仍具有较大的局限性;另一方面,环氧树脂可让复合材料中的压电小柱有效分离,同时还可降低材料自身的特性阻抗,但是环氧树脂自身的刚性限制了机电耦合系数的进一步提高(约为0.6[3])。

本文提出一种基于压电陶瓷、环氧树脂和硅橡胶三相复合的改性1-3型压电复合材料。第三相柔性橡胶的引入不仅实现了传统1-3型压电复合材料的单向弯曲能力,而且橡胶的柔性可促进压电小柱的机械振动,使材料的厚度机电耦合系数得到进一步加强。本文利用本构关系对改性1-3型压电复合材料的理论模型进行了推导,分析了陶瓷相体积分数对材料参数的影响;利用ANSYS有限元分析软件对不同结构参数的复合材料1/4单元进行了仿真,并对理论推导进行了验证与评估,为后续压电振子的制备提供了较好的理论基础。

1 改性1-3型压电复合材料结构

改性1-3型压电复合材料结构如图1所示。 由图可看出,本文提出的改性结构与传统结构在连通结构上同属于1-3型,故属于1-3型衍生类压电复合材料。环氧树脂和硅橡胶在z方向上呈并联结构,二者共同包裹于压电陶瓷柱的四周,对复合材料整体的振动起不同作用。环氧树脂作为刚性聚合物相,其杨氏模量较高,可对复合材料起支撑作用,提高复合材料力学稳定性。硅橡胶为柔性聚合物相,其自身的柔性较强,能使压电陶瓷柱的振动抑制达到最小,进而提升材料的厚度振动。此外,硅橡胶可加强复合材料单方向(y方向)的柔性,使复合材料满足一维弯曲特点,实现了1-3型压电复合材料共型弯曲,在未来研制弧面换能器及其基阵方面具有较大的应用前景。

图1 改性1-3型压电复合材料三维结构图

2 改性1-3型压电复合材料的理论分析

2.1 改性1-3型压电复合材料理论模型的推导

本文研究的改性结构采用1-3连通型,可利用Newnhams的串并联分析[8]对改性1-3型压电复合材料的理论模型进行推导。由于压电陶瓷相和环氧树脂相在y方向呈2-2型,陶瓷-环氧复合相与硅橡胶相在x方向呈2-2型,因此,改性1-3型压电复合材料的理论模型可拆分成陶瓷-环氧复合相、陶瓷-环氧复合材料相与硅橡胶相2-2复合两部分考虑,拆分结构如图2所示。

图2 改性1-3型压电复合材料的等效拆分结构

首先推导陶瓷-环氧2-2型复合相模型。假定复合材料内部为均匀介质,不考虑材料振动时的非线性影响,沿厚度方向极化的压电陶瓷可按e型压电方程[8]展开:

(1)

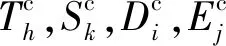
环氧树脂作为各向同性体,其对应的压电方程可按下式展开:

(2)

根据改性1-3型结构的特殊性可提出5项理论假设:

1) 由于电极被覆于复合材料上下端面,电场方向与z轴平行,横向电场为0,即:

(3)

2) 复合材料整体沿厚度方向做伸缩振动,剪应变为0,即:

(4)

根据前两项假设,压电陶瓷相和环氧树脂相的压电方程可分别化简为

(5)

(6)

压电陶瓷相和环氧树脂相采用2-2连通形式复合,由混合场理论,理想状态下的复合材料,其内部各力学和电学分量可采用组成相与其体积分数加权的形式表示,由此可假设:

(7)

式中:上角标“ce”表示陶瓷-环氧复合相;vc为陶瓷-环氧复合相中压电陶瓷相的体积分数;ve为环氧树脂相的体积分数。

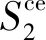
(8)

(9)

由第3)-5)假设可知,S1、T2、S3和E3可作为自变量来表示T1、S2、T3和D3因变量,于是式(5)、(6)可分别化为

(10)

(11)

根据第3)-5)项假设关系,将式(10)、(11)按压电陶瓷相和环氧树脂相的体积分数进行整合,则有:

(12)

其中:

vcMc+veMe=

(13)

(14)

结合式(12)-(14),将矩阵转换为e型压电方程的矩阵形式,则有:

(15)

由矩阵的特殊性得到对应陶瓷-环氧复合材料的电弹系数:

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

将陶瓷-环氧复合相视为整体,由图2可知,该复合相与硅橡胶相按2-2再次连通,最后形成改性1-3型结构,且复合相与硅橡胶相沿x方向串联,y方向并联,类比上述推导过程,可得到本构关系:

(26)

式(26)为改性1-3型压电复合材料的压电方程,其中:

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

式中:上角标“s”表示硅橡胶相;“ces”表示改性1-3型压电复合材料;v1为陶瓷-环氧复合相体积分数;vs为硅橡胶体积分数。

根据IEEE标准[9],压电复合材料的厚度机电耦合系数kt、厚度频率常数Nt及等效密度ρt分别为

(37)

ρt=v1(vcρc+veρe)+vsρs

(38)

(39)

式中:ρt为复合材料等效密度;ρc,ρe,ρs分别为压电陶瓷、环氧树脂和硅橡胶的等效密度。

将式(26)对应参数代入式(37)-(39)即求得kt、Nt、ρt。

2.2 改性1-3型压电复合材料的性能参数计算

为分析和评估复合材料性能,本文选取PZT-5A压电陶瓷、618环氧树脂和704硅橡胶作为改性1-3型压电复合材料的3个具体组成相进行分析。其中传统1-3型压电复合材料作为对照,选取PZT-5A和618环氧树脂作为其组成相,利用Matlab 2019软件对第2.1节推导的性能参数进行数值计算,组成相的材料参数如表1所示。

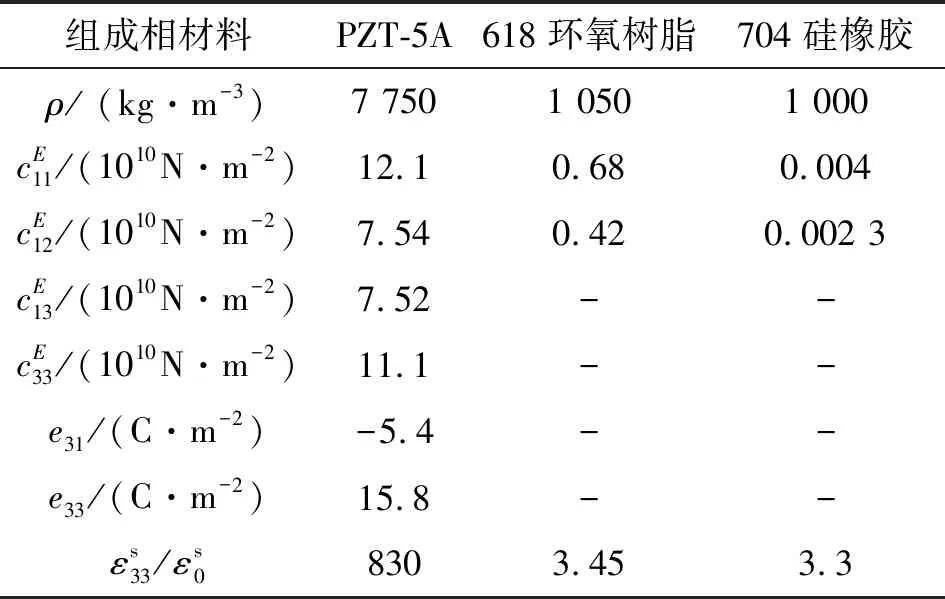
表1 组成相的材料参数

将表1中参数代入相关的性能参数计算式,可得到在不同陶瓷-环氧复合相体积分数(选取0.1、0.2、0.3、0.5和0.9)条件下,性能参数随陶瓷-环氧复合相中压电陶瓷相体积分数变化的关系曲线。

图3为不同陶瓷-环氧复合相v1条件下,kt与压电陶瓷相vc的关系曲线。kt用于表征压电体能量转换强度的重要参数,kt值越高,说明复合材料机电转换能力越强,对应超声换能器的灵敏度越高。由图3可知,随着v1逐渐升高,复合材料的kt值先迅速增加,后稳定在0.68左右,说明硅橡胶材料的引入会促进复合材料的机电转换能力,但引入量过高会对厚度能量的转换产生一定影响。当vc<0.2时,复合材料中压电陶瓷的含量较少,kt值提升速度较显著;当0.2≤vc≤0.6时,复合材料kt值的提升速度变缓直至增加到最大值。当vc≥0.8时,压电陶瓷的含量逐渐达到饱和,复合材料的平面耦合更显著,这将影响复合材料整体的厚度振动能量,kt值下降;当压电陶瓷的体积分数较高时,不同v1条件改性复合材料的kt值相比传统1-3型下降效果均不明显,这是由于当vc趋近于1.0时,改性1-3型将变为陶瓷-硅橡胶2-2型复合材料,亦可大幅减小厚度振动能量的损失。

图3 kt随压电陶瓷相体积分数vc的变化关系

根据图3,传统1-3型的kt最大值趋于0.65,而改性1-3型压电复合材料的kt值高于传统1-3型的kt值,其最大kt值趋于0.68,提升了4.6%,说明硅橡胶的柔性对陶瓷柱的振动起到激励效果,进一步促进了复合材料的机电转换能力,而组成相结构的改进也有效地解决了刚性环氧树脂对kt值的限制问题。因此,对于研制高kt值压电复合材料,压电陶瓷相体积分数vc的优选范围应满足0.6≤vc≤0.7,陶瓷-环氧复合材料体积分数v1的优选范围应满足v1≥0.2。

图4为不同v1下,ρt与压电陶瓷相vc的关系曲线。当vc逐渐增加时,ρt呈现线性递增变化,且陶瓷-环氧复合材料v1越高,ρt的变化越显著,这是由于压电陶瓷密度是聚合物密度的7倍,压电陶瓷体积分数越高,复合材料整体的密度越高,密度变化率也越快。此外,由于硅橡胶相的缘故,几种不同v1条件改性1-3型压电复合材料密度均低于传统1-3型,而密度参数会影响换能器在水中的声学匹配能力,在同等纵向声速前提下,复合材料的密度越小,换能器与水介质的声学匹配性越好,因此,v1选取含量应尽可能低。

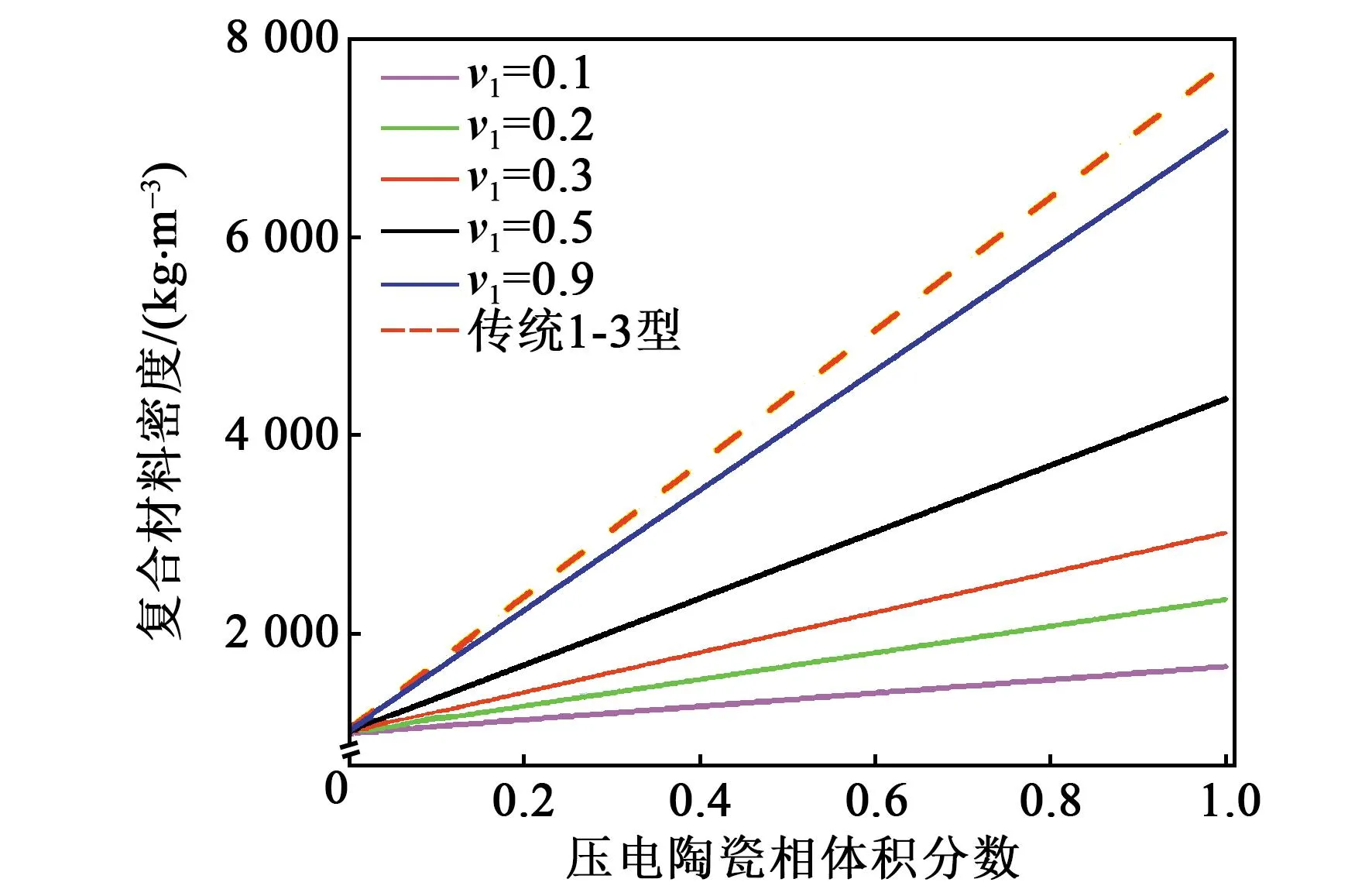
图4 ρt随压电陶瓷相体积分数vc的变化关系

图5为不同v1下,Nt与压电陶瓷相体积分数vc的关系曲线。Nt常用于评估压电材料的共振频率。对于1-3连通型的复合材料,这里电场与振动方向平行,故Nt值为反谐振频率与厚度的乘积。由图5可知,复合材料中v1的越大,其Nt值越大,这与压电陶瓷自身Nt值较高的因素有关。随着vc逐渐升高,陶瓷-环氧复合相中的压电陶瓷逐渐达至饱和,Nt值的上升逐渐趋于平缓。改性1-3型的Nt值在不同复合相v1条件下均低于传统1-3型,这说明硅橡胶的加入对降低复合材料工作频率具有显著效果,在相同厚度与外形尺寸条件下,硅橡胶加入量越大,复合材料的低频效果更显著,在研制轻质量且满足共型特点的超声换能器方面具有很大优势。

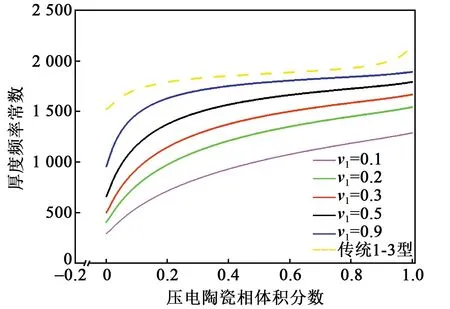
图5 Nt随压电陶瓷相体积分数vc的变化关系

综上所述,组成相的改进对1-3型压电复合材料的提升具有重要的指导意义,不但解决了刚性聚合物对机电能量转换的限制问题,促进了机电耦合系数的提高,而且有望拓宽1-3型压电复合材料的应用领域。对于满足上述高性能超声换能器需求,改性1-3型压电复合材料中陶瓷-环氧复合相体积分数v1=0.2～0.5,而陶瓷-环氧复合相中压电陶瓷体积分数vc=0.6～0.7。

3 改性1-3型压电复合材料的有限元仿真

有限元分析是一种以变分原理和剖分插值为理论基础的数学逼近方法,常用于解决力、电、声、光等多元物理场的工程问题。本文利用ANSYS 15.0软件对改性1-3型压电复合材料进行有限元仿真,并将仿真结果与理论计算进行对比验证。为便于计算,本文选取复合材料的1/4周期单元进行仿真,根据第2节得出的优选范围,本文拟选取v1=0.5的复合材料模型进行理论验证。

改性1-3型压电复合材料的单元结构如图6所示。设复合材料的厚度h=2.5 mm,压电陶瓷柱宽a=1 mm,环氧树脂宽度为b,硅橡胶宽度为c。由已知v1=0.5可得硅橡胶体积分数vs=c/(a+c)=0.5,则c=1 mm,b可根据压电陶瓷相所占陶瓷-环氧复合相的体积分数vc进行设定,如表2所示。

表2 环氧树脂宽度b与陶瓷体积分数vc对应关系

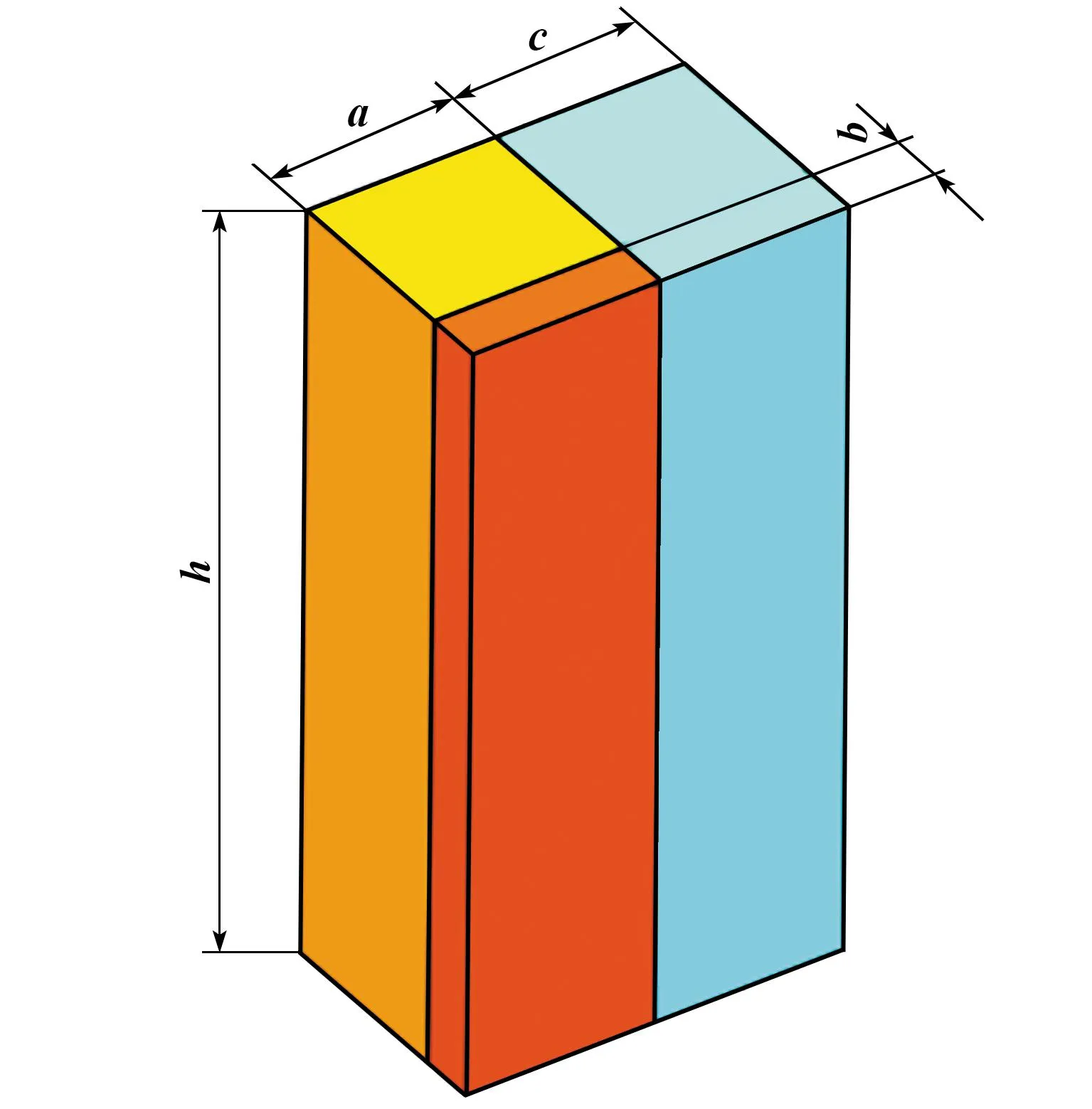
图6 改性1-3型压电复合材料的周期单元

根据表2中尺寸参数,在ANSYS前处理模块中对1/4周期单元进行建模、材料赋值与网格划分,其中压电陶瓷、环氧树脂和硅橡胶的材料参数与表1相同。网格采用正六面体结构进行划分,为保证计算精度和节约时间成本,这里设网格尺寸为0.1 mm,并采用自动扫掠功能进行有限元分割。网格分割完后,对材料的侧壁施加对称边界,并在上下端面施加幅值为1 V的简谐交流电压后求解计算。

在后处理模块中,对不同vc条件下复合材料导纳Y值进行提取,得到仿真曲线如图7所示。

图7 不同vc条件下改性1-3型压电复合材料的导纳结果

压电材料的性能参数可通过阻抗或导纳曲线获取。由图7可知,v1=0.5时,不同陶瓷相体积分数vc的改性1-3型压电复合材料的导纳信息。谐振频率fs是压电材料因外届激励而产生最大响应时的频率。反谐振频率fp为最小响应时的频率,则压电材料的kt和Nt分别[10]为

(40)

Nt=fph

(41)

由于仿真和理论采用同一密度公式,故本节只进行kt和Nt的理论验证。读取图7中各单元的谐振频率和反谐振频率,将其代入式(40)、(41)中计算求解,然后将计算结果与理论进行对比,如图8所示。

图8 理论计算-仿真结果对比曲线

由图8(a)可看出,仿真结果与理论计算的趋势基本保持一致,验证了理论模型的有效性。当vc=0.2时,复合材料的kt值高达0.70,相比于一般传统1-3型压电复合材料(约为0.6)最大可提升14.2%。该结果肯定了硅橡胶相的优势,不仅促进了复合材料的厚度振动,同时也可让复合材料的厚度模能量高度集中。从仿真数据看,陶瓷相体积分数vc变化过程中,kt值波动较小,且基本稳定(0.68～0.69),说明改性1-3型具备比传统1-3型更优异且稳定的机电转换能力。

由图8(b)可看出,整体上仿真结果与理论计算具有较好的一致性。当vc≤0.4时,仿真结果与理论计算出现一定的偏差,其中仿真结果使复合材料的Nt趋近于常值,其原因可能与硅橡胶产生的非线性变化有关。本文借助Newnhams推导的理论模型近似认为复合材料内部为均匀的线性变化,忽略了高弹性聚合物的非线性因素,这也是Nt的理论计算与仿真结果产生偏离的主要因素。

综上所述,经组成相改进后的1-3型压电复合材料具有比传统1-3型更显著的性能优势,硅橡胶相的填充不仅促进了复合材料的机电转换能力,同时降低了其自身密度和频率常数,使传统1-3型压电复合材料的应用空间得到有效拓展。本文推导的理论模型与有限元仿真结果均表征了改性1-3型压电复合材料优异的性能,结合尺寸优选范围可为后续样品的制备提供较好的理论基础。

4 结束语

本文提出了一种基于压电陶瓷、环氧树脂和硅橡胶三相复合的改性1-3型压电复合材料。根据Newnhams串并联分析,建立了该复合材料的理论模型并利用Matlab软件进行了数值计算,结合计算结果分析了材料的性能优势,给出了尺寸参数的优选范围。通过ANSYS软件对改性1-3型压电复合材料进行了有限元仿真,并将仿真值与理论结果进行了对比。结果表明,本文推导的理论模型与有限元仿真结果均表征了改性1-3型压电复合材料优异的性能,而且理论计算和仿真结果具有较好的一致性,证明了理论模型评估材料性能的准确性,结合优选范围可为后续样品的实验与生产提供理论指导。