双波段大孔径角声光可调滤光器

张泽红,王智林,何晓亮,刘 玲

(中国电子科技集团公司 第二十六研究所,重庆 400060)

0 引言

与传统的分光元件相比,非共线声光可调滤光器(简称“滤光器”)具有孔径角大,集光能力强,稳定性强,调谐灵活快速,信号接收和处理方便等优点,在光谱成像领域具有很高的应用价值[1]。

常用滤光器均针对单个波段进行设计,把可见光与中波波段设计在同一滤光器上,为可见光光谱成像系统和中波光谱成像系统集成为一个系统创造了条件。它能同时对目标的可见光与中红外波段进行快速光谱成像,在充分挖掘生物细胞组织的可见光与中波红外光谱特征信息方面具有重要意义。

为了提高滤光器的集光能力,一般都采用“切面平行动量匹配条件”理论[2],把滤光器设计成大孔径角。在设计大孔径角滤光器时,对于同一入射极角θi(入射光与光轴的夹角),入射e光[3]所需最佳超声极角(超声波与光轴的夹角)为θe,入射o光[3]所需最佳超声极角为θo。θo和θe不同,其原因是晶体的o光和e光的折射率不同(o光和e光的折射率相同的晶体无法制作大孔径角滤光器)。

把入射e光设计成可见光波段,入射o光设计成中波波段,这时滤光器可同时兼顾可见光与中波波段的双波段大孔径角声光可调滤光器。

1 理论分析

1.1 基本原理

图1为双波段大孔径角声光可调滤光器基本原理,其特点是1个共同的入射极角θi、2个不同的超声极角θo和θe。共同的入射极角θi是指入射o 、e光采用相同的入射角进入声光晶体,即共用一个光路入射。超声极角θo(超声波Kao与光轴的夹角,也是通声面2法线与光轴的夹角)专门针对入射o光设计,能满足入射o 光(中波波段)的大孔径角要求;超声极角θe(超声波Kae与光轴的夹角,也是通声面1法线与光轴的夹角)专门针对入射e光设计,能满足入射e光(可见光波段)的大孔径角要求。这种双波段大孔径角声光可调滤光器声光介质的两个通声面(通声面1和通声面2)相差角度β=θo-θe。

图1 双波段大孔径角声光可调滤光器原理图

对于入射e光,滤出得到的衍射光为o光,其波矢量布局如图2所示。[001]轴为晶体光轴,o光的折射率曲面是半径为no的圆,e光的折射率曲面是以长短轴分别为ne、no的椭圆。入射光Ki与超声波Kae发生声光互作用,滤出衍射光Kde,衍射光与光轴的夹角为衍射光极角θde。根据非同向声光可调滤光器“切面平行动量匹配条件”理论,结合图2,入射e光获得大孔径角的条件:

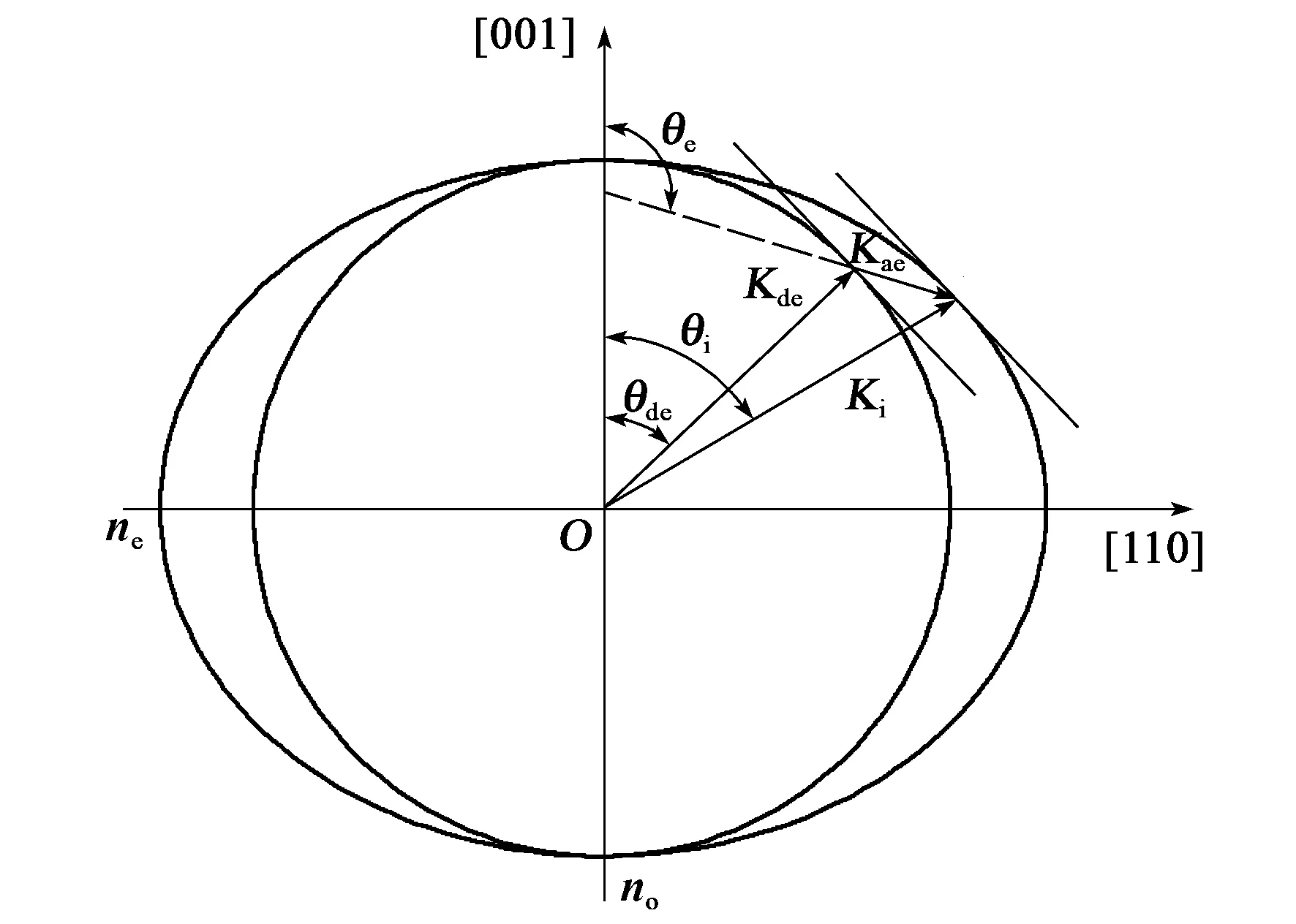
图2 入射光为e光时的波矢量布局

Kde=Ki-Kae

(1)

同理,对于入射o光,滤出得到的衍射光为e光,其波矢量布局如图3所示。入射光Ki与超声波Kao发生声光互作用滤出衍射光Kdo,衍射光与光轴的夹角为衍射光极角θdo。结合图3,入射o光获得大孔径角的条件:

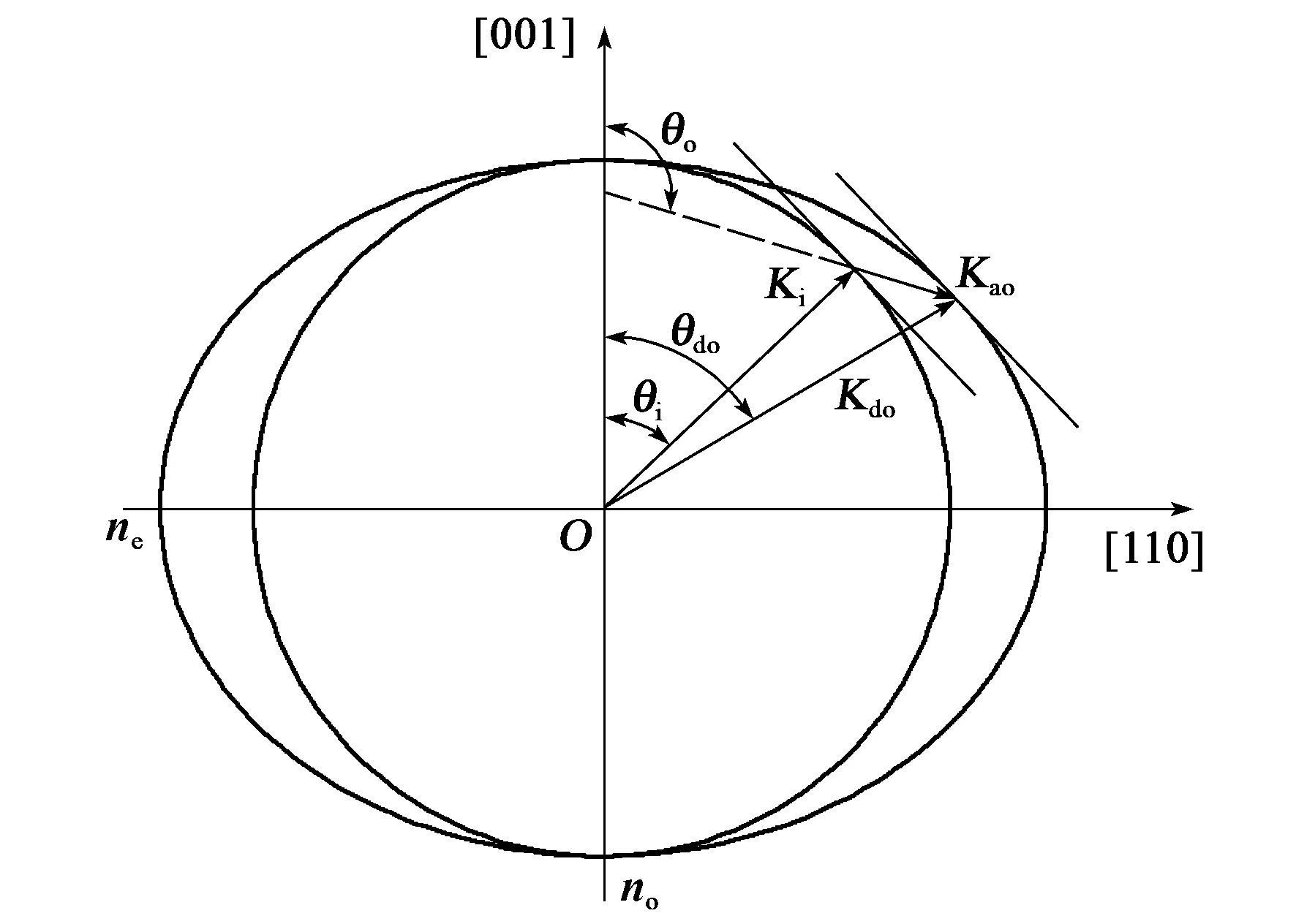
图3 入射光为o光时的波矢量布局

Kdo=Ki+Kao

(2)

由图2、3可见,两种滤光模式的波矢量布局差别较大。对于入射光为e光的滤光器,其入射光折射率曲面是以长短轴分别为ne、no的椭圆,衍射光折射率曲面是半径为no的圆,且θi>θde;入射光为o光的滤光器,其入射光折射率曲面是半径为no的圆,衍射光是以长短轴分别为ne、no的椭圆,且θi<θdo。

由图1可见,入射e、o光经过滤光器滤光后,得到的衍射光分别为衍射o、e光,衍射o光和衍射e光空间分离。滤光器工作示意图如图4所示。入射e光在可见光波段工作,经过滤光器后得到衍射o光,进入可见光探测器。入射o光在中波波段工作,经过滤光器后得到衍射e光,进入中波探测器,两个探测器相互独立,不相互干扰。

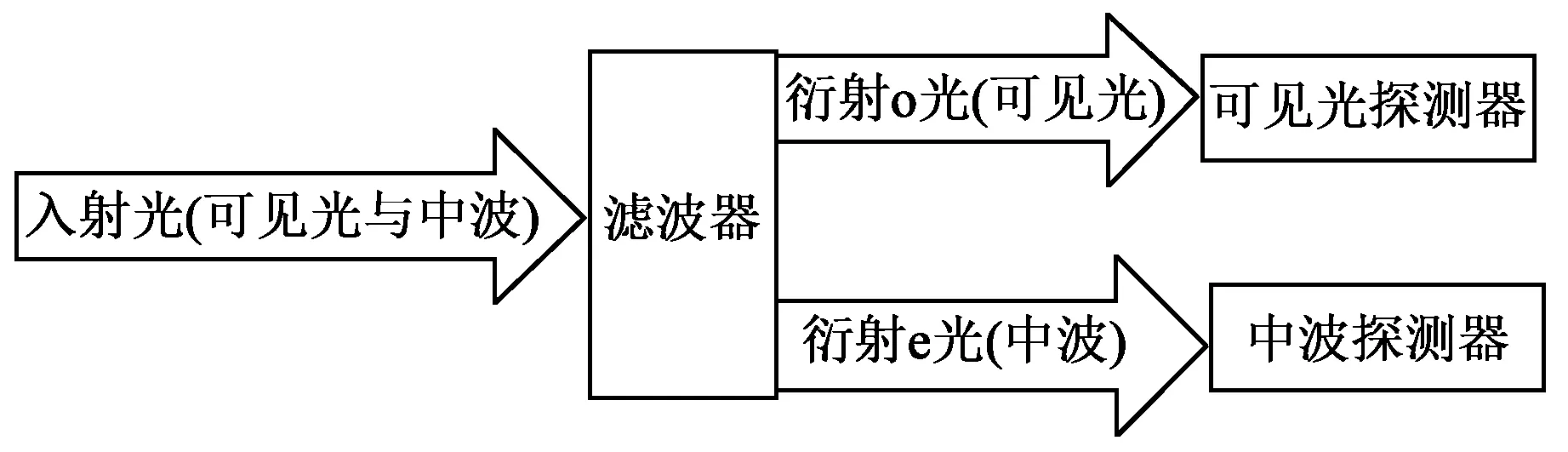
图4 滤光器工作示意图

1.2 光波长调谐关系

1.2.1 可见光波段

入射光e光在可见光波段工作,得到衍射光o光。根据非同向滤光器“切面平行动量匹配条件”理论[4],入射光折射率ni为

(3)

衍射o光在晶体内的衍射光极角θde为

(4)

入射极角为θi时,入射光e光获得大孔径角需要的最佳超声极角θe为

(5)

滤出的可见光光波长λe为

(6)

式中:ve为在超声极角θe时氧化碲晶体的超声波速度;fe为可见光波段的工作频率。

式(6)是可见光波段的光波长调谐关系,根据式(6)可求出λe(入射e光)对应的工作频率fe,或工作频率fe对应的光波长λe。

1.2.2 中波波段

中波波段工作入射光取o光,得到的衍射光为e光。根据非同向滤光器“切面平行动量匹配条件”理论[3],衍射e光在晶体内的衍射光极角θdo为

(7)

衍射光的折射率nd为

(8)

入射极角为θi时,入射光o光获得大孔径角需要的最佳超声极角θo为

(9)

滤出的中波光波长λo为

(10)

式中:vo为在超声极角θo时氧化碲晶体的超声波速度;fo为可见光波段的工作频率。

式(10)是中波波段的光波长调谐关系。根据式(10)可求出光波长λo(入射o光)对应的工作频率fo,或工作频率fo对应的光波长λo。

1.3 孔径角

孔径角是表征滤光器性能的一个重要指标,分为水平孔径角和竖直孔径角两种,水平孔径角通常都小于竖直孔径角。因此,实际应用中侧重考察水平孔径角,孔径角越大,滤光器集光能力越强,系统灵敏度越高。

1.3.1 可见光波段

对于可见光波段,其入射光取e光,得到的衍射光为o光。根据e光入射型滤光器的非同向大角孔径理论[2],晶体外的水平孔径角Δθe和竖直孔径角ΔΦe[2]分别为

(11)

(12)

式中Le为可见光波段的声光互作用长度。式(11)与文献[2]的水平孔径角相差2倍,其原因是文献[2]只考虑了相位失配0.45的情况,式(11)按照相位失配±0.45计算,故式(11)更符合滤光器的实际测量结果。

1.3.2 中波波段

对于中波波段,其入射光取o光,得到的衍射光为e光。根据o光入射型滤光器的非同向大角孔径理论[3],晶体外的水平方向孔径角Δθo为

(13)

(14)

式中Lo为中波波段的声光互作用长度。

晶体外的竖直方向孔径角ΔΦo为

(15)

1.4 光谱分辨率

1.4.1 可见光波段

对于可见光波段,其入射光取e光,得到的衍射光为o光。根据e光入射型滤光器的非同向大角孔径理论[2],入射e光的光谱分辨率Δλe为

(16)

式中b为氧化碲晶体的色散常数。

1.4.2 中波波段

根据o光入射型滤光器的非同向大角孔径理论[3],入射o光的光谱分辨率Δλo为

(17)

由式(16)、(17)可见,对于相同的入射极角θi,在光波长和互作用长度等参数相同的条件下,由于o光入射型滤光器的θd>θi(见图3),所以对于相同的入射极角θi,入射o光能得到更小的光谱分辨率,即o光入射型滤光器可获得比e光入射型滤光器更高的光谱分辨率。基于这个原理,在设计双波段滤光器时,把中红外波段设计成o光入射,可见光波段设计成e光入射,即可以较小的声光互作用长度获得更高的光谱分辨率。

2 实验结果分析

按照图1的原理制作出有效光孔径为∅20 mm×20 mm的双波段大孔径角声光可调滤光器,如图5所示。其主要设计参数:取入射极角θi=20°,可见光波段的超声极角θe=98.55°,中波波段的超声极角θo=99.65°,可见波段互作用长度Le=3 mm,中波波段互作用长度Lo=23.1 mm。

图5 滤光器器件外形

如图1所示,在通声面1上制作高频换能器,它吸收高频段射频信号(RF1)产生超声波Kae,超声波Kae与入射光发生声光互作用滤出可见光;在通声面2上制作低频换能器,它吸收低频段射频信号(RF2)产生超声波Kao,超声波Kao与入射光发生声光互作用滤出中波。

2.1 光透过率

滤光器同时工作在可见光与中红外两个波段,因此需要镀制同时兼顾可见光与中红外两个波段的光学增透膜。其工作波长范围较宽,因此在器件通光面上镀制了多达12层宽带减反射膜。用分光光度计测量滤光器光透过率,如表1所示。

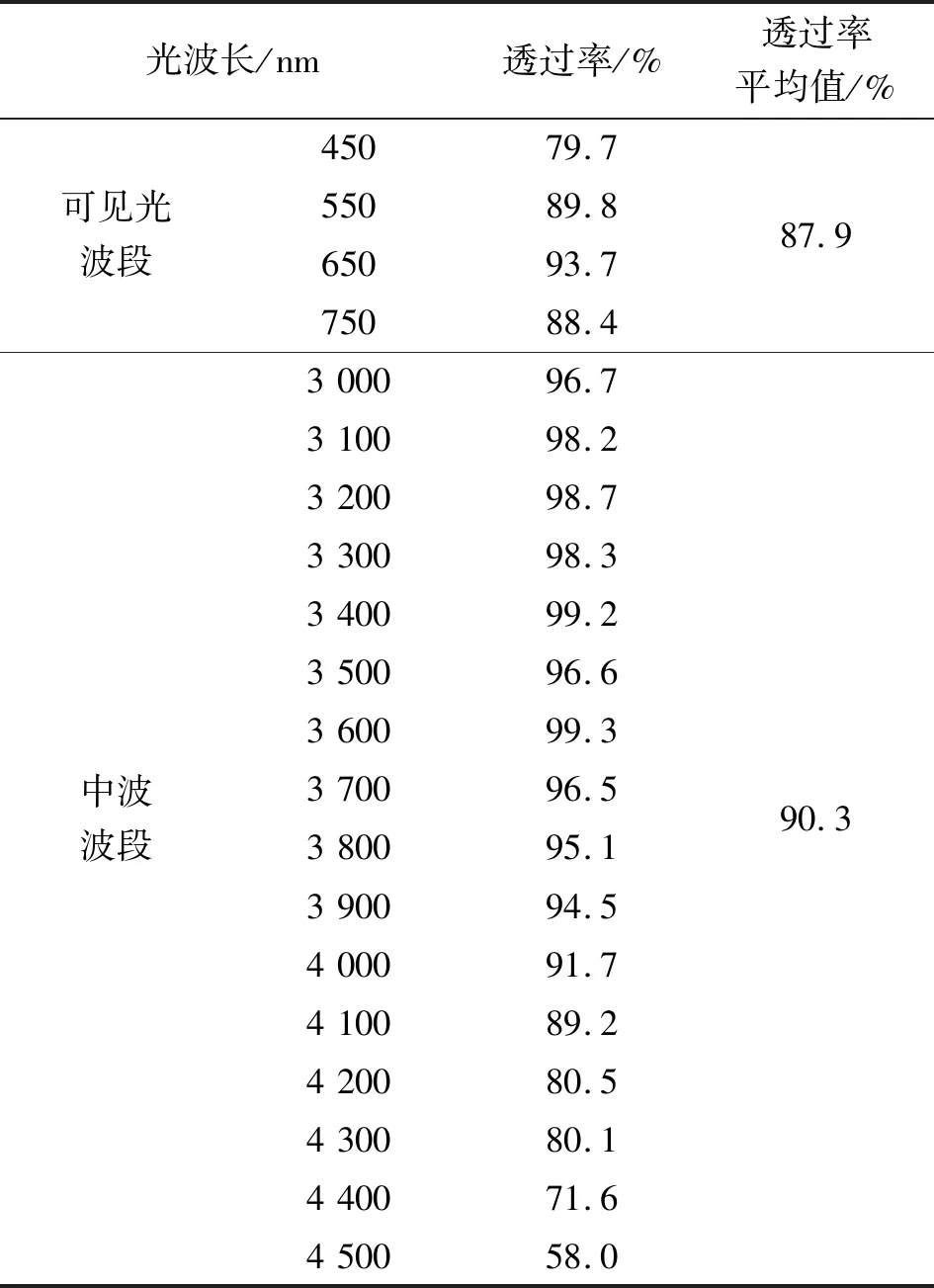
表1 光透过率

制作滤光器的声光介质材料是氧化碲晶体,其透光区为 0.35～5.00 μm,在0.45～4.00 μm内透明,但从4 μm开始光吸收系数逐渐增加,光透过率呈下降趋势。因此,镀膜后滤光器的透过率从光波长4 000 nm开始降低。

2.2 光波长与光谱分辨率

滤光器可见光波段使用的驱动功率约4 W,中波波段使用的驱动功率约11 W,全光谱范围衍射效率达60%。滤光器在紫外波长450 nm时衍射效率较低,其原因是工作频率较高,声波衰减较大[5]。使用专用的两套声光可调滤光器测试系统分别测量了滤光器可见光与中波的工作频率、衍射效率和光谱分辨率,如表2所示。由表可知,光谱分辨率与理论值吻合。

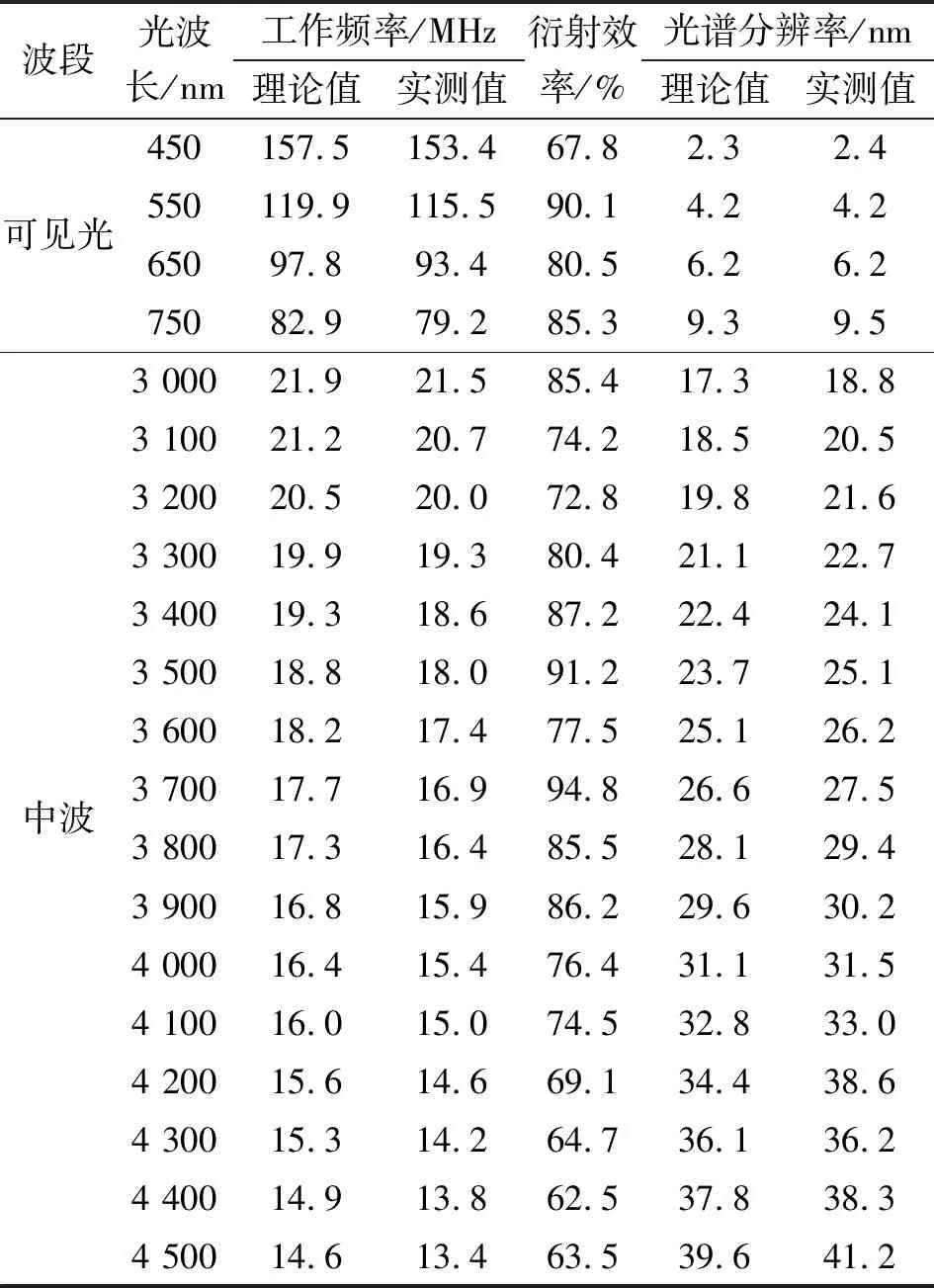
表2 滤光器的光波长、工作频率、衍射效率和光谱分辨率

2.3 孔径角

孔径角测试框图如图6所示。使用632.8 nm激光器测试可见光波段,使用3 200 nm激光器测试中波波段。测试时,激光垂直射入器件入射面,调整驱动频率使衍射效率达到最大,测出此时的衍射光强度I。顺时针旋转器件的角度,当衍射光强度降低为I/2(相当于相位失配0.45)时记录机械式分度台的角度θ1;反时针旋转器件的角度,当衍射光强度再次降低为I/2(相当于相位失配-0.45)时记录机械式分度台的角度θ2,则器件孔径角θ=|θ1-θ2|,则测出的孔径角相当于相位失配±0.45。

图6 孔径角测试框图

孔径角测试结果如表3所示。可见光与中波两个波段都同时获得了大于6°的孔径角。考虑到工艺制作误差与测量误差,可见光与中波两个波段的孔径角与理论值相吻合。

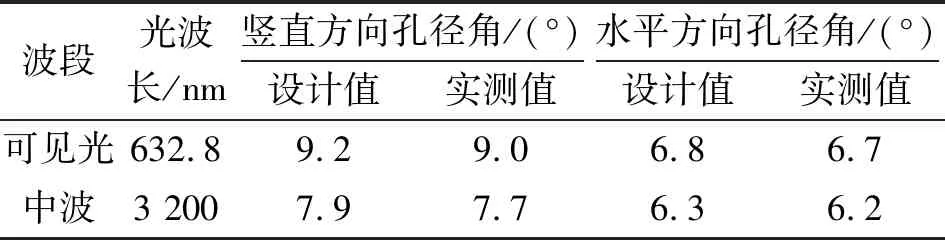
表3 滤光器孔径角测试结果

3 结束语

测试结果与理论值基本吻合,高频段滤出了可见光(450～750 nm),低频段滤出了中波(3 000～4 500 nm),并且可见光与中波两个波段同时获得了大孔径角滤光,因此,在一个滤光器上实现了同时兼顾可见光与中波波段的功能。

把可见光与中波两个波段集成在一个滤光器上的工作模式是声光光谱滤光中的一大创新,为同时快速获取目标的可见光与中波光谱图像创造了条件,在充分挖掘生物细胞组织的光谱特征信息、深入识别生物组织的结构特征、观察病灶多光谱变化趋势、精准给出诊断结果方面具有重要的意义。